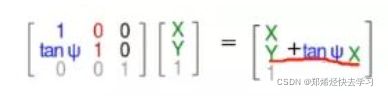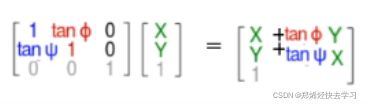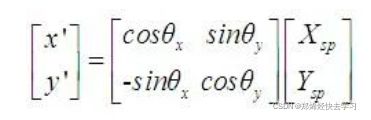OpenCv入门(二)——仿射变换和透视变换
为什么要图像重映射?我们可以把每个像素的位置重新映射到新的位置,这可用来创建图像特效,或者修正因镜片等原因导致的图像扭曲。
如何实现?使用OpenCv的remap函数,首先需要定义在重映射处理中使用的映射参数,然后把映射参数应用到输入图像。很明显,定义映射参数的方式将决定产生的效果。这里定义一个转换函数,在图像上创建波浪形效果:
// 重映射图像,创建波浪形效果
void wave(const cv::Mat &image, cv::Mat &result) {
// 映射参数
cv::Mat srcX(image.rows,image.cols,CV_32F);
cv::Mat srcY(image.rows,image.cols,CV_32F);
// 创建映射参数
for (int i=0; i(i,j)= j; // 保持在同一列
// 原来在第 i 行的像素,现在根据一个正弦曲线移动
srcY.at(i,j)= i+5*sin(j/10.0);
}
}
// 应用映射参数
cv::remap(image, // 源图像
result, // 目标图像
srcX, // x 映射
srcY, // y 映射
cv::INTER_LINEAR); // 填补方法
} 程序实现原理:
重映射是通过修改像素的位置,生成一个新版本的图像,为了构建新图像,需要指定目标图像中每个像素的原始位置。我们需要的映射函数应该能根据像素的新位置得到像素的原始 位置。这个转换过程描述了如何把新图像的像素映射回原始图像,因此称为反向映射。
在opencv中可以用两个映射参数来说明反向映射参数来说明反向映射:一个针对x坐标,一个针对y坐标,它们都使用浮点数型的cv::Mat实例来表示:
// 映射参数
cv::Mat srcX(image.rows,image.cols,CV_32F); // x 方向
cv::Mat srcY(image.rows,image.cols,CV_32F); // y 方向这些矩阵大小决定了目标图像的大小。用下面的代码可以从原始图像获得目标图像中(i,j)像素的值:
( srcX.at(i,j) , srcY.at(i,j) ) 对于水平翻转,可以改变左右两边的坐标值,也可以实现:
// 创建映射参数
for (int i=0; i(i,j)= image.cols-j-1;
srcY.at(i,j)= i;
}
} 要实现效果只需要调用remap函数:
// 应用映射参数
cv::remap( image, // 源图像
result, // 目标图像
srcX, // x 方向映射
srcY, // y 方向映射
cv::INTER_LINEAR); // 插值法(1)使用图像实现逆透视(鸟瞰图)
参考博客:逆透视变换(IPM)多种方式及代码总结 - 古月居
在自动/辅助驾驶中,车道线的检测非常重要。要在前视摄像头拍摄的图像中,由于透视效应的存在,本来平行的事物,在图像中确实相交的。而IPM变换就是消除这种透视的效应,所以也叫逆透视。
IPM分为三种:透视变换、仿射变换、单应性变换。
-
透视变换:不能保证物体形状的"平行性"。透视变换是将一个平面投射到另一个平面,就是把一张图片投射到另一张图片,求的是同一张图片到它的投影图片之间的变换。
-
仿射变换:透视变换的特殊形式。保证物体形状的”平值性“和”平行性",一般为平移旋转等操作。
-
单应性变换:由三维空间拍摄两张不同的图片来获取关键点,求的是该图片到另一个角度图片的变换,但是变换过后还是这张图片,没有变成另一个角度的图片,变换过后和另一张图片还是不同,因为三维空间得到的背景不同,所以变换后并不能获取关键点对的另一张图片。
IPM变换方法:
-
输入:至少四个对应点对,不能有三点及其以上共线,不需要知道摄像机参数或者平面位置的任何信息。
-
数学原理:利用点对,求解逆透视变换矩,其中map_matrix是一个3×3矩阵,所以可以构建一个线性方程组进行求解。其实就是我们上面说的类似于卷积的操作了。如果大于4个点,可采用ransc的方法进行求解,一边具有更好的稳定性。
-
选点方法:一般采取手动选取,或者利用消影点(图像上平行线的交点,也叫消失点,vanish point)选取。
实现目标及其实现代码:
从拍照视角变成鸟瞰图,是自动驾驶领域和机器人导航种常用的手段,以便在该平面上进行规划和导航。这种变换常常用到透视变换,但我们今天在讲解透视变换时,需要普及一下其他的变换,包括平移、旋转、错切以及仿射变换。
基础的变换有如下:
-
平移
对于矩阵的平移怎么做?对每一个像素点坐标进行平移,就是在相应的矩阵上x,y都加一个变量。
-
放缩
就是将矩阵图像放缩n倍,也就是长宽各乘一个变量。
-
旋转
对矩阵(图片)进行旋转,关于旋转的数学推导在后边的仿射会介绍:
-
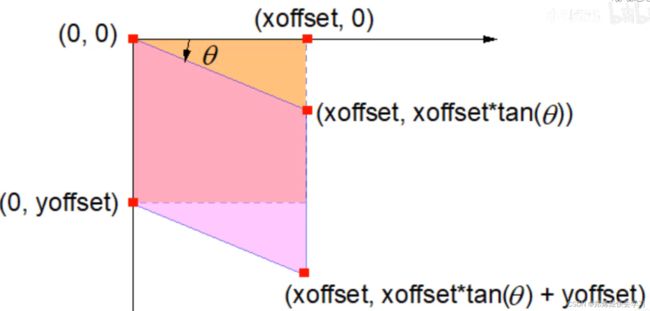
错切
关于y方向的错切:
相应的数学表达:
关于x轴方向的错切:
那么相应的数学表达:
之后把其两者合起来:
那么我们就可以实现如下的四种变换:
那么等式右边就是仿射变换矩阵,是由原图像进行平移、旋转、放缩、错切之后得来的。
那么我们的仿射变换跟透视变换到底有什么区别?
仿射变换是可以将矩形变换成平行四边形(即变换后各边依旧平行),而透视变换可以变成任意不规则四边形。所以仿射变换是透视变换的子集。
仿射变换其实就是单纯对图片进行缩放,倾斜和旋转,因此图片不论如何变换,线之间的平行性是不变的。而透视变换,则是当观察者的视角发生变化时物体发生透视变换,此变换允许造成透视形变。
那么如何实现?
(2)仿射变换
opencv中给出了仿射变换的函数接口:
warpAffine(
InputArray src, //输入图像
OutputArray dst, //输出图像
InputArray M, //仿射计算矩阵
Size dsize, //输出图像大小
int flags = INIET_LINEAR, //插值方法
int borderMode = BORDER_CONSTANT,
const Scalar& borderValue = Scalar()
)这函数的前两个函数就不用详细说了,那么第三个矩阵m是什么,第三个参数其实就是要我们输入上方的2*3的仿射计算矩阵:
这个东西可以去掉最后一行。
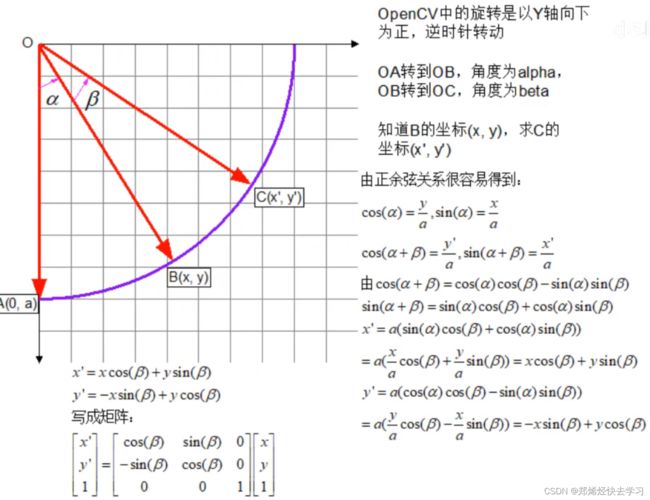
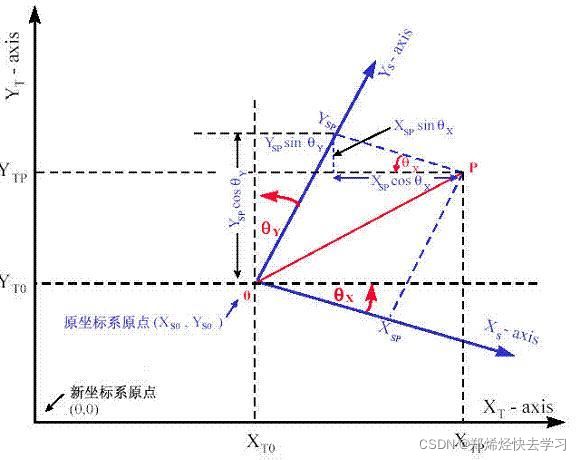
这个函数的推导在上面,就不多叙述了。这里的核心思想是:坐标系中某个点的旋转可以等价地去旋转坐标轴。
再用这张图看看:
我们需要将原坐标系原点(Xs0,Ys0)旋转至新坐标原点。然后要完成旋转操作,旋转操作是基于原点的,也就是图中的蓝色坐标。
我们如何把那点P转移到我们需要的坐标轴上?并且在新建的坐标上确定我们的坐标位置?
那就是一系列的几何知识了:
基于数学,我们可以通过简单的立体几何知识确定P在新坐标系中的坐标。P在新坐标中的X坐标和Y坐标分别是:
那么由矩阵来表示就是这样:
那么我们完成了旋转操作,那么接下来的平移:
那么这个矩阵就出来了。
那么推导是这样的,那怎么去实现?opencv提供了计算仿射矩阵的函数接口:
getAffineTransform(
const Point2f* src, //输入图像的点集
const Point2f* dst //输出图像的点集
)
我们需要输入三对点集。也就是上面的矩阵,要有六个变量,因此至少需要列六个等式才可以算出该矩阵。我们需要找输入图像和输出图像上一一对应的三对点(3个x,y对应计算式)来作为输入。
(3)透视变换原理
仿射变换是在二维空间中的旋转,平移和缩放。而透视变换则是在三维空间中视角的变化。
opencv给的透视变换的函数接口:
void warPerspective(
InputArray src, //输入图像
OutputArray dst, //输出图像
InputArray M, //输入透视变换矩阵M
Size dsize,
int flags = INTER_LINEAR,
int borderMode=BORDER_CONSTANT,
const Scalar& borderValue=Scalar()
);和仿射变换基本相同,不同的是输入透视变换矩阵M大小为3*3:
上面的矩阵的未知量比仿射变换的矩阵多了一个透视变换矩阵T3(两个未知量),因此我们一共有八个未知量,所以需要给下面的透视变换矩阵的函数提供四对以上的点来求解:
Mat cv::getPerspectiveTransform (
const Point2f src[], //输入图像点集
const Point2f dst[], //输出图像点集
);T1为线性变换完成旋转,错切和放缩,T2完成平移操作。T3就是设了两个变量来表示映射关系。
取原图上的四点,之后计算该四点变换后的位置。就是把那个像梯形的东西,转换为长方形。
代码如下:
//逆透视
cv::Mat road = cv::imread("./image/cross.jpg");
cv::imshow("原来", road);
//存放要更改的图片
cv::Mat dstImage(1500, 1500, CV_16F);
cv::Point2f imPts[4], objPts[4], mypoint[4];
//画原来的点
mypoint[0].x = 166; mypoint[0].y = 195;
mypoint[1].x = 482; mypoint[1].y = 195;
mypoint[2].x = 80; mypoint[2].y = 350;
mypoint[3].x = 568; mypoint[3].y = 350;
//你想要变成的点
objPts[0].x = 500; objPts[0].y = 200;
objPts[1].x = 1000; objPts[1].y = 200;
objPts[2].x = 500; objPts[2].y = 0;
objPts[3].x = 1000; objPts[3].y = 0;
//计算透视变换矩阵
cv::Mat H = cv::getPerspectiveTransform(mypoint, objPts);
//进行透视变换
cv::warpPerspective(road, dstImage, H, dstImage.size());
//画出透视变换后的四个点
circle(dstImage, objPts[0], 9, cv::Scalar(0, 0, 255), 3);
circle(dstImage, objPts[1], 9, cv::Scalar(0, 0, 255), 3);
circle(dstImage, objPts[2], 9, cv::Scalar(0, 0, 255), 3);
circle(dstImage, objPts[3], 9, cv::Scalar(0, 0, 255), 3);
cv::namedWindow("dddd", cv::WINDOW_FREERATIO);
cv::imshow("dddd", dstImage);
0x04 直方图统计像素
在单通道灰度图像种,每个像素都有一共0(黑色)~255(白色)的整数。对于每个灰度,都有不同数量的像素分布在图像内,具体取决于图片内容。
-
直方图是一个简单的表格,表示一幅图像(优势是一组图像)中具有某个值的像素的数量。所以直方图一共有256个项目,也叫箱子(bin)。
实现:
指定一个专门用于处理单通道的类:
class HistogramID {
private:
int histSize[1]; //直方图中箱子的数量
float hranges[2]; //值范围
const float* ranges[1]; //值范围的指针
int channels[1]; //要检查的通道数量
public:
HistogramID()
{
//准备一维直方图的默认参数
histSize[0] = 256; //个数
hranges[0] = 0.0; //min
hranges[1] = 256.0; //max
ranges[0] = hranges; //指向它
channels[0] = 0; //先关注通道0
}
};计算灰度直方图:
//计算灰度直方图
cv::Mat HistogramID::getHistogram(const cv::Mat& image) {
cv::Mat hist;
//使用calcHist函数计算一维直方图
cv::calcHist(&image, 1, //仅为一幅图像的直方图
channels, //使用的通道
cv::Mat(), //不使用掩码
hist, //作为结果的直方图
1, //这是一维的直方图
histSize, //箱子数量
ranges //像素值的范围
);
return hist;
}使用:
//计算灰度直方图
HistogramID VV;
cv::Mat histo = VV.getHistogram(image);
//遍历数组,可得到对应的灰度的个数
for (int i = 0; i < 256; i++)
std::cout << "Value" << i << "=" << histo.at(i) << std::endl; 可能这么看不大直观,可以使用画图画出来:
//创建一个表示直方图的图像
cv::Mat getImageOfHistogram(const cv::Mat& hist, int zoom)
{
//取得箱子值的最大值和最小值
double maxVal = 0;
double minVal = 0;
cv::minMaxLoc(hist, &minVal, &maxVal, 0, 0);
//取值直方图
int histSize = hist.rows;
//用于显示直方图的方形图像
cv::Mat histImg(histSize * zoom,histSize * zoom, CV_8U, cv::Scalar(255));
//设置最高点为100%的箱子个数
int hpt = static_cast(1.00 * histSize);
//为每个箱子画垂直线
for (int h = 0; h < histSize; h++)
{
float binVal = hist.at(h);
if (binVal > 0)
{
int intensity = static_cast(binVal * hpt / maxVal);
cv::line(histImg, cv::Point(h * zoom, histSize * zoom),
cv::Point(h * zoom, (histSize - intensity) * zoom),
cv::Scalar(0), zoom);
}
}
return histImg;
}
//画出直方图
cv::Mat HistogramID::getHistogramImage(const cv::Mat& image,int zoom) {
//计算出直方图
cv::Mat hist =getHistogram(image);
//创建图像
return getImageOfHistogram(hist,zoom);
} 使用:
//以图像形式显示直方图
cv::namedWindow("Histogram");
cv::imshow("Histogram",VV.getHistogramImage(image));从上面图形化的直方图可以看出,在黑白两种颜色都有一个很大的尖峰,这两部分像素也分别对应了图像的背景和前景。所以在这两部分之间的那个值其实就是我们需要的阈值。我们取直方图中在升高为顶峰之前的最小值的位置(灰度值为100)对其进行阈值处理,可得到二值化图像:
//输出二值化图像
cv::Mat thresholded;
cv::threshold(
image,
thresholded,
100,
255,
cv::THRESH_BINARY //阈值化类型
);
cv::imshow("thresholded", thresholded);但是可以发现,这种方法算出来的二值化图像,实在是太多噪点了: