计算机视觉（二）特征提取与匹配

一、Harris角点检测

1.1 基本思想

HARRIS角点检测，就是从图像局部的小窗口观察图像特征，在某点划个n*n大小的窗口，让它在各个方向上移动，如果每个点都会导致灰度值有较大的变化，那么这个点就是角点。数学表达式为：

对I(x+u,y+v)进行二维泰勒级数展开，取一阶近似，最后变为求解矩阵：

根据矩阵M的特征值可以知道这个点是否是角点。

在不需要实际计算特征值的情况下，为了把重要的情况和其他情况分开，Harris和Stephens在文献中引入了指示函数R：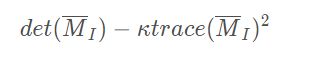
其中，


最终用下面这张图判断图像的角点

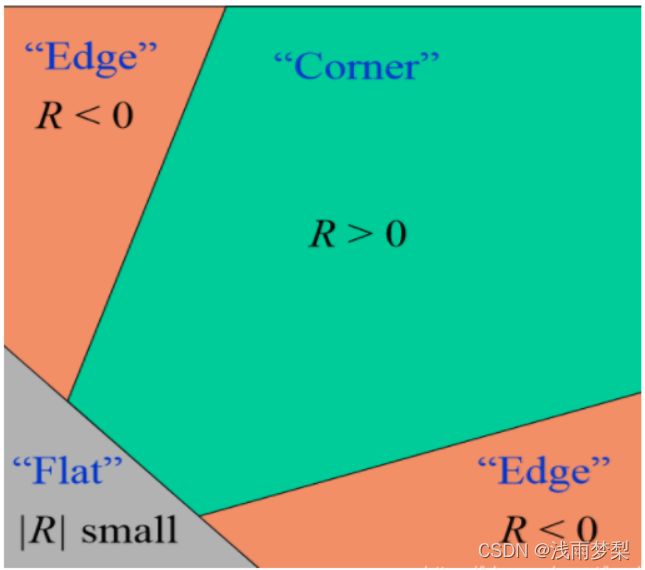
1.2 代码实现

算法流程：
1.将图像转为灰度图像
2.利用Sobel滤波器求出 海森矩阵 (Hessian matrix)


3.将高斯滤波器分别作用于Ix²、Iy²、IxIy；
4.计算每个像素的 R= det(H) - k(trace(H))²。det(H)表示矩阵H的行列式，trace表示矩阵H的迹。通常k的取值范围为[0.04,0.16]。
5.满足 R>=max® * th 的像素点即为角点。th常取0.1。

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt


# Harris corner detection
def Harris_corner(img):
    ## Grayscale
    def BGR2GRAY(img):
        gray=cv.cvtColor(img,cv.COLOR_BGR2GRAY)
        gray = gray.astype(np.uint8)
        return gray

    ## Sobel
    def Sobel_filtering(gray):
        # get shape
        H, W = gray.shape

        # sobel kernel
        sobely = np.array(((1, 2, 1),
                           (0, 0, 0),
                           (-1, -2, -1)), dtype=np.float32)

        sobelx = np.array(((1, 0, -1),
                           (2, 0, -2),
                           (1, 0, -1)), dtype=np.float32)

        # padding
        tmp = np.pad(gray, (1, 1), 'edge')

        # prepare
        Ix = np.zeros_like(gray, dtype=np.float32)
        Iy = np.zeros_like(gray, dtype=np.float32)

        # get differential
        for y in range(H):
            for x in range(W):
                Ix[y, x] = np.mean(tmp[y: y + 3, x: x + 3] * sobelx)
                Iy[y, x] = np.mean(tmp[y: y + 3, x: x + 3] * sobely)

        Ix2 = Ix ** 2
        Iy2 = Iy ** 2
        Ixy = Ix * Iy

        return Ix2, Iy2, Ixy

    # gaussian filtering
    def gaussian_filtering(I, K_size=3, sigma=3):
        # get shape
        H, W = I.shape

        ## gaussian
        I_t = np.pad(I, (K_size // 2, K_size // 2), 'edge')

        # gaussian kernel
        K = np.zeros((K_size, K_size), dtype=np.float)
        for x in range(K_size):
            for y in range(K_size):
                _x = x - K_size // 2
                _y = y - K_size // 2
                K[y, x] = np.exp(-(_x ** 2 + _y ** 2) / (2 * (sigma ** 2)))
        K /= (sigma * np.sqrt(2 * np.pi))
        K /= K.sum()

        # filtering
        for y in range(H):
            for x in range(W):
                I[y, x] = np.sum(I_t[y: y + K_size, x: x + K_size] * K)

        return I

    # corner detect
    def corner_detect(gray, Ix2, Iy2, Ixy, k=0.04, th=0.1):
        # prepare output image
        out = np.array((gray, gray, gray))
        out = np.transpose(out, (1, 2, 0))

        # get R
        R = (Ix2 * Iy2 - Ixy ** 2) - k * ((Ix2 + Iy2) ** 2)

        # detect corner
        out[R >= np.max(R) * th] = [255, 0, 0]

        out = out.astype(np.uint8)

        return out

    # 1. grayscale
    gray = BGR2GRAY(img)

    # 2. get difference image
    Ix2, Iy2, Ixy = Sobel_filtering(gray)

    # 3. gaussian filtering
    Ix2 = gaussian_filtering(Ix2, K_size=3, sigma=3)
    Iy2 = gaussian_filtering(Iy2, K_size=3, sigma=3)
    Ixy = gaussian_filtering(Ixy, K_size=3, sigma=3)

    # 4. corner detect
    out = corner_detect(gray, Ix2, Iy2, Ixy)

    return out


# Read image
img = cv.imread("E:/CV/images/6.jpg")
img = cv.resize(img, (800, 600), interpolation=cv.INTER_CUBIC)
img.astype(np.float32)
# Harris corner detection
out = Harris_corner(img)
cv.imshow("result", out)
cv.waitKey(0)
cv.destroyAllWindows()

运行结果如下：

二、SIFT(尺度不变特征变换)

2.1 基本思想

SIFT特征不只具有尺度不变性，即使改变旋转角度，图像亮度或拍摄视角，仍然能够得到好的检测效果。

SIFT特征检测主要有四个步骤：

1、尺度空间的极值检测
2、特征点定位
3、特征方向赋值
4、特征点描述
关于尺度空间：
在早期图像的多尺度通常使用图像金字塔表示形式。图像金字塔是同一图像在不同的分辨率下得到的一组结果，其生成过程一般包括两个步骤：
1、对原始图像进行平滑
2、对处理后的图像进行降采样
高斯尺度空间：

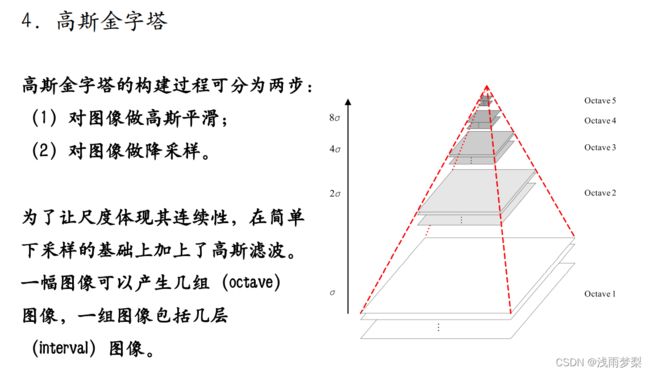
一副图像其高斯尺度空间可由其和不同的高斯卷积得到：
L ( x , y , σ ) = G ( x , y , σ ) ∗ I ( x , y ) \ L(x,y,σ)=G(x,y,σ)∗I(x,y)
其中， G ( x , y , σ ) \ G(x,y,σ) G(x,y,σ) 是高斯核函数
构建尺度空间的目的是为了检测出在不同的尺度下都存在的特征点，而检测特征点较好的算子是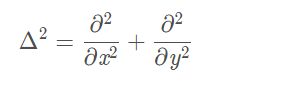

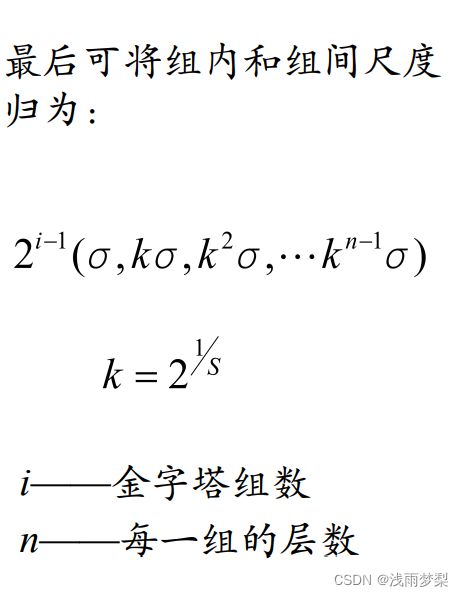
使用LoG虽然能较好的检测到图像中的特征点，但是其运算量过大，通常可使用DoG（差分高斯，Difference of Gaussina）来近似计算LoG[Marr and Hidreth]。
DoG

设k为相邻两个高斯尺度空间的比例因子，则DoG的定义：

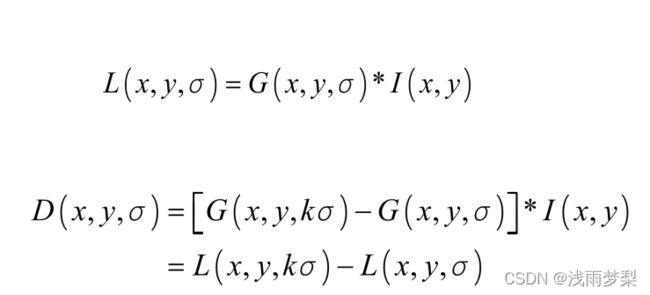
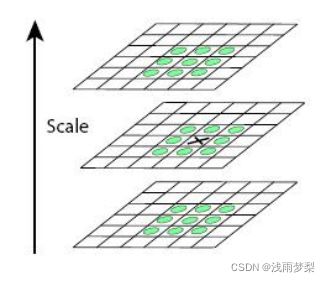
为了寻找尺度空间的极值点，每个像素点要和其图像域（同一尺度空间）和尺度域（相邻的尺度空间）的所有相邻点进行比较，当其大于（或者小于）所有相邻点时，改点就是极值点。如图所示，中间的检测点要和其所在图像的3×3邻域8个像素点，以及其相邻的上下两层的3×3领域18个像素点，共26个像素点进行比较。
从上面的描述中可以知道，每组图像的第一层和最后一层是无法进行比较取得极值的。为了满足尺度变换的连续性，在每一组图像的顶层继续使用高斯模糊生成3幅图像，高斯金字塔每组有S+3层图像，DoG金字塔的每组有S+2组图像。

找到了特征点之后，我们还要删除不好的特征点

通过比较检测得到的DoG的局部极值点实在离散的空间搜索得到的，由于离散空间是对连续空间采样得到的结果，因此在离散空间找到的极值点不一定是真正意义上的极值点，因此要设法将不满足条件的点剔除掉。可以通过尺度空间DoG函数进行曲线拟合寻找极值点，这一步的本质是去掉DoG局部曲率非常不对称的点。
要剔除掉的不符合要求的点主要有两种：
1.低对比度的特征点
2.不稳定的边缘响应点
在删除不好的特征点之后，要进行关键点方向匹配

确定关键点的方向采用梯度直方图统计法，统计以关键点为原点，一定区域内的图像像素点对关键点方向生成所作的贡献。
为了增强匹配的鲁棒性，可以将方向分为主方向与辅方向，

关键点描述
特征描述符的生成大致有三个步骤：
1.校正旋转主方向，确保旋转不变性。
2.生成描述子，最终形成一个128维的特征向量
3.归一化处理，将特征向量长度进行归一化处理，进一步去除光照的影响。
为了保证特征矢量的旋转不变性，要以特征点为中心，在附近邻域内将坐标轴旋转θ（特征点的主方向）角度，即将坐标轴旋转为特征点的主方向。旋转后邻域内像素的新坐标为：


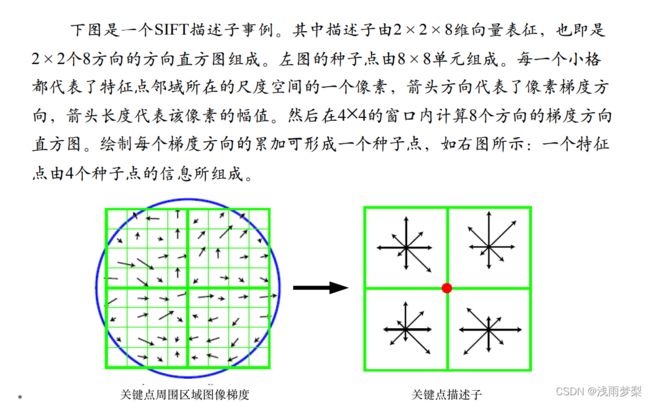
对每个关键点使用4×4共16个种子点来描述，这样一个关键点就可以产生128维的SIFT特征向量。

2.2 代码实现

import numpy as np
import cv2
from matplotlib import pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

img1 = cv2.imread(
    "E:/CV/images/11.jpg")  # 导入灰度图像
img2 = cv2.imread(
    "E:/CV/images/12.jpg")
img1=cv2.cvtColor(img1,cv2.COLOR_BGRA2RGB)
img2=cv2.cvtColor(img2,cv2.COLOR_BGRA2RGB)

detector = cv2.ORB_create()  # Oriented FAST and Rotated BRIEF

# detector = cv2.AKAZE_create()

kp1 = detector.detect(img1, None)
kp2 = detector.detect(img2, None)
kp1, des1 = detector.compute(img1, kp1) # keypoint 是关键点的列表,desc 检测到的特征的局部图的列表
kp2, des2 = detector.compute(img2, kp2)
# 获得一个暴力匹配器的对象
bf = cv2.BFMatcher(cv2.NORM_HAMMING, crossCheck=True)


# 利用匹配器 匹配两个描述符的相近程度
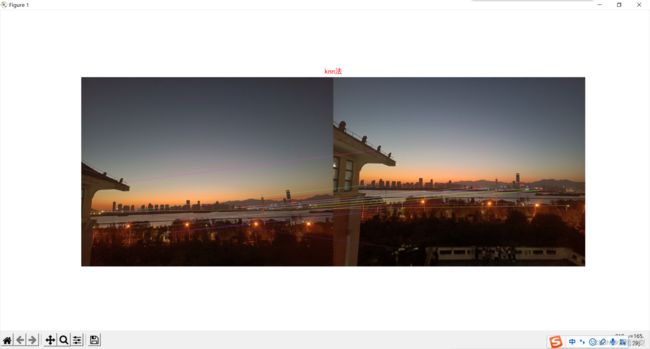
"""knn法"""
matches = bf.knnMatch(des1, des2, k=1)  # knn 匹配可以返回k个最佳的匹配项、bf返回所有的匹配项
img32 = cv2.drawMatchesKnn(img1, kp1, img2, kp2, matches[: 50], img2, flags=2)

plt.figure(figsize=(10,10))
plt.title('knn法',fontsize=12,color='r')
plt.imshow(img32)
plt.axis('off')
plt.show()

cv2.waitKey(0)
cv2.destroyAllWindows()

运行结果如下：

细看还是有一定错误的