AI上推荐 之 多任务loss优化(自适应权重篇)

1. 写在前面

在多任务学习中，往往会将多个相关的任务放在一起来学习。例如在推荐系统中，排序模型同时预估候选的点击率和浏览时间。相对于单任务学习，多任务学习有以下优势：

• 多个任务共享一个模型，占用内存量减少；
• 多个任务一次前向计算得出结果，推理速度增加；
• 关联任务通过共享信息，相互补充，可以提升彼此的表现。

前面的一篇文章，主要是从模型结构的角度聊了下多任务学习，介绍了工业界非常经典也常用的MMOE模型，然而，对于多任务学习， Loss的优化也非常重要， 因为我们知道通过多个目标去指导网络进行统一的训练，这些目标之间有没有冲突？ 多个目标loss之间如何配合？ loss的规模是否一致？ 等等， 所以这篇文章， 通过几篇paper， 来统一梳理下，在多任务模型训练时， 关于多个loss之间优化常用到的相关思路， 当然这些思路不仅适用于推荐， 只要是多个任务，多个loss同时指导模型训练的场景，比如cv里面的全景感知系统(可能需要同时做目标识别，分割，分类)，都可以考虑这些思路方法， 所以这次整理的更像是多任务学习loss优化的一些范式思想。这篇文章会超级长，总结了四篇经典loss优化自适应权重paper的精华内容并通过代码复现和实验进行了对比。 老规矩：根据目录，各取所需即可。

loss就想菲涅尔透镜， 纵使你能设计它的含义， 也未必能设计它的梯度，故暴力一轮，差不多就该躺平了

大纲如下：

• why 多任务学习需要loss优化？
• SharedBottom模型设计思路
• Gradnorm(通过梯度标准化的方式自适应平衡多个任务之间的loss)
• Dynamic Weight Averaging(动态加权平均)
• Dynamic Task Prioritization(动态任务优先级)
• Multi-task learning using uncertainty to weigh losses

Ok, let’s go!

2. Why 多任务学习需要loss优化？

从上一篇MMOE我们就应该能了解到，所谓多任务学习，就是一个模型在多个任务中共享权重，并在一次前向传播的过程中进行多重推断。这样的网络不仅是可扩展的，而且这些网络中的共享特性可以获得更健壮的正则化，从而提高模型的性能。因此，在理想的限制下，我们利用多任务网络可以获取更高的效率以及更高的性能。 拿MMOE中的结构图：

但事实真的是我们想的那么简单吗？ 不是的， 多个任务之间可能会出现冲突的情况，而导致训练无法收敛的情况。 下面我们从loss的角度进行分析：

对于多任务的loss， 我们能想到的最简单的结合方式，就是多个任务的loss直接相加，得到整体的loss，通过这个对网络进行优化：
$$L=\sum _i{L}_i$$
这个loss的设计，我们一眼就能看出不合理的地方，因为每个任务loss的量级，每个任务本身的重要程度可能不一样，这样无脑相加，可能导致多任务学习被某个任务主导(比如量级特别大)，这样其他任务的loss起到的作用微妙，就可能产生对主导任务拟合效果很好，但是其他任务效果变差，也就是我们听到的"跷跷板"现象。

所以下面对loss函数进行简单的调整， 对每个任务loss分配个权重总行了吧：
$$L=\sum _i{w}_i{L}_i$$
相对于loss直接相加的方式，这个loss函数对于每个任务的loss进行加权。这种方式允许我们手动调整每个任务的重要性程度。 这种方式至少有下面两个问题我们可以想到：

1. 这个就想人工做特征工程那样，需要非常高深的经验和对任务的了解程度，才有可能把权重设置好， 并且一旦设置好了权重$w$， 在整个训练周期就定死了
2. 不同任务学习的难易程度不同，就会导致不同任务的收敛速度会不一样，比如A任务快收敛了，B任务仍然没训练好等，此时这种固定权重在训练某阶段可能限制任务的学习

现在应该明白为什么多任务学习中loss的优化很重要了，因为你loss如果设定的不好，权重如果设定的不好，就可能导致"跷跷板"现象， 就可能导致网络无法收敛现象，就可能导致某些任务无法学习现象…

那么， 不同任务的loss有没有更好的加权方式呢？ 《周易》里有句话叫做"穷则变，变则通，通则久"，所以更好的加权方式应是在训练过程中能根据不同任务学习的阶段，学习的难易程度，甚至是学习效果动态来调整的。 即：
$$L=\sum _i{w}_i(t)\ast L_i$$
这样才能让网络在训练过程中，对不同的任务做到自适应。 所以，下面整理的几篇paper， 其核心思想都是从不同任务loss平衡的角度出发，研究如何能在训练过程中动态调整不同任务loss的权重。

3. SharedBottom模型设计思路

由于后面的这些paper里loss的优化思路都想用代码复现下，在统一任务上简单跑跑，所以对于每个思路，我都想简单实验下，所以这里需要先给出模型和任务来。

这里首先是这样， 本来是想从上一篇文章的MMOE模型里面直接把后面这种优化loss的算法加入进去，但是呢？ 对于MMOE来讲， 是引入了多个门控机制，对于每个任务，自己学习专家的组合，这也就是说，可能不同的任务采用了不同的专家组合，这些专家组合的输出又各自过了task_power，对于这种情况， 单独拿后面的经典算法gradnorm来说，我就不知道是否能够使用呀(反正我是没有想好该如何写代码)，原因是gradnorm本质上就是每个task_loss要对共享层的最后一层参数W求梯度，然后根据这个梯度幅值去修改每个loss的权重，但是对于MMOE， 我不知道最后一个共享层是啥，所以我只能是在MMOE基础上重新写一个shared bottom的模型，在这个基础上实现gradnorm。 当然数据集依然是新闻推荐数据(后面打算把所有模型使用的数据统一起来)， 而数据预处理，可以参考MMOE那篇的预处理，是一模一样的。

关于shared bottom，上面也整理过，细节这里就不说了，这里只展示下最终实现的这个模型样子，然后记录下这么设计的初衷：

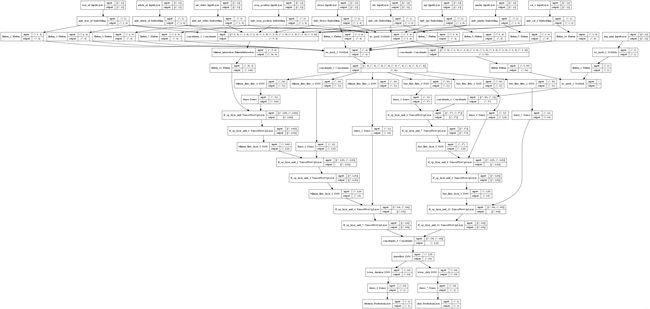
这个模型猛地一看还是挺复杂的，但实际是个"纸老虎"， shared Bottom其实可以非常简单的，底层弄一个DNN作为共享层， 然后再接两个task_tower的DNN，三个DNN即可实现， 具体可以参考deepctr多任务模型。

但我这里底层的特征交互不太想设计的那么简单，因为反正都是花时间嘛， 不如尝试一些其他的东西，比如快手写到的一篇文章里面使用了一个lhuc模块，感觉这个模块设计挺巧妙的，于是乎想整理下这个东西。

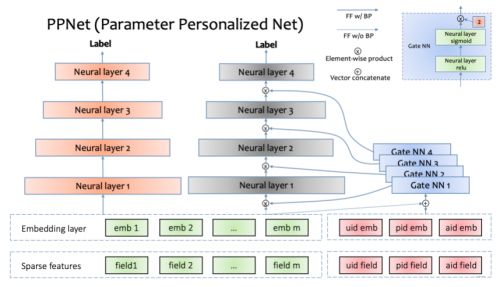
在语音识别领域中，2014年和2016年提出的LHUC算法（learning hidden unit contributions）核心思想是做说话人自适应（speaker adaptation），其中一个关键突破是在DNN网络中，为每个说话人学习一个特定的隐式单位贡献（hidden unit contributions），来提升不同说话人的语音识别效果。

借鉴LHUC的思想，快手推荐团队在精排模型上展开了尝试。经过多次迭代优化，推荐团队设计出一种gating机制，可以增加DNN网络参数个性化并能够让模型快速收敛。快手把这种模型叫做PPNet（Parameter Personalized Net）。据快手介绍，PPNet于2019年全量上线后，显著的提升了模型的CTR目标预估能力。

这个东西，本质上也是类似于一个注意力的东西，只不过加在了DNN的每一层输出向量的每个维度上面。lhuc_net也是类似于一个特征交互式网络， 接收的输入有lhuc_feature，以及其他模块的输出，比如lhuc_feature和原始特征交互，lhuc_feature和FM的输出交互。 我这里把这个模块给实现了下：

def lhuc_net(name, nn_inputs, lhuc_inputs, nn_hidden_units=(128, 64, ), lhuc_units=(32, ), 
             dnn_activation='relu', l2_reg_dnn=0, dnn_dropout=0, dnn_use_bn=False, scale_last=True, seed=2021):
    """这个网络是全连接网络搭建的，主要完成lhuc_feature与其他特征的交互， 算是一个特征交互层，不过交互的方式非常新颖
    
        name: 为当前lhuc_net起的名字
        nn_inputs: 与lhuc_feature进行交互的特征输入，比如fm_out， 或者其他特征的embedding拼接等
        lhuc_inputs: lhuc_net的特征输入，在推荐里面，这个其实是能体现用户个性化的一些特征embedding等
        nn_hidden_units: 普通DNN每一层神经单元个数
        lhuc_units: lhuc_net的神经单元个数
        后面就是激活函数， 正则化以及bn的指定参数，不过多解释
    """
    
    # nn_inputs可以是其他特征的embedding拼接向量，或者是其他网络的输出，比如fM的输出向量等
    cur_layer = nn_inputs       
    
    # 这里的nn_hidden_units是一个列表，里面是全连接每一层神经单元个数
    for idx, nn_dim in enumerate(nn_hidden_units):
        # lhuc_feature走一个塔， 这个塔两层， 最终输出的向量维度和nn_inputs的向量维度保持一致， 每个值在0-1之间，代表权重
        # 表示fm_embedding或者其他特征embdding每个维度上的重要性  
        # 这里其实可以用多层 激活函数用relu 
        lhuc_output = DNN(lhuc_units, dnn_activation, l2_reg_dnn, dnn_dropout, dnn_use_bn, 
                          seed=seed, name="{}_lhuc_{}".format(name, idx))(lhuc_inputs)
        # 最后这里的输出维度要和交互的embedding保持一致， 激活函数是sigmoid，
        lhuc_scale = Dense(int(cur_layer.shape[1]), activation='sigmoid')(lhuc_output)
        
        # 有了权重之后， lhuc_scale与nn_inputs再过一个塔
        cur_layer = DNN((nn_dim, ), dnn_activation, l2_reg_dnn, dnn_dropout, dnn_use_bn, 
                        seed=seed, name="{}_layer_{}".format(name, idx))(cur_layer * lhuc_scale * 2.0)
        
    # 上面这个操作相当于nn_input_embedding过了len(nn_hidden_units)层全连接， 只不过，在过每一层之前，会先lhuc_slot特征通过lhuc_net为
    # nn_input_embedding过完全连接之后的每个维度学习权重，作为每个维度的重要性
    # 如果最后的输出还需要加权，再走一遍上面的操作
    if scale_last:
        lhuc_output = DNN(lhuc_units, dnn_activation, l2_reg_dnn, dnn_dropout, dnn_use_bn, 
                          seed=seed, name="{}_lhuc_{}".format(name, len(nn_hidden_units)))(lhuc_inputs)
        lhuc_scale = Dense(int(cur_layer.shape[1]), activation='sigmoid')(lhuc_output)
        
        cur_layer = cur_layer * lhuc_scale * 2.0
    
    return cur_layer

其实思路比较简单， 前向传播就是原始特征或其他模块的输出特征，再过每一层DNN的时候， 都先有lhuc_feature过gate_DNN得到得到普通DNN当前层的神经元的权重，这样当原始特征过完一层DNN得到输出，就和权重相乘，进行筛选，接下来再过后面的DNN。本质上就是对每一层普通DNN的输出在神经元维度上进行了加权。

有点像Fibinet那里的se模块，不过那个是对每个embedding进行加权筛选，而这里是对DNN输出(可以看成一个embedding)的每个维度进行加权。 也有点像MMOE，只不过那个门控是对专家的输出向量加权， 权重个数等于专家个数。

这个过程中， lhuc_feature以及其他的base_feature选择很重要，这里面涉及特征之间制约性和相关性，我这里结合之前见到的，梳理个我自己的理解:

• lhuc_feature: 主要是用户id， doc_id，doc_类别， doc_字数， doc_作者等embedding拼接， 这些都是用户和item的强烈代表特征， 这个拼接的embedding代表的是用户对于item的兴趣偏好
• base_feature：
  • bias_nn_inputs: 这里一般是原始的特征embedding拼接起来，代表特征的原始信息
  • 其他模块输出，比如fm的输出: 这个是能产生交互的特征embedding，代表的是重要的特征交互信息

所以，lhuc_net主要是在原始信息或者是像fm这种特征交互信息过DNN的每一层之后，会有lhuc_feature对DNN每一层的输出的每个维度，根据用户对于item的兴趣偏好，进行加权，来提升每一层DNN输出的不同维度的贡献程度，来体现用户的个性化信息(相比于不加lhuc_net)，此外，还能进行降维。毕竟通过个性化进行了一波选择。凡是需要过DNN降维的模块输出特征其实都可以加个这样的操作。

所以我感觉这个lhuc_net的思路也是⾮常不错的， 相当于在原来的基础上，通过⽤⼾对于文章的兴趣 偏好，对embedding的各个维度进⾏加权，提升不同维度的贡献程度。相当于只提取了更加重要的⼀ 些维度信息。 既节省了计算量，⼜避免维度冗余。

所以我上面那个设计图里面就引入了这个操作。 事先指定好了lhuc_feature，比如用户id和item id的拼接，然后是原始的特征向量拼接，过DNN的时候，采用了lhuc_net的设计对每层输出加权。 另外，还有个尝试就是对于类别型的特征向量拼接起来，过了一个双线性交互层(FibiNet的那个)， 其实本来想手动实现FFM的，因为我见到过手动指定交互有意义的特征，比如[user_id, (doc_id, doc_字数, doc_类别)]，相当于用户与后面这三个交互，那么用户这里就会有三个域向量分别与后面的哈达玛积，然后求和这样，就实现了手动FFM，但是具体代码实现的时候，发现这个域向量不知道从embedding层怎么拿到了，毕竟这里用户id对应了三个不同embedding。卡了会发现这次重点不在这里，于是就用双线性交互代替了。 双线性交互的输出依然是过lhuc_net。 然后把这个输出与刚才原始特征过lhuc_net的输出拼接起来，再过一个全连接层sharedlast，得到的输出分别过两个任务task_tower。

所以这里就有了shared bottom结构，并且这里也知道共享层的最后一层参数就是sharedlast这个全连接的参数(图里面的底部最后的共享层)。 模型代码如下：

def SharedBottom(dnn_feature_columns, lhuc_feature_columns, bottom_dnn_hidden_units=(256, 128), tower_dnn_hidden_units=(64, ), 
                l2_reg_embedding=0.00001, l2_reg_dnn=0, seed=2021, dnn_dropout=0, dnn_activation='relu',
                dnn_use_bn=False, task_types=('binary', 'binary'), task_names=('ctr', 'ctcvr'), bilinear_type='interaction'):
    
    num_tasks = len(task_names)
    
    # 异常判断
    for task_type in task_types:
        if task_type not in ['binary', 'regression']:
            raise ValueError("task must be binary or regression, {} is illegal".format(task_type))
    
    # 构建Input层并将Input层转成列表作为模型的输入
    input_layer_dict = build_input_layers(dnn_feature_columns)
    input_layers = list(input_layer_dict.values())
    
    # 筛选出特征中的sparse和Dense特征， 后面要单独处理
    sparse_feature_columns = list(filter(lambda x: isinstance(x, SparseFeat), dnn_feature_columns))
    dense_feature_columns = list(filter(lambda x: isinstance(x, DenseFeat), dnn_feature_columns))
    
    # 获取Dense Input
    dnn_dense_input = []
    for fc in dense_feature_columns:
        dnn_dense_input.append(input_layer_dict[fc.name])
    
    # 构建embedding字典
    embedding_layer_dict = build_embedding_layers(dnn_feature_columns)
    # 离散的这些特特征embedding之后，然后拼接，然后直接作为全连接层Dense的输入，所以需要进行Flatten
    dnn_sparse_embed_input = concat_embedding_list(sparse_feature_columns, input_layer_dict, embedding_layer_dict, flatten=False)
    
    # 把连续特征和离散特征合并起来
    bias_input = combined_dnn_input(dnn_sparse_embed_input, dnn_dense_input)
    
    # 下面dnn_sparse_embed_input进行双线性交互
    bilinear_out = BilinearInteraction(bilinear_type=bilinear_type)(Concatenate(axis=1)(dnn_sparse_embed_input))
    
    # lhuc_features_columns
    lhuc_input = concat_embedding_list(lhuc_feature_columns, input_layer_dict, embedding_layer_dict, flatten=True)
    lhuc_input = concat_func(lhuc_input)
    
    # bilinear_out与lhuc_input过lhuc_net
    bilinear_out_flatt = Flatten()(bilinear_out)
    bilinear_lhuc_out = lhuc_net("bilinear_lhuc", bilinear_out_flatt, lhuc_input)
    
    # bias_input与lhuc_input过lhuc_net
    bias_lhuc_out = lhuc_net("bias_lhuc", bias_input, lhuc_input)
    
    # 两个输出拼接就是双线性net的最终输出结果，汇总了原始信息和交叉信息， 且通过lhuc_net对维度加权，在DNN每一层做一个维度筛选
    sb_out = Concatenate(axis=-1)([bilinear_lhuc_out, bias_lhuc_out])

    sb_out = DNN((64, ), dnn_activation, l2_reg_dnn, dnn_dropout, dnn_use_bn, seed=2022, name='sharedlast')(sb_out)
    
    # 每个任务独立的tower
    task_outputs = []
    for task_type, task_name in zip(task_types, task_names):
        # 建立tower
        tower_output = DNN(tower_dnn_hidden_units, dnn_activation, l2_reg_dnn, dnn_dropout, dnn_use_bn, seed=2022, name='tower_'+task_name)(sb_out)
        logit = Dense(1, use_bias=False, activation=None)(tower_output)
        output = PredictionLayer(task_type, name=task_name)(logit)
        task_outputs.append(output)
    
    model = Model(inputs=input_layers, outputs=task_outputs)
    return model

到这里模型这块算是探索完毕，具体详细代码可以参考后面的GitHub链接。这里之所以先用篇幅说这个，是因为这里是为后面相关loss权重自适应实验铺好了基础。接下来的几篇paper都是如何自适应调整loss权重的， 我打算统一都基于这个雏形复现它们，然后简单的跑跑。 虽然效果可能无法对比，但有代码，能跑，心里就特别踏实哈哈。

4. Gradnorm(梯度标准化的方式自适应平衡多个任务之间的loss)

这是2018年发表在ICML上的一篇paper， 全称是《Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks》， 这篇paper里面提出了一个非常厉害的观点：任务不平衡会阻碍模型的训练，而这种阻碍其实体现在了反向传播时参数的梯度不平衡。所以作者就考虑，能不能通过动态调整每个任务的loss权重，来让参数的梯度保持平衡呢？ 这类似于一种逆向思维的方式，答案当然是能。 作者提出的Grannorm方法非常的巧妙且实用，所以下面详细剖析下这种方法是啥，以及怎么自适应平衡多任务loss的？

4.1 Introduction

作者在引言部分就提到了多任务学习的关键思想：

然而目前大多数多任务学习的研究，都是把重点放到了网络结构的优化或者是数据优化方面，但他们忽略了一个关键的问题：

比如， 一个任务在训练的过程中占据主导， 必然会体现在对网络参数更新的时候， 该任务能传回大幅度的梯度回来，以此表达它的主导地位，使得网络参数更新几乎是基于了这个任务传来的梯度。

所以，作者说：

那么如何动态的调整$w_i$让每个任务得到平衡呢？ 这里提出的方法，就是希望每个任务loss的量级或者说对参数的梯度量级要尽量接近， 希望不同的任务以相似的速度学习。 即想在模型训练过程中，如果发现当前某个任务的loss量级很大(梯度量级大)或者是某个任务训练过快，此时都应该适当减小这种任务对应的$w_i$，这样就能让那些loss量级小或者训练慢的任务对当前网络更新有更多的影响， 这样就能得到平衡啦。所以，就会发现这种方式是基于网络的训练情况动态把$w_i$学习出来。

那么，具体是怎么做呢？ 这里就直接上方法。

4.2 GradNorm Algoritm原理

这里还是先上多任务的损失函数：
$$L=\sum _i{w}_i(t)\ast L_i$$
这个$t$可以认为是训练到了第$t$次， 作者说，学习$w_i(t)$要基于两个出发点：

1. 将不同任务对参数产生的梯度与一个统一的尺度比较，这样就能推断出它们的相对大小
2. 这个统一的尺度规范要能动态的调整，使得不同的任务以相似的速度训练

当然这么说，可能太抽象， 其实用人话讲，就是我们既然是要在训练过程中根据各个任务的梯度量级和各个任务训练的速度去动态调整每个任务的权重嘛， 就得需要对比出每个任务的参数梯度到底是大还是小？ 每个任务目前训练的是快还是慢？

所以，下面首先要定义一些变量来衡量任务的loss量级或者梯度量级，以及任务训练的快慢等。 这些都是Gradient Normalization算法的核心变量， 要好好理解。

• $W$: 这个不用多说，就是网络的参数嘛， 不过这里一般选shared layer的最后一层参数，能节省计算量， 所以算是网络所有参数的一个子集$W\subset \mathcal{W}$
• $G_W^{(i)}(t)={\Vert {\nabla }_W{w}_i(t)L_i(t)\Vert }_2$：这个是每个单任务$w_i(t)L_i(t)$对于参数$W$的梯度的二范数，表示的是当前第$t$次训练里面，每个任务对于$W$传回的梯度大小。 这个梯度越大，说明了任务主导性就越强，应该也很好理解。 而主导性越强，说明目前的loss量级越大，应该减小$w_i$。
• ${\bar{G}}_W(t)=E_{\text{task }}\left[G_W^{(i)}(t)\right]$： 第$t$次训练里面，各个任务传回的参数梯度范数的平均值(上面那个求了个平均)， 有了这哥们之后，我们就能看出每个任务对参数梯度的相对大小来了。这个就是上面所说的统一的尺度关于梯度量级的那部分衡量。

上面这三个变量，主要是看各个任务对参数梯度量级的， 下面介绍两个衡量当前任务训练快慢的：

• ${\tilde{L}}_i(t)=L_i(t)/L_i(0)$： $t$次迭代的loss值与迭代之前的loss比值， 这个东西一定程度上衡量了$i$任务的反向训练速度。
• $r_i(t)={\tilde{L}}_i(t)/E_{\text{task }}\left[{\tilde{L}}_i(t)\right]$： 这个就是归一化的上面那东西，叫做相对反向训练速度，即各个任务之间的训练速度有了可比性，即$r_i(t)$越大，说明${\tilde{L}}_i(t)$越大，说明$L_i(t)$越大， 而这个越大，说明loss下降的幅度小，这个任务训练的慢

这样，衡量不同任务loss的量级以及不同任务训练速度的指标就定义出来了，有了这俩东西之后，上面我们说，不同任务之所以有的占主导，就是因为在训练过程中，有的loss量级或者是反向传播传回的梯度量级各个任务参差不齐，差距悬殊。 那么，如果我们能通过调整每个任务的$w_i$，使得每个任务在$t$次迭代时，梯度都能尽可能满足下面这个式子：
$$G_W^{(i)}(t)\mapsto {\bar{G}}_W(t)\times {\left[r_i(t)\right]}^{\alpha }$$
就能使得每个任务传回的梯度相差不大，就都能对网络的参数更新产生贡献差不多啦。也就是达到了一个所谓的“平衡”。

这个表示的其实就是在每一次迭代的时候， 动态调整$w_i$，尽量让每个任务传回的梯度尽量往${\bar{G}}_W(t)\times {\left[r_i(t)\right]}^{\alpha }$靠近，为啥是这么个东西呢？ 我们知道前者是每个任务传回梯度的一个平均值，能够衡量各个任务参数梯度或者loss的量级大小，而后者衡量的是各个任务训练的速度快慢，靠近这俩的乘积，就能既考虑各个任务的梯度量级，也能考虑各个任务的训练速度，相当于从两方面进行了权衡。

再说这里的$\alpha$，这个东西是一个超参数，需要事先设置。 起的依然是一个放大器的作用。如果某个任务$r_i(t)$本身很大，再有这个$a$buff加成，可能就会让这个任务的训练速度更大。

• 如果多个任务相差很大，导致学习速度有显著的不同时，可以适当增大$alpha$，强迫把他们的训练速度拉到一个平衡
• 如果相差不大，考虑更小的$alpha$
• 如果$alpha=0$， 那就相当于不考虑训练速度，只考虑梯度的量级了

上面只是直观的描述哇， 因为上面只是说动态的调整$w_i$，让各个任务传回的梯度更接近右边那个值。 那究竟咋动态的调整呢？ 这里作者的思路是把$w_i$也看成参数，然后根据上面这个，定义了一个损失函数，用来衡量每个任务的loss权重$w_i(t)$的好坏， 这个叫做gradient loss：
$$L_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}}\left(t;w_i(t)\right)=\sum _i{\left|G_W^{(i)}(t)-{\bar{G}}_W(t)\times {\left[r_i(t)\right]}^{\alpha }\right|}_1$$
这个其实和我们训练神经网络的参数一个道理，训练神经网络参数也是通过调整权重让其有一个合理的输出，直观来看：

• $G_W^{(i)}(t)$与${\bar{G}}_W(t)$平衡不同任务loss的量级，当某个任务loss过大或者过小，$G_W^{(i)}(t)$与${\bar{G}}_W(t)$的距离就会变大， loss增加，从而下一步更新$w_i$使得loss量级接近
• $r_i(t)$衡量不同任务训练速度，当任务训练速度过快，$r_i(t)$减小，loss增加
• 还要注意一点，就是损失对$w_i$求导的时候， ${\bar{G}}_W(t)\times {\left[r_i(t)\right]}^{\alpha }$是个常数， 因为能根据各个loss传回的梯度以及$r_i(t)$计算出来，这样求导其实只有前面的$G_W^{(i)}$

每一次训练，通过损失函数，依然是梯度下降的方式动态更新$w_i$。

$$w_i(t+1)=w_i(t)+\lambda \ast \mathrm{Gradient}\left(GL,w_i(t)\right)$$
综上， 就能得到GradNorm的训练流程了：

翻译过来就是：

1. 初始化各个loss的权重为1，初始化网络参数，配置$\alpha$的值，初始化参数$W$
2. 通过加权求和的方式计算网络的loss
3. 计算每个任务的梯度标准化的值$G_W^{(i)}(t)$，相对反向训练速度 $r_i(t)$
4. 计算全局梯度标准化的值${\bar{G}}_W(t)$
5. 计算Gradient Loss
6. 计算Gradient Loss对$w_i(t)$的导数
7. 更新$w_i(t)$
8. 更新整个网络参数
9. 第7步的结果renormalize一下，使得$w_i(t)$的和等于任务数量

这里主要是说下最后一步我的理解，这里需要把所有任务的权重重新归一化一下。

因为如果这个$w_i$之和不加限制， 整体和变小的话，最后就导致网络训练不动了， 并且这样玩的话损失降低就有可能是由于$w_i$变小的原因，而不是每个任务的损失在变小，所以必须控制住多个任务的$w_i$和是具体范围。

下面是作者给出的答案：

4.3 代码实现

接下来， 从代码的层面看这个算法的细节。 第二节已经搭建好了SharedBottom模型，

model = SharedBottom(dnn_features_columns, lhuc_feature_columns, tower_dnn_hidden_units=[], task_types=['regression', 'binary'], 
             task_names=['duration', 'click'])

接下来就是看看如何实现gradnorm算法， 来指导SharedBottom模型进行训练。这里也是踩了很多坑，卡了很久的。 但有了这个开始，相信后面的paper思路就容易了。这里说下两个重点：

1. 这里模型训练，不能采用tf的高级API，也就是model.fit()这种形式，因为gradnorm这里需要每个task求到loss之后，要用这个loss对shared bottom最后一层W参数求梯度的，然后是定义梯度损失，更新loss的权重$w$， 这个过程如果model.fit是无法人为控制的。这也是高级API存在的问题，虽然简单易用，但灵活性不够。 所以这里我采用了tf的中级训练API，也就是自己写train_step，手动写前向传播，计算损失，反向传播与参数更新过程。和pytorch类似。代码如下：

   # 模型训练这里，需要用到底层的训练脚本，这里不能用高层keras的API
   optimizer = tf.keras.optimizers.Adam(learning_rate=0.005)
   
   train_loss = tf.keras.metrics.Mean(name='train_loss')
   train_reg_loss = tf.keras.metrics.Mean(name='train_reg_loss')
   train_bin_loss = tf.keras.metrics.Mean(name='train_bin_loss')
   loss_func = {"binary": tf.keras.losses.binary_crossentropy, "regression": tf.keras.losses.mean_squared_error}
   
   @tf.function
   def train_step(features, labels, task_types, weight):
       losses = []
       gnorms = []
      
       with tf.GradientTape() as tape:
           # 遍历每个任务
           for i, task_type in enumerate(task_types):
               out = model(features, training=True)
               task_loss = loss_func[task_types[i]](out[i], labels[i])
               # print("task_loss", task_loss)
               losses.append(weight[i] * task_loss)
                   
           # 这里更新
           loss = tf.add_n(losses)
           gradients = tape.gradient(loss, model.trainable_variables)
           
       # 更新所有W参数
       optimizer.apply_gradients(zip(gradients, model.trainable_variables))
       
       train_loss(loss)
       train_reg_loss(losses[0])
       train_bin_loss(losses[1])
       
       return loss, losses[0], losses[1]
   

   这样遍历epoch的时候，拿到当前批次的样本，然后过上面的这个函数即可训练模型。

2. 既然这里使用中级API，数据方面需要在原来的基础上，自己构建数据管道， 这里推荐看一个教程叫做20天吃掉TensorFlow， 我是在那里面找的构建数据管道方法：

   # 构建数据管道
   train_ds = tf.data.Dataset.from_tensor_slices((train_model_input, (label_duration, label_click))).shuffle(buffer_size=100).batch(128).prefetch(tf.data.experimental.AUTOTUNE)
   

有了数据，有了训练步骤，那么就可以写模型训练函数了。

epochs = 10
best_test_loss = float('inf')
task_types = ["regression", "binary"]

task_weight = [tf.Variable(1.0, trainable=True), tf.Variable(1.0, trainable=True)]

grad_norm = True

for epoch in tqdm(range(1, epochs+1)):
    
    print(task_weight)
    train_loss.reset_states()
    train_reg_loss.reset_states()
    train_bin_loss.reset_states()

    for feature, labels in train_ds:
        if grad_norm:
            loss, loss_reg, loss_bin, task_weight_grads = train_step_gradnorm(feature, labels, task_types, task_weight)
        else:
            loss, loss_reg, loss_bin = train_step(feature, labels, task_types, task_weight)
    
    if grad_norm: 
        # 更新权重参数  
        # 这里的一个坑： 这个一定要放到epoch下更新w，不能放到train_step里面，放到里面，相当于每个batch级更新
        # 而每个batch差别很大，经过几个batch级别的迭代，这里的loss就会变成nan， 一定要放到外面
        optimizer.apply_gradients(zip(task_weight_grads, task_weight))
        
        # 如果两者某一个出现了nan
        if tf.compat.v1.is_nan(task_weight[0]) or tf.compat.v1.is_nan(task_weight[1]):
            task_weight = [tf.Variable(1.0, trainable=True), tf.Variable(1.0, trainable=True)]
            
        else:
            #weight参数需要renormalize下   这里如果不renormalize， 更新完的梯度会有nan值，此时会造成loss直接变成nan
            coef = tf.math.divide(2.0, tf.add(task_weight[0], task_weight[1]))
            
            task_weight = [tf.Variable(tf.multiply(task_weight[0], coef), trainable=True), 
                           tf.Variable(tf.multiply(task_weight[1], coef), trainable=True)]
            
        
    template = 'Epoch {}, Loss: {} - regression_loss: {} - binary_loss: {}'
    print(template.format(epoch, train_loss.result(), 
                          np.mean(loss_reg), 
                         np.mean(loss_bin)))

当然，这个是加入了grad_norm算法。如果不使用grad_norm，那么代码非常简单，直接遍历epoch，然后训练每个batch，输出损失即可。 并且这里还能手动指定每个loss的权重task_weight， 按照gradnorm初始化的定义，两个任务权重相等，设置成1。

接下来， 说说gradnorm算法加入的逻辑，首先，指定的task_weight， 要声明成Variable的格式，且能被训练(这个变量在修改上也是踩了很多坑，tf.1构建静态图的时候定义变量用的，修改的时候要用.assign函数才能改值。但tf1构建好静态图之后，开启会话统一执行，sess.run(w.assign(1.0))的时候才真正改到Variable变量w的值。 而tf2成了动态图，没有了会话一说，虽然可以直接通过w=w.assign(1.0)修改w的值，但是这个值会变成Unreadable Variables， 这时候对loss加权使用就变成NoneType，贼坑，卡了我好久，但不知道tf2有没有直接定义可训练参数的简单操作)。

声明完了权重之后，然后把grad_norm设置为True， 在每次batch迭代的时候，就走下面的train_step_gradnorm脚本，我把gradnorm算法的实现放到了这个里面。具体如下：

#@tf.function
def train_step_gradnorm(features, labels, task_types, weight):
    losses = []
    gnorms = []
    
    # RuntimeError: GradientTape.gradient can only be called once on non-persistent tapes
    # 这是因为GradientTape 占用的资源默认情况下dw = t.gradient(loss, w)计算完毕就会立即释放
    # 如果连续计算微分， 指定persistent=True
    with tf.GradientTape(persistent=True) as tape:
        # 遍历每个任务
        for i, task_type in enumerate(task_types):
            out = model(features, training=True)
            task_loss = loss_func[task_types[i]](out[i], labels[i])
            losses.append(weight[i] * task_loss)
                
        # 这里更新
        loss = tf.add_n(losses)
        gradients = tape.gradient(loss, model.trainable_variables)
        
        # 使用grad_norm
        
        # 第一步： 拿到每个任务对于最后一个共享层的梯度
        # # 获取到loss对最后一层共享层的梯度  这里需要对最后一个共享层参数计算一遍微分
        G1R = tape.gradient(losses[0], model.get_layer('sharedlast').trainable_variables)[0]  # 这里只用w， 不用b
        G1 = tf.norm(G1R, ord=2)   # 求二范数
        G2R = tape.gradient(losses[1], model.get_layer('sharedlast').trainable_variables)[0]
        G2 = tf.norm(G2R, ord=2)  
        
        # 第二步： 计算平均梯度
        G_avg = tf.math.divide(tf.add(G1, G2), 2)

        # 第三步： L_hat_i 表示当前任务训练程度
        l_hat_1 = tf.math.divide(tf.keras.backend.mean(losses[0]), tf.math.log(2.))
        l_hat_2 = tf.math.divide(tf.keras.backend.mean(losses[1]), tf.math.log(2.))
        l_hat_avg = tf.math.divide(tf.math.add(l_hat_1, l_hat_2), 2)

        # Inverse training rates r_i(t)   tf2.x 不能tf.div， 移除了这个函数
        inv_rate_1, inv_rate_2 = tf.math.divide(l_hat_1, l_hat_avg), tf.math.divide(l_hat_2, l_hat_avg)

        # 放大系数alpha
        a = tf.constant(0.5)
        C1 = tf.multiply(G_avg, tf.pow(inv_rate_1, a))
        C2 = tf.multiply(G_avg, tf.pow(inv_rate_2, a))
        # 看成常数， 不计算梯度
        C1 = tf.stop_gradient(tf.identity(C1))
        C2 = tf.stop_gradient(tf.identity(C2))

        # 第五步： 定义grad_loss
        loss_gradnorm = tf.math.add(
            tf.reduce_sum(tf.abs(tf.subtract(G1, C1))),
            tf.reduce_sum(tf.abs(tf.subtract(G2, C2))))
        

        # 第六步： 求权重的梯度
        weight1_grad = tape.gradient(loss_gradnorm, weight[0])
        weight2_grad = tape.gradient(loss_gradnorm, weight[1])
        weight_grads = [weight1_grad, weight2_grad]
            
    
    # 更新所有W参数
    optimizer.apply_gradients(zip(gradients, model.trainable_variables))
    
    
    train_loss(loss)
    train_reg_loss(losses[0])
    train_bin_loss(losses[1])
    
    return loss, losses[0], losses[1], weight_grads

大体逻辑的话，首先是前向传播求梯度这块，需要在GradientTape里面指定persistent=True参数，否则默认是只能求一次梯度的，而这里我们显然需要进行好几次微分操作。遍历每个task，前向传播得到损失。然后加权求和得到最终的loss值。

有了loss，用tape.gradient函数获得模型所有参数的梯度。 这个是用来更新模型参数的

接下来，进入grad_norm算法环节:

1. 拿到每个任务的loss，分别对最后一个共享层参数求导，拿到梯度，然后求二范数得到$G_w^i(t)$，然后二范数平均，得到$\overline{G_w}(t)$

   # 第一步： 拿到每个任务对于最后一个共享层的梯度
   # # 获取到loss对最后一层共享层的梯度  这里需要对最后一个共享层参数计算一遍微分
   G1R = tape.gradient(losses[0], model.get_layer('sharedlast').trainable_variables)[0]  # 这里只用w， 不用b
   G1 = tf.norm(G1R, ord=2)   # 求二范数
   G2R = tape.gradient(losses[1], model.get_layer('sharedlast').trainable_variables)[0]
   G2 = tf.norm(G2R, ord=2)  
   #计算平均梯度
   G_avg = tf.math.divide(tf.add(G1, G2), 2)
   

2. 计算$L_i(t)$以及$r_i(t)$

   # L_hat_i 表示当前任务训练程度
   l_hat_1 = tf.math.divide(tf.keras.backend.mean(losses[0]), tf.math.log(2.))
   l_hat_2 = tf.math.divide(tf.keras.backend.mean(losses[1]), tf.math.log(2.))
   l_hat_avg = tf.math.divide(tf.math.add(l_hat_1, l_hat_2), 2)
   
   # Inverse training rates r_i(t)   tf2.x 不能tf.div， 移除了这个函数
   inv_rate_1, inv_rate_2 = tf.math.divide(l_hat_1, l_hat_avg), tf.math.divide(l_hat_2, l_hat_avg)
   

3. 引入放大系数$\alpha$， 然后得到每个梯度要趋近的目标尺度值

   # 放大系数alpha
   a = tf.constant(0.5)
   C1 = tf.multiply(G_avg, tf.pow(inv_rate_1, a))
   C2 = tf.multiply(G_avg, tf.pow(inv_rate_2, a))
   # 看成常数， 不计算梯度
   C1 = tf.stop_gradient(tf.identity(C1))
   C2 = tf.stop_gradient(tf.identity(C2))
   

4. 定义grad_loss

   # 第五步： 定义grad_loss
   loss_gradnorm = tf.math.add(
        tf.reduce_sum(tf.abs(tf.subtract(G1, C1))),
        tf.reduce_sum(tf.abs(tf.subtract(G2, C2))))
   

5. 求权重的梯度

   # 求权重的梯度
   weight1_grad = tape.gradient(loss_gradnorm, weight[0])
   weight2_grad = tape.gradient(loss_gradnorm, weight[1])
   weight_grads = [weight1_grad, weight2_grad]
   

   这样，求完了之后，要把这个梯度返回回来，因为这算是每个batch里面得到的梯度了。

   if grad_norm:
       loss, loss_reg, loss_bin, task_weight_grads = train_step_gradnorm(feature, labels, task_types, task_weight)
   

6. 更新权重，并进行重新归一化

   if grad_norm: 
       # 更新权重参数  
       # 这里的一个坑： 这个一定要放到epoch下更新w，不能放到train_step里面，放到里面，相当于每个batch级更新
       # 而每个batch差别很大，经过几个batch级别的迭代，这里的loss就会变成nan， 一定要放到外面
       optimizer.apply_gradients(zip(task_weight_grads, task_weight))
           
       # 如果两者某一个出现了nan
       if tf.compat.v1.is_nan(task_weight[0]) or tf.compat.v1.is_nan(task_weight[1]):
           task_weight = [tf.Variable(1.0, trainable=True), tf.Variable(1.0, trainable=True)]
               
       else:
           #weight参数需要renormalize下   这里如果不renormalize， 更新完的梯度会有nan值，此时会造成loss直接变成nan
           coef = tf.math.divide(2.0, tf.add(task_weight[0], task_weight[1]))
               
           task_weight = [tf.Variable(tf.multiply(task_weight[0], coef), trainable=True), 
                          tf.Variable(tf.multiply(task_weight[1], coef), trainable=True)]
   

   这块其实遇到了几个神级之坑， 第一个就是更新权重的这个操作，别放到每个batch里面，因为每个batch差别很大，如果放到里面的话，一个epoch之后，损失就变成nan了，因为回归和分类loss幅度相差的太大了，如果放到batch里面更新，分类的loss权重很快就变成nan。 当然我突然发现我这里也有一个代码bug， 就是这里采用的task_weight_grads其实是最后一个batch的，这地方正确的写法应该是每个epoch开始弄一个累加器，求每个batch的梯度和，然后用平均值来更新。 另外，就是即使放到epoch外更新，也有可能两三个epoch就把权重更新成nan，这时候要注意判断，如果出现nan了，重新指定权重。 但这地方注意是重新定义Variables对象了，这时候一定要注意train_step_gradnorm上面的@tf.function注释掉，否则这里报# TypeError: weak object has gone away， NoneType object has no attribute 'shape' 。 这是因为@tf.function 不回溯静态图，此时不能重新定义一个对象。如果您希望不同的对象具有不同的跟踪，即不共享跟踪，您可以使用不同的 @tf.function 对象。 这个意思就是说，如果一个函数上面用了@tf.function修饰了，那么就和唯一的Variable对象绑定了，如果此时试图重新建Variable，然后调用这个函数，此时就会报上面这个错误，需要重新定义一个函数才行。 这个是很坑， 我在这里尝试了各种操作，最后竟然去掉修饰才有最优解。 最后面的就是权重重新归一化的代码了。

这样完事之后，至少能跑起来了：

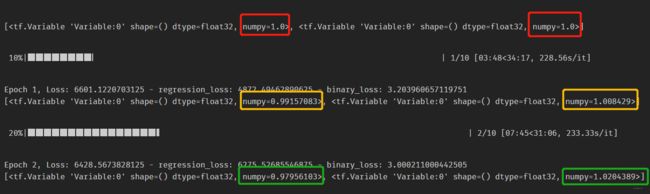
也会发现，每迭代一次权重就会进行更新，由于回归loss和分类loss相差的太大了，基本上回归loss占主导，于是乎，算法试图慢慢的把分类loss的权重调大， 回归loss的权重减小。 但这个训练过程实在是太慢了。 我不知道是幅度差的太大，还是学习率，$\alpha$参数设置的问题，还是硬件限制，总之在我小本子跑，采样了好几次，这才刚刚跑起来。 也有可能是把persistent=True之后，特别耗显存。 不过，看到它跑起来，然后还在work，心里确实会踏实很多。

这样也就更能理解GradNorm算法了。 训练了10个epoch的效果：

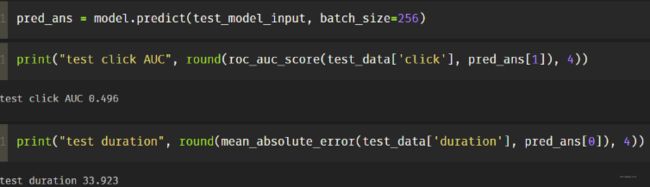
回归这个依然是占主导，这个训练的还可以， 但是分类那个不行。 下面这个是我手动指定两个loss的权重，回归权重0.02， 分类权重0.98的结果：

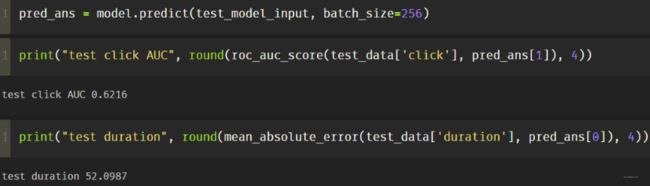
这个的话，分类和回归效果就相对好一些， 通过gradnorm调权重，虽然回归的在降， 分类的在升，但是太慢了。

GradNorm的探索就到这里了，详细的实验及代码，见我后面的GitHub链接吧。

关于GradNorm简单总结：

• 优点: Gradient Normalization既考虑loss的量级，又考虑不同任务训练速度
• 缺点：
  • 每一步迭代都需要额外计算梯度， $W$参数多的时候，会影响训练速度，要保留计算图，实在是太耗显存了。
  • 此外，$L_i(0)$过于依赖于参数初始值， 如果初始值很大，paper建议用其他值代替，比如分类任务，可以用$log(c)$代替，$c$是分类数量。 但我上面实验中，回归任务初始值也用了这个数，我感觉最终结果差也与这个有关。
• 另外还有一点，就是我看到有实现这个算法的时候， 会把Label loss和gradient loss相加得到总的loss， 然后统一优化参数。 但是这个操作我不知道是怎么优化权重参数的，代码怎么写。反正我是觉得这两种loss应该独立优化，不能相加，paper里面的意思应该也是这样。

5. Dynamic Weight Averaging(动态加权平均)

这是2019年CVPR上的一篇paper《End-to-End Multi-Task Learning with Attention》，这里面提出了一个动态加权平均的策略来确定各个任务loss权重，DWA的核心是希望各个任务以相近的速度来进行学习。

但是看完paper之后，才发现这篇文章的核心并不是讲动态加权平均，看论文名字也知道，其实它的核心是提出了一个带有注意力机制的多任务学习模型框架，给我的感觉就是在原来的shared bottom的基础上， 在每个任务tower里面加入注意力层来对shared bottom的共性特征进行一波筛选，选出对自己任务有用的特征，然后走task_tower。这样就能更好的学习task-specific特征了。下面这段就是整篇paper的核心：

这里之所以把这大段话都拿过来，是因为这个句式我觉得也非常漂亮，特别适合写论文介绍自己的工作用。

而通过DWA来确定损失函数的权重，只在后面实验里面提了一下， 所以并不是paper的主流，相比于gradnorm，这个DWA也要简单许多。 所以在介绍DWA之前，还是先介绍下提出的MTAN模型，虽然这个模型无非就是在每个任务之前加注意力，但是这个设计又给了我一点新的启发，然后再看下DWA是怎么玩的。

5.1 Multi-Task Attention Network

作者在引言中也提到了多任务协同有很多好处，不仅有利于模型的高效训练，还能让模型学习多个任务的同时优势互补，来缓解过拟合能力，各个任务之间还能互享底层的共享特征，但作者也意识到，能够让模型较为成功的学习共享表征主要是两个挑战，其实这两个挑战就是目前在多任务学习中研究的两个主要热点：

1. 模型架构方面： 也就是如何设计一个好的模型结构来学习共享特征， 上面整理了hard shared bottom和soft shared bottom， 这种设计的标准必须尽可能学习到广义的特征(可以避免过拟合)，也能学习到每个任务特定的特征表示(可以避免欠拟合)
2. 损失函数优化: 也就是模型训练中如何平衡每个任务， 设计标准是保证所有任务要同等关注，不能让容易学习的任务把节奏带偏。

以往的工作可能仅仅在上面某个挑战上发力， 而这篇paper同时在两个挑战上发力，即提出了一个带有注意力的多任务学习模型，又提出了一种loss动态加权的学习策略， 做到了“鱼和熊掌得兼”。

由于之前有了多任务的模型基础， 这里就直接看MTAN网络：

这篇论文解决的多任务是CV领域的语义分割和深度预测任务。 右图是MTAN的网络结构， 就是我们上面的shared bottom范式， 只不过在task_tower之前，加入了Attention Network， 来对底层的共享特征进行特定任务的选择，可以理解成只要对当前任务有用的那些shared features。

那我们可能想，这不是很简单？ 也不见得有多大创新。

前向传播过程也一目了然，无非就是输入特征，然后过一个类似DNN的这种共享塔，得到共享特征shared features, 然后走两个tower的时候， 先分别过两个Att_net得到权重，然后加权到共享特征上，然后走每个task_tower得到输出。

其实一开始我也是这么考虑的，本质上也差不多是这么个思路， 不过由于作者是在cv上做多任务嘛， 底层共享特征肯定不能只用最后一层的，于是乎它的这个设计，让我在推荐上对目前shared bottom的使用也进行了一点introspection(内省，论文中刚学到的哈哈)

整个网络的工作原理如下， 本来这是一个Encoder-Decoder架构，但这里只画了Encoder部分，另一部分和这个一样，只不过是对称回去。 玩过CV的对这种很熟悉应该，先降维再升维。

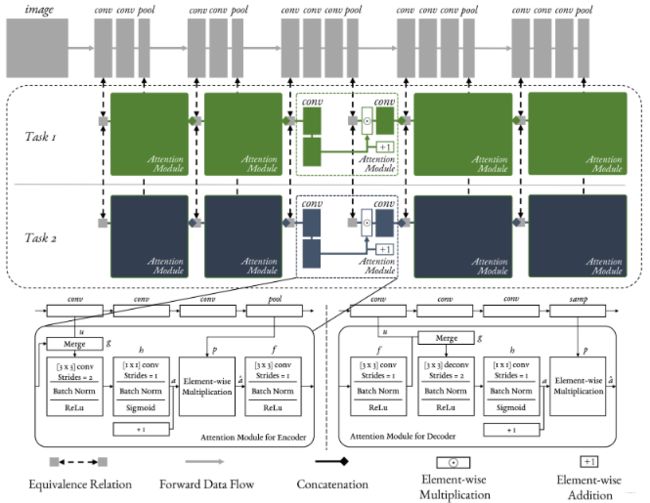
这里主要是弄明白这个网络是怎么走的，MTAN的思路就很清晰了，首先我先解释上面的前向传播过程，然后再类比到推荐中去。

宏观上， 最上面是一个shared bottom， 这里用的是VGG网络用来提取图像的特征，也就是输入是一张图片，然后经过多个【卷积-池化】块去拿到图片的底层特征， 而这些底层特征可以为所有task使用。 因为我们知道图像的特征提取器是从最底层特征，比如纹理，轮廓等，一步步的抽象， 而对于每个图像识别任务，这些底层特征都非常重要。于是乎，每个块的输出特征都能被task使用

这个其实放到推荐上我觉得可能也适用， 而推荐里面无非把卷积-池化换成了DNN，但目前shared bottom貌似是只拿到最后一个层的输出feature，这样会不会也遗漏掉了底层的一些重要信息，也就是特征稍微原始一些的样子，因为DNN层数越多，到了后面越抽象。

所以第一个反思： 推荐里面的shared bottom每一层或者是某些层的DNN输出，是不是也可以类似上面这样利用起来呢？ 这个就类似与W&D架构里面的W侧的那种特征交互，是不是可以为每个task也共享到。 我能想到的两种改进思路：

1. DNN之间加跳远连接，让接近底层的特征有机会也去到共享层，但这样底层特征和高层特征就无脑混合了
2. 像上面这样的设计思路，把某些DNN的重要层的输出直接和最高层输出CONCAT起来，然后过task_tower，也可以把底层特征利用起来。 我觉得这种思路更好，这里不是直接CONCAT起来，而是还加入了Attention进行选择。 （不知道读到这里，有没有联想到上面的什么东西）

这里先开了个脑洞， 下面接着说回上面的结构，shared bottom这块其实很好理解，和我们之前一样，只不过是每一层的特征都有机会为task提供共享特征，这个和我们之前的推荐不同。

这里是两个task， 在task_tower里面加入了Attention Module，对shared bottom每一层的shared features都会有一个特征选择功能。 但猛地一看这个图，可能并没有看懂是啥意思，怎么走的？

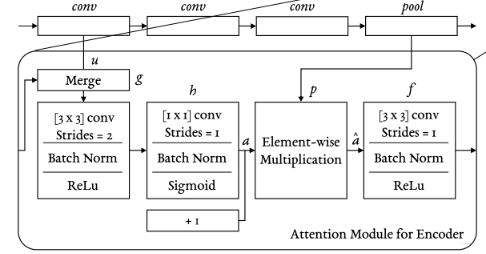
而论文中更是及其简单， 给了这个图，然后给了两个计算公式，就草草了事， 我当时都怀疑，这是顶会paper？ 而这个图经过细品之后，不仅感叹，哇，优美！ 下面是具体的前向传播过程：

输入Img，然后过share-bottom的第一个特征提取块(conv-conv-pool)

1. 过第一个conv之后拿到特征图，会把这个特征图先送到每个task_tower的Attention模块中进行特征筛选。每个Attention模块中的计算过程其实就是下面那个图。我这里单独放一个：
   
   从shared-bottom来的特征图对应图中的$u^1$，这个要先和前面那一层attention module的输出值Concat起来(不过第一层这个除外)。Concat来的特征图，接下来在Attention Module里面过卷积($g$)->卷积($h$)计算出权重$a^1$来(这个就和过两层DNN计算权重一样)。
2. 然后这个权重反乘到了第一个特征提取块的输出特征图上，即这里的$p^1$，这样相当于对第一个特征提取块的输出特征图在channel上进行了特征选择，得到${\hat{a}}^1$， 然后这个东西过卷积层$f$得到了第一个Attention Module的输出$f({\hat{a}}^1)$

这就是每个task对第一个特征提取块提取的共享特征通过Attention Module对共享特征筛选的过程，如果感觉这个过程还是懵， 我再尝试往后面走一个。

share bottom那里走第二个特征提取块(conv-conv-pool)

1. SharedBottom: 接收的第一个shared-bottom的输出特征图$p^1$，然后过第一个conv，拿到特征$u^2$。然后这个特征$u^2$会去每个task_tower。$u^2$在shared bottom中继续往后走，过conv， 过pool得到第二层特征提取器输出$p^2$
2. TaskTower: 对于一个task_tower， 首先这个特征$u^2$会和前面的Attention Module的输出$f({\hat{a}}^1)$做一个Concat， 这个作为第二个Attention Module的输入， 接下来这个Concat的的结果过$g$函数，$h$函数，相当于两层的DNN，得到注意力权重$a^2$。公式如下：$$a_i^{(j)}=h\left(g\left(\left[u^{(j)};f\left({\hat{a}}_i^{(j-1)}\right)\right]\right)\right),j\ge 2$$
   $a^2$对上面第二层特征提取输出$p^2$加权筛选特征，得到${\hat{a}}^2$，公式如下：$${\hat{a}}_i^{(j)}=\left(a_i^{(j)}+1\right)\odot p^{(j)}$$然后这个东西过$f$函数，类似于又非线性一次，得到第二个Attention Module的输出$f({\hat{a}}^2)$

这就是每个task对第二个特征提取块提取的共享特征通过Attention Module对共享特征筛选的过程。而上面接下来会是shared bottom的第三个提取块， 第四个提取块， 第五个提取块。 每个提取块都会经历上面的这个过程。两步：

1. shared bottom对于前面过来的特征图，先经过一个conv提取一波特征，然后这个特征图会去到每个task_tower的Attention Module里面，然后这个特征图也会继续往后走conv-pool得到当前特征提取块的输出。
2. 上面的特征图在每个task_tower塔里面，首先会和前面Attention Module的输出值合并，然后过两层的conv操作得到权重，上面的"+1"是跳远连接的功效，分配率拆开就看出来了。 然后把这个权重反乘到当前特征提取块的输出上，特征筛选完，然全连接或者conv非线性得到当前块的输出。

其实感觉还是挺清晰的吧， 下面进行和推荐shared bottom进行一波类别就更清晰了。直接还是拿推荐里面的shared bottom， 首先看看如何改进能达到上面这样的效果，以及这种效果相比之前的有啥好处？ 这里的shared bottom统一是hard的那种方式哈，MMOE这种底层多个全连接的待会再看。

推荐目前的shared bottom， 底层一个多层DNN， 然后每个task_tower。这个过程不用多说

首先， 把底层的多层DNN搭建的时候，分成好几个特征提取块的方式，也就是类似于多个小的DNN块堆叠起来。然后每个特征提取块，比如两到三层的DNN这样子，第一层的DNN的输出，过task_power里面的Attention Module加权选择

1. 具体操作，就是第一层DNN的输出和前面Attention_net的输出(第一层的除外)，过一个Attention_net，得到权重之后， 反乘到特征提取层的输出上进行特征筛选。

每个特征提取块都经过这样的操作，就是上面这种网络设计的应用。

那这种有什么好处呢？ 之前的shared bottom是输入过多层DNN，然后直接给到每个task tower，这个说是能共享底层特征，但我觉得其实共享不是很充分， 这么多个task，仅仅共享了最后一个网络层的输出向量？ 这个向量真能把所有task的共性特征表达出来？ 我表示怀疑。

所以这种操作的好处是能把shared bottom每一层的特征利用起来，且能在每个task中只选择出对自己有用的特征作为task-specific。 这里设计的巧妙之处就是每个task_tower里面加了注意力模块，这样利用每一层共享特征的时候，变得有了选择。而选择权交给网络自己， 最极端的情况，

$${\hat{a}}_i^{(j)}=\left(a_i^{(j)}+1\right)\odot p^{(j)}$$
这里面的权重都是0， 那么相当于当前Attention Module的输出就是$p^j$，这说明此时利用的是底层的共性特征， 而如果不是全0， 说明对底层共性特征做了一波筛选得到task-specific特征。相当于这个设计，像作者说的，

这个加权操作发现很像lhuc_net的思路，无非就是两者用到的场景不一样而已。

所以，通过这次的MTAN网络设计，就能够得到基于hard shared-bottom改进的第二种范式了，即在每个tower里面加入Attention Module，对shared bottom的每个底层特征都进行筛选，把共性和特性特征做到学习上的统一。

这里可以类比下MMOE的soft hard-bottom的思路，那里是底层设置了很多个专家，每个专家学习不同的共性模式，然后对于不同的task，用门控来选择不同的专家组合，即不同的共性特征模式。 而MTAN是底层类似于设置了一个大的专家，把专家的每一层输出当成不同的共性模式， 然后在task_tower里面，设置了注意力网络对共性模式层层过滤和筛选，得到有用的共性和特性信息。

既然说到了模型范式对比了， 这里简单的再普及下腾讯2020年在RecSys上提出的PLE(Progressive Layered Extraction) 模型，这个模型当时提出的动机觉得MMOE虽然底层这里设置了多个专家，但不同的task都共享这同样的专家，这样task相差太大是不是会有参数的干扰，而产生负迁移？，本质上还是觉得task-specific信息被遮蔽掉了。 于是乎， 在MMOE基础上， 把expert分成了共享专家和每个任务单独的专家， 这样既保留了transfer learning(共享专家)能力，有能有效避免有害参数的干扰(避免negative transfer)。

这个结构本质上没有啥大创新，所以就不单独一篇文章总结了，正好借着这里的对比机会把这个模型也介绍了。 另外这个模型并不像MMOE符合“小而美”的设计思路，虽然比MMOE效果好，但这个是两层呀，用参数换效果。 细节如下：

1. 输入，首先会进入三类专家层组提取特征，每一类专家就和MMOE那种一样了，无非是DNN，映射到多个空间里面去
2. 这里会发现第一层专家输出这里又三个门控机制，对应三类专家，作用的话和MMOE是一样的，左边红色的门控机制，负责给Experts shared和experts A里面的专家加权，中间的只给experts shared专家加权，右边的同样负责共性和特性。加权融合得到了第二层专家的输入
3. 第二层专家这里相当于把第一层专家提取的三类特征， 映射到不同子空间，然后通过第二层门控，这里就只针对的task设置的门控了，加权融合，走task_power。

所以细节点：

1. Gate网络的数量取决于task数量，第一层由于多了个shared gate，所以数量等于task数量+1，第二层gate网络数量与task数量相同
2. 相比较MMoE，PLE除了做了一些创新后，网络结构上深度变深了，变成了2层

OK，关于这篇paper的模型部分就普及这么多，选择了一些对我比较有价值的内容出来，关于里面的一些详细细节，比如语义分割和深度预测是干嘛的，损失函数是啥的等等，大家可以去参考原论文，由于这篇文章是多任务loss优化，这些就先不涉及了。 不过这篇paper还是不错的。 接下来回到正题，动态加权平均。

5.2 Dynamic Weight Average(DWA)

这个可能是作者附加的一个idea， 在paper中用了很小的一部分描述。 在训练多任务的时候， 很难对这些任务的训练进行平衡，上面gradnorm结合了每个任务梯度量级以及训练程度来动态调整每个loss的权重， 来让任务达到平衡。 而这里也从GradNorm中得到启发，提出了这个动态加权平均的方式

同样是考虑了每个task的loss改变比率（这个东西能反应学习难易程度），但是GradNrom需要去访问网络的梯度，而DWA只需要每个任务的loss，这样可以节省很大的内存开销(GradNorm的短板)。

定义每个任务$k$的权重${\lambda }_k$， 其更新公式如下：
$${\lambda }_k(t):=\frac{K\exp \left(\frac{w_k(t-1)}{T}\right)}{{\sum }_i\exp \left(\frac{w_k(t-1)}{T}\right)},w_k(t-1)=\frac{{\mathcal{L}}_k(t-1)}{{\mathcal{L}}_k(t-2)}$$
$w_k(\cdot )$表示的loss的相对下降速率，也就是当前的loss与前一次的loss比值，这个比值越大，就说明当前任务的loss下降的慢， 而下降的慢就说明比较难训练， 下一次理应给他赋予更大的权重。 于是乎，根据左边的公式，如果$w_k$越大， 那么${\lambda }_k$就会越大， 而$\exp$在这里依然是类似于放大器的作用，而整个公式类似于softmax的功效，这里的$T$是温度系数，为了调控任务分布， 越大，说明每个任务分布越均匀，怎么理解？ 假设趋于无穷， 那么每个任务的权重值就一致了，即任务重要性等价了。 而这里为了让所有权重在一个范围内活动，加入了$K$， 保证${\sum }_i{\lambda }_i(t)=K$， 选$K$依然是更加灵活。

所以这个原理要比GradNorm简单，实现起来也比较简单， 作者在这里点了两个细节：

1. 动态更新权重，是在epoch的层面，不能在batch的层面， 这里的损失${\mathcal{L}}_k(t)$是所有batch loss的均值。这样做减少了随机梯度下降和随机训练数据选择的不确定性。 GradNorm的时候走过这个坑
2. 初始化的时候， $t=1,2，w_k(t)=1$，也就是所有task平等看待，当然也可以根据自己的场景情况引入先验的非平衡初始化。

下面简单实现下。

5.3 代码实现

这个代码实现上要比GradNorm可简单太多了， 依然是tf中级API，train_step使用原先简单版本(当然也可以用train_step_gradnorm)，只需要在训练的时候，根据每个任务的训练损失比动态调整权重即可。 唯一需要注意的是动态调整权重所处的位置，是epoch层面。 代码如下：

epochs = 10
K = 2
T = 2
batch_nums = math.ceil(train_data.shape[0] / batch_size)

task_types = ["regression", "binary"]

# 这里的task_weight 就不用tf.Variables了，因为不用梯度更新
task_weight = np.zeros([2, epochs], dtype=np.float32)
avg_cost = np.zeros([epochs, 2], dtype=np.float32)  # reg_loss, bin_loss

dynamic_weight_average = True

for epoch in tqdm(range(epochs)):
    
    # 如果使用动态加权平均，注意依然是epoch层面, 更新权重
    if dynamic_weight_average:
        # 初始化
        if epoch == 0 or epoch == 1:
            w_1 = 1.0
            w_2 = 1.0
            task_weight[0, epoch] = K*np.exp(w_1/T) / (np.exp(w_1/T) + np.exp(w_2/T))
            task_weight[1, epoch] = K*np.exp(w_2/T) / (np.exp(w_1/T) + np.exp(w_2/T))
        else: 
            # 获取每个任务的loss下降比率
            w_1 = avg_cost[epoch-1, 0] / avg_cost[epoch-2, 0]
            w_2 = avg_cost[epoch-1, 1] / avg_cost[epoch-2, 1]
            # 修改权重
            task_weight[0, epoch] = K*np.exp(w_1/T) / (np.exp(w_1/T) + np.exp(w_2/T))
            task_weight[1, epoch] = K*np.exp(w_2/T) / (np.exp(w_1/T) + np.exp(w_2/T))
    else:
        task_weight[0, epoch], task_weight[1, epoch] = 1.0, 1.0
    
    train_loss.reset_states()
    train_reg_loss.reset_states()
    train_bin_loss.reset_states()

    for feature, labels in train_ds:
        loss, loss_reg, loss_bin = train_step(feature, labels, task_types, task_weight[:,  epoch])
        
    # 更新avg_cost train_reg_loss.result算的就是平均损失， 每个batch的平均损失之和/batch_num
    avg_cost[epoch, 0] = train_reg_loss.result()
    avg_cost[epoch, 1] = train_bin_loss.result()
   
    template = 'Epoch {}, Loss: {} - regression_loss: {} - binary_loss:{}, loss_weight: {}-{}'
    print(template.format(epoch, train_loss.result(), 
                          train_reg_loss.result(),
                          train_bin_loss.result(), task_weight[0, epoch], task_weight[1, epoch]))

这个实现起来稍微简单一些，就不用过多解释代码了。 但是通过实验， 发现了几个点：

1. 虽然能在训练过程中动态调整权重，但是这里并不能很好的平衡loss
   
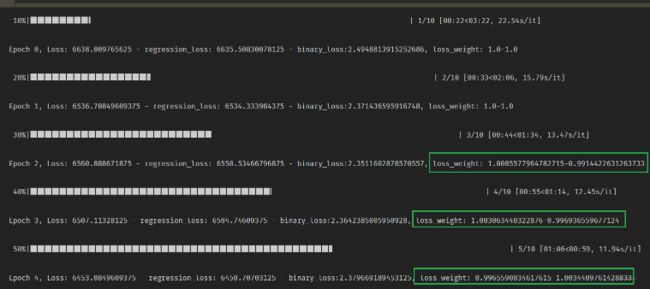
   从这个图里面就能看出来， 显然此时regloss占主导，但迭代的前几次还会增回归损失的权重。后面的几次迭代也会出现这种情况。
2. 用DWA和不用DWA做了一个对比，
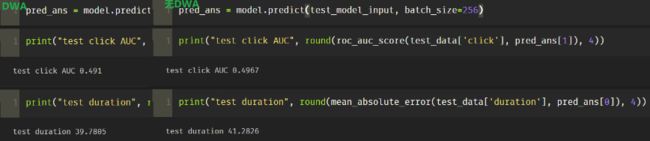
   从对比结果上看，用了DWA之后，反而更偏向于优化主导的任务，也就是回归的任务。使得分类任务效果更加差。

当然我这里的实验并不完备，数量少，模型也不收敛，但通过结果来看，比较直观的结论：对于DWA， 只看loss的下降比率， loss缩小的快的任务， 权重更小，反而会更大，但由于不考虑loss的量级，使得有可能主导任务依然权重很大。 所以本质上感觉并没有平衡多任务的loss。 当然，可能DWA更适用于两个任务很相似的场景， loss量级差不多的情景。

下面对其评价：

• 优点： 只记录不同epoch的loss值，从而避免了为了获取不同任务的梯度， 运算快，节省内存
• 缺点： 没有考虑到不同loss任务量级，需要额外的操作控制各个任务的量级

所以，我感觉不如gradnorm高级，那个东西虽然耗内存，运行慢，但对于task相差很大的loss优化，还真的可以起作用(可以看下上面的实验结果图，gradnorm那里是真的回归损失权重下降，分类任务损失权重上升的)。

6. Dynamic Task Prioritization(动态任务优先级)

这是2018年ECCV上的一篇paper《Dynamic task prioritization for multitask learning》， 这里面的主要思想是希望让更难学的任务具有更高的权重。

所以这篇文章的行文逻辑就比较清晰了，那就是如何定义指标去衡量各个任务之间的难度，以及如何根据这个难度自适应的去调整loss的权重，把较为困难的任务loss更大一些，即花费更大的精力去搞更难的事情才更有效率(idea来自我们的人类哲学哟)。

而衡量任务的难度等级，主要是分析gradient magnitudes, parameter count, update frequencies三个指标来看。 像之前的gradnorm就是既考虑梯度又考虑更新频率，而DWA是只考虑更新频率等。 另外，他们的出发点还不是很一样，这里也正好掰扯下，就当回顾。

• gradnorm: 它是觉得多个任务学习的时候，任务之间如果不平衡了，就会阻碍，所以提出了梯度归一化策略，尽可能的动态调整权重去使得每一次训练之后，各个任务尽量回归平衡， 而平衡主要就是体现在平均梯度以及更新频率方面。所以这个是既平衡loss等级，又平衡学习速度。
• DWA：觉得损失下降快的任务，应该是比较容易学，于是乎，通过调整权重，让学习速度慢的任务具有更高的权重，所以这个只平衡了学习速度。
• UWL:
• DTP: 引入了一个任务优先级的概念，把各个任务根据难度划分，然后自适应调整权重，聚焦于更难的任务上面。每次训练都是让更难的任务有更高权重。

那么DTP究竟是怎么做到的呢？ 由于前面的各种引言铺垫，在前面的几篇论文中都整理过，差不多一样的套路，所以这里我们就直接进入它的方法方面了。

6.1 Priority Base on Difficulty

这一部分就是本文的核心，主要围绕两个问题：

1. 如何定义任务的优先级？
2. 如何在训练过程中动态调整？

在说问题之前，需要进行准备工作，即把我们之前多任务学习问题在这里重新定义一遍。

首先定义一个按照任务难度从大到小排好序的一个多任务集合：$T=\{T_1,T_2,...T_{|T|}\}$，定义任务难度等级$\mathcal{D}\propto {\kappa }^{-1}$,其中$\kappa$是一个评估模型预测能力的指标，比如accuracy。假设$t$表示第$t$个Task， 那么对于$V_t\in |T|$, 有$\mathcal{D}(T_t)\ge D(T_{t+1})$。

假设每个任务的损失用$L_t(\cdot )$，由于并不是所有样本在所有任务上都有对应的Label值(这个要注意下，虽然可能是多任务，但是可能task所在的样本空间不同，这时候用的虽然是全部样本，但是对于某些任务，其实有些样本没有对应的label)，所以，用${\delta }_{t,i}\in \{0,1\}$表示在Task$T_t$上可以获得的真实样本数据$i$，那么对于某个特定的任务， 其损失计算公式如下：
$${\mathcal{L}}_t(\cdot )=\frac{1}{N}\sum _{i=1}^N{\delta }_{t,i}{L}_t\left(p_t^i,y_t^i\right)$$
那么，多个任务的总损失：
$${\mathcal{L}}_{\text{Total }}=\sum _{t=1}^{|T|}{\lambda }_t{\mathcal{L}}_t$$
这里的${\lambda }_t$表示的就是每个任务的loss权重值。

上面只是复习了下多任务训练中损失最后的计算方法。但会发现这里面出现了新的字母$\kappa$，对于每个任务$T_t$， 我们都会选择一个KPI(key performance indicator) ${\kappa }_t\in [0,1]$。这个东西表示的是每个任务的评估指标，比如准确率，平均查准率这种。衡量的是任务难度，一般准确率越高的任务，就比较容易训练。 在训练过程中，这个东西是采用了指数滑动平均的方式计算：

$${\bar{\kappa }}_t^{(\tau )}=\alpha {\kappa }_t^{(\tau )}+(1-\alpha ){\bar{\kappa }}_t^{(\tau -1)}$$
这里的$\tau$表示的迭代次数。其实就是求一个平均值，$\alpha$控制更关注与当前还是之前。

接下来，再讨论一个东西，叫做focusing parameter，用$\gamma \ge 0$来表示，这个东西衡量任务和样本权重下降的一个比例。这啥意思？

之前不是说每个任务会根据学习难易确定优先级嘛， 这里的优先级其实包含两方面，一方面是样本层级的优先级(Example-Level Prioritization)，一方面是任务层级的优先级(Task-Level Prioritization)。

• Example-Level Prioritization – 难训练的样本优先
  其实就是衡量每个样本学习的难易程度，在训练过程中，会根据这个程度去动态调整每个样本的权重。
  
  首先，我们知道对于每个样本，假设是二分类问题的话，其对应的loss计算如下：
  $$\mathrm{C}\mathrm{E}\left(p_c\right)=-\log \left(p_c\right)\text{ where }{p}_c=\{\begin{array}{ll}p,& \text{ if }y=1\\ 1-p,& \text{ otherwise }\end{array}$$
  这就是普通二分类交叉熵计算公式了，在这个损失的基础上，想让模型更聚焦于那些较难训练的样本，减少简单样本的关注，所以就提出了一个"Focal Loss"的定义，其计算如下：
  $$\mathrm{F}\mathrm{L}\left(p_c;{\gamma }_0\right)=-{\left(1-p_c\right)}^{{\gamma }_0}\log \left(p_c\right)$$
  这里的${\gamma }_0$表示example-level的聚焦参数。当然，上面假设的是分类损失，如果是回归损失的话，那么对于样本$i$产生的损失值$e_i$，只要是$e_i\in [0,1]$，同样和上面一样，用$\mathrm{F}\mathrm{L}\left(e_i;{\gamma }_0\right)$，所以需要事先归一化好。

  怎么理解这个所谓的"Focal Loss"呢？
  
  其实仔细观察就会发现，就是在原来损失的基础上，乘上了$(1-p_c{)}^{{\gamma }_0}$，使得模型"更"聚焦某些样本。

  • 假设某个样本$y=1$，模型预测概率值$p$越接近1，说明样本更容易预测，此时$-log(p_c)=-log(p)$本身就较小，$(1-p_c{)}^{{\gamma }_0}$也非常小，相当于在原来损失上又乘上了一个变小的数，double变小，所以这个东西还是起了一个"放大器"作用，拉大贫富差距，具体拉大的幅度通过${\gamma }_0$控制。
  • 假设某个样本$y=0$, 模型预测概率值$p$越接近1，说明样本更难预测，此时$-log(p_c)=-log(1-p)$就很大了，因为对于该样本，模型预测错了，本身损失惩罚， 再加上$(1-p_c{)}^{{\gamma }_0}=(1-(1-p){)}^{{\gamma }_0}$加持，double变大，于是乎，更难训练的样本会带来更大的损失。

  那么，如果在每个任务的损失里面，把原来计算损失的公式改成"Focal Loss"， 即${\mathcal{L}}_t^{\ast }(\cdot )=\mathrm{F}\mathrm{L}\left(p_c;{\gamma }_0\right)$。就能使得模型训练的时候，自动的根据样本训练的难易程度给样本加权，因为越难训练的样本会带来更大的损失，这样反向传播的时候，该样本就会有更大的梯度值更新参数。

  
  符合之前的动机，希望将更多的资源和精力花费在更难的事情上，这里的更难，不仅是更难的任务，还包括更难的样本。

• Task-Level Prioritization - 难训练的任务优先
  对于每个任务的难度程度，我们之前定义了一个${\kappa }_t\in [0,1]$来衡量，如果${\bar{\kappa }}_t\gg 0.5$，就认为$Tas{k}_t$对模型来说，容易训练。此时，就应该把精力花费在更难训练的任务上。为了衡量任务的难易，这里依然可以用"Focal Loss"， 即$$\mathcal{D}\left(T_t\right)=\mathrm{F}\mathrm{L}\left({\bar{\kappa }}_t;{\gamma }_t\right)=-{\left(1-{\bar{\kappa }}_t\right)}^{{\gamma }_t}\log \left({\bar{\kappa }}_t\right)$$
  这个和上面样本的理解起来同理，任务越简单的话，$\mathcal{D}$就会变小。反之，变大。前面那个依然是放大器加持。${\gamma }_t$调节放大程度。那么这个东西既然可以衡量任务的难易程度，而之前的动机是想把资源聚焦到更难的任务上，那么把这玩意当成损失的权重不就完了？ 于是乎，就有了最终的DTP loss：
  
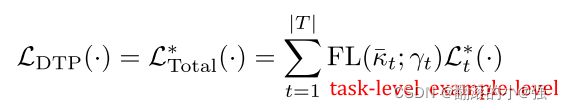
  这个就是加入dynamic task prioritization(DTP)思想之后，最终loss的表现形式。其实就是做了个loss的替换，把之前普通的：
  $${\mathcal{L}}_{\text{Total }}=\sum _{t=1}^{|T|}{\lambda }_t{\mathcal{L}}_t$$
  替换成了：
  $${\mathcal{L}}_{\mathrm{D}\mathrm{T}\mathrm{P}}(\cdot )={\mathcal{L}}_{\text{Total }}^{\ast }(\cdot )=\sum _{t=1}^{|T|}\mathrm{F}\mathrm{L}\left({\bar{\kappa }}_t;{\gamma }_t\right){\mathcal{L}}_t^{\ast }(\cdot )$$
  这样模型在训练的时候，既能考虑每个Task的难易，即$\left({\bar{\kappa }}_t;{\gamma }_t\right)$越大，说明当前任务越难，应该更加聚焦。也能考虑每个样本的训练难易，即${\mathcal{L}}_t^{\ast }(\cdot )=\mathrm{F}\mathrm{L}\left(p_c;{\gamma }_0\right)$，越大，说明样本越难训练，需更加关注。

这就是DTP思想的核心啦。 最后，还给了个对于每个样本求梯度的公式：
$$\frac{\partial }{\partial x}{\mathcal{L}}_{\mathrm{D}\mathrm{T}\mathrm{P}}(\cdot )=\sum _{t=1}^{|T|}\left[\frac{\partial }{\partial x}{\mathcal{L}}_t^{\ast }(\cdot )\right]\mathrm{F}\mathrm{L}\left({\bar{\kappa }}_t;{\gamma }_t\right)+\left[\frac{\partial }{\partial x}\mathrm{F}\mathrm{L}\left({\bar{\kappa }}_t;{\gamma }_t\right)\right]{\mathcal{L}}_t^{\ast }(\cdot )$$
简单看看就好，这东西在代码实现的时候，就不是我们所关心的了。

后面作者也做了一些实验，来验证了这种思想的有效性。

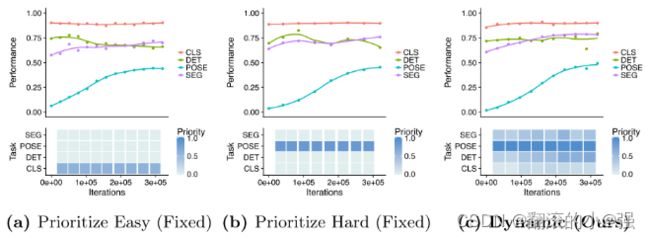
这里的实验是CV里面的四个任务，分类，检测，分割等，前面两个是用的固定权重，区别是一个是最简单的任务给最大权重，一个是最难的任务给最大权重，第三个是动态调整权重，发现第三个里面更难的任务会被训练的更好。 还有详细表格数据对比，这里就不看了，反正好就完事。

6.2 Implicit Priority from the Network Architecture

这个也是论文中感觉有意思的一个点，所以也整理下。

这啥意思？ 其实也比较简单，就是前面虽然作者觉得通过重新定义损失，能够将模型的聚焦点放到更难训练的任务和样本上去，但是会不会网络本本身的结构也会影响到任务的优先级？ 作者想实验下，就给出了三种不同的模型架构：

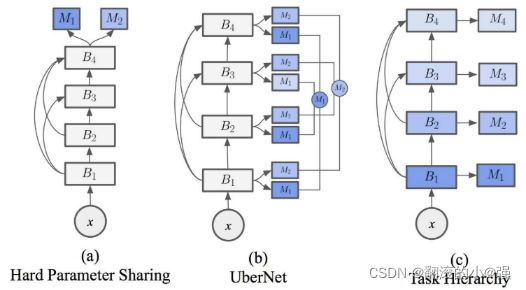
之前我们见过的大部分都是最左边这种结构，这种方式是所有任务都经过一个共享的底层，然后分开，各自训练自己的tower，总的来说就是并行训练。而task Hierarchy结构就是说，按照任务的难易程度划分，然后在share bottom里面，串行训练每个task，越简单的要放到最下面。

作者在这里做了一个实验，这里是4个任务，那么能够得到的排列组合就是$4!=24$种排列组合。接下来，对于每个任务，在task hierarchy结构中，会有4种不同的位置。在每个位置上，作者都进行了实验，可视化了4个任务在不同位置上训练的难易程度：

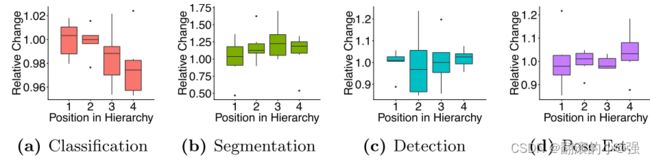
这里之所以是柱状图，是因为把一个任务固定到一个位置后，其他3个任务会有$3!$个排列组合，会有这么多次结果。所以通过上面图就会发现，c和d任务是比较难训练的，放到低层效果很差，需要更高层的共享特征。而a任务稍微简单。

所以作者根据任务的难易程度，分层级串行训练每个任务，结果发现要比其他两种效果好。

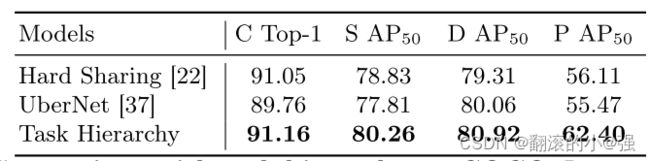
这说明，网络结构也会间接影响任务的优先级。所以如果不调整loss，调整网络结构也可能会使得效果提升。

把简单的任务放到低层，困难的任务放到高层，至于如何判断简单和困难，也可以像作者那样，随机排列组合，然后做一个评估指标的统计。

OK，这篇paper的精华内容我觉得梳理到这里差不多，如果还想了解更深的，可以看原paper，链接在底部。

6.3 代码实现

这里依然是基于之前的数据简单的把这个思路复现一下， 由于我并没有找到开源的这个思路代码，所以这里就按照自己的了解简单的实现了一下。但是这里由于一个分类任务一个回归任务，虽然整体能跑通，但结果不靠谱了。所以把这个思路放到带有回归的多任务上，我觉得应该是不行，或者可能我没有get到怎么实现这块吧。 如果多个任务，都是分类任务，我发现是可行的。

先放关键的思路代码，然后解释回归任务我这里为什么不可行：

我这里实现的时候，主要是两个点，一个是多个任务最终的loss计算，这里是利用了上面的DTP loss，所以这里需要改这个东西，而这个DTPloss，其实就是每个任务的Focal Loss与当前权重之和，只不过这里的权重是动态变化的，也是一个Focal计算。 所以这里的核心其实是Focal loss的实现，根据公式，我们可以写出二分类的Focal Loss计算公式：

# loss fuc这里需要自定义focal_loss
def focal_loss_binary(y_true, y_pred, gamma=2., alpha=.25):
    """
     Multi-labels Focal loss formula:
            FL = -alpha * (z-p)^gamma * log(p) -(1-alpha) * p^gamma * log(1-p)
                 ,which alpha = 0.25, gamma = 2, p = sigmoid(x), z = target_tensor.
    """
    # 这里是过滤，对于正样本，y_true等于1的位置保留y_pred，为0的地方置为1， 因为log1=0，负样本保留为0的地方，log1-0=0
    pt_1 = tf.where(tf.equal(y_true, 1), y_pred, tf.ones_like(y_pred))
    pt_0 = tf.where(tf.equal(y_true, 0), y_pred, tf.zeros_like(y_pred))
    
    return  -K.mean(alpha * K.pow(1.-pt_1, gamma) * K.log(pt_1+K.epsilon())) - K.mean((1-alpha) * K.pow(pt_0, gamma) * K.log(1.-pt_0+K.epsilon()))

def focal_loss_reg(y_true, y_pred, gamma=2.):
    
    mse = 1 / 2 * K.pow(y_true-y_pred, 2)
    # 保证在0-1之间
    mse = tf.nn.sigmoid(mse)
    return -K.mean(K.pow(1.-mse, gamma) * K.log(mse))

def focal_task_weight(k, r):
    # 保证在0-1之间
    k = tf.nn.sigmoid(k)
    return -K.pow(1-k, r) * K.log(k)

loss_func = {"binary": focal_loss_binary, "regression": focal_loss_reg}

我这里起初是实现了三个，一个是分类的，一个是回归的，一个是计算权重时候用的。按照论文里面说的，回归的和计算权重的我都加了sigmoid,因为得保证是0-1之间嘛。 但这么玩其实并不work。训练函数如下：

epochs = 2
batch_nums = math.ceil(train_data.shape[0] / batch_size)

task_types = ["regression", "binary"]
task_weight = [1.0, 1.0]
task_gamma = [1.0, 1.0]

for epoch in tqdm(range(epochs)):
    
    train_loss.reset_states()
    train_reg_loss.reset_states()
    train_bin_loss.reset_states()

    for feature, labels in train_ds:
        loss, loss_reg, loss_bin = train_step(feature, labels, task_types, task_weight)
    
    # 更新task weight FL(kt,rt)
    task_weight = [focal_task_weight(train_reg_loss.result(), task_gamma[0]), focal_task_weight(train_bin_loss.result(), task_gamma[1])]

    template = 'Epoch {}, Loss: {} - regression_loss: {} - binary_loss:{}, loss_weight: {}-{}'
    print(template.format(epoch, train_loss.result(), 
                          train_reg_loss.result(),
                          train_bin_loss.result(), task_weight[0], task_weight[1]))

这里我做的尝试就是把回归的这个任务值通过归一化操作弄到了0-1之间，因为这个时长原来是上百的数量级，直接计算Focal考虑到肯定有问题，所以转换了一下，然后去计算损失。 But，这样计算还是会出问题。关键就是sigmoid那里的操作，因为归一化之后，就成了非常接近0的一些数了，经过sigmoid，然后再Focal loss计算，就会出问题。

所以本身这个问题我就觉得不靠谱了，就此打住。然后给我的感觉，带有回归的任务，这个Focal loss不好计算，最好是别用。当然，如果有work的，麻烦告诉我一声呀。 如果多个二分类任务，这个思路是work的，把上面权重更新计算那里sigmoid去掉。 二分类任务能正常训练。

关于DTP的探索就到这里，总结下：

• 优点： 只需要获取不同step的KPI值，不需要获取不同任务的梯度，运算较快
• 缺点： 同样没有考虑不同任务的loss量级，需要额外操作把各个任务量级调整到差不多

7. Multi-task learning using uncertainty to weigh losses

这是2018年发表在CVPR上的一篇paper《 Multi-task learning using uncertainty to weigh losses for scene geometry and semantics》， 这里面的思路正好和上一篇相反，这里是希望让"简单"的任务有更高的权重。

当然，这里的简单并不是我们理解的简单，这个简单的衡量标准是"噪声少"， 这篇paper里面的思路是基于任务的不确定性去给每个任务加权，采用了概率建模的思路，希望噪声少确定性高的任务有更高的权重。

前面的引言和相关工作就不说了，基本上还是谈论到多任务联合建模的时候，loss权重很重要且模型对这个东西很敏感，还做了详细的实验证明这个问题。这里的多任务和之前的类似：

下面的核心问题，就是如何通过概率的思路建模每个任务，又是如何根据任务的不确定性调整每个任务权重的？但是在说这个之前，还是先了解贝叶斯建模的一些知识：

在贝叶斯建模中，有两种不同类型的不确定性可以建模:

• 认知不确定性(Epistemic uncertainty): 这个是模型中场景的一种不确定性，通常是数据不足产生的，可以通过增加训练数据来解释，认知不确定衡量的，是我们的输入数据是否在于已经见过的数据分布之中。
• 偶然不确定性(Aleatoric uncertainty): 捕捉到的是数据不能解释的信息，可以通过观测所有精度在提升的可解释变量来进行解释。这个又可以再分为两个子类：
  • 数据依赖性(异质方差Heteroscedastic): 是一种依赖于输入数据的偶然不确定性，可以用一个模型的输出预测。
  • 任务依赖性(同质方差Homoscedastic): 是不依赖于输入数据的偶然不确定性，它不是一个模型输出，而是一个对所有输入数据保持不变的量，并在不同的任务之间变化。因此，这东西可以描述任务之间的依赖关系。
    

这是论文里面给出的知识铺垫，但是我看到这里对同质和异质方差并不是很理解啥意思，于是乎简单搜了一个通俗的解释，放到这里，然后再说我对上面同质方差的理解。

假设有一个计量模型: $income=w\ast education+e$，描述了受教育水平和收入之间的关系，其中$e$为残差。

如果用最小二乘法对这种模型进行参数估计的时候，基于的一个假设就是$e$和任何变量都相互独立，即$E(e|x)=0$。 如果残差$e$与$x$相关了，那么此时残差$e$的方差会随着$x$变动而变动，此时方差是异质性的，称为异质性方差问题。

异方差问题导致什么问题？ 拿上面例子，一般来说受教育水平越高的人收入变动越大，而教育水平较低的人收入相差不大，此时就出现异方差问题，$e$的方差会随着教育水平$x$的增大而增大。

有了这个理解之后呢？我们再看多任务问题，多个任务共享了相同的收入，而对于每个任务的输出，其实都是一个基于噪声共享输入的条件概率函数。之所以作者要基于同质性方差来衡量任务的不确定性，就是要保证各个任务的这个噪声不要受到输入的干扰，只和任务本身有关。所以，我觉得这是这种方法的理论依据。

如果这个噪声受输入的干扰，那么多个任务之间的这个东西就没有可比性了，有差距也不知道是任务带来的还是输入造成了了，那么下面利用这种不确定给loss加权就不成立了。

OK， 那么有了理论依据，下面的思路就比较简单了。

7.1 Multi-task likelihoods

所谓概率建模思路，即使假定模型的输出是符合某项分布的，比如我们的回归问题，可以用一个高斯分布来定义我们的网络输出：

$$p\left(\mathbf{y}\mid {\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\right)=\mathcal{N}\left({\mathbf{f}}^{\mathbf{W}}(\mathbf{x}),{\sigma }^2\right)$$
这里的${\mathbf{f}}^{\mathbf{W}}(\mathbf{x})$可以理解成共享层最后的输出，${\mathbf{f}}^{\mathbf{W}}$是带有参数的神经网络函数。这个式子就是说我们的回归任务的最终输出可以建模成一个以${\mathbf{f}}^{\mathbf{W}}$为均值，${\sigma }^2$是方差的一个高斯分布。这里的${\sigma }^2$表示的当前任务的随机噪声(残差项)。

同理，对于分类任务，我们也可以按照这样的方式建模输出：
$$p\left(\mathbf{y}\mid {\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\right)=\mathrm{Softmax}\left({\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\right)$$
如果加入随机噪声的话，那么就是下面的
$$p\left(\mathbf{y}\mid {\mathbf{f}}^{\mathbf{W}}(\mathbf{x}),\sigma \right)=\mathrm{Softmax}\left(\frac{1}{{\sigma }^2}{\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\right)$$

当然，这是一个回归和分类任务表示，我们对于每一个都分别往后再走一步，写出他们的log likelihood:

1. 对于回归任务：
   $$\log p\left(\mathbf{y}\mid {\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\right)\propto -\frac{1}{2{\sigma }^2}{\Vert \mathbf{y}-{\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\Vert }^2-\log \sigma$$
   这个是什么鬼？ 其实就是把回归的正态分布的概率密度函数写出来化简，然后把$log\frac{1}{\sqrt{(2\pi )}}$这个东西约掉得到的，因为这是个常数，感兴趣的可以试一下。
   
2. 对于分类任务
   $$\begin{array}{rl}\log p\left(\mathbf{y}=c\mid {\mathbf{f}}^{\mathbf{W}}(\mathbf{x}),\sigma \right)& =\frac{1}{{\sigma }^2}{f}_c^{\mathbf{W}}(\mathbf{x})-\log \sum _{c^{\prime }}\exp \left(\frac{1}{{\sigma }^2}{f}_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right)\end{array}$$
   这个就是把softmax写出来，然后取对数化简得到的。

对于每个单任务，最终我们都想最大化他们的log似然函数，而取出参数$W$和噪声$\sigma$。

如果是多个任务联合建模呢？

这个式子理解下的话，联合概率相当于每个任务单独建模的概率乘积，为啥？ 这些任务相互独立？

虽然有疑问，但是想想我们的shared bottom模型，底层共享了shared bottom得到公共输出，然后去了各个任务独自的tower里面，得到每个任务最终的输出。

这个过程中，shared bottom的输出就类似于我们的$f^w(x)$，而各自塔里面的输出，就类似于我们上面说的随机噪声，而这个噪声和共享输入是相互独立的，只和任务本身有关。

这么考虑的话，上面这个式子是不是就合理了呢？ 并且我发现cv里面的大部分模型还真都是hard share bottom形式的，至于像soft shared(MMOE)这种，虽然可能也都在使用这种策略和思路，但背后基于的假设可能已经不成立了。 因为那个每个tower得到的共享输入是不同的专家组合，本质上$f^w(x)$变了，此时随机噪声就分不清是任务带来的还是这个输入带来的了。 Whatever, 有用就是王道!

有了上面的这个等式，我们就可以用概率的方式去建模多个任务了。

比如，如果是两个回归任务的话，根据上面化简：
$$\begin{array}{rl}p\left({\mathbf{y}}_1,{\mathbf{y}}_2\mid {\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\right)& =p\left({\mathbf{y}}_1\mid {\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\right)\cdot p\left({\mathbf{y}}_2\mid {\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\right)\\ & =\mathcal{N}\left({\mathbf{y}}_1;{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}),{\sigma }_1^2\right)\cdot \mathcal{N}\left({\mathbf{y}}_2;{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}),{\sigma }_2^2\right).\end{array}$$
我们的目标是最大化这个， 为了简化运算，往往这个会化简成最小化log似然，于是乎就得到了损失函数：
$$\begin{array}{rl}\mathcal{L}(\mathbf{W},{\sigma }_1,{\sigma }_2)& =-\log p\left({\mathbf{y}}_1,{\mathbf{y}}_2\mid {\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\right)\\ & \propto \frac{1}{2{\sigma }_1^2}{\Vert {\mathbf{y}}_1-{\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\Vert }^2+\frac{1}{2{\sigma }_2^2}{\Vert {\mathbf{y}}_2-{\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\Vert }^2+\log {\sigma }_1{\sigma }_2\\ & =\frac{1}{2{\sigma }_1^2}{\mathcal{L}}_1(\mathbf{W})+\frac{1}{2{\sigma }_2^2}{\mathcal{L}}_2(\mathbf{W})+\log {\sigma }_1{\sigma }_2\end{array}$$
这个式子就是普通的化简了，这里就会发现，两个任务的损失前面都自动加了一个$\frac{1}{2{\sigma }^2}$，这个东西就可以看成loss的权重。我们说$\sigma$表示的当前任务的噪声项，如果这个东西越大，就说明当前任务不确定性越高，比较难预测，或者预测出的结果不可靠，所以在目标损失中对应权重就会降低低。反之，权重会升高。所以不确定加权的方法会聚焦确定性高，预测结果可靠的任务上。 最后一项是对噪声的一个限制，不能让他太大，起到了正则化的效果。

这个可能比较直观，下面看一个不太直观的，也就是一个分类一个回归的情况。
$$\begin{array}{rl}\mathcal{L}(\mathbf{W},{\sigma }_1,{\sigma }_2)& =-\log p\left({\mathbf{y}}_1,{\mathbf{y}}_2=c\mid {\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\right)\\ & =-\log \mathcal{N}\left({\mathbf{y}}_1;{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}),{\sigma }_1^2\right)\cdot \mathrm{Softmax}\left({\mathbf{y}}_2=c;{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}),{\sigma }_2\right)\\ & =\frac{1}{2{\sigma }_1^2}{\Vert {\mathbf{y}}_1-{\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\Vert }^2+\log {\sigma }_1-\log p\left({\mathbf{y}}_2=c\mid {\mathbf{f}}^{\mathbf{W}}(\mathbf{x}),{\sigma }_2\right)\\ & =\frac{1}{2{\sigma }_1^2}{\Vert {\mathbf{y}}_1-{\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\Vert }^2+\log {\sigma }_1-(\frac{1}{{\sigma }_2^2}{f}_c^{\mathbf{W}}(\mathbf{x})-\log \sum _{c^{\prime }}\exp \left(\frac{1}{{\sigma }_2^2}{f}_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right))\\ & =\frac{1}{2{\sigma }_1^2}{\Vert {\mathbf{y}}_1-{\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\Vert }^2+\log {\sigma }_1-(\frac{1}{{\sigma }_2^2}{f}_c^{\mathbf{W}}(\mathbf{x})-\frac{1}{{\sigma }_2^2}\log \sum _{c^{\prime }}\exp \left(f_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right)+\frac{1}{{\sigma }_2^2}\log \sum _{c^{\prime }}\exp \left(f_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right)-\log \sum _{c^{\prime }}\exp \left(\frac{1}{{\sigma }_2^2}{f}_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right))\\ & =\frac{1}{2{\sigma }_1^2}{\Vert {\mathbf{y}}_1-{\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\Vert }^2+\log {\sigma }_1-\frac{1}{{\sigma }_2^2}\left(f_c^{\mathbf{W}}(\mathbf{x})-\log \sum _{c^{\prime }}\exp \left(f_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right)\right)-\frac{1}{{\sigma }_2^2}\log \sum _{c^{\prime }}\exp \left(f_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right)+\log \sum _{c^{\prime }}\exp \left(\frac{1}{{\sigma }_2^2}{f}_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right)\\ & =\frac{1}{2{\sigma }_1^2}{\Vert {\mathbf{y}}_1-{\mathbf{f}}^{\mathbf{W}}(\mathbf{x})\Vert }^2+\log {\sigma }_1+\frac{1}{{\sigma }_2^2}(-logSoftmax(y_2,{\mathbf{f}}^{\mathbf{W}}(\mathbf{x})))+\log \sum _{c^{\prime }}\exp \left(\frac{1}{{\sigma }_2^2}{f}_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right)-\log \sum _{c^{\prime }}\exp {\left(f_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right)}^{\frac{1}{{\sigma }_2^2}}\\ & =\frac{1}{2{\sigma }_1^2}{\mathcal{L}}_1(\mathbf{W})+\frac{1}{2{\sigma }_1^2}{\mathcal{L}}_2(\mathbf{W})+\log {\sigma }_1+\log \frac{{\sum }_{c^{\prime }}\exp \left(\frac{1}{{\sigma }_2^2}{f}_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right)}{{\sum }_{c^{\prime }}\exp {\left(f_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right)}^{\frac{1}{{\sigma }_2^2}}}\\ & \approx \frac{1}{2{\sigma }_1^2}{\mathcal{L}}_1(\mathbf{W})+\frac{1}{{\sigma }_2^2}{\mathcal{L}}_2(\mathbf{W})+\log {\sigma }_1+\log {\sigma }_2\end{array}$$
这就是整个推导过程，论文里面这个地方不是很详细，我这里稍微展开了下。另外，最后这里之所以能够这么近似化简，是因为作者做了一个近似假设$\frac{1}{{\sigma }_2}{\sum }_{c^{\prime }}\exp \left(\frac{1}{{\sigma }_2^2}{f}_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right)\approx {\sum }_{c^{\prime }}\exp {\left(f_{c^{\prime }}^{\mathbf{W}}(\mathbf{x})\right)}^{\frac{1}{{\sigma }_2^2}}$，当${\sigma }_2$趋近1的时候，这个就成立了。

这时候就会发现依然是在每个损失前面自动加了个损失权重， 而回归和分类的区别无非是回归前面的权重分母上有个2而已。看到两个回归以及一个回归一个分类任务的组合loss之后，我想两个分类的也能够一下子写出来了吧。实现上的细节：

这个的意思就是令$s=log{\sigma }^2$，则:
$$2\times 上式\approx exp(-s_1)\times {\mathcal{L}}_1(\mathbf{W})+2exp(-s_2)\times {\mathcal{L}}_2(\mathbf{W})+s_1+s_2$$
代码实现的时候，用的是这个。其中${\mathcal{L}}_1$表示回归任务，${\mathcal{L}}_2$表示分类任务。

OK， 这就是这篇paper里面根据任务不确定性进行自适应加权的思路了。

7.2 代码实现

这个代码实现相对简单，在之前的基础上进行的思路复现，这个只需要修改train_step即可， 尝试了两种方案，一种是以epoch为单位进行更新权重的，这时候就需要把梯度回传到训练函数中，并且需要连续微分，计算的时候会贼慢。代码如下：

#@tf.function
def train_step(features, labels, task_types, weight):
    losses = []
    gnorms = []
    
    # RuntimeError: GradientTape.gradient can only be called once on non-persistent tapes
    # 这是因为GradientTape 占用的资源默认情况下dw = t.gradient(loss, w)计算完毕就会立即释放
    # 如果连续计算微分， 指定persistent=True
    with tf.GradientTape(persistent=True) as tape:
        # 遍历每个任务
        for i, task_type in enumerate(task_types):
            out = model(features, training=True)
            task_loss = loss_func[task_types[i]](out[i], labels[i])
            # print("task_loss", task_loss)
            if task_types[i] == "regression":
                losses.append(tf.math.exp(-1 * weight[i]) * task_loss + weight[i])
            elif task_types[i] == "binary":
                losses.append(2 * tf.math.exp(-1 * weight[i]) * task_loss + weight[i])
                
        # 这里更新
        loss = tf.add_n(losses)
        gradients = tape.gradient(loss, model.trainable_variables)
        
        # 求权重的梯度
        weight1_grad = tape.gradient(loss, weight[0])
        weight2_grad = tape.gradient(loss, weight[1])
        weight_grads = [weight1_grad, weight2_grad]
        
    # 更新所有W参数
    optimizer.apply_gradients(zip(gradients, model.trainable_variables))
    
    train_loss(loss)
    train_reg_loss(losses[0])
    train_bin_loss(losses[1])
    
    return loss, losses[0], losses[1], weight_grads

这里UML的具体实现，就是上面loss.append这里， 这里的weight直接是公式中的$s$。这种方式是有效果的，损失下降的还挺快。

第二种方式的话，以batch的维度更新权重参数，具体代码如下：

@tf.function
def train_step(features, labels, task_types, weight):
    losses = []
    gnorms = []
    
    # RuntimeError: GradientTape.gradient can only be called once on non-persistent tapes
    # 这是因为GradientTape 占用的资源默认情况下dw = t.gradient(loss, w)计算完毕就会立即释放
    # 如果连续计算微分， 指定persistent=True
    with tf.GradientTape() as tape:
        # 遍历每个任务
        for i, task_type in enumerate(task_types):
            out = model(features, training=True)
            task_loss = loss_func[task_types[i]](out[i], labels[i])
            # print("task_loss", task_loss)
            if task_types[i] == "regression":
                losses.append(tf.math.exp(-1 * weight[i]) * task_loss + weight[i])
            elif task_types[i] == "binary":
                losses.append(2 * tf.math.exp(-1 * weight[i]) * task_loss + weight[i])
                
        # 这里更新
        loss = tf.add_n(losses)
        gradients = tape.gradient(loss, model.trainable_variables+weight)
        
    # 更新所有W参数
    optimizer.apply_gradients(zip(gradients, model.trainable_variables+weight))
    
    train_loss(loss)
    train_reg_loss(losses[0])
    train_bin_loss(losses[1])
    
    return loss, losses[0], losses[1]

这个首先训练速度会快，不用连续求微分，另外就是效果比上面好太多。

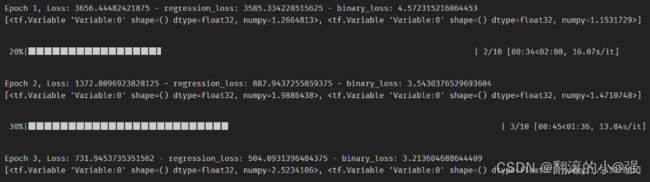
虽然实验做的很粗糙，但上面试了这么多方法，还就是这个给了我靠谱的感觉，既快又有效。感兴趣的可以试一下。

这个UML聚焦的是低噪声，确定性的任务，而DTP聚焦更难的任务，貌似这俩看起来有些相反，但不一定冲突，可能前者更适合于标签噪声更大的数据， 而DTP可能适合干净的数据。

小总

哇，花了大约一周的时间，终于把常见且比较经典的几种有关于多任务学习loss的优化方式进行了总结，篇幅很长(第一次破五万)，因为在整理的过程中，我喜欢把我自己的理解和思考记录下来，有时候还会进行一些知识的串联，所以可能会比较啰嗦，但还是希望在多任务loss优化方面能带给大家一些新思路和收获吧。

为了抓重点，下面对这四种loss优化的方式集中总结提炼下：

方法	动机	平衡loss量级	平衡学习速度	高权重任务	需要计算梯度	需要额外权重操作
GradNorm	平衡学习速度和loss量级	Yes	Yes		Yes
DWA	平衡学习速度		Yes			Yes
DTP	聚焦难学任务			困难的		Yes
UML	聚焦低噪声任务			噪声低的

这些优化方法与网络结构并不冲突，只要是多任务学习场景，都可以考虑这些loss优化的思路，所以这是通用性的东西。

另外，就是我上面针对每种思路都有尝试复现以及进行一些小实验，但这些实验都不能作为参考结果，因为做的很粗糙， 没有任何处理，还进行了采样等，只是想从代码层面看的细致一些。不具有权威性哈，感兴趣的可以拿自己真实的任务跑跑，然后对比试试效果哈。

参考

• Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks
• DWA: End-to-End Multi-Task Learning with Attention
• UWL: Multi-task learning using uncertainty to weigh losses for scene geometry and semantics
• DTP: Dynamic task prioritization for multitask learning
• 多目标学习优化
• 如何融合多任务学习 (Multi-Task Learning ) 损失函数loss
• Dynamic Task Prioritization for Multitask Learning方法

整理这篇文章的同时， 也建立了一个GitHub项目， 把各种主流的推荐模型复现一遍，并用通俗易懂的语言进行注释和逻辑整理， 模型大部分都介绍完了，接下来这个项目主要是代码方面的相关优化工作，比如数据集统一，实验统一， 模型复现代码完善以及增加pytorch版等。

今天的多loss优化设计相关代码已经上传， 该GitHub项目只是单纯供学习使用， 不作任何商业用途，感兴趣的可以看一下 ，star下我会更开心哈哈

筋斗云: https://github.com/zhongqiangwu960812/AI-RecommenderSystem