【刷题日记】笔试经典编程题目（四）

大家好，我是白晨，一个不是很能熬夜，但是也想日更的人✈。如果喜欢这篇文章，点个赞，关注一下白晨吧！你的支持就是我最大的动力！

前言

---

虽然还有很多课，但是也不能忘了写编程题呀。

白晨总结了大厂笔试时所出的经典题目，本周题型包括动态规划，条件控制，数学归纳，算法等，难度比上周基本持平，有些题目非常巧妙，都是很有代表性的经典题目，适合大家复习和积累经验。

这里是第四周，大家可以自己先试着自己挑战一下，再来看解析哟！

---

笔试经典编程题目(四)

---

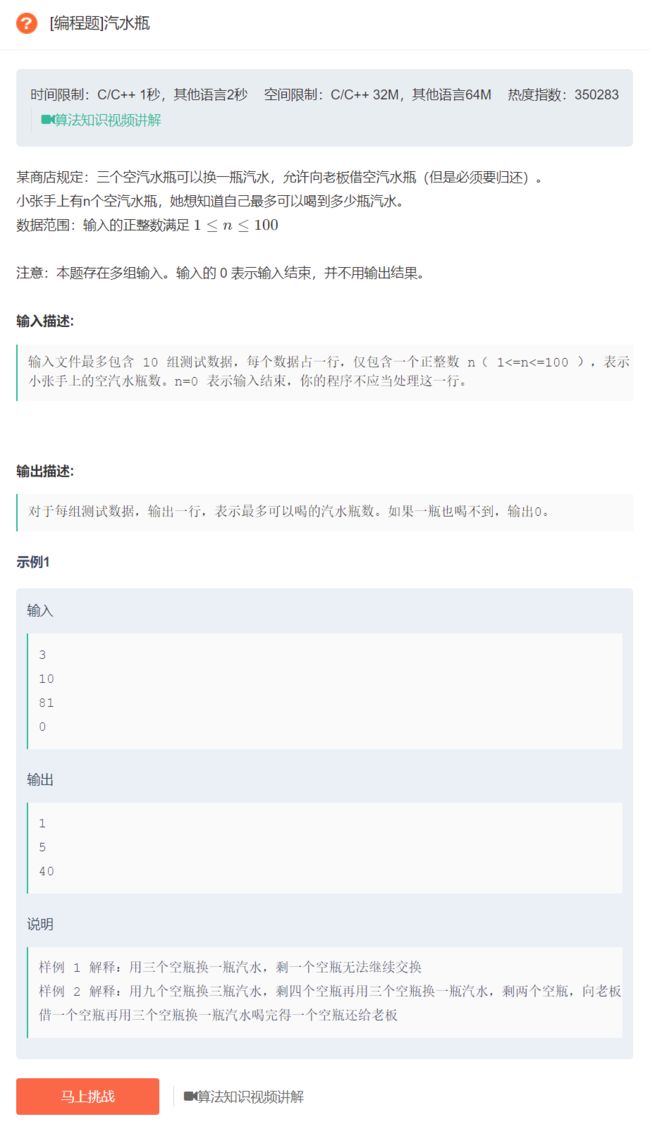
1.汽水瓶

---

原题链接：汽水瓶

• 法一：递归

算法思想：

• 根据题目的意思，喝三个汽水换一个瓶盖，并且还可以借瓶盖，借瓶盖是要还的，假设我们最后剩两个瓶盖，那么我们可以借一个瓶盖，换一瓶汽水，喝完以后还回去一个瓶盖，所以只有最后剩两个瓶盖时可以借一个瓶盖，少于两个不能借瓶盖。

根据上面的思路写出递归方程：

⚔ 代码实现：

#include 
using namespace std;

int bottle(int num)
{
    // 少于两个瓶盖证明不能换汽水了，返回0
    if (num <= 1)
        return 0;
    // 两个瓶盖可以再换一瓶汽水
    else if (num == 2)
        return 1;
	// 当前瓶盖可以换的汽水数
    int cnt = num / 3;
    // 瓶盖剩余：num = num - 3 * cnt + cnt
    num -= 2 * cnt;
    return cnt + bottle(num);
}

int main()
{
    int num;
    while (cin >> num)
    {
        if (num == 0)
            return 0;
        int cnt = bottle(num);
        cout << cnt << endl;
    }
    return 0;
}

• 法二：找规律

算法思想：

• f(1) = 0

• f(2) = 1

• f(3) = 1

• f(4) = 2 //4个瓶子，其中3个可以换1瓶水+1个空瓶，所以是f(2)+1

• f(5) = 2 //3个瓶子换1瓶水+1个空瓶，所以是f(3)+1

• f(6) = 3

• f(7) = 3

• …

• f(n) = n / 2

所以，能换的汽水数就是 n / 2 个。

⚔ 代码实现：

#include 
using namespace std;

int main()
{
    int n;
    while (cin >> n)
    {
        if (n == 0)
            break;
        cout << n / 2 << endl;
    }
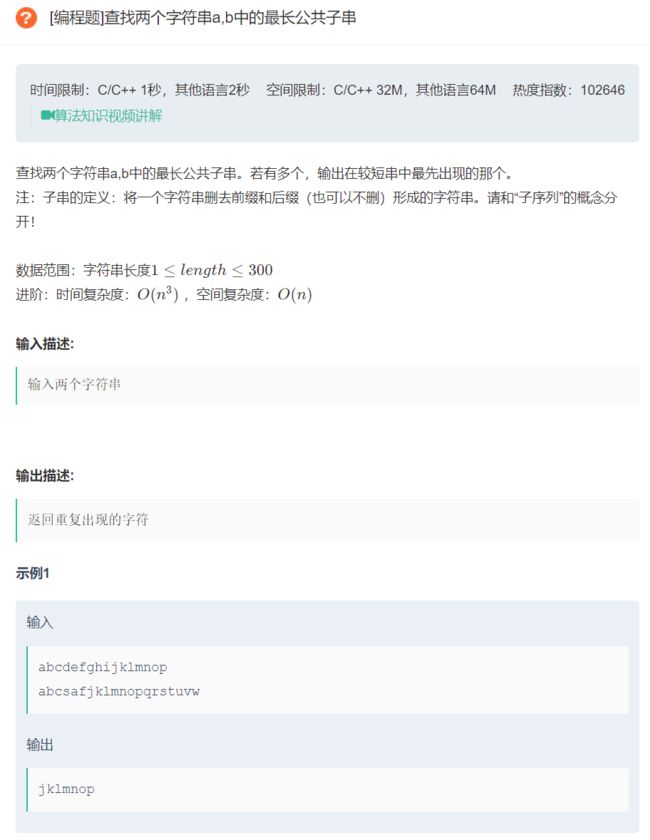
    return 0;
}

---

2.查找两个字符串a,b中的最长公共子串

---

原题链接：查找两个字符串a,b中的最长公共子串

• 法一：暴力求解

算法思想：

• 直接暴力实现，将较短的串依次拆解成若干个子串substr，一一在较长串中匹配。
• 如果匹配成功，并且此时substr的长度大于目前最长的公共子串，记录此时的substr
• 如果匹配失败，则此substr以及较短串中substr后的字符串不可能再匹配上。
• eg. 较短串a：abcde ，较长串b：abdddd， substr ：abc ，此时abc不能匹配长串中的部分串，证明abcd以及abcde也不能匹配长串。
• 不断拆分较短串，直到把所有情况都拆分匹配完毕。
• 时间复杂度：$O(N^4)$ ，

⚔ 代码实现：

#include 
#include 
#include 
using namespace std;

int main()
{
    string a, b;
    string max_str;
    cin >> a >> b;
    if (a.size() > b.size())
        swap(a, b);
	
    // i下标为此子串的起点
    for (int i = 0; i < a.size(); ++i)
    {
        // j下标为此子串的终点
        for (int j = i; j < a.size(); ++j)
        {
            string tmp = a.substr(i, j - i + 1);
            // 如果匹配不上，说明以i为起点的子串后续再也不能匹配上，直接跳出
            if (b.find(tmp) == -1)
                break;
            else if (tmp.size() > max_str.size())
                max_str = tmp;
        }
    }
    cout << max_str << endl;
    return 0;
}

• 法二：递动态规划

算法思想：

• 状态：dp[i][j] —— a[0 ~ i-1] 与 b[0 ~ j-1] 的最长公共子串。
• 初始化：$dp[0][i]=dp[0][j]=0$ ，下标为0代表空串，任何串和空串匹配最长公共字符串长度都为0。
• 状态转移方程：当a[i-1]==b[j-1]时，$dp[i][j]=dp[i-1][j-1]+1$ ，不相等时，逻辑上讲，此时最长公共串长度应该为dp[i-1][j-1]，但是为了方便处理，我们将其规定$dp[i][j]=0$。
• 返回值：用一个start变量记录最长公共串的初始位置，得到最长串的长度为len ，那么最长串就是a[start ~ start+len-1]。
• 时间复杂度：$O(N^3)$

eg.

a：cbcd ，b：abcde

	“”	a	b	c	d	e
“”	0	0	0	0	0	0
c	0	0	0	1	0	0
b	0	0	1	0	0	0
c	0	0	0	2	0	0
d	0	0	0	0	3	0

⚔ 代码实现：

#include 
#include 
#include 
using namespace std;

int main()
{
    string a, b;
    cin >> a >> b;
    // 将a设为较短串
    if (a.size() > b.size())
        swap(a, b);
    int m = a.size();
    int n = b.size();
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    int start = 0;
    int len = 0;

    for (int i = 1; i <= m; ++i)
    {
        for (int j = 1; j <= n; ++j)
        {
            if (a[i - 1] == b[j - 1])
            {
                dp[i][j] = dp[i - 1][j - 1] + 1;
                if (dp[i][j] > len)
                {
                    len = dp[i][j];
                    start = i - len;
                }
            }
        }
    }

    cout << a.substr(start, len) << endl;
    return 0;
}

优化意见：

题目中的最优空间复杂度是$O(N)$，说明我们空间上还没有做到最优。我们观察到，动态规划dp[i][j]只与dp[i-1][j-1]有关，所以我们只需要前一行的前一个数据即可，我们可以用一维数组实现，具体实现可以自行尝试。

---

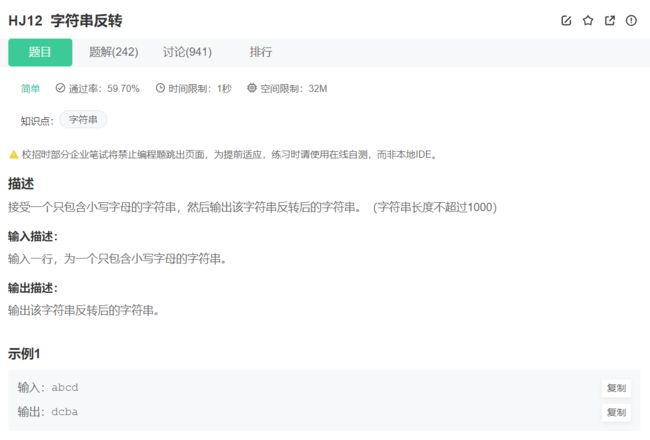
3.字符串反转

---

原题链接：字符串反转

算法思想：

这个题没有什么好说的，直接反转就可以，无论用双指针还是直接调用函数。

⚔ 代码实现：

#include 
#include 
#include 
using namespace std;

int main()
{
    string s;
    cin >> s;
    reverse(s.begin(), s.end());
    cout << s << endl;
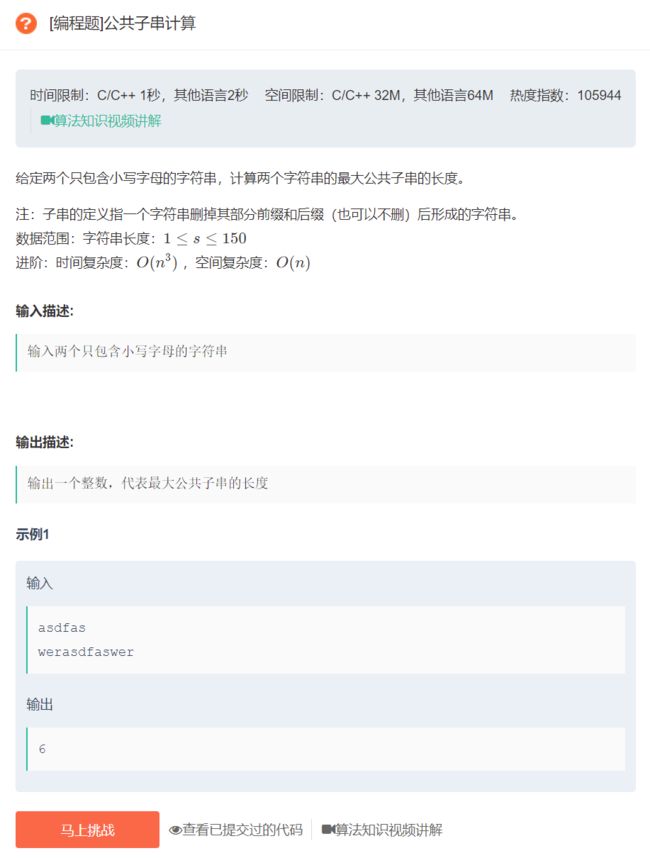
    return 0;
}

---

4.公共子串计算

---

原题链接：公共子串计算

算法思想：

同第二题：点击跳转

⚔ 代码实现：

#include 
#include 
#include 
using namespace std;

int main()
{
    string a, b;
    cin >> a >> b;
    // 将a设为较短串
    if (a.size() > b.size())
        swap(a, b);
    int m = a.size();
    int n = b.size();
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    int len = 0;

    for (int i = 1; i <= m; ++i)
    {
        for (int j = 1; j <= n; ++j)
        {
            if (a[i - 1] == b[n - j])
            {
                dp[i][j] = dp[i - 1][j - 1] + 1;
                if (dp[i][j] > len)
                {
                    len = dp[i][j];
                }
            }
        }
    }

    cout << len << endl;
    return 0;
}

---

5.洗牌

---

原题链接：洗牌

算法思想：

题目洗牌过程太花里胡哨了，其实我们直接看初始条件和最终条件的对比就可以得到洗牌的规律。

设当前手牌数组为v，初始条件数组为tmp，i=1~n，从上面的过程我们可以总结出来洗牌的规律：

• 当v下标为偶数时：$v[2\ast i]=tmp[i]$
• 当v下标为奇数时：$v[2\ast i+1]=tmp[i+n]$

⚔ 代码实现：

#include 
#include 
using namespace std;

int main()
{
    int T;
    cin >> T;
    while (T--)
    {
        int n, k;
        cin >> n >> k;
        vector<int> ans(2 * n);
        for (int i = 0; i < ans.size(); ++i)
            cin >> ans[i];
        // 洗k次牌
        while (k--)
        {
            // 初始条件
            vector<int> tmp(ans.begin(), ans.end());
            // 洗牌
            for (int i = 0; i < n; ++i)
            {
                ans[2 * i] = tmp[i];
                ans[2 * i + 1] = tmp[i + n];
            }
        }
        cout << ans[0];
        for (int i = 1; i < ans.size(); ++i)
            cout << " " << ans[i];
        cout << endl;
    }
    return 0;
}

---

6.MP3光标位置

---

原题链接：MP3光标位置

算法思想：

• 这个题算是牛客网条件给的最全的题目了，所以省去了很多分析时间，只需要按照题目条件进行分类即可。

• 具体条件控制见代码。

⚔ 代码实现：

#include 
#include 
using namespace std;

void Change(char mod, int& pos, int& top, int& bottom, int n)
{
    // 根据指令进行加减
    if (mod == 'D')
        pos += 1;
    else
        pos -= 1;
	// 单独处理最顶端位置向上翻和最低端位置向下翻的情况
    if (pos == 0)
    {
        pos = n;
        bottom = n;
        top = bottom - 3;
    }
    else if (pos == n + 1)
    {
        pos = 1;
        top = 1;
        bottom = top + 3;
    }
    else
    {
        // 当显示的歌曲已经超出屏幕显示的歌曲范围时，更改歌曲的范围
        if (pos == bottom + 1)
        {
            top++;
            bottom++;
        }
        else if (pos == top - 1)
        {
            top--;
            bottom--;
        }
        // 其余情况不用更改歌曲范围，我们不做处理
    }
}

int main()
{
    int n;
    string s;
    cin >> n >> s;
	
    // 小于等于四首歌时单独处理
    if (n <= 4)
    {        
        int pos = 1;// 当前行的歌曲，默认为1
        int top = 1;// 一页曲单的顶部
        // 此时最多显示n首歌
        int bottom = n;// 一页曲单的底部
        for (auto& ch : s)
        {
            if (ch == 'D')
                pos++;
            else
                pos--;
			// 单独处理最顶端位置向上翻和最低端位置向下翻的情况
            if (pos == 0)
                pos = n;
            else if (pos == n + 1)
                pos = 1;
            // 不用处理翻页歌曲显示范围
        }
        for (int i = top; i <= bottom; ++i)
            cout << i << " ";
        cout << endl << pos;
    }
    else
    {
        int pos = 1;// 当前行的歌曲，默认为1
        int top = 1;// 一页曲单的顶部，默认为1
        int bottom = 4;// 一页曲单的底部，n>4时，默认为4

        for (auto& ch : s)
        {
            // 处理命令
            Change(ch, pos, top, bottom, n);
        }
        for (int i = top; i <= bottom; ++i)
        {
            cout << i << " ";
        }
        cout << endl << pos;
    }
    return 0;
}

---

7.小易的升级之路

---

原题链接：小易的升级之路

算法思想：

• 根据题目条件得出能力值即可。
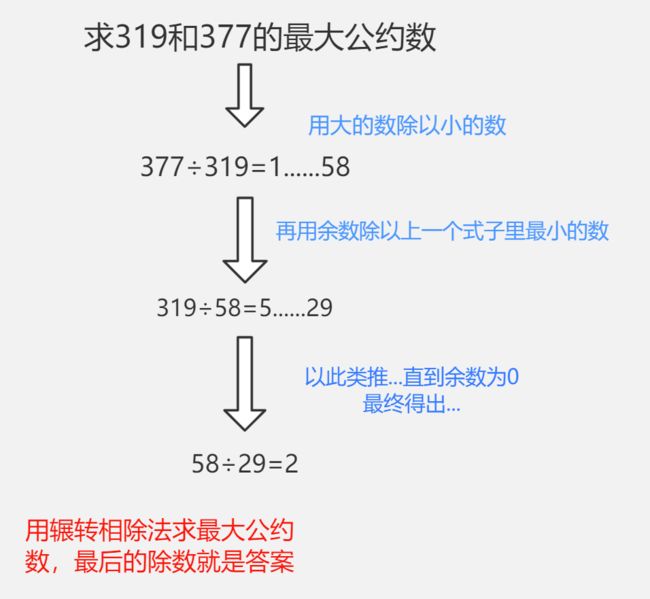
• 最小公倍数求法：

辗转相除法：

具体实例:

• ans = a * b / c

最小公倍数流程图：

所以，最小公倍数的代码实现为：

int getApp(int a, int b)
{
    int c;
    while(c = a % b)
    {
        a = b;
        b = c;
    }
    return b;
}

⚔ 代码实现：

#include 
#include 
using namespace std;

int getApp(int a, int b)
{
    int c;
    while(c = a % b)
    {
        a = b;
        b = c;
    }
    return b;
}

int main()
{
    int n, capa;
    while(cin >> n >> capa)
    {
        vector<int> v(n);
        for(int i = 0; i < n; ++i)
            cin >> v[i];
        for(int& e : v)
        {
            if(e <= capa)
                capa += e;
            else
                capa += getApp(capa, e);
        }
        cout << capa << endl;
    }
    return 0;
}

---

8.找出字符串中第一个只出现一次的字符

---

原题链接：找出字符串中第一个只出现一次的字符

算法思想：

• 哈希表思路，将出现的字母次数统计一遍。
• 最后遍历哈希表，找出只出现过一次的数字。

⚔ 代码实现：

#include 
#include 
using namespace std;

int main()
{
    string s;

    while (cin >> s)
    {
        int num[128] = { 0 };
        int flag = 1;
        for (auto ch : s)
        {
            num[ch]++;
        }

        for (auto ch : s)
        {
            if (num[ch] == 1)
            {
                flag = 0;
                cout << ch << endl;
                break;
            }
        }
        if (flag == 1)
            cout << -1 << endl;
    }

    return 0;
}

---

9.微信红包

---

原题链接：微信红包

算法思想：

• 这个题是数组中出现次数超过一半的数字的变式题目，所以我先将原题目解法贴在下方：

法一：哈希表

题目给出了传入数组的取值和长度，那么直接哈希就完事了，反正哈希表是定长的，遍历是常数，时间复杂度还是 $O(n)$ （bushi）。

static int cnt[10001] = { 0 };
class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        int len = numbers.size();
        for (auto e : numbers)
        {
            cnt[e]++;
        }

        for (int i = 0; i < 10001; i++)
        {
            if (cnt[i] > len / 2)
            {
                return i;
            }
        }

        return -1;
    }
};

法二：同归于尽法

虽然上一个方法可以run过去，但是时间是绝对长了，不一定符合 $O(n)$ ，对上一个方法存在质疑的同学可以看这个方法。

这个数组有一个数据出现超过了数组长度的一半，并且测试用例绝对是有答案的，所以就有了同归于尽法。

• 第一个数字作为第一个士兵，守阵地；count = 1；
• 遇到相同元素，count++;
• 遇到不相同元素，即为敌人，同归于尽,count–；当遇到count为0的情况，又以新的 i 值作为守阵地的士兵，继续下去，到最后还留在阵地上的士兵，有可能是主元素。
• 再加一次循环，记录这个士兵的个数看是否大于数组一般即可。

法二来自牛客网网友的分享

具体实现：

class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        int cnt = 0;
        size_t len = numbers.size();
        // 选择第一个数字当士兵
        int num = numbers[0];
        if (len == 1)
        {
            return numbers[0];
        }

        for (int i = 0; i < len; ++i)
        {
            // cnt==0，换士兵
            if (cnt == 0)
            {
                num = numbers[i];
            }
            
            if (numbers[i] == num)
            {
                ++cnt;
            }
            else
            {
                --cnt;
            }
        }

        return num;
    }
};

• 对比两个题目，我们可以得到微信红包这个题目是没有保证一定有一个数满足出现次数大于数组的一半，所以，最后得到的数还得再验证一下。
• ⚔ 代码实现：

#include 
#include 
#include 
using namespace std;

class Gift {
public:
    int getValue(vector<int> gifts, int n) {
        int cnt = 0;
        int num = 0;

        for (int& e : gifts)
        {
            if (cnt == 0)
            {
                num = e;
                cnt++;
            }
            else if (num == e)
            {
                cnt++;
            }
            else
            {
                cnt--;
            }
        }
        // 判断这个数有没有出现
        int i = 0;
        for (int& e : gifts)
        {
            if (num == e)
                i++;
        }
        if (i > n / 2)
            return num;
        else
            return 0;
    }
};

---

10.编辑距离

---

原题链接：编辑距离

算法思想：

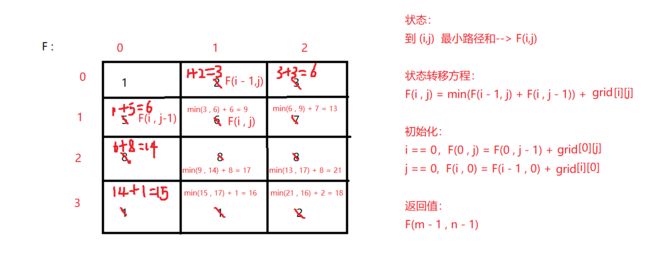
状态：

word1 的前 1，2，3，...m 个字符转换成 word2 的前 1，2，3，...n 个字符需要的编辑距离

• $F(i,j)$: word1 的前 i 个字符于 word2 的前 j 个字符的编辑距离

状态递推：

• $F(i,j)=minF(i-1,j)+1,F(i,j-1)+1,F(i-1,j-1)+(w1[i]==w2[j]?0:1)$

上式表示从删除，增加和替换操作中选择一个最小操作数

• $F(i-1,j)$: $w1[1,...,i-1]$ 于 $w2[1,...,j]$ 的编辑距离，删除 $w1[i]$ 的字符—> $F(i,j)$
• $F(i,j-1)$: $w1[1,...,i]$ 于 $w2[1,...,j-1]$ 的编辑距离，增加一个字符—> $F(i,j)$
• $F(i-1,j-1)$: $w1[1,...,i-1]$ 于 $w2[1,...,j-1]$ 的编辑距离，如果 $w1[i]$ 与 $w2[j]$ 相同，不做任何操作，编辑距离不变，如果 $w1[i]$ 与 $w2[j]$ 不同，替换 $w1[i]$ 的字符为 $w2[j]$—> $F(i,j)$

初始化：
初始化一定要是确定的值，如果这里加入空字符串，以便于确定初始化状态

• $F(i,0)=i$ :word与空串的编辑距离，删除操作
• $F(0,i)=i$ :空串与word的编辑距离，增加操作

返回结果：$F(m,n) $

⚔ 代码实现：

class Solution {
public:
    int minDistance(string word1, string word2) {
        if (word1.empty() || word2.empty())
            return max(word1.size(), word2.size());

        int len1 = word1.size();
        int len2 = word2.size();
        vector<vector<int>> ret(len1 + 1, vector<int>(len2 + 1, 0));

        // 初始化
        // j == 0 时
        for (int i = 0; i <= len1; ++i)
            ret[i][0] = i;
        // i == 0 时
        for (int i = 0; i <= len2; ++i)
            ret[0][i] = i;

        for (int i = 1; i <= len1; ++i)
        {
            for (int j = 1; j <= len2; ++j)
            {
                // 先选择删除 or 插入
                ret[i][j] = min(ret[i - 1][j] + 1, ret[i][j - 1] + 1);
				
                // 判断是否要替换，如果要替换，操作数 +1 ，反之不变
                // word1的第 i 个字符，对应索引为i - 1，word2同理
                if (word1[i - 1] == word2[j - 1])
                    ret[i][j] = min(ret[i - 1][j - 1], ret[i][j]);
                else
                    ret[i][j] = min(ret[i - 1][j - 1] + 1, ret[i][j]);
            }
        }

        return ret[len1][len2];
    }
};

---

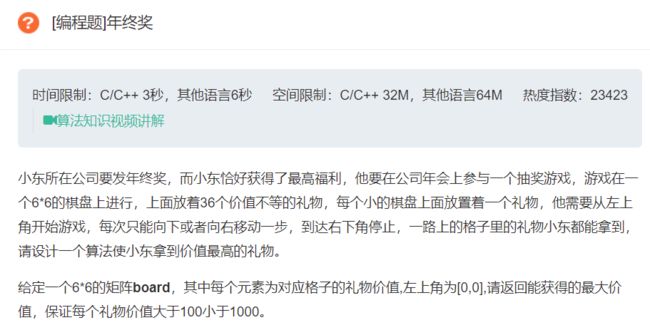
☕11.年终奖

---

原题链接：年终奖

算法思想：

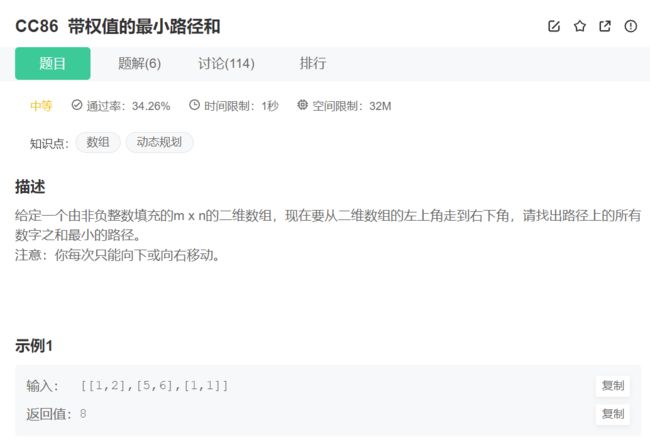
• 这就是一道非常经典的动态规划题目的变式，原题目是——带权值的最小路径和，以下是原题目的讲解：

原题链接：带权值的最小路径和

• 代码实现：

class Solution {
public:
    int minPathSum(vector<vector<int> >& grid) {
        int m = grid.size();
        int n = grid[0].size();
		
        //初始化
        for (int i = 1; i < m; i++)
            grid[i][0] = grid[i - 1][0] + grid[i][0];

        for (int i = 1; i < n; i++)
            grid[0][i] = grid[0][i - 1] + grid[0][i];
		
        // 转移方程
        for (int i = 1; i < m; i++)
        {
            for (int j = 1; j < n; j++)
                grid[i][j] = min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j];
        }

        return grid[m - 1][n - 1];
    }
};

• 年终奖这个题目比带权路径和还要简单，如果你能看明白上面的题解，相信也不难写出这道题。

⚔ 代码实现：

class Bonus {
public:
    int getMost(vector<vector<int> > board) {
        vector<vector<int>> dp(board.size(), vector<int>(board[0].size()));
        dp[0][0] = board[0][0];
        for (int i = 1; i < board.size(); ++i)
            dp[i][0] = board[i][0] + dp[i - 1][0];
        for (int j = 1; j < board[0].size(); ++j)
            dp[0][j] = board[0][j] + dp[0][j - 1];

        for (int i = 1; i < board.size(); ++i)
        {
            for (int j = 1; j < board[0].size(); ++j)
            {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + board[i][j];
            }
        }
        return dp[board.size() - 1][board[0].size() - 1];
    }
};

我们可以优化一下空间复杂度，直接使用原来的矩阵：

class Bonus {
public:
    int getMost(vector<vector<int> > board) {
        for (int i = 1; i < board.size(); ++i)
            board[i][0] = board[i][0] + board[i - 1][0];
        for (int j = 1; j < board[0].size(); ++j)
            board[0][j] = board[0][j] + board[0][j - 1];

        for (int i = 1; i < board.size(); ++i)
        {
            for (int j = 1; j < board[0].size(); ++j)
            {
                board[i][j] = max(board[i - 1][j], board[i][j - 1]) + board[i][j];
            }
        }
        return board[board.size() - 1][board[0].size() - 1];
    }
};

---

12.迷宫问题

---

原题链接：迷宫问题

算法思想：

• 经典的 深度优先搜索（DFS） 题目，如果没有见过这类题型的同学呢，可以跳转到【刷题日记】回溯算法(深度优先搜索)经典题目了解一下这类习题哟！

• 由于要打印出路径，所以我们必须创建一个字符串数组vs，让其随DFS函数不断变化，保存各个路径的信息。

• 如何实现DFS呢？

  • 首先，从一个点Q出发，我们需要遍历这个点周围上下左右的点，找到标记为0的点P就向P移动，进入下一个DFS，反之，找到标记为1的点就原地不动，继续查找。
  • 当然要注意，Q的上下左右的坐标不能越界！
  • 当Q的上下左右全部查找完，如果没有找到合适的路，回溯到上一个点；
  • 如果找到了路径，那么直接返回。

• 这里要特别注意的是，对于现在vs上的点，我们需要进行标记，防止走回头路，导致无限递归。

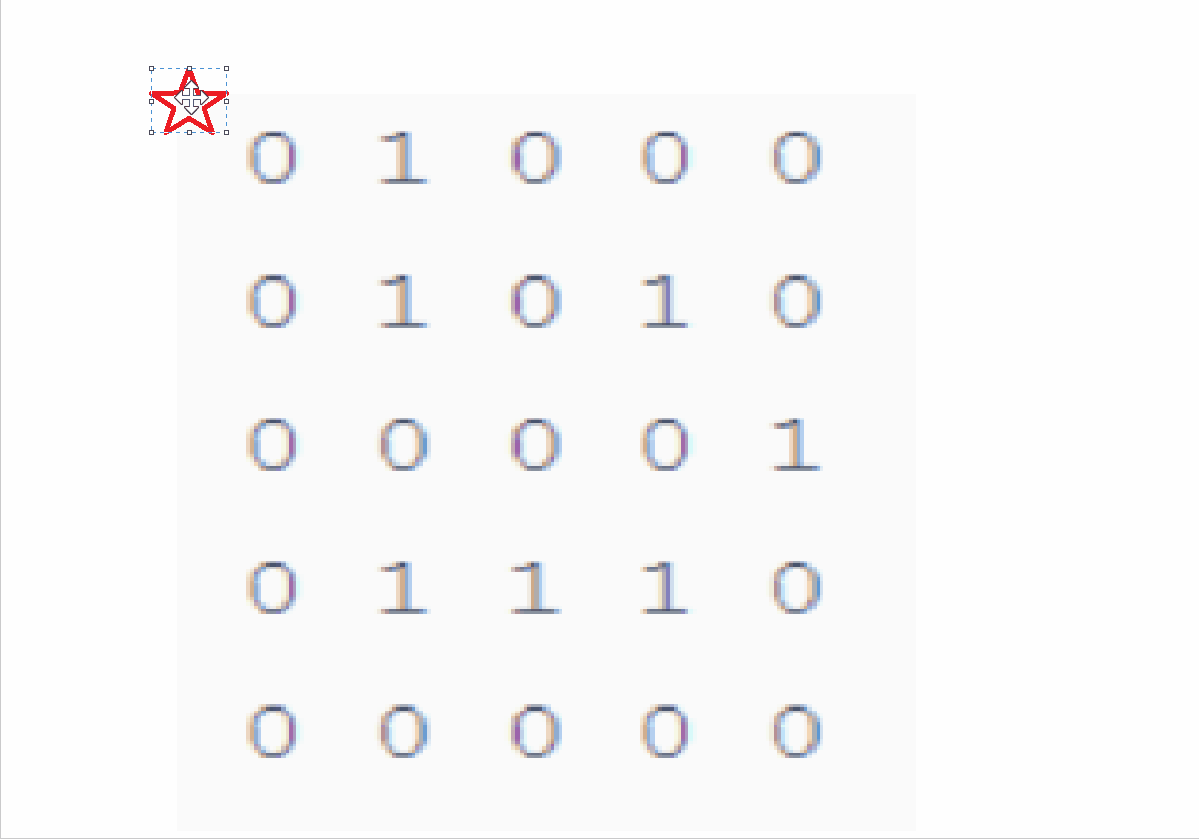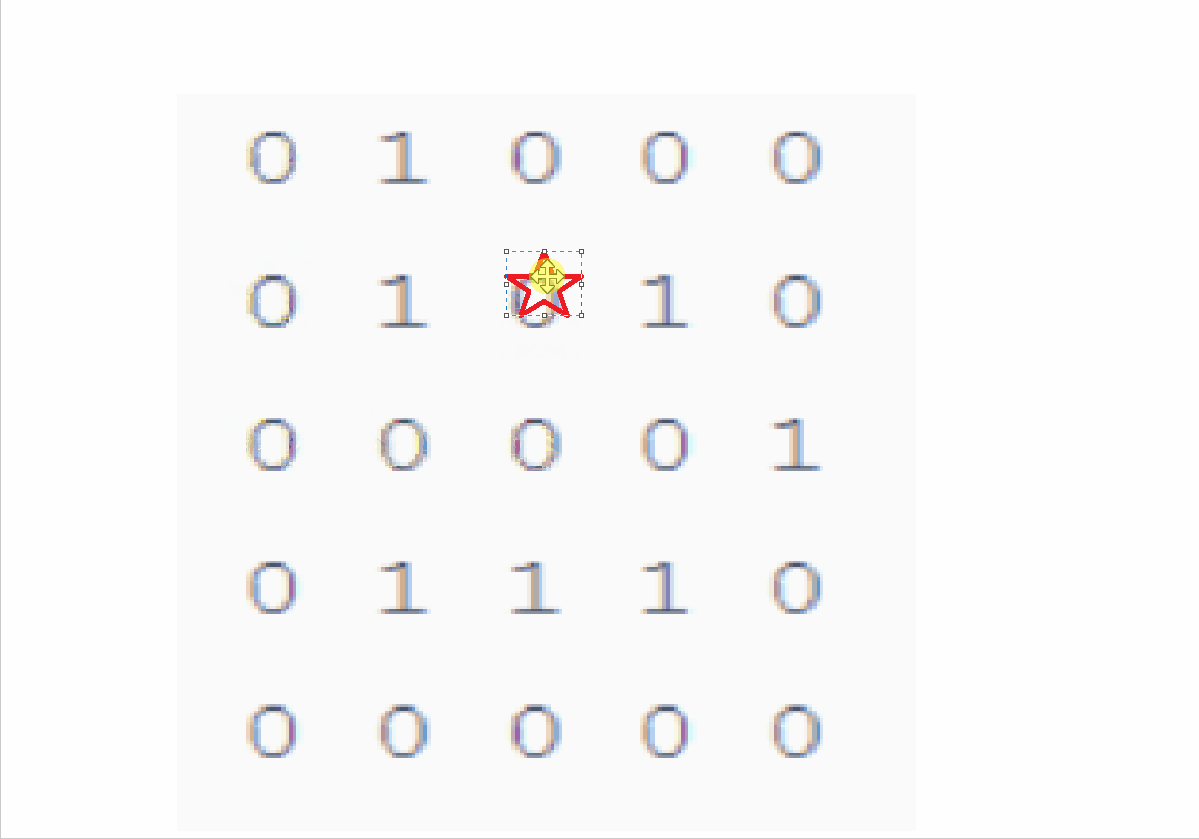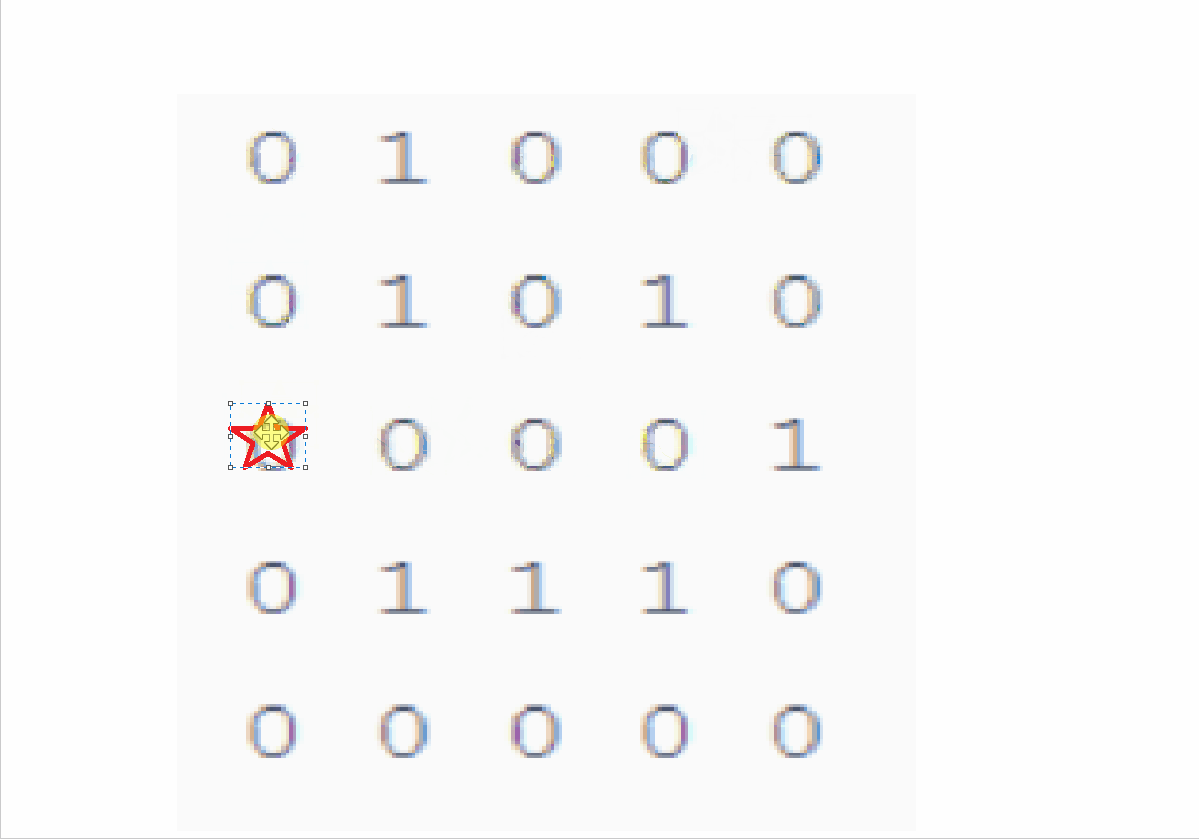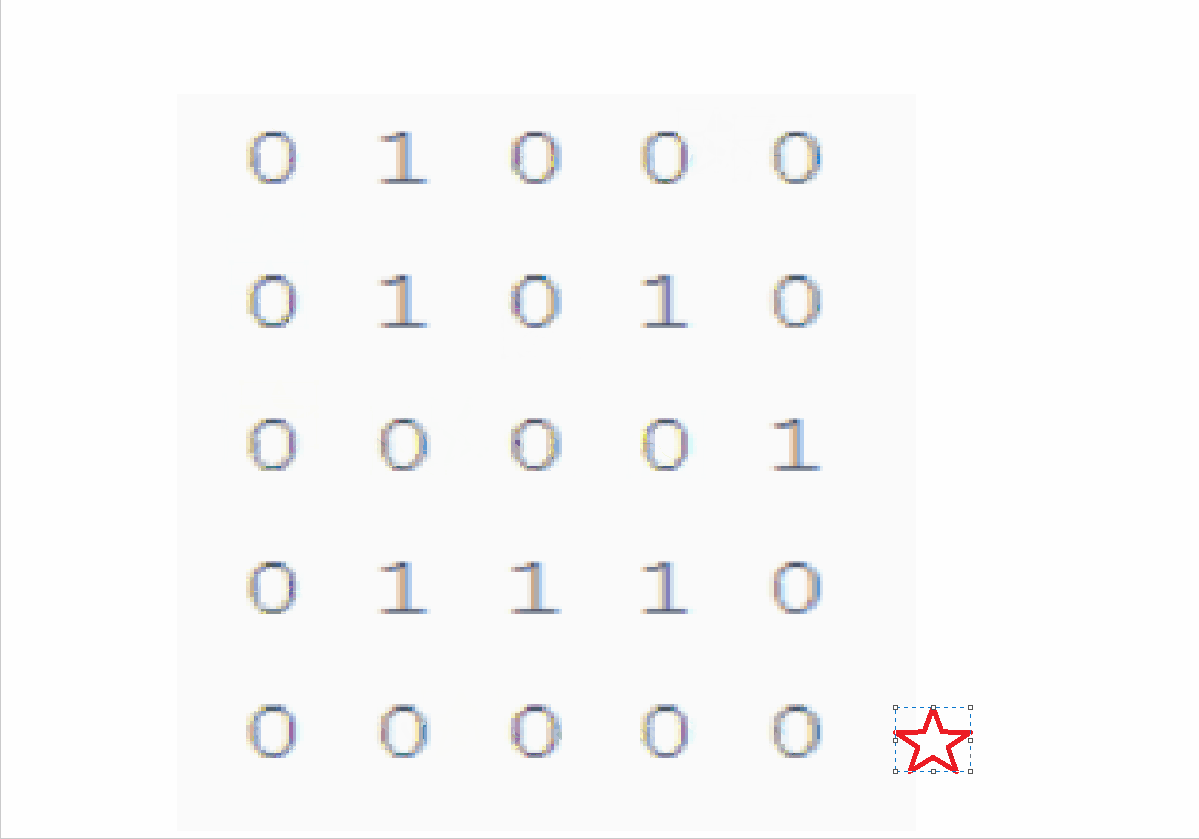
具体DFS过程见下图：

⚔ 代码实现：

#include 
#include 
#include 
using namespace std;
// 遍历的四个方向
static int des[4][2] = { {1, 0}, {-1, 0}, {0, 1}, {0, -1} };

void Dfs(vector<vector<int>>& v, vector<string>& vs, int row, int col, int i, int j, int& flag)
{
    // 将此点加入到vs中
    string tmp = "(";
    tmp += i + '0';
    tmp += ',';
    tmp += j + '0';
    tmp += ")";
    vs.push_back(tmp);
    // 如果到了右下角的点，返回
    if (i == row - 1 && j == col - 1)
    {
        flag = 1;
        return;
    }
    // 将此点进行标记，防止走回头路
    v[i][j] = 2;
    // 四个方向遍历
    for (int k = 0; k < 4; ++k)
    {
        int newi = i + des[k][0];
        int newj = j + des[k][1];
		// 检查是否越界
        if (newi < 0 || newj < 0 || newi >= row || newj >= col)
            continue;
        // 当遍历点可以走
        if (v[newi][newj] == 0)
            Dfs(v, vs, row, col, newi, newj, flag);
        // 找到路径，直接返回
        if (flag == 1)
            return;
    }
    // 遍历完仍没有找到路，说明此路不通，将其标记恢复
    v[i][j] = 0;
    // 舍去路径中的此点
    vs.pop_back();
}

int main()
{
    int m, n;
    cin >> m >> n;
    vector<vector<int>> v(m, vector<int>(n));
    vector<string> vs;
    for (int i = 0; i < v.size(); ++i)
    {
        for (int j = 0; j < v[0].size(); ++j)
        {
            cin >> v[i][j];
        }
    }
    int flag = 0;
    Dfs(v, vs, v.size(), v[0].size(), 0, 0, flag);
    for (auto& s : vs)
        cout << s << endl;
    return 0;
}

---

后记

---

本次题目难度没有太大波动，但是这次题目主要集中在动态规划和数学归纳这两个上限很高的题目，比较考验大家的逻辑以及代码思维，相信大家做完会有所收获。

这个是一个新的系列——《笔试经典编程题目》，隶属于【刷题日记】系列，白晨开这个系列的目的是向大家分享经典的笔试编程题，以便于大家参考，查漏补缺以及提高代码能力。如果你喜欢这个系列的话，不如关注白晨，更快看到更新呀。

本文是笔试经典编程题目的第四篇，如果喜欢这个系列的话，不如订阅【刷题日记】系列专栏，更快看到更新哟

---

如果解析有不对之处还请指正，我会尽快修改，多谢大家的包容。

如果大家喜欢这个系列，还请大家多多支持啦！

如果这篇文章有帮到你，还请给我一个大拇指 和小星星 ⭐️支持一下白晨吧！喜欢白晨【刷题日记】系列的话，不如关注白晨，以便看到最新更新哟！！！

我是不太能熬夜的白晨，我们下篇文章见。