人工智能算法_人工智能算法——用AO*算法求解一个智力难题

用AO*算法求解一个智力难题

本文节选自《人工智能习题解析与实践》

有这样一个智力问题：有12枚硬币，凡轻于或重于真币者，即为假币(只有一枚假币)，要设计一个搜索算法来识别假币并指出它是轻于还是重于真币，且利用天平的次数不多于3次。

利用人工智能的求解方法解决这个问题首先必须解决下面两个问题:

¨   问题表示方法，记录和描述问题的状态。

¨  求解程序如何对某种称法进行评价。

下面我们就对使用AO*算法求解这个智力难题进行讨论。

1．问题的表示

我们要分析：构成该问题状态的因素有那些；硬币可能有哪些状态；每称一次后，有关硬币的状态的会发生什么样的变化；天平每称一次后，必须保留所剩的使用天平的次数。

我们可将硬币的重量状态分为4种类型:

¨      标准型(Standard) 标记为S

¨      轻标型(Light or Standard) 标记为LS

¨      重标型(Heavy or Standard) 标记为HS

¨      轻重标准型(Light or Heavy or Standard) 标记为LHS

一个硬币为LHS状态，那是我们对它一无所知；LS和HS状态是有可能为轻的或有可能为重的，当然也可能是标准的；S状态是已知为标准的。

综上所述，问题的状态空间可表示成一个五元组:

(lhs，ls，hs，s，t )

其中前四个元素表示当前这四种类型硬币的个数，t表示所剩称硬币的次数。在这样的状态空间表示下，有:

初始状态：(12, 0, 0, 0, 3)

目标状态：sg₁：(0, 1, 0, 11, 0) 和 sg₂：(0, 0, 1, 11, 0)

sg₁、sg₂分别表示最后找到一个轻的或找到一个重的硬币，其余11个为标准硬币。

2．如何利用AO*算法求解

利用AO*算法求解问题需要找出如下要素:

(1)初始问题的描述。

(2)一组将问题变换成子问题的变换规则。

(3)一组本原问题描述。

    

该问题的初始问题前面已经表示出来了，本原问题就是两个目标状态。下面要定义一组转换规则。这里的转换规则就是每称一次，要考虑如何取硬币放到天平上，然后称完后，根据天平的状态，硬币的重量状态可能会从一种类型转变为另一种类型。

首先考虑如何取硬币的问题。设当前的状态为 (lhs，ls，hs，s，t)，用函数PICKUP([lhs₁, ls₁, hs₁, s₁],[ lhs₂, ls₂ , hs₂,s₂])表示本次分别从(lhs,ls , hs, s) 中取出了lhs₁,ls₁ , hs₁, s₁个硬币放到天平的左边，取出了lhs₂, ls₂ , hs₂, s₂个硬币放到天平的右边。对于PICKUP应默认有如下性质成立:

¨    0₁+ls₁+ hs₁ +s₁=lhs₂ +ls₂ +hs₂+s₂ ≤6，即天平两边的硬币数相等且小于等于6。

¨  lhs₁+lhs₂ ≤lhs∧ls₁+ls₂≤ls∧ hs₁+hs₂ ≤hs ∧ s₁+s₂≤s，即取出的硬币数小于等于相应类型原有的硬币数。

然后令PICKUP()等于-1,0,1 分别表示天平左倾斜、平衡和右倾斜。在这个定义下，有如下转换规则：

左倾斜规则：

if PICKUP([lhs₁, ls₁ ,hs₁, s₁],[ lhs₂, ls₂ , hs₂,s₂])= - 1∧ (lhs, ls , hs, s,t )

        then  (lhs′, ls′ , hs′, s′, t-1 )；

其中 s′= s+ ls-ls₂ + hs-hs₁+ lhs - (lhs₁+lhs₂) ；ls′=ls₂+lhs₂ ；hs′=lhs₁+hs₁；lhs′=0

这四个公式的含义分别是：若天平左倾,则在左天平的状态为LS的硬币，在右天平的状态为HS的硬币和未放到天平上的硬币都是标准的，即hs₂+ls₁+(lhs-lhs₁-lhs₂)+(ls-ls₁-ls₂)+(hs-hs₁-hs₂)个硬币的状态都改变为标准型；右天平原有的ls₂个轻标准型的硬币仍然为轻标准型，右天平的lhs₂个轻重标准型硬币改变为轻标准型；左天平原有的hs₁个重标准型的硬币仍然为重标准型，左天平的lhs₂个轻重标准型硬币改变为重标准型；只要不平衡，就不存在LHS型的硬币，天平上的硬币可以确定为LS或HS型，天平下的硬币可确定是S 型，这时lhs′=0。

平衡规则：

if PICKUP([lhs₁, ls₁ ,hs₁, s₁],[ lhs₂, ls₂ , hs₂,s₂])=0 ∧ (lhs, ls , hs, s,t )

        then  (lhs′, ls′ , hs′, s′, t-1 )；

其中 s′= s+ls₁+ls₂+hs₁+hs₂ +lhs₁+lhs₂；ls′=ls-ls₁-ls₂；hs′=hs-hs₁-hs₂；lhs′=lhs- lhs₁-lhs₂

这四个公式的含义分别是：若天平平衡，则所有在天平上的硬币都是标准的，即有ls₁+ls₂+ hs₁+hs₂ + lhs₁+lhs₂个硬币的状态都改变为标准型；左、右天平原有的轻标准型的硬币改变为标准型，所以从ls 中减去ls₁和ls₂；左、右天平原有的重标准型的硬币改变为标准型，所以也要从hs 中减去hs₁和hs₂；在平衡情况下，lsh型的硬币要减去左、右天平原有的轻重标准型的硬币，即lhs′= lhs-lhs₁-lhs₂。

右倾斜规则：

if PICKUP([lhs₁, ls₁ ,hs₁, s₁],[ lhs₂, ls₂ , hs₂,s₂])=1∧ (lhs, ls , hs, s,t )

        then  (lhs′, ls′ , hs′, s′, t-1 )；

其中 s′= s+ ls-ls₁ + hs-hs₂+ lhs - (lhs₁+lhs₂)；ls′=ls₁+lhs₁ ；hs′=lhs₂+hs₂；lhs′=0

这四个公式的与 L 规则的含义类似：若天平右倾，则在左天平上状态为 HS 的硬币和右天平上状态为 LS 的硬币以及未放到天平上的硬币都是标准的，即 hs ₁ +ls ₂ +(lhs-lhs ₁ -lhs ₂ )+(ls-ls ₁ -ls ₂ )+(hs-hs ₁ -hs ₂ ) 个硬币的状态都改变为标准型；左天平原有的 ls ₁ 个轻标准型的硬币仍然为轻标准型，左天平的 lhs ₁ 个轻重标准型硬币改变为轻标准型；右天平原有的重标准型的 hs ₂ 个硬币仍然为重标准型，右天平的 lhs ₂ 个轻重标准型硬币改变为重标准型；因为不平衡， lhs′=0 。 以上 3 个规则中 t-1 表示所剩使用天平的次数减少了一次。

3．如何在问题空间中搜索

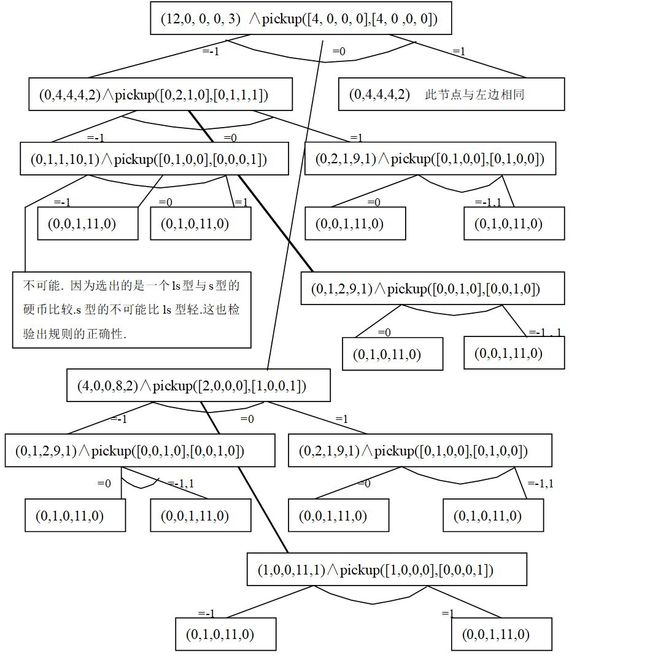
该问题可以用AO*算法求解，主要是基于这样的背景：用PICKUP()填入不同的参数表示一种选取方法，不同的选取方法之间是或的关系，当选定一组PICKUP的参数后，就必须考虑它的值为 -1、0、1时下层的节点都可解，则三种情况之间的关系为“与”的关系。这说明该问题的搜索图是与或图，图4-20给出了这样的搜索图的例子。

用于该算法的评价函数可设置为：

h((lhs，ls，hs，s，t))= ls+hs+lhs-1

显然有： h((0，1，0，11，0))=0 和h((0，0，1，11，0))=0 即h(sg₁)= h(sg₂)=0。

由于问题的本原问题对应得节点是可解节点，因此sg₁、sg₂为可解节点。不可解节点可定义为：如果节点n =(lhs，ls，hs，s，t )中t=0且(lhs，ls，hs，s)不属于{(0，1，0，11)，(0，0，1，11)} ，则n为不可解节点。

作好上述准备工作后，就可用AO*算法进行求解，下面图4-9就是用AO*算法得到得一个解图。

图4-9  利用AO*算法求解12硬币问题的解图

4. 求解过程的动画演示

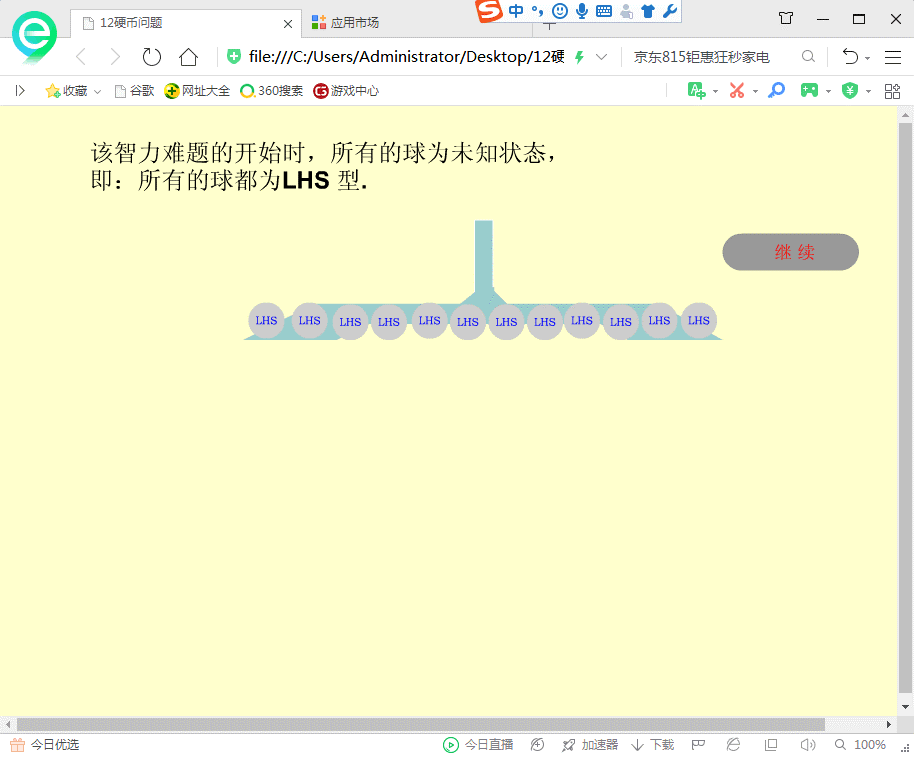
本演示交互式地展示12硬币问题的求解过程。从上面的求解方法分析可以看出，求解的关键是如何选取硬币到天平两端，什么状态的硬币、多少个？这一步由程序根据求解过程来提供。每次取完硬币到天平时，需要单击“继续”按钮。当出现下“left”、“balance”和“right”三个按钮时，表示要确定天平是否向左倾斜、平衡和右倾斜。此时由使用者确定，单击其中之一后，即可由程序确定(推理)出天平上和桌面上的硬币的状态。这是一个逻辑推理的过程，本游戏是来自于《趣味逻辑学》的给出的实例，确定硬币新的状态后，程序就可以进行各种状态的硬币数目的计算，然后进行下一步硬币的选取。

直接在浏览器中打开12ball.html，或直接双击12ball.html文件的图标，就可以看到图4.10所示的界面。

图4.10 初始状态为12个未知(轻、重、标准都可能)硬币在桌面

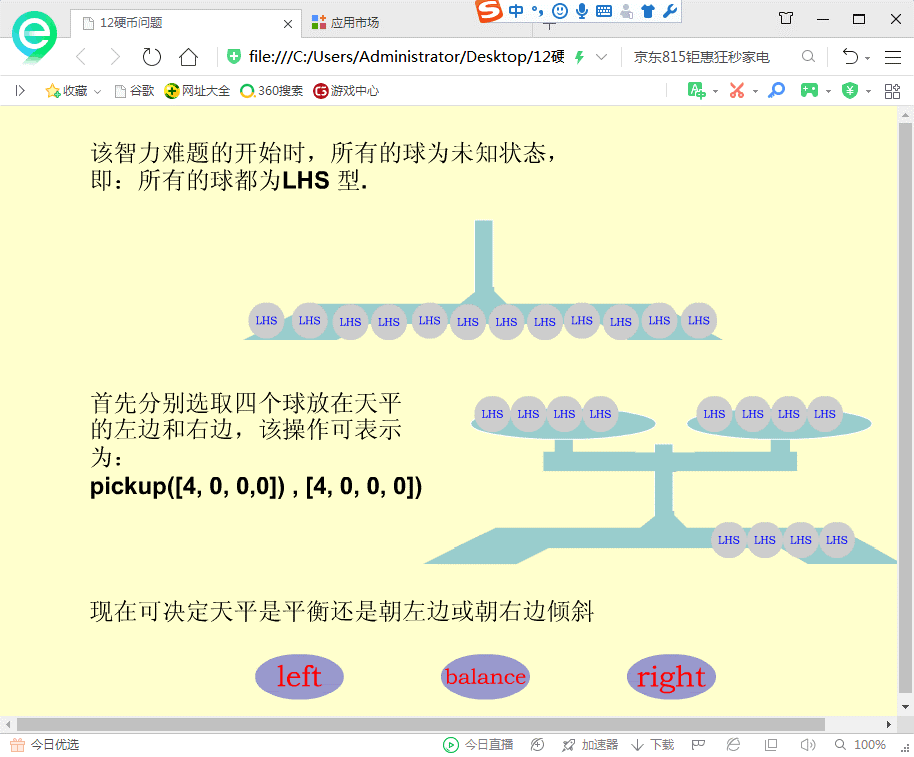
单击“继续”按钮，就可以看到图4.11所示的界面。

图4.11 程序自动选取各4个未知硬币到天平两边

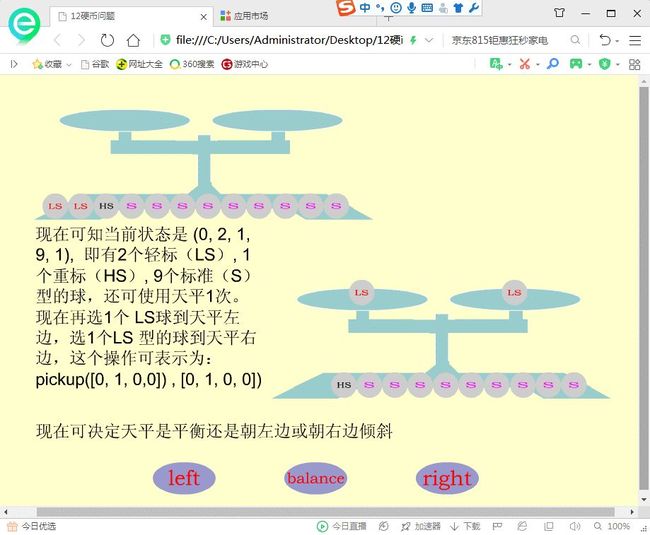
再单击“Left”按钮，天平左倾斜，天平和桌面上硬币随即发生变化，左边4个变成HS型，右边4个变成LS型，这8个硬币返回桌面，桌面的4个硬币也随即变为S型，现在就可以看到图4.12上部所示的界面。 再单击“继续”按钮，程序进行第二次硬币的选取，就可以看到图4.12中部所示的界面。

图4.12 天平左倾斜后再进行第二次硬币的选取后的界面

再单击“right”按钮，天平右倾斜，左边1个HS型变成S型，右边2个LS型变成S型，这6个硬币返回桌面，桌面的原来的2个HS型硬币、1个LS型硬币也随即变为S型，现在就可以看到图4.13上部所示的界面。 再单击“继续”按钮，程序进行第三次硬币的选取，就可以看到图4.13中部所示的界面。

图4.13 天平右倾斜后再进行第三次硬币的选取后的界面

此时，为什么要选择两个LS型的硬币到天平上，读者应该一目了然。现在还是有三种选择，再单击“balance”按钮，即天平平衡，左边1和右边的LS型变成S型，桌面的原来的1个HS型硬币，根据排除法也就可以定性了，现在就可以看到图4.14所示的界面。

图4.14 称完3次后的界面

这个演示程序可以展示不到27(<3³)种的12硬币问题的解，单击“重新开始”按钮，即可开始新的求解过程。

这个游戏的意义不仅让我们熟悉运用A^*求解问题，而且尝试用逻辑推理的方式思考问题和求解问题，并且尝试把取硬币、称天平这样的动作抽象成计算机操作的算子。

扫码，优惠购书

作者：朱福喜

定价：59元

ISBN：9787302458876

本书系统地阐述了人工智能的基本原理、实现技术及其应用，全面地反映了国内外人工智能研究领域的最新进展和发展方向。全书共19章，分为4个部分：第1部分是搜索与问题求解，用8章的篇幅系统地叙述了人工智能中各种搜索方法求解的原理和方法，内容包括状态空间和传统的图搜索算法、和声算法、禁忌搜索算法、遗传算法、免疫算法、粒子群算法、蚁群算法和Agent技术等；第2部分为知识与推理，用4章的篇幅讨论各种知识表示和处理技术、各种典型的推理技术，还包括非经典逻辑推理技术和非协调逻辑推理技术；第3部分为学习与发现，用3章的篇幅讨论传统的机器学习算法、神经网络学习算法、数据挖掘和知识发现技术；第4部分为领域应用，用3章分别讨论专家系统开发技术和自然语言处理原理和方法。

扫码，优惠购书

作者：朱福喜 朱丽达

定价：69.80元

ISBN：9787302519669

本书作为作者已出版多次的《人工智能》教材的配套教辅材料，其章节与原教材基本对应，但内容分为学习目标与要求、知识要点、原教材对应的习题解析、补充题、课堂演示与实验指导5个部分。其中，学习目标与要求为每章要达到的学习目标；知识点与原教材的内容对应，基本上全面介绍了人工智能的理论与技术；习题解析对每章的习题进行了解答；补充题对原教材的习题进行了补充，并给出了解答。