统计学习方法——第三章K近邻

【K近邻算法】

       一个少数服从多数的投票模型，可以用在多分类的情况。

算法描述：

       KNN是根据点与点之间的关系来进行判断，所以有些噪声可能会对结果有些影响。还有KNN并不需要训练，但需要遍历整个训练集，所以预测会比较慢。

【代码中用到的方法】

np.linalg.norm(a-b)     #欧氏距离

np.dot(a,b)                #按照矩阵乘法规则来运算

【算法举例】

 【代码】

链接：
http://blog.csdn.net/wds2006sdo/article/details/51933044
http://blog.csdn.net/haluoluo211/article/details/78177510

-----------------------------------------------------------------------------------------------------------------------------------------------

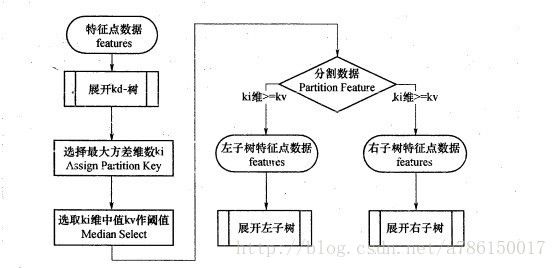
【KD-树】

       更详细参见文章

http://blog.csdn.net/yan456jie/article/details/52074141

http://www.cnblogs.com/v-July-v/archive/2012/11/20/3125419.html

       是对数据点在k维空间（如二维(x，y)，三维(x，y，z)，k维(x1，y，z..)）中划分的一种数据结构，主要应用于多维空间关键数据的搜索（如：范围搜索和最近邻搜索）。就是把整个空间划分为特定的几个部分，然后在特定空间的部分内进行相关搜索操作。

【算法举例】

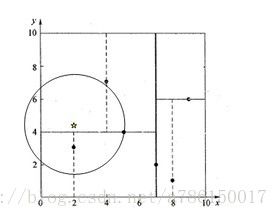
       6个二维数据点{(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)}构建kd树的具体步骤为：

• 确定：split域=x。具体是：6个数据点在x，y维度上的数据方差分别为39，28.63，所以在x轴上方差更大，故split域值为x；
• 确定：Node-data = （7,2）。具体是：根据x维上的值将数据排序，6个数据的中值(所谓中值，即中间大小的值)为7，所以Node-data域位数据点（7,2）。这样，该节点的分割超平面就是通过（7,2）并垂直于：split=x轴的直线x=7；
• 确定：左子空间和右子空间。具体是：分割超平面x=7将整个空间分为两部分：x<=7的部分为左子空间，包含3个节点={(2,3),(5,4),(4,7)}；另一部分为右子空间，包含2个节点={(9,6)，(8,1)}；

【基本算法】

A. k-d树的数据结构      # class KD_node

代码：

class KD_node:
    def __init__(self,elt=None,split=None,LL=None,RR=None):
        """
        elt:样本点，即根节点
        split:划分域
        LL,RR:左右子空间内数据点构成的kd-tree
        """
        self.elt = elt
        self.split = split
        self.left = LL
        self.right = RR

B.划分维度的原理   # computeVariance(arr)

       （基于方差的选择方法）尽可能将相似的点放在一颗子树里面，所以kd-tree采取的思想就是计算所有数据点在每个维度上的数值的方差，然后方差最大的维度就作为当前节点的划分维度。

代码：

def computeVariance(arr):
    """
    var = E[X^2] - (E(X))^2
    """
    sum1 = sum(arr)
    mean = sum1/arr.size
    arr2 = arr * arr  #list不能相乘
    sum2 = sum(arr2)
    
    return sum2/arr.size - mean ** 2

C.k-d树的创建  # createKDTree(root,data_list)

代码：

def createKDTree(root,data_list):
    """
    root:当前树的根节点  
    data_list:数据点的集合(无序)  
    return:构造的KDTree的树根
    
    LEN:数据点的个数
    demension:数据点的维数
    """
    if len(data_list) == 0:
        return
    
    LEN = len(data_list)
    demension = len(data_list[0])
    
    var_max = 0
    split = 0
    for d in range(demension):
        arr1 = np.array(demension)[:,d]
        var = computeVariance(arr1)
        
        #找出方差最大的那一维,记为split
        if var_max < var:
            var_max = var
            split = d
        
    #根据选择的划分域对数据点进行排序,方便分配左右儿子
    data_list = sorted(data_list,key = lambda x:x[split])
    elt = data_list[LEN//2]
    
    root = KD_node(elt,split)
    root.left = createKDTree(root.left,data_list[:LEN//2])
    root.right = createKDTree(root.right,data_list[LEN//2+1:])
    
    return root

D.利用kd-tree进行最近邻的查找#findNN(root,query)

1.二叉查找：

       从根节点开始进行查找，直到叶子节点；在这个过程中，记录最短的距离，和对应的数据点；同时维护一个栈，用来存储经过的节点

2.回溯查找：

       通过计算查找点到分割平面的距离(这个距离比较的是分割维度上的值的差，并不是分割节点到分割平面上的距离，虽然两者的值是相等的)与当前最短距离进行比较，决定是否需要进入节点的相邻子空间进行查找

e.g

已知：

• 图中的黑点为kd-tree中的数据点，五角星为查询点；
• 通过kd-tree的分支决策会将它分到坐上角的那部分空间，但并不是意味着它到那个空间中的点的距离最近

步骤：

1）首先扫描到叶子节点，扫描过程中记录的最近点为p（5，4），最短距离为d；

2）现在开始回溯，假设分割的维度为ss，其实回溯的过程就是确定是否有必要进入相邻子空间进行搜索，确定的依据就是当前点到最近点的距离d是否大于当前点到分割面（在二维空间中实际上就是一条线）的距离L，如果d < L,那么说明完全没有必要进入到另一个子空间进行搜索，直接继续向上一层回溯；如果有d > L,那么说明相邻子空间中可能有距查询点更近的点。

代码：

def findNN(root,query):
    """
    root:KDTree的树根 
    query:查询点 
    return:返回距离data最近的点NN，同时返回最短距离min_dist 
    
    nodeList:用来存储二分查找经过的节点，先进后出，方便回溯查找
    back_elt:回溯查找找弹出的节点
    ss:分割的维度
    """
    NN = root.elt
    min_dist = np.linalg.norm(np.array(NN)-np.array(query))
    
    nodeList = []
    temp_root = root
    #二叉查找,直到叶子节点
    while temp_root:
        nodeList.append(temp_root)
        dist = np.linalg.norm(np.array(temp_root.elt)-np.array(query))
        
        if dist < min_dist:
            NN = temp_root.elt
            min_dist = dist
            
        #当前节点的划分域  
        ss = temp_root.split
        if query[ss] < temp_root[ss]:
            temp_root = temp_root.left
        else:
            temp_root = temp_root.right
    
    #回溯查找,将nodeList遍历一遍
    while nodeList:
        back_root = nodeList.pop()
        back_elt = back_root.elt
        ss = back_root.split
        
        """
        if min大于query到分割面的距离:
            相邻子空间可能存在更近的点
        """
        if abs(query[ss] - back_elt[ss]) < min_dist: 
            if query[ss] > back_elt[ss]:
                temp_root = back_root.left
            else:
                temp_root = back_root.right
            #类似二分查找
            if temp_root:
                nodeList.append(temp_root)
        
                #相邻子空间找更近的点
                dist = np.linalg.norm(np.array(temp_root.elt)-np.array(query))
            
                if dist < min_dist:
                    NN = temp_root.elt
                    min_dist = dist
    return NN,min_dist