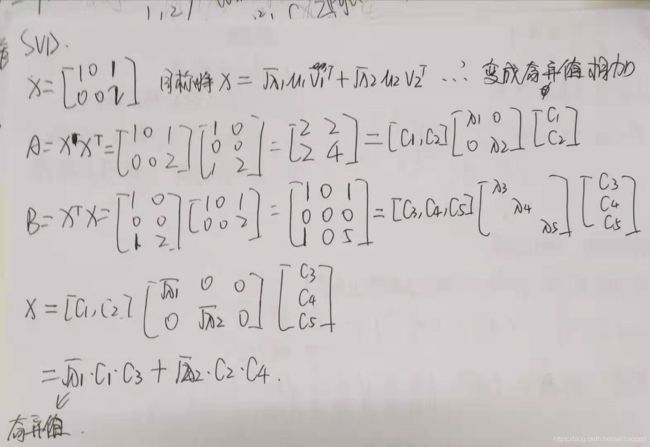机器学习笔试面试题——day2
选择题
1、以下不属于影响聚类算法结果的主要因素有()
A 已知类别的样本质量
B 分类准则
C 特征选取
D 模式相似性测度
聚类不知道类别
2、模式识别中,不属于马式距离较之于欧式距离的优点的是( )
A 平移不变性
B 尺度不变性
C 考虑了模式的分布
缺点
1)马氏距离的计算是建立在总体样本的基础上的,即同样的样本在不同的总体中距离是不一样的
2)要求协方差逆矩阵必须存在(总体样本数大于样本维度且样本不共线),否则用欧式距离;由于协方差矩阵的存在,导致马氏距离不稳定
3)它夸大了变化微小的变量的作用
优点
1)尺度不变性,不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关;
2)由标准化数据和中心化数据(即原始数据与均值之差)计算出的二点之间的马氏距离相同。
3)考虑了变量的相关性
马氏和欧式距离都具有:平移不变性和旋转不变性
标准差![]() 方差;协方差
方差;协方差![]()
3、影响基本K-均值算法的主要因素有()
A 样本输入顺序
B 模式相似性测度
C 聚类准则
4、在统计模式分类问题中,当先验概率未知时,可以使用()
A 最小损失准则
B 最小最大损失准则
C 最小误判概率准则
先验概率未知时,采用最小最大误判准则,N-P准则
5、如果以特征向量的相关系数作为模式相似性测度,则影响聚类算法结果的主要因素有( )
A 已知类别样本质量
B 分类准则
C 量纲
以特征向量的相关系数作为模式相似性度量
那么分类准则和特征选取会影响聚类算法6、以下属于欧式距离特性的有()
A 旋转不变性
B 尺度缩放不变性
C 不受量纲影响的特性
7、以下( )不属于线性分类器最佳准则?
A 感知准则函数
B 贝叶斯分类
C 支持向量机
D Fisher准则
线性分类器三大准则:
感知器准则函数:使错分类样本到分类界面距离之和最小,通过错分类样本信息对分类器函数修正
SVM:分类界面使两类间隔最大,期望泛化风险最小
Fisher准则:LDA线性判别分析,样本投影到一条直线上,类内距离小,类间距离大,最大化广义瑞利熵
8、一监狱人脸识别准入系统用来识别待进入人员的身份,此系统一共包括识别4种不同的人员:狱警,小偷,送餐员,其他。下面哪种学习方法最适合此种应用需求:
A 二分类问题
B 多分类问题
C 层次聚类问题
D k-中心点聚类问题
E 回归问题
F 结构分析问题
9、关于 logit 回归和 SVM 不正确的是()
A Logit回归目标函数是最小化后验概率
B Logit回归可以用于预测事件发生概率的大小
C SVM目标是结构风险最小化
D SVM可以有效避免模型过拟合
10、有两个样本点,第一个点为正样本,它的特征向量是(0,-1);第二个点为负样本,它的特征向量是(2,3),从这两个样本点组成的训练集构建一个线性SVM分类器的分类面方程是( )
A 2x+y=4
B x+2y=5
C x+2y=3
D 2x-y=0
11、下列时间序列模型中,哪一个模型可以较好地拟合波动性的分析和预测。
A AR模型
B MA模型
C ARMA模型
D GARCH模型
AR模型:
该模型认为通过时间序列过去时点的线性组合加上白噪声即可预测当前时点,AR模型在金融模型中主要是对金融序列过去的表现进行建模,如交易中的动量与均值回归。
MA模型:
和AR大同小异,它不是是历史时序值的线性组合而是历史白噪声的线性组合。与AR最大的不同之处在于,AR模型中历史白噪声的影响是间接影响当前预测值的(通过影响历史时序值)。在金融模型中,MA常用来刻画冲击效应,例如预期之外的事件。
ARAM模型:
将AR和MA模型混合可得到ARMA模型
ARIMA模型是在ARMA模型的基础上解决非平稳序列的模型,因此在模型中会对原序列进行差分
在ARIMA模型的基础上可以衍生出SARIMA模型,SRIMA模型能够刻画季节效应,如商品价格的周期性变动
GARCH模型:
对误差的方差进行了进一步的建模。特别适用于波动性的分析和预测,这样的分析对投资者的决策能起到非常重要的指导性作用,其意义很多时候超过了对数值本身的分析和预测。
12、以下说法中错误的是()
A SVM对噪声(如来自其他分部的噪声样本)具备鲁棒性
B 在adaboost算法中,所有被分错样本的权重更新比例不相同
C boosting和bagging都是组合多个分类器投票的方法,二者都是根据单个分类器的正确率确定其权重
D 给定n个数据点,如果其中一半用于训练,一半用户测试,则训练误差和测试误差之间的差别会随着n的增加而减少的
具体说来,整个Adaboost 迭代算法就3步:
1)初始化训练数据的权值分布。如果有N个样本,则每一个训练样本最开始时都被赋予相同的权值:1/N。
2)训练弱分类器。如果样本被正确分类,在下一个训练集中权重被降低,反之,则提高。更新过的样本集被用于训练下一个分类器。
3)将各个训练得到的弱分类器组合成强分类器。增加分类误差率小的弱分类器权重,降低误差大的,| boosting | bagging | |
| 结果 | Adaboost通过加权多数表决;提升树通过拟合残差 | 投票得到分类结果;回归问题计算均值 |
| 样本选择 | 每一轮训练集不变,变的是样例的权重 | 从原始样本中抽取训练集,有放回的,k个训练集之间相互独立 |
| 样例权重 | 根据错误率不断调整,错误率大的权重大 | 均匀抽样 |
| 预测函数 | 权重根据错误率变化,误差小的分类器权重大 | 所有预测函数权重相等 |
| 并行计算 | 必须顺序进行 | 可以并行 |
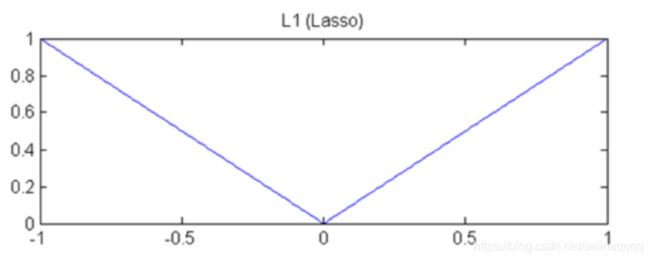
13、你正在使用带有 L1 正则化的 logistic 回归做二分类,其中 C 是正则化参数,w1 和 w2 是 x1 和 x2 的系数。当你把 C 值从 0 增加至非常大的值时,下面哪个选项是正确的?
A 第一个 w2 成了 0,接着 w1 也成了 0
B 第一个 w1 成了 0,接着 w2 也成了 0
C w1 和 w2 同时成了 0
D 即使在 C 成为大值之后,w1 和 w2 都不能成 0
L1正则化的函数如图所示,w1,w2可以为0,但是是对称的,不会出现一个为0一个不为0的情况
14、在 k-均值算法中,以下哪个选项可用于获得全局最小?
A 尝试为不同的质心(centroid)初始化运行算法
B 整迭代的次数
C 找到集群的最佳数量
D 以上所有
15、假设你使用 log-loss 函数作为评估标准。下面这些选项,哪些是对作为评估标准的 log-loss 的正确解释。
A 如果一个分类器对不正确的分类很自信,log-loss 会严重的批评它
B 对一个特别的观察而言,分类器为正确的类别分配非常小的概率,然后对 log-loss 的相应分布会非常大
C log-loss 越低,模型越好
D 以上都是
16、下面哪个选项中哪一项属于确定性算法?
A PCA
B K-Means
C 以上都不是
确定性算法表示再运行一次,结果一样,PCA是,而K-means不是
17、两个变量的 Pearson 相关性系数为零,但这两个变量的值同样可以相关。这句描述是正确还是错误?
A 正确
B 错误
皮尔逊系数只能衡量线性关系,不能衡量非线性关系18、下面哪个/些超参数的增加可能会造成随机森林数据过拟合?
A 树的数量
B 树的深度
C 学习速率
19、下列哪个不属于常用的文本分类的特征选择算法?
A 卡方检验值
B 互信息
C 信息增益
D 主成分分析
文本分类常采用特征选择方法。
1)DF文档频率
统计特征词出现的文档数量
2)MI互信息法
用于衡量特征词与文档类别直接的信息量。
如果某个特征词的频率很低,那么互信息得分就会很大,因此互信息法倾向"低频"的特征词。
相对的词频很高的词,得分就会变低,如果这词携带了很高的信息量,互信息法就会变得低效。
3)信息增益法
通过某个特征词的缺失与存在的两种情况下,语料中前后信息的增加,衡量某个特征词的重要性。
4)卡方检验法
利用了统计学中的"假设检验"的基本思想:首先假设特征词与类别直接是不相关的
如果利用CHI分布计算出的检验值偏离阈值越大,那么更有信心否定原假设,接受原假设的备则假设:特征词
与类别有着很高的关联度。
5)WLLR(Weighted Log Likelihood Ration)加权对数似然
6)WFO(Weighted Frequency and Odds)加权频率和可能性
20、机器学习中做特征选择时,可能用到的方法有?
A 卡方
B 信息增益
C 平均互信息
D 期望交叉熵
E 以上都有
手撕代码
1 归并排序
public class merge{
public static int sort(int[] A, int start, int end){
if(start2 快排序(递归和非递归)
public class QuickSort{
//返回基准的下标index
public int partition(int[] a,int left,int right){
int left = i;
int right =j;
int key = a[left];
if(ikey)
j--;
while(a[i]left+1){
stack[top++] = left;
stack[top++] = index-1;
}
if(index0){
right = stack[--top];
left = stack[--top];
index = partition(a,left,high);
if(index>left+1){
stack[top++] = left;
stack[top++] = index-1;
}
if(index 3 二叉树后序遍历
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
public class Order{
//以数组的形式建立一个二叉树
public static void main(String[] args){
for(int i=0;i<10;i++){
node[i] = new TreeNode(i);
}
for(int i=0;i<10;i++){
if(i*2+1<10)
node[i].left = node[i*2+1];
if(i*2+2<10)
node[i].right = node[i*2+2];
}
preOrder(node[0]);
}
//前序递归
public static void preOrder(TreeNode biTree){
System.out.println(biTree.val);
TreeNode leftTree = biTree.left;
if(leftTree!=null){
preOrder(leftTree);
}
TreeNode rightTree = biTree.right;
if(rightTree!=null){
preOrder(rightTree);
}
}
//后序递归
public static void postOrder(TreeNode biTree){
TreeNode leftTree = biTree.left;
if(leftTree!=null){
postOrder(leftTree);
}
TreeNode rightTree = biTree.right;
if(rightTree!=null){
postOrder(rightTree);
}
System.out.println(biTree.val);
}
}4 给前序和中序,求出这个二叉树
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
public class tree{
public static TreeNode rebuildTree(int [] preOrders,int [] inOrders){
if(preOrders.length == 0||inOrders.length==0){
return null;
}
return buildTree(preOrders, 0, preOrders.length-1, inOrders, 0, inOrders.length-1);
}
public static TreeNode buildTree(int[] preOrders, int preStart, int preEnd, int[] inOrders, int inStart, int inEnd){
//前序第一个为根节点
int root = preOrders[preStart];
TreeNode tn = new TreeNode(root);
tn.left = null;
tn.right = null;
//去中序里找到这个节点
int index = -1;
for(int i =0;i0){
tn.left = buildTree(preOrders,left_preStart,left_preEnd,inOrders,left_inStart,left_inEnd);
}
if(left_length 机器学习算法
1 LR和Hinge损失函数手推以及其他损失函数总结
| 常用损失函数 | 公式 | 应用 |
| 平方损失 | 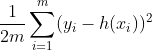 |
线性回归 |
| 交叉熵损失(LogLoss) | 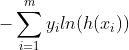 |
逻辑回归,softmax,sigmod |
| Hinge损失 | 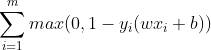 |
SVM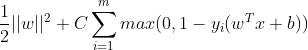 |
| 指数损失 | 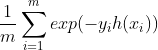 |
Adaboost |
| 0-1损失 |
2 PCA和SVD
对中心化后样本矩阵做SVD的过程就是PCA
3 聚类算法原理以及优缺点
| K-Means | DBSCAN | |
| 输入 | 初始质心k | 最少点数k,半径Eps |
| 重复 | 对每个样本计算到其最近的质心并标类别,重新计算质心 | 判断输入点是否为核心对象,找到核心对象的所有密度可达点 |
| 结束条件 | 质心不再变化 | 所有点输入完毕 |
| 非球形数据 | 很难处理,对于不同大小的簇也很难处理 | 可以处理 |
| 稀疏高维数据 | 可以用于稀疏高维数据 | 性能很差 |
| 重叠的簇 | 可以发现重叠的簇 | 直接合并这些簇 |
| 簇的选取 | 过于依赖初始质心的k的选取,k的选取可以有枚举法和C-H准则(类间方差大,类内方差小) | 可以自动选取簇 |
| 时间复杂度 | O(m) | O(m^2) |