计算机网络中出现异常流量,计算机网络下网络流量异常的检测算法

杨军

摘要： 文章首先简要阐述了网络流量异常检测的重要意义，在此基础上对计算机网络环境下网络流量异常的检测算法进行论述。期望通过本文的研究能够对网络运行稳定性的提升有所帮助。

【关键词】计算机网络 网络流量 异常检测算法

1 网络流量异常检测的重要意义

对于计算机网络而言，网络流量是对整个网络运行状态进行研究的重要前提和基础，在网络当中，物理层的数据单位是比特，而数据链路层的单位是帧，由于数据单位本身的特殊性，使得无法对网络异常进行直观分析。同时，网络层是以数据包作为单位，在它的流量特性分析的基础上，可对网络应用及行为进行检测。在网络结构中，可将网络流量数据用图1表示。

大体上可将网络数据异常检测的意义归纳为以下几个方面：

1.1 反映网络性能

对网络流量进行检测是性能评估的关键部分，主要包括网络中的关键设备、网络链路以及服务器等方面的性能评估，由此可获得相关业务的带宽占用情况，为设备性能瓶颈的确定提供依据。当网络流量超出网络的实际承载能力时，会使网络的性能随之下降，从而无法高效完成数据的传输与处理，为使网络的性能得到进一步改善，可通过检测流量特性，并从其中对相关的参数进行提取，借此来找出影响网络性能的因素，对网络流量进行控制，保证网络性能始终处于最优状态。

1.2 为网络故障诊断提供依据

在计算机网络环境中，如果数据流量正常，则表明网络的运行稳定，而当网络出现故障时，流量的特征数据会出现异常，基于这一前提，使得数据流量成为判断网络异常及故障检测的重要依据。网络中某个设备出现故障或是配置错误，均会使网络性能受到一定程度的影响，严重时可能会对整个网络造成致命的破坏，运维管理人员通过对网络流量数据的检测分析，可以及时发现问题的根源之所在，为故障解决与处理提供可靠的依据。同时网络流量异常检测算法，能够提供流量特征，并对这些特征进行组合，还能对不同的网络攻击进行检测。

1.3 全面分析应用

现如今，在计算机网络技术快速发展的推动下，网络的规模进一步扩大，其中承载的业务也随之具有了复杂性和多样性的特点，与此同时，各种网络应用大量出现并随着网络发展不断更新和升级。网络带宽瓶颈、峰值流量以及预测流量变化趋势，是网络应用设计与运维人员所面临的主要问题。对网络流量进行检测分析，能够使上述问题得到解决，并对网络应用层的变化情况进行确定，由此可准确掌握应用的相关指标。

1.4 为网络协议的优化改进提供依据

在网络分层结构体系当中，各层之间的数据传输，需要借助相关的通信协议来实现，网络协议会随着业务需求不断更新，它的标准则是数据传输的保障。现如今，随着带宽的逐步增加和应用层中新业务的大量出现，对网络通信协议设计提出越来越高的要求，通过网络流量进行检测分析，可将检测到的数据作为模型设计的输入参数，由此可为网络协议的优化提供依据。

2 计算机网络环境下网络流量异常的检测算法

2.1 网络异常流量分析

对网络异常进行检测的基本标准是通过对实际流量与正常流量的比较，看是否存在偏差，如果有，则对异常的流量数据进行确定，由于这种数据具有相应的属性特征，所以可将具体的特征作为异常的判断依据。在计算机网络环境中，最难检测的异常情况为恶意攻击所产生的流量异常，通过对异常的分析，选择适宜的数据属性特征便可进行检测。DDOS是计算机网络中最为常见的一种攻击，它以DOS为基础，原本的DOS攻击是一对一的方式，而DDOS则是分布式的攻击，通过对被控制计算机的远程操控，可使海量攻擊数据入侵目标主机，进而使主机的系统崩溃，并使网络瞬时拥塞，由此将会导致网络瘫痪。

2.1.1 DDOS攻击

在DDOS攻击发生时，会随之出现一些共同的特征，具体如下：网络总会有大量指向被攻击主机的数据包；无用数据包在网络中的大量分布会造成网络拥塞；如果攻击者采用的是伪造IP技术进行攻击，则会在短时间内，使网络中出现虚假的源IP地址，而以真实IP发动攻击，会使网络中出现分散的IP地址。通常情况下，DDOS只针对目标主机进行集中攻击，由此使得流量数据中IP数量相对较少，并且比较集中，被攻击的网络因伪造IP技术的运用，使得流量数据呈现出分布、分散、数量大等特征。

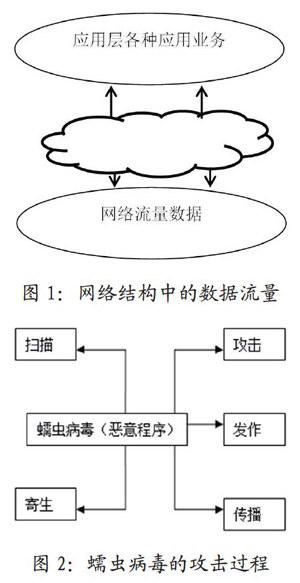
2.1.2 蠕虫病毒

此类病毒与常规的计算机病毒有着非常明显的差别，这种差别具体体现在对网络的攻击过程上，具体如图2所示。

这种病毒可自行运行，通过软件系统中存在的缺陷和漏洞，获取对相应系统的控制权，并在计算机网络中进行传播，由于该病毒本身具有很强的繁殖性，从而使网络及系统资源产生巨大的消耗。由蠕虫病毒的攻击流程可知，它是从一个IP向网络中多个IP的某个端口发起连接请求，随即对蠕虫病毒进行迅速传播，从而引起网络瞬时拥塞，严重时会造成网络瘫痪。一旦蠕虫病毒发生，源主机会对数量更多的目标机进行感染，在这一过程中，会产生出数量较多的数据包，它们之间的源IP地址相同，但目的IP却较为分散。如果计算机网络中出现蠕虫病毒，那么流量数据会表现出如下特征源IP地址少但较为集中，目的IP地址多，但较为分散。

2.2 TCM-KNN算法

直推信度机简称TCM，这是一种具体较强适应性的机器学习机制，它以随机性的思想理论为依托，能够对多个类别的可信程度进行衡量。但由于随机性无法进行准确计算，所以需要建立一个能够计算，并且还符合随机性原理的检测函数，对置信度进行评估。KNN是一种较为典型的分类算法，也被称之为K-邻近算法，它在对分类进行建立的过程中，无需假定分布结构，因该算法的计算过程较为简单，加之易于实现，从而使其周期网络异常流量检测中得到广泛应用。但在实际应用中发现，如果样本处于不平衡的条件时，则可能会使待分类的样本被分到不是目标类的大样本当中，由此会对检测结果的准确性造成影响。本文所提出的TCM-KNN算法是上述两种算法的融合，可也将其称之为结合算法。下而重点对该算法在网络流量异常检测中的应用进行分析。

在应用TCM-KNN算法对网络流量异常进行检测的过程中，需要构建起一个正常的行为模型，据此对待检测的流量数据进行判定，看是否正常。对于正常类别y而言，待检测流量数据样本i的对应奇异值αiy可用下式表示：

通过式(1)的计算方法进行计算后，异常流量样本的奇异值要大于正常样本奇异值，这样便于区分正常与异常流量数据。在TCM-KNN算法中，需要对待测样本与簇的中心距进行计算，选取距离最短的簇作为正常训练集。通常情况下，距离越短，表明待测样本与簇内样本的相似程度越高，经过计算，可以得到待测及正常样本的奇异值，若是P值比预先设定好的闽值小，说明置信度较高，可用1-τ作为异常流量数据判定的关键性指标。

2.3 算法实验

为对本文所提出的TCM-KNN算法的可行性及有效性等方而进行验证，先对网络中的正常数据进行聚类，同时为使实验过程变得更加简单和方便，选取DARPA数据集进行试验验证。具体的实验方法如下：选取第一周的正常数据作为正常数据的训练集，同时选取第二周的数据作为待检测数据，第二周的数据集当中，存在多种不同类型的攻击实例，因此，可用于对TCM-KNN算法的验证。检测率与误报率是目前国际上通用的两个评价指标。实验步骤如下：

采用随机抽取的方式，从第一周的数据中对正常数据进行选取，然后从第二周的数据中，对待测数据进行选取，再从第三周数据中，选取正常数据来完成异常流量检测。在对TCM-KNN算法进行应用的过程中，需要对置信度闽值进行设定，结合前人的研究成果，该值设定为0.05。在对本文提出的TCM-KNN算法进行验证的过程中，为更加直观地反映出该算法在网络流量异常检测方而的准确程度，本次实验通过数据对比的方法进行具体验证(限于篇幅，数据选取及计算过程省略)。在算法的验证中，k值的选取是关键性环节，既不可过小，也不宜过大，以免对算法的准确性造成影响。需要注意的是，随着k值的增大，检测时问会随之延长，因此，在对该算法进行实际应用时，要对以下因素进行综合考虑：准确率、有效性以及耗时等。经过验证，建议在应用TCM-KNN算法对网络流量异常进行检测时，k值可以选择8，由此能够获得理想的检测结果。由此可见，本文所提出的TCM-KNN算法在网络流量异常检测中具有良好的适用性，只要k值选择的合理，便可以确保检测结果的准确率。

3 结论

综上所述，在计算机网络环境当中，为确保网络运行的稳定性，就必须保证网络流量始终处于正常状态，然而受到DDOS及蠕虫病毒的攻击，会造成网络流量异常，对此，本文提出一中检测算法，即TCM-KNN算法，经过该算法在网络流量异常检测中具有良好的适用性，当k值选择合理时，能确保检测结果的准确率。

参考文献

[1]吕军晖，于龙洋，张瑾.Ntada： -种网络流量异常检测算法[J].经济与管理战略研究，2012( 01)：128-146

[2]朱俚治，朱梧 木檀.一种检测网络流量异常和网络攻击的算法[J].计算技术与自动化，2017，36 (01)：92-97.

[3]叶坤，网络流量异常检测方法的研究与改进[J].南京工业大学，201 5.

[4]朱俚治，粗糙集与MMTD算法的网络流量异常研究[J].计算机与数字工程，2 17( 01)：110-114.

[5]吕军，李星，一种网络流量异常检测算法[J].计算机应用研究，2006，23(11)：217-219.

[6]米捷，王佳欣，多层次数据中心网络流量异常检测算法[J].河南工程学院学报(自然科学版)，2 01 7，29 (01)： 62-66.

[7]曾建华.一种基于核PCA的网络流量异常检测算法[J].计算机应用与软件，2018 (03)：140-144.

[8]付强，甘亮，李爱平，吴泉源.一种基于主成分分析算法的网络异常检测实现[J].南京师范大学学报(工程技术版).2008，8 (04)：13-16，

[9]侯重遠，江汉红，芮万智，刘亮.工业网络流量异常检测的概率主成分分析法[J]，西安交通大学学报，2012，46 (02)： 70-75.