基于循环卷积的一维小波变换程序验证（C语言）

---

前言

最近对循环卷积、小波变换比较感兴趣，阅读了一些文章，也有了一些收获。在学习的过程中，无意间看到了一篇名为《一维小波变换，可多次分解》的博客-https://blog.csdn.net/lichengyu/article/details/5829785。该博客分享了代码，并进行了小波变换多次分解分析，但遗憾的是，没有介绍实现平台、博客图片看不到，且有读者反映代码实现有一定问题，影响学习和体验。

出于上述原因，本文基于原代码进行适当修改并在Visual C++ 6.0上编译实现；为验证代码效果，将运算结果与MATLAB中dwt函数获得的结果进行比较分析；结果显示，所写代码能较好实现对原始信号的分解。

---

一、工具介绍及下载（Visual C++ 6.0/MATLAB）

1. Visual C++ 6.0

Visual C++是Microsoft公司推出的功能最强大、也是最复杂的程序设计工具之一。它最常用的版本为Visual C++ 6.0。
Visual C++ 6.0集程序的代码编辑、编译、连接、调试等功能于一体，为编程人员提供了一个既完整又方便的开发环境。

[下载链接]：
https://pan.baidu.com/s/1qDKJQHXf29XqxBe8hfhQaQ
[提取码]: 6bxk

2. MATLAB

MATLAB是美国 MathWorks 公司出品的商业数学软件 ，用于数据分析 、无线通信 、深度学习 、图像处理与计算机视觉 、信号处理 、量化金融与风险管理、机器人， 控制系统等领域。MATLAB是matrix&laboratory两个词的组合，意为矩阵工厂（矩阵实验室），软件主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。

[下载链接]：
https://pan.baidu.com/s/1jnp9OeXZRnwScGU68K03CQ
[提取码]: 1234

---

二、一维小波变换C语言代码

1. 基于循环卷积的一维小波变换程序（Visual C++ 6.0）

代码如下：

#include 
#include 
#include 

#define  LENGTH  4320  // 信号长度,本例中原始信号为4320个数据点(matlab中leleccum信号)
/*****************************************************************
*　函数: 一维卷积函数
*
*　说明: 循环卷积,卷积结果的长度与输入信号的长度相同
*
*　输入参数: data[],  输入信号;
*            h[],     Daubechies 3 小波基低通滤波器系数;
*　			 g[],     Daubechies 3 小波基高通滤波器系数;
*            cov[],   卷积结果;
*			 n,       输入信号长度; 
*            m,       卷积核长度.
*****************************************************************/
void Covlution(double data[], double h[], double g[], double cov[], int n, int m)
{
	int i = 0;
	int j = 0;
	int k = 0;

	// 将cov[]清零
	for(i = 0; i < n; i++)
	{
		cov[i] = 0;
	}

	// ****************************************************
	// 奇数行用h[]进行卷积
	// ****************************************************

	// 前m/2+1行
	i = 0;
	for(j = 0; j < m/2; j+=2, i+=2)
	{
		for(k = m/2-j; k < m; k++ )
		{
			cov[i] += data[k-(m/2-j)] * h[k];   // k针对core[k]
		}

		for(k = n-m/2+j; k < n; k++ )
		{
			cov[i] += data[k] * h[k-(n-m/2+j)]; // k针对data[k]
		}
	}

	// 中间的n-m行
	for( ; i <= (n-m)+m/2; i+=2)
	{
		for( j = 0; j < m; j++)
		{
			cov[i] += data[i-m/2+j] * h[j];
		}
	}

	// 最后m/2-1行
	// i = ( (n - m) + m/2 + 1 )/2*2;
	for(j = 1; j <= m/2; j+=2, i+=2)
	{
		for(k = 0; k < j; k++)
		{
			cov[i] += data[k] * h[m-j-k];     // k针对data[k]
		}

		for(k = 0; k < m-j; k++)
		{
			cov[i] += h[k] * data[n-(m-j)+k]; // k针对core[k]
		}
	}

	// ****************************************************
	// 偶数行用g[]进行卷积
	// ****************************************************

	// 前m/2+1行
	i = 1;
	for(j = 0; j < m/2; j+=2, i+=2)
	{
		for(k = m/2-j; k < m; k++ )
		{
			cov[i] += data[k-(m/2-j)] * g[k];   // k针对core[k]
		}

		for(k = n-m/2+j; k < n; k++ )
		{
			cov[i] += data[k] * g[k-(n-m/2+j)]; // k针对data[k]
		}
	}

	//中间的n-m行
	for( ; i <= (n-m)+m/2; i+=2)
	{
		for( j = 0; j < m; j++)
		{
			cov[i] += data[i-m/2+j] * g[j];
		}
	}

	// 最后m/2-1行
	// i = ( (n - m) + m/2 + 1 );
	for(j = 1; j <= m/2; j+=2, i+=2)
	{
		for(k = 0; k < j; k++)
		{
			cov[i] += data[k] * g[m-j-k];     // k针对data[k]
		}

		for(k = 0; k < m-j; k++)
		{
			cov[i] += g[k] * data[n-(m-j)+k]; // k针对core[k]
		}
	}
}

/*****************************************************************
*	函数: 排序函数
*
*	说明: 将卷积后的结果data[]进行排序，使尺度系数和小波系数分开
*****************************************************************/
void Sort(double data[], double sort[], int n)
{
    int i;
	for(i = 0; i < n; i+=2) // 上采样
	{
		sort[i/2] = data[i];
	}

	for(i = 1; i < n; i+=2) // 下采样
	{
		sort[n/2+i/2] = data[i];
	}

}

/*****************************************************************
*　函数: 一维小波变换函数
*
*　说明: 一维小波变换,可进行多次分解　
*
*　输入参数: input[],   输入信号; 
*            output[],  小波变换结果，包括尺度系数和小波系数两部分; 
*            temp[],    存放中间结果;
*            h[],       Daubechies 3 小波基低通滤波器系数;
*            g[],       Daubechies 3 小波基高通滤波器系数;
*            n,         输入信号长度; 
*            m,         Daubechies 3 小波基紧支集长度; 
*            nStep,     小波变换分解次数
*****************************************************************/
void DWT1D(double input[], double output[], double temp[], double h[], double g[], int n, int m, int nStep)
{
	int i = 0;

	for(i = 0; i < n; i++)
	{
		output[i] = input[i];
	}

	for(i = 0; i < nStep; i++)
	{
		Covlution(output, h, g, temp, n, m);
		Sort(temp, output, n);
		n = n/2;
	}
}

void main()
{

	double data[LENGTH];        // 输入信号
	double temp[LENGTH];        // 中间结果
	double data_output[LENGTH]; // 一维小波变换后的结果

	int i = 0; 
	int n = 0;                        // 输入信号长度
	int m = 6;                        // Daubechies 3 正交小波基长度
	int nStep = 1;                    // 分解级数

	static double h[] = {.332670552950,
		                 .806891509311,
						 .459877502118, 
						-.135011020010,
						-.085441273882,
					     .035226291882};

	static double g[] = {.035226291882,
		                 .085441273882,
						-.135011020010, 
						-.459877502118,
						 .806891509311,
						-.332670552950};

	 char data1[LENGTH];              // 缓冲区, 从txt文件中读取一行数据
	 FILE *fp;                        // 文件指针
	 int len;                         // 行字符个数
	 if((fp = fopen("D:\\data.txt","r")) == NULL)
	 {
		 perror("fail to read");
		 exit (1) ;
	 }
	 
	 while(fgets(data1,LENGTH,fp) != NULL)
	 {
		 data[n] = atof(data1);
		 n++;

		 len = strlen(data1);
		 data1[len-1] = '\0';         // 去掉换行符
		 printf("%s %d \n",data1, n); // 打印文件中每行字符串及文件中总字符串个数
	 }
	 
	 // 打印从文件中读取的数值
	 /*for(i = 0; i < LENGTH; i++)
	 {
		 printf("%.12f\n",data[i]);
	 }*/

	// 一维小波变换
	DWT1D(data, data_output, temp, h, g, n, m, nStep);

	// 一维小波变换后的结果写入txt文件
	fp=fopen("D:\\data_output.txt","a");


	// 打印并写入一维小波变换后的结果
	for(i = 0; i < n/pow(2,nStep-1); i++)
	{
		printf("%f\n", data_output[i]);
		fprintf(fp,"%f\n", data_output[i]);
	}

	// 关闭文件
	fclose(fp);
}

2. 代码效果验证程序（MATLAB）

代码如下：

%% 2022.04.30晚
%  目的：将Visual C++ 6.0 代码中运算得到的数据
%  与matlab自带的小波分解和重构函数得到的数据做对比分析；
%% 导入原始信号并利用matlab自带分解函数得到近似及细节系数
load leleccum;
s = leleccum(1:4320);

% 采用matlab自带函数
[cA1,cD1] = dwt(s,'db3');

%% Visual C++ 6.0 代码中运算得到的数据（近似及细节系数）
Data_Output = load('D:\data_output.txt');

Num = length(Data_Output);

data_output_L = Data_Output(1:Num/2);     % 近似系数（低频）
data_output_H = Data_Output(Num/2+1:4320);% 细节系数（高频）

%% 两种方法获得的近似及细节系数对比分析
figure(1); % 近似系数对比
plot(data_output_L,'black');
hold on
plot(cA1,'r');
legend('data_output_L','cA1');            % 添加线段标签

figure(2); % 细节系数对比
plot(data_output_H,'black');
hold on
plot(cD1,'r');
legend('data_output_H','cD1');            % 添加线段标签

%% 将Visual C++ 6.0 代码中运算得到的数据（近似及细节系数）重构后与原始数据作对比
A1 = upcoef('a',data_output_L,'db3',1);
D1 = upcoef('d',data_output_H,'db3',1);

figure(3); % 重构后与原始数据作对比
plot(A1+D1,'black');
hold on
plot(s,'r');
legend('A1+D1','s');            % 添加线段标签

---

三、代码效果验证展示

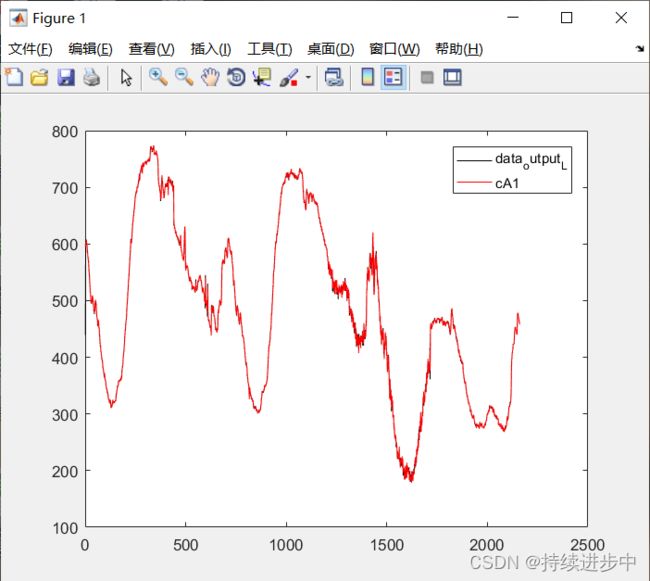
1. 近似系数对比

2. 细节系数对比

3. 重构后与原始数据对比

---

总结

1） 介绍了代码实现和验证工具并提供了下载渠道；
2） 基于原代码进行适当修改并在Visual C++ 6.0上编译实现；
3） 为验证代码效果，在MATLAB中与dwt函数获得的结果进行比较分析；
4） 结果显示，所写代码能较好实现对原始信号的分解。

---

参考

https://blog.csdn.net/lichengyu/article/details/5829785
https://blog.csdn.net/Archar_Saber/article/details/50043507
baike.baidu.com/item/MATLAB/263035
https://blog.csdn.net/GGY1102/article/details/121733746
https://blog.csdn.net/chengxiao_ling/article/details/88993680