Spark MLlib 源码学习---朴素贝叶斯模型(Naive Bayes)

朴素贝叶斯是机器学习中比较常用的一种模型，尤其在文本分类的问题上是比较常用的baseline。朴素贝叶斯本身训练速度快，具有可并行化程度高，可解释性好的优点，但由于其对特征之间的独立性假设不是很符合某些需求场景，因此在实际的使用过程中往往需要做一些特征组合的预处理工作来提升模型的效果。目前，很多的机器学习开源项目都支持了朴素贝叶斯，比如Python的Scikit-Learn和NLTK。Java项目中Weka、Smile、Apache Ignite中Machine Learning库还有就是这里介绍的Spark ML/MLlib库。下面先介绍下Naive Bayes模型及其变种的基本原理，然后结合例子来简单分下下源码实现。

0. 朴素贝叶斯基本原理

朴素贝叶斯是基于贝叶斯定理的一种生成式模型。贝叶斯公式如下：

$$formula1：P(Y|X)=\frac{P(Y)\ast P(X|Y)}{P(X)}=\frac{P(Y)\ast P(X|Y)}{{\sum }_{j=1}^{M}P(Y_j)\ast P(X|Y_j)}$$

$X=(x_1,x_2,...,x_N)$代表的是$N$维的特征向量，$Y=(y_1,y_2,...,y_M)$代表的是$M$维的标记空间，假设特征之间相互独立，那么就有如下关系：

$$formula2:P(X|Y)=P(x_1|Y)\ast P(x_2|Y)\ast ...\ast P(x_N|Y)=\prod _{i=1}^{N}P(x_i|Y)$$

这个独立性假设也是该模型中朴素二字的由来。很多时候，这种假设是过于苛刻甚至是不符合实际情况的，但在实际应用的效果还是相当不错的，是一种能够快速落地的基准模型。
从$formula1$中可以知道，在预测某个具体的实例时，我们关心的其实只是分子部分的结果，分母部分是一致的，无需比较。因此，对于朴素贝叶斯模型的时候，模型需要估计的参数其实只有$P(Y)$和$P(X|Y)$两个，通常我们可以用$\pi$和$\theta$来表示。参数$\pi$是一个向量，如：${\pi }_i=P(Y=y_i)$表示每个类别的先验概率，参数$\theta$是一个矩阵，如：${\theta }_{i,j_l}=P(X=x_{j_l}|Y=y_i)$。这里的$x_{j_l}$代表的是某一个特征维度的具体取值，如西瓜书中，"色泽"特征的枚举值为{青绿，乌黑，浅白}，所以$x_{j_l}$就可以代表“色泽=青绿，色泽=乌黑，色泽=浅白”三种取值方法中的任意一种。在实际的工程实现中，往往将每个枚举值作为一个独立的特征对待，就像“色泽=青绿，色泽=乌黑，色泽=浅白”是作为三个独立的特征来处理的，因此${\theta }_{i,jl}$可以转化为为${\theta }_{i,j}$。

基于极大似然的参数估计，可以知道$\pi$和$\theta$两个参数的计算方法为：
$$formula3:{\pi }_i=\frac{Count(Y=y_i)}{D},s.t.\sum _{i=1}^M{y}_i=D$$
其中$D$表示训练集的大小。
$$formula4:{\theta }_{i,j}=\frac{Count(Y=y_i,X=x_j)}{Count(Y=y_i)}$$
朴素贝叶斯模型的训练过程也就是基于上述公式计算$\pi$和$\theta$的过程。在此基础上，我们可以计算待预测的实例相对于所有类别的后验概率，并选择最大后验概率的类别作为预测结果。假设待预测实例的特征向量为$\lambda =({\lambda }_1,{\lambda }_2,...,{\lambda }_N)$,预测结果则有：
$$formula5:y=\mathrm{argmax}(\theta \ast \lambda )⨀\pi ,\theta <>0$$
这里的$⨀$运算符表示element-wise的乘积操作，也就是所谓的Hadamard Product。对于所有类别，分别计算待预测实例中涉及到特征的联合概率，由于之前提到的独立性假设，因此直接计算他们的乘积即可。最后再计算与类别自身先验概率的乘积，就可以得到该实例分到所有类别下的概率值，并选择最大值最为分类结果。
需要说明的是，对于待预测实例中出现了新特征时，会出现${\theta }_{i,j}=0$的情况，这样会导致联合概率值等于0的情况，因此在工程实践中往往需要考虑对这样的特征做平滑处理。常见的就是Add-One Smoothing，也就是所谓的Laplace Smoothing。这个在下面介绍Spark中的Naive Bayes实现的时候再具体说明。
常见的朴素贝叶斯主要有多项式型(Multinomial)和伯努力型(Bernoulli)。多项式型朴素贝叶斯模型考虑每个特征的权重值，比如文本分类问题中每个词的词频或者TF-IDF值。而相对的，伯努利型朴素贝叶斯模型则不考虑每个特征值的权重，也就是说只考虑某个特征是否出现。对于连续型特征，还可以使用高斯型(Gaussian )贝叶斯模型。在Spark 3.x版本的ML库中，除了以上三种朴素贝叶斯模型以外，还实现了补码(Complement)朴素贝叶斯模型。补码朴素贝叶斯模型是多项式型的一种变体，比较适合处理样本不均衡的分类问题。由于MLlib库目前处于维护的状态，因此3.x版本中依然只支持多项式型和伯努利型两种。下面我们通过一个例子来介绍如何使用ML/MLlib中的Naive Bayes模型来处理文本分类的问题。

1.朴素贝叶斯建模文本分类问题

在Deeplearning4j实战的专栏中，写了两篇分别基于LSTM和CNN的文本分类的文章，当时使用的语料是《科学空间》系列博客的作者苏剑林老师在他的一篇博客中分享出来的。语料规模不是很大，主要是关于商品评价的短文本，很适合一些模型原型验证阶段时候使用，因此这里我还是继续使用该语料库。有需要的同学可以直接访问苏老师的博客：科学空间–文本情感分类。部分语料截图如下。

我们使用HanLP对语料进行分词处理。部分分词结果如下。

经过统计，总共有4W+个中文词。此外，我们还分别统计了在每条语料中各个中文词的词频作为权重值，使用了自增索引作为每个词的特征索引。通过简单逻辑转换，将原始语料库转化为libsvm格式的训练集。截图如下。

截图中的第一列是每条文本的标注，之后的每一列都是{词索引}:{词频}。下面是基于ML库中提供的朴素贝叶斯模型建模的过程。

import org.apache.spark.ml.classification.{NaiveBayes,NaiveBayesModel}
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator

import org.apache.spark.sql.SparkSession

class NaiveBayesExample{
  
}

object NaiveBayesExample {
    def main(args : Array[String]) : Unit = {
      val spark = SparkSession.builder().appName("NB ML").getOrCreate()
      spark.sparkContext.setLogLevel("DEBUG")//设置DEBUG日志级别
      val data = spark.read.format("libsvm").load("corpus/corpus.txt")
      
      //交叉验证，70%训练集，30%验证集
      val Array(trainingData, testData) = data.randomSplit(Array(0.7, 0.3), seed = 1234L)
      
      //朴素贝叶斯超参数设置以及训练
      val model:NaiveBayesModel = new NaiveBayes()
                  .setModelType("multinomial")  //multinomial,bernoulli,complement,gaussian 
                  .setSmoothing(1.0)  //平滑参数，0.0~1.0
                  .fit(trainingData)
      val numClasses : Int = model.numClasses
      val numFeatures : Int = model.numFeatures
      val testDataSize = testData.count()
      //打印训练集的信息
      println(s"test data size: $testDataSize, Number of Labels: $numClasses, Number of Features: $numFeatures")
      val predictions = model.transform(testData)
      //验证集进行评估
      val evaluator = new MulticlassClassificationEvaluator()
        .setLabelCol("label")
        .setPredictionCol("prediction")
        .setMetricName("accuracy")
      val accuracy = evaluator.evaluate(predictions)
      println(s"Test set accuracy = $accuracy")
    }
}

我们使用DataFrameReader直接加载libsvm格式的训练数据，然后随机按照7：3的比例划分训练集和验证集。在设置模型的超参数的时候，主要涉及模型类型和平滑系数。上面的逻辑中模型类型使用的是多项式型，是ML库中默认的朴素贝叶斯变体类型，平滑系数设置成1.0，这也是默认的平滑系数。调用fit方法来训练朴素贝叶斯模型。待训练完毕后，我们打印一些模型的基本信息，包括分类和特征的数量。

最后，在验证集上对模型的效果进行评估。评估结果如下。

总体的准确率在82.5%左右，应当是并不是非常出色。但考虑到我们没有做非常细致的特征清洗，包括停用词等预处理工作并没有做，因此这样的结果还是勉强能够接受，作为一个基准模型是完全可以的。下面我们来分析下Spark ML/MLlib中朴素贝叶斯的实现。

2.Spark ML/MLlib源码分析

Spark ML和MLlib库都支持朴素贝叶斯模型。MLlib是Spark早期重点支持的机器学习库，大多都直接基于RDD作为底层计算的数据模型包括作为接口的出参和入参。ML库是目前Spark主要支持的机器学习库，是基于DataFrame/DataSet数据模型的来实现的，并提供了Pipeline方便特征预处理、建模和模型评估这完整的机器学习工具栈，这也是参考了scikit-learn的实现。从2.x开始MLlib库开始进入维护的状态，并且很多内部实现都逐渐迁移到ML库，也包括这里说的朴素贝叶斯模型。下面我们分别来看下朴素贝叶斯四种变体的源码实现方式，主要以ML库的实现为主。

2.1 多项式型朴素贝叶斯（Multinomial NB）

2.1.1 参数估计和平滑

上文中提到，朴素贝叶斯的训练就是$\pi$和$\theta$这两个参数估计的过程。对于多项式朴素贝叶斯而言，则有：
$${\pi }_i=\frac{Count(Y=y_i)+\alpha }{D+\alpha M},s.t.\sum _{i=1}^M{y}_i=D$$
$${\theta }_{i,j}=\frac{Freq(x_j,y_i)+\alpha }{{\sum }_{j=1}^{N}Freq(x_j,y_i)+\alpha N}$$
参数$\pi$的计算方式和上面描述的是一致的，而$\theta$的计算方式有些细微的不同，在$formula4$中的$Count$函数这里用特征频率值来表征，分子中的$Freq(x_j,y_i)$表示在第$i$个类别中第$j$个特征出现的总数。当然这里的$Freq$函数的物理意义可以是单纯的频次，也或者是诸如TF-IDF等计算结果。分母中的${\sum }_{j=1}^{N}Freq(x_j,y_i)$表示第$i$个类别中所有特征的频数总和。公式中的$\alpha$是平滑系数，一般取值范围为$0<\alpha <1$。一般情况下，$\alpha$的取值为1即可。我们来看下ML库中的实现。

2.1.2 $\pi$和$\theta$参数的计算

ML库中朴素贝叶斯模型训练的实际入口方法是NaiveBayes.trainWithLabelCheck。该入口方法的入参其中一个是DataSet形式的带标注的训练数据集，另一个布尔类型的参数则是用于兼容MLlib的老逻辑。这里不展开细说了，该方法的注释里有清晰的解释。第158-168行是该入口方法的核心部分，对于不同类型的朴素贝叶斯模型调用不同的实现方法来计算$\pi$和$\theta$两个参数。除了用于连续特征的高斯型朴素贝叶斯模型调用NaiveBayes.trainGaussianImpl方法外，多项式型、伯努利型还有补码朴素贝叶斯模型都是调用NaiveBayes.trainDiscreteImpl方法。我们来分析下NaiveBayes.trainDiscreteImpl方法的实现。L174-187的部分声明了一个UDF函数，主要功能是对除了高斯型的朴素贝叶斯模型变体进行特征值合法性的校验，例如Bernoulli型的特征值必须是非0即1。另外一部分逻辑是创建一个样本权重的列，如果原先就设置了样本权重，则仅仅做个数值类型转换即可，否则样本权重全部设置为默认值1。L188-L203的部分是对训练集进行聚合处理，先看下代码截图。

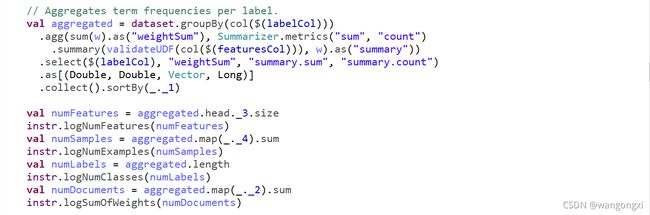
对象dataset中主要包含两列label:Double和features:Vector，这个和MLlib使用LabeledPoint是一致的。首先基于label值对dataset数据集进行分组，然后针对每个分组，也就是分布在每个label值下的样本实例进行特征的聚合计算。在聚合的过程中，会调用ml库的统计工具包Summarizer来计算特征向量的中每个特征值的和以及总数量，同时使用上面声明过的UDF函数进行特征值的校验，并最终得到选择标注(label)、样本权重累加值(weigthSum)、特征向量聚合值(summary.sum)还有样本数量(summary.count)这四列。再做了数据类型转换后，通过collect算子将结果收集到driver主节点上，并基于label的取值大小做了排序。后面的几行代码主要是收集一些训练样本的信息，比如特征数量、样本总量等并加以记录日志。

上面截图中的三行代码声明了之前说过的$\pi$、$\theta$参数以及一个用于记录label值的数组。$\theta$参数这里用的数组，到最终保存到NaiveBayesModel的成员变量值的时候，会转化成Matrix的形式。L208-L222对于多项式型的朴素贝叶斯模型没有特殊处理，这里直接略过，我们直接看L222-L242部分对于两个参数的计算。先附上代码片段。

在2.1.1中我们给出了两个参数的计算方式。需要说明的是，在算法工程实现时为了缓解计算机数值计算可能的溢出问题，通常会用取对数的方式将数值的乘积运算转化为数值的累和运算，在保证相关性的同时缓解了数值溢出的问题。我们将2.1.1中两个参数的计算方法直接取对数，就是得到下面两个公式。
$${\pi }_i=log(Count(Y=y_i)+\alpha )-log(D+\alpha M),s.t.\sum _{i=1}^M{y}_i=D$$
$${\theta }_{i,j}=log(Freq(x_j,y_i)+\alpha )-log(\sum _{j=1}^{N}Freq(x_j,y_i)+\alpha N)$$
再回到上面的代码片段中。piLogDenom对应的就是参数$\pi$计算公式中的减数部分，lambda则是平滑系数，对应公式中的$\alpha$。接着对aggIter对象进行遍历。上面已经提到，aggIter中的每个对象都是一个四元组，包含标注(label)、样本权重累加值(weigthSum)、特征向量聚合值(summary.sum)还有样本数量(summary.count)这四个部分。对aggIter的遍历其实是对于每个label下的样本计算模型参数。对于参数$\pi$，直接取四元组中的第二个元素(并加上平滑系数)取对数后，减去之前算好的piLogDenom就可以得到当前label的先验概率值。类似的，对于$\theta$参数，也是先计算对数公式中的第二部分的值。对于多项式型，可以参考公式中的描述即将该label下的所有的特征取值累加起来并加上平滑项后再取对数。代码实现中，由于之前已经到label维度聚合了各个特征的累加值，因此只需要取出四元组中的第三个对象(是一个Vector对象)，并将该对象中的所有值累加起来就可以得到label下所有特征值的累和。然后加上平滑系数并取对数，即可得到公式中的第二部分的取值。接着对于每一个特征，我们计算公式中第一项的值，也就是被减数的值。代码中只要对于四元组中第三个元素根据下标进行索引即可得到该特征的所有样本的累计值。同样，加上平滑系数后取对数，就能得到公式中的第一部分，再减去之前算好的第二项，即为当前$\theta$参数的值。根据上面描述的计算过程，将aggIter对象遍历完，两个模型的参数就计算好了。
最后L242-L254部分是将两个参数的类型转化为Vector和Matrix，这里就不多赘述了。

2.1.3 预测逻辑的实现

在2.1.2的基础上，我们会得到一个NaiveBayesModel的实例对象，这个对象的主要成员变量就是上面说的$\pi$和$\theta$两个参数。可以看下截图。

$\sigma$参数是高斯型朴素贝叶斯模型中会涉及，这个在2.4.2的部分会提到。
我们可以调用NaiveBayesModel.predict系列方法预测单个实例的分类结果，也可以调用transform方法进行批量预测，不过内部也是调用predict方法来预测。模型预测的实际入口方法是NaiveBayesModel.predictRaw。我们看下代码截图。

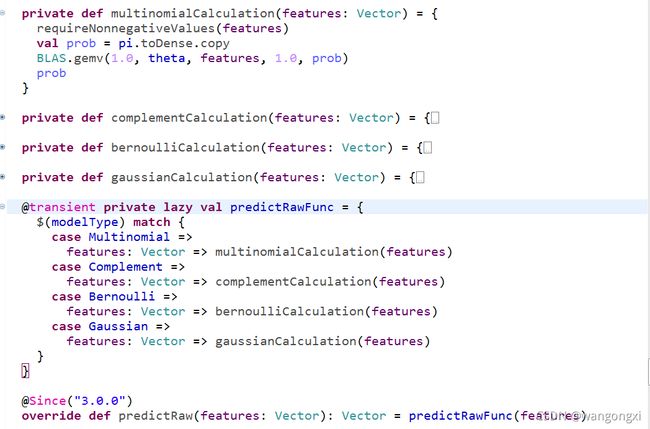
对于目前Spark中支持的四种朴素贝叶斯变体分别定义了各自的预测方法。截图中最上方的就是针对于多项式型朴素贝叶斯的预测逻辑。应当说逻辑非常清晰。首先对待预测实例的做特征值合法性的校验，然后调用BLAS.gemv方法计算预测实例分到每个label下的概率大小。对上面$formula5$中计算特征对应每个label概率的部分取对数，可得到：
$$y=\mathrm{argmax}log((\theta \ast \lambda )⨀\pi )=\mathrm{argmax}(log(\theta \ast \lambda )+log(\pi ))$$
由于之前已经进行了对数几率的计算，因此在源码实现的时候就直接调用了gemv方法。需要注意的是，这里计算出来的该实例对于每个label下的概率只是没有规范化的对数几率，并不是真正概率值。这从方法的命名上也可以看出是raw probability。如果只是要得到分类结果的相对概率大小，可以直接将raw probability排序。如果需要得到准确的概率值大小，则需要调用NaiveBayes.raw2probabilityInPlace进行转化。可以看如下截图。

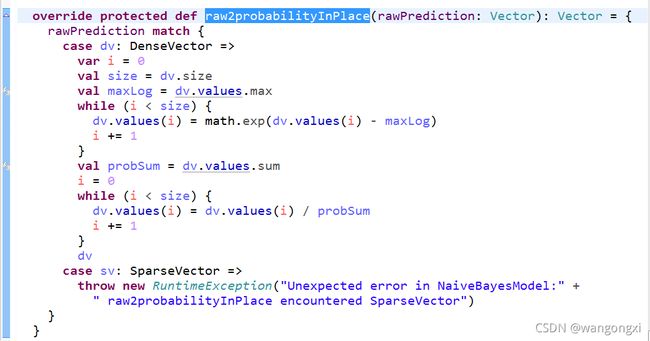
NaiveBayes.raw2probabilityInPlace方法中主要分为两部分逻辑。第一部分是将对数几率通过指数函数还原后进行最大值归一化处理，然后再计算归一化各个值的占比。

2.2 伯努力型朴素贝叶斯（Bernoulli NB）

2.2.1 参数估计和平滑

对于伯努力型朴素贝叶斯而言，参数的计算方法如下：
$${\pi }_i=\frac{Count(Y=y_i)+\alpha }{D+\alpha M},s.t.\sum _{i=1}^M{y}_i=D$$
$${\theta }_{i,j}=\frac{DocCount(X=x_j,Y=y_i)+\alpha }{DocCount(Y=y_i)+2\alpha }$$
对比于多项式型朴素贝叶斯，参数$\pi$的计算没有变化，而$\theta$的计算方式不同。对于伯努力型而言，参数$\theta$的分母部分是某个具体label值在总的样本中出现的数量，而分子部分是在该label值的样本中某个具体特征出现的样本数量。由于伯努力型朴素贝叶斯模型中，特征值的取值非0即1，因此分子部分的值其实也是某个具体特征在某个label下频率总和，从这个意义上讲，分子部分和多项式型是一致的。下面来看下具体的计算过程。

2.2.2 $\pi$和$\theta$参数的计算

参数$\pi$的计算和多项式型朴素贝叶斯的计算过程一致，这里就不赘述了。我们主要看下$\theta$参数的计算。先看下代码的截图。

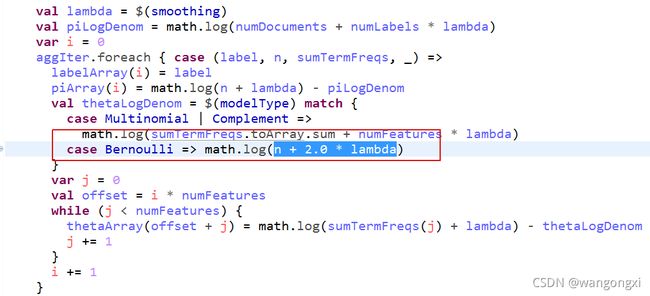
截图中红框中标识的是参数$\theta$分母的部分。其中变量n是该label的样本数量，加上平滑系数后取对数值。然后在while循环中对于每个特征，计算在该label下的后验概率值。在2.2.1中说明过，对于伯努力型而言，出现某个特征的样本数量等同于该特征的频率和，因此这里沿用多项式型中的计算方式。

2.2.3 预测逻辑的实现

对于伯努利型朴素贝叶斯模型，特征的后验概率服从伯努利分布，即可统一为：
$$P(x_i|y_j)=\{\begin{array}{l}{\theta }_{i,j},x_i=1\\ 1-{\theta }_{i,j},x_i=0\end{array}={\theta }_{i,j}\ast x_i+(1-{\theta }_{i,j})\ast (1-x_i),s.t.x_i\in \{0,1\}$$
在2.2.2部分已经介绍了参数$\theta$和$\pi$的计算过程，为了在最后计算各个类别概率时候和多项式分布统一，Spark源码中对参数$\theta$和$\pi$做了进一步的处理。

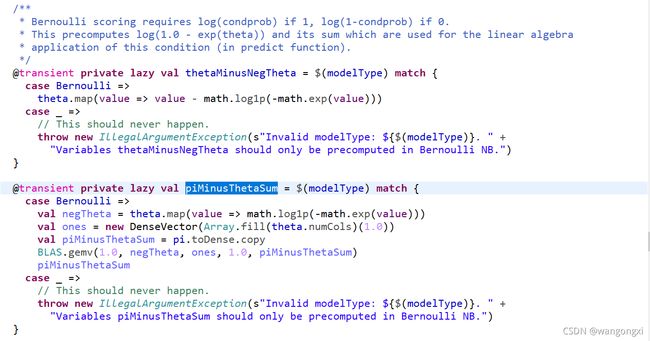
在这两个方法开始的注释上已经做了一些解释，首先时伯努利分布条件下，在特征值分别取0或1的条件下，概率取值的关系，这在上面的公式中已经说明，只不过这里时先取了对数机率。两个方法的作用可以用以下关系概括：
$${\theta }_i:=log{\theta }_i-log(1-{\theta }_i)$$
$${\pi }_j:={\pi }_j+\sum _{i=1}^{N}log(1-{\theta }_i)$$
这就是piMinusThetaSum和thetaMinusNegTheta计算的逻辑。
在实际计算每个类别的概率时有：
$$y_j={\pi }_j+\sum _{i=1}^{N}log(1-{\theta }_i)+\sum _{i=1}^N{\lambda }_i\ast (log{\theta }_i-log(1-{\theta }_i)),s.t.{\lambda }_i\in \{0,1\}$$
对应于源码中的实现如下截图：

2.3 补码朴素贝叶斯（Complement NB）

2.3.1 参数估计和平滑

补码朴素贝叶斯是多项式型的变体。对于多项式型来说，参数$\theta$计算的是特征从属于各个类别的后验概率。而对于补码朴素贝叶斯来说，$\theta$计算的是特征不属于某个类别的概率，是一种逆向的计算方式。在预测实例的阶段，也是将概率最小的不从属的类别作为分类结果。更多内容可以参考Complement NB的论文。
$${\theta }_{i,j}=\frac{Freq(X=x_j,Y\ne y_i)+\alpha }{{\sum }_{j=1}^{N}Freq(X=x_j,Y\ne y_i)+\alpha N}$$
上面公式是补码朴素贝叶斯参数$\theta$的计算逻辑。至于完整的补码朴素贝叶斯训练与预测的计算流程，我们给出论文中的描述的过程。

其中截图中第四部对应的是上面给出的公式。5_{6两步是对参数$\theta$取对数后再做规范化处理。7}8是描述预测过程的计算逻辑，直接将规范化后的参数$\theta$与特征向量作内积。需要注意的是，最终并不是取$\mathrm{argmax}$的结果，而是取$\mathrm{argmin}$的结果作为预测值。原因也是之前说过的，补码朴素贝叶斯的参数计算的是某个特征不从属于当前类别的概率，因此在预测的时候，这个**“不属于”的值越小，则反过来"属于"**的概率就越大。

2.3.2 $\pi$和$\theta$参数的计算

参数$\pi$的计算和多项式型的计算逻辑相同，但实际在预测阶段并没有使用到参数$\pi$，原因的话在论文中有一段解释。

论文中的意思大致是参数$\pi$的值在预测过程中往往无法左右最终的预测结果，起到主导地位的还是参数$\theta$，因此直接就忽略了它。其实我个人认为还有一个原因，就是在样本不均衡的情况下，参数$\pi$的融入可能会导致预测结果的进一步偏差，因此这里就不考虑了。接着我们看下$\theta$的计算。

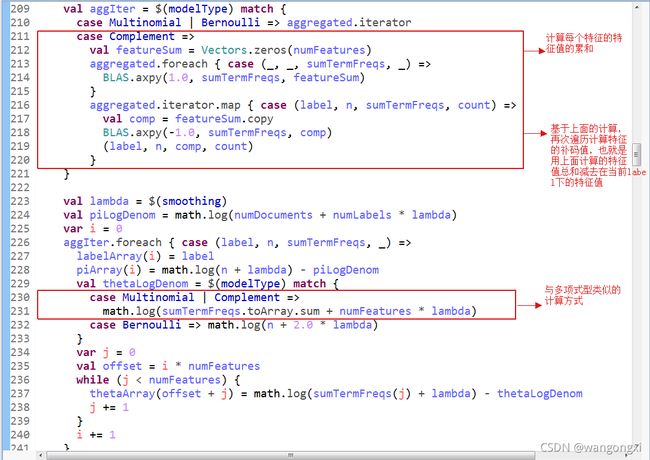
为了方面说明在截图中已经给出了部分的说明。第一个红框实际计算的是2.3.1中给出的$\theta$计算公式的分子的部分，也就是每个特征不从属于当前label的特征值的总和。第二个红框就是分母部分的计算。由于取了对数，因此最后在给$\theta$的每个元素赋值的时候，都转化成了减法运算。

为了和多项式型以及伯努力型统一预测的计算逻辑，在保存到模型成员变量中的时候，$\theta$中的每一个值都作为取反运算。

2.3.3 预测逻辑的实现

补码朴素贝叶斯的预测逻辑在NaiveBeyesModel.complementCalculation方法中实现。论文中给出了label预测的计算方法，这在2.3.1部分中已经提到。我们给出NaiveBeyesModel.complementCalculation的代码片段。

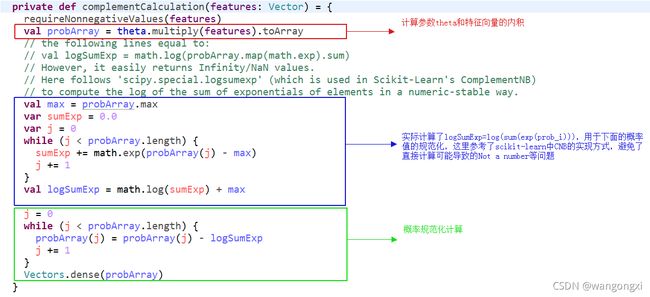
补码朴素贝叶斯的预测逻辑主要有两个部分，首先计算特征向量和参数$\theta$的内积，然后将得出的值做下规范化处理。规范化因子计算的是所有后验概率加和的对数值，即$logSumExp=log{\sum }_{i}exp(pro{b}_i)$，实际在计算规范化因子，也就是截图中的logSumExp值的时候，参考scikit-learn的scipy.special.logsumexp的实现方式，防止了数值异常的情况出现。
需要注意的是，由于参数$\theta$在训练阶段实际最终取的是真实值的相反数，因此和多项式型以及伯努力型一样取概率值最大的那个类别作为预测结果，而不是概率值最小的那个类别。

2.4 高斯朴素贝叶斯（Gaussian NB）

2.4.1 参数估计和平滑

高斯型朴素贝叶斯主要应用于连续型特征的建模。模型假设label下的特征取值服从高斯分布，即：
$$P(x_i|y_j)=\frac{1}{\sqrt{2\pi {\sigma }_j^2}}exp(-\frac{(x_i-{\mu }_j{)}^2}{2{\sigma }_j^2}),{\mu }_j=\frac{{\sum }_{i=1}^N{x}_{i,j}}{N},{\theta }_j^2=\frac{{\sum }_{i=1}^N(x_{i,j}-{\mu }_j{)}^2}{N}$$
高斯函数中涉及到两个参数$\mu$和$\sigma$，也就是均值和方差，它们同时也是高斯型朴素贝叶斯的两个需要训练的参数，这和上面所讨论的模型参数是不同的。

2.4.2 参数$\pi$，$\mu$和${\sigma }^2$的计算

高斯型朴素贝叶斯参数计算的实际入口是NaiveBayes.trainGaussianImpl这个方法。与trainDiscreteImpl方法类似，trainGaussianImpl方法共分为样本权重计算、样本分组聚合计算、平滑参数$ϵ$计算以及$\pi$,$\mu$,${\sigma }^2$三个参数的计算这几个步骤。样本权重和trainDiscreteImpl相同，一般在不设置的情况下默认权重都是1.0。在样本的分组聚合过程中，首先根据label的取值对样本进行分组，然后计算在每个label下所有样本特征的均值和L2范数值($||x_i|{|}_2=\sqrt{{\sum }_{i=1}^N{x}_i^2}$)。为了方便下面计算每个特征的方差，因此直接计算L2范数的平方($||x_i|{|}_2^2={\sum }_{i=1}^N{x}_i^2$)。接着是计算平滑系数$ϵ$，主要为了解决某些特征维度方差过小的问题，具体参考了scikit-learn的实现，这里不多赘述，有兴趣的同学可以看下代码细节。最后来看下$\pi$,$\mu$,${\sigma }^2$三个参数的计算。看下下面的截图。

参数$\pi$的计算同之前介绍的其他朴素贝叶斯的变体，也就是每个label下的样本数量占总样本数的比率。$\mu$和${\sigma }^2$分别使用代码截图中的thetaArray和sigmaArray两个变量来进行存储。由于特征的均值在样本分组聚合的步骤中已经计算好了，因此直接赋值给thetaArray中元素即可。参数${\sigma }^2$的计算是基于${\sigma }^2=E(X^2)-E^2(X)$来得到，其中$E(X^2)$是通过特征值的L2范数除上以总的样本数量，$E^2(X)$则是均值的平方，两者的差值再加上平滑系数就得到了参数${\sigma }^2$的值。最后将三个参数保存到NaiveBayesModel的成员变量中即可。

2.4.3 预测逻辑的实现

根据$formula2$再结合高斯朴素贝叶斯的特点，我们可以做如下推导。
$log(P(X|Y=y_j))=log({\prod }_{i=1}^{N}P(x_i|Y=y_j))={\sum }_{i=1}^{N}log(x_i|Y=y_j)={\sum }_{i=1}^{N}log(\frac{1}{\sqrt{2\pi {\sigma }_j^2}}exp(-\frac{(x_i-{\mu }_j{)}^2}{2{\sigma }_j^2}))={\sum }_{i=1}^N(-log(\sqrt{2\pi {\sigma }_j^2})-\frac{(x_i-{\mu }_j{)}^2}{2{\sigma }_j^2}))={\sum }_{i=1}^N(-log{\sigma }_j-log(\sqrt{2\pi })-\frac{(x_i-{\mu }_j{)}^2}{2{\sigma }_j^2})=-{\sum }_{i=1}^{N}log{\sigma }_j-{\sum }_{i=1}^{N}log(\sqrt{2\pi })-{\sum }_{i=1}^N\frac{(x_i-{\mu }_j{)}^2}{2{\sigma }_j^2}$
公式中的第一部分也就是源码中的$logVarSum$的值，具体可以看下面截图。

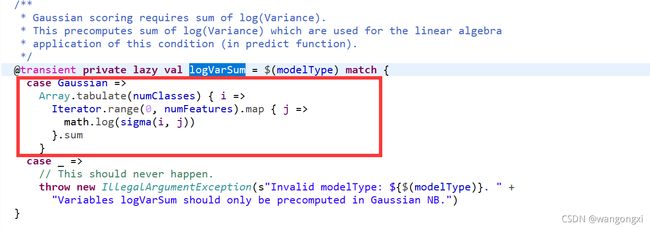
准确来说截图中计算的是${\sum }_{i=1}^{N}log{\sigma }_j^2={\sum }_{i=1}^{N}2log{\sigma }_j$，也就是第一部分值的两倍。这在最后计算的时候会统一处理。

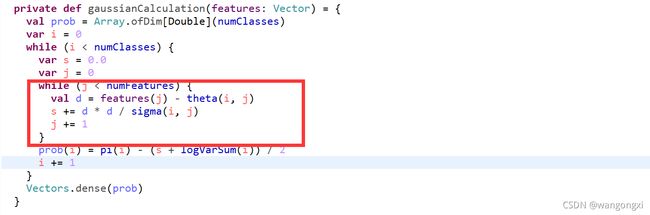
公式中的第三部分在源码中是上面截图中红框截出来的部分，准确来说是${\sum }_{i=1}^N\frac{(x_i-{\mu }_j{)}^2}{{\sigma }_j^2}$，同样在外部的while循环中也做了处理。

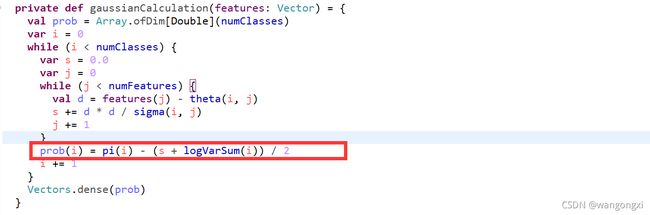
最后这个截图中红框截出来的部分就是上面公式中计算的结果再加上当前label的先验概率，也就是最终分到该label下的对数几率。不过由于公式的第二项是一个对于所有类别都等同的常数，因此实际计算的时候并没有考虑在内，这一点需要注意。
最后做下小结。在Spark中高斯朴素贝叶斯的实现中，并没有直接计算$P(x_i|y_j)$的值作为模型的参数，而是计算高斯分布的均值和方差作为高斯朴素贝叶斯的模型参数，这点和scikit-learn中的实现是不同的，但本质上一样的。

3.总结

这篇博客主要是介绍了Spark ML中支持的四种朴素贝叶斯变体的源码实现。其中高斯朴素贝叶斯主要适用于连续型特征，而其余的三种变体主要用于离散型特征。如果对于同时涉及离散型特征和连续型特征的建模问题，那么目前还无法直接支持，需要做些离散化的操作。当然如果不做离散化，则需要修改下源码来支持混合型特征的建模，具体的可以参考Apache Ignite中Compound Naive Bayes的实现，这里就不多描述了。
Spark中朴素贝叶斯的实现很多地方参考了scikit-learn中的实现方式，包括补码型朴素贝叶斯中$logSumExp$的计算等都是为了防止一些0概率情况下的数值异常错误。当然Spark ML库整体的实现或多或少都参考了scikit-learn的实现，因此两个库有很多相似的地方。
朴素贝叶斯本身是基于特征独立性假设和贝叶斯理论衍生出的算法模型。虽然理论层面有些硬伤，但是不妨碍它在实际生产过程中的广泛应用，包括垃圾邮件分类等等。当然工程师也可以通过组合特征的优化方式来缓解特征独立性假设的缺陷，比如通过$n-gram$语言模型来优化文本类特征。更进一步的，如果我们必须要考虑特征之间的关联关系，则使用贝叶斯信念网络会更合适。
对于上面谈到的4种朴素贝叶斯变体的适用场景，一般来说伯努力型相对于多项式型在不是特别关注特征出现频率的场景下，比如短文本的分类问题中，效果会更优。直观理解就是伯努力型考虑的只是特征是否出现，而不是在同一样本中出现的频率，反之则多项式型更优。对于补码朴素贝叶斯来说，处理样本不均衡问题的效果和鲁棒性会优于多项式型，这个在补码朴素贝叶斯的论文中有分析，感兴趣的同学可以深入研究。
Spark中朴素贝叶斯分布式计算的地方主要是对于特征向量的一些统计结果的分布式计算，比如每一个维度特征的均值和方差等。最终对于模型参数的计算主要都是在driver节点上进行的。因此需要适当调整driver节点的jvm参数来适应在主节点上的计算工作。