基于闪电搜索算法的函数寻优算法
文章目录
- 一、理论基础
-
- 1、闪电搜索算法
- 2、LSA算法流程图
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、闪电搜索算法
闪电搜索算法(Lightning Search Algorithm, LSA)是Shareef H等受自然天气中闪电现象的启发提出的一种优化算法,模拟闪电的快速传播特性,因此收敛速度较快。
LSA是对闪电这种自然现象的观察而得到的新新算法,当闪电形成时,空气中的“放电粒子”与空气碰撞之后会产生一条电离路径或通道,并形成一条梯级先导。LSA算法利用空间放电体、引导放电体等概念建立分布函数模型来求解待解决的问题,空间放电体试图成为最优梯级先导,引导放电体代表种群中的最优个体。
(1)在一个种群规模为 N N N,初始种群的生成服从均匀分布,创建初始随机种群,其概率密度函数 f ( x c ) f(x_c) f(xc)可以表示为 f ( x c ) = { 1 b − a , a ≤ x ≤ b 0 , else (1) f(x_c)=\begin{dcases}\frac{1}{b-a},\quad a\leq x\leq b\\[2ex]0\quad\,\,\,\,\,\,,\quad \text{else}\end{dcases}\tag{1} f(xc)=⎩⎪⎨⎪⎧b−a1,a≤x≤b0,else(1)其中, x c x_c xc是一个候选解, a a a和 b b b分别是“放电粒子”范围的最小值和最大值。
(2)引导放电体表示为 H L H^L HL,由正态概率密度函数 f ( x k ) f(x_k) f(xk)来生成位置 f ( x k ) = 1 σ 2 π e − ( x k − μ ) 2 2 σ 2 (2) f(x_k)=\frac{1}{\sigma\sqrt{2\pi}}e^{\displaystyle\frac{-(x_k-\mu)^2}{2\sigma^2}}\tag{2} f(xk)=σ2π1e2σ2−(xk−μ)2(2)其中, μ \mu μ为形状参数,引导放电体 H L H^L HL在下一次迭代的位置为 H n e w L = H L + n o r m r a n d ( μ L , σ L ) (3) H^L_{new}=H^L+normrand(\mu_L,\sigma_L)\tag{3} HnewL=HL+normrand(μL,σL)(3)其中, n o r m r a n d normrand normrand是正态分布函数生成的随机数, μ L \mu_L μL为形状参数, σ L \sigma_L σL为尺度参数。如果 H n e w L H_{new}^L HnewL的适应度值更优,那么 H L H^L HL更新为 H n e w L H^L_{new} HnewL,否则 H L H^L HL保持不变,直至下一次迭代。
(3)空间放电体可表示 C S = [ c 1 S , c 2 S , ⋯ , c N S ] C^S=[c_1^S,c_2^S,\cdots,c_N^S] CS=[c1S,c2S,⋯,cNS],它的位置服从指数分布,由式(4)决定: f ( x v ) = { 1 μ e − x v μ , x v > 0 0 , x v ≤ 0 (4) f(x_v)=\begin{dcases}\frac1\mu e^{\frac{-x_v}{\mu}},\quad x_v>0\\[2ex]0\quad\quad\,,\quad x_v\leq0\end{dcases}\tag{4} f(xv)=⎩⎪⎨⎪⎧μ1eμ−xv,xv>00,xv≤0(4)形状参数 μ \mu μ会影响 C S C^S CS和 H L H^L HL之间的距离, C S C^S CS在下一次迭代的位置为: C l _ n e w S = C l S ± e x p r a n d ( μ l ) (5) C_{l\_new}^S=C_l^S\pm exprand(\mu_l)\tag{5} Cl_newS=ClS±exprand(μl)(5)其中, e x p r a n d exprand exprand是生成的随机数,服从于指数分布, μ l \mu_l μl为 H L H^L HL与 C S C^S CS之间的距离。如果 C l _ n e w S C_{l\_new}^S Cl_newS有更优的适应度值,那么 C l S C_l^S ClS将被 C l _ n e w S C_{l\_new}^S Cl_newS替代,否则 C l S C_l^S ClS将保持不变。
(4)分叉是放电体的另一特性,在LSA算法中分叉有两种方式,首先分叉会形成两个互相对称的通道: r l = e + g − r l (6) \boldsymbol{r_l}=e+g-r_l\tag{6} rl=e+g−rl(6)其中, e e e和 g g g表示边界, r l r_l rl和 r l \boldsymbol{r_l} rl分别表示原来的通道和分叉产生的对称通道。为了保证种群大小不变,两通道只保留一个。
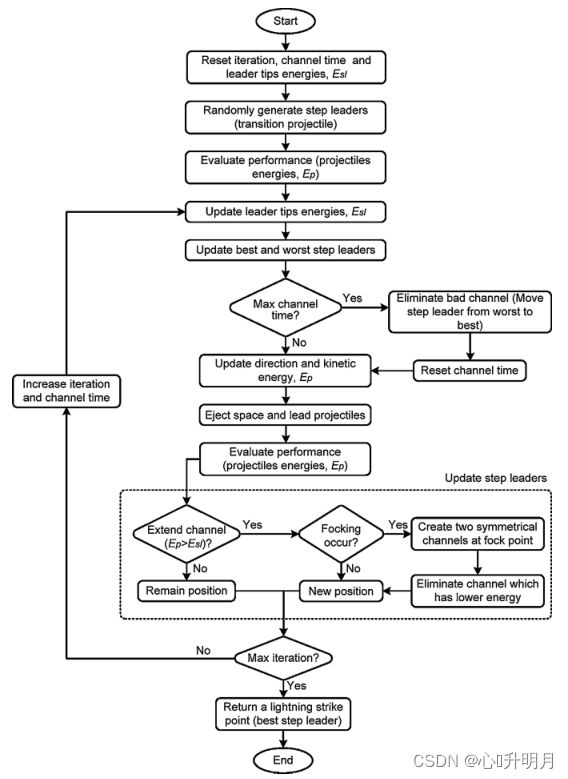
2、LSA算法流程图
二、仿真实验与结果分析
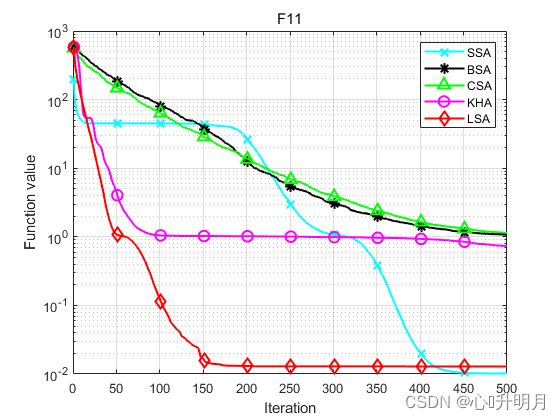
将LSA与SSA、BSA、CSA和KHA进行对比,以常用23个测试函数的F1、F2(单峰函数/30维)、F10、F11(多峰函数/30维)、F18、F19(固定维度多峰函数/2维、3维)为例,实验设置种群规模为50,最大迭代次数为500,每种算法独立运算30次,结果显示如下:
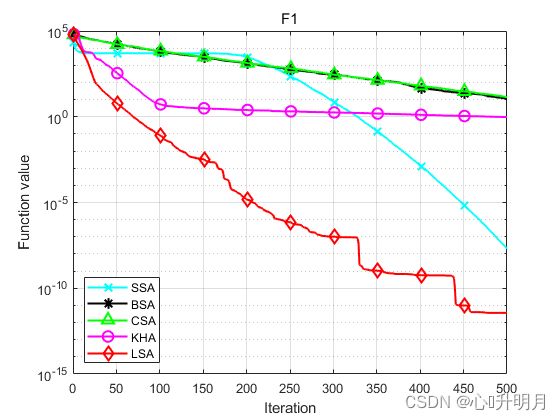

函数:F1
SSA:最差值: 3.27e-08, 最优值: 8.8381e-09, 平均值: 2.0674e-08, 标准差: 5.4715e-09, 秩和检验: 3.0199e-11
BSA:最差值: 43.843, 最优值: 0.92546, 平均值: 11.3774, 标准差: 11.9736, 秩和检验: 3.0199e-11
CSA:最差值: 30.3201, 最优值: 6.1438, 平均值: 13.8803, 标准差: 4.9511, 秩和检验: 3.0199e-11
KHA:最差值: 1.2649, 最优值: 0.4863, 平均值: 0.96054, 标准差: 0.16097, 秩和检验:3.0199e-11
LSA:最差值: 8.1951e-11, 最优值: 3.1043e-19, 平均值: 3.6495e-12, 标准差: 1.5562e-11, 秩和检验: 1
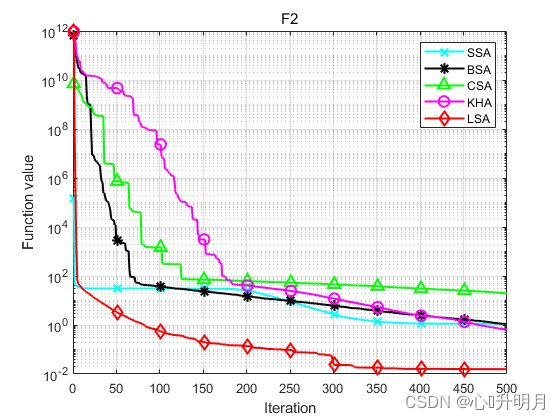
函数:F2
SSA:最差值: 4.904, 最优值: 0.0056029, 平均值: 1.1192, 标准差: 1.1599, 秩和检验: 2.3715e-10
BSA:最差值: 2.1511, 最优值: 0.38432, 平均值: 1.1049, 标准差: 0.38639, 秩和检验: 3.0199e-11
CSA:最差值: 34.6743, 最优值: 11.0359, 平均值: 19.8406, 标准差: 5.4818, 秩和检验: 3.0199e-11
KHA:最差值: 2.7896, 最优值: 0.28697, 平均值: 0.66388, 标准差: 0.49642, 秩和检验:3.0199e-11
LSA:最差值: 0.23313, 最优值: 1.3964e-06, 平均值: 0.015867, 标准差: 0.044386, 秩和检验: 1
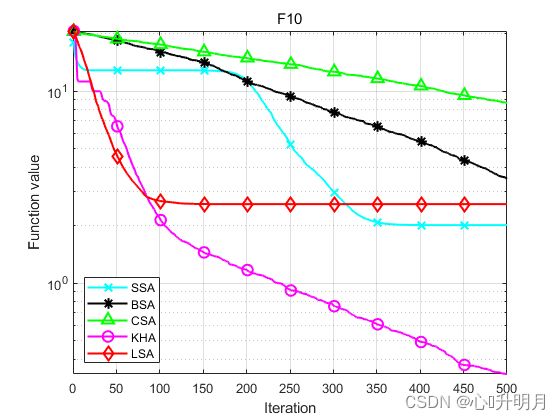
函数:F10
SSA:最差值: 4.0297, 最优值: 3.0024e-05, 平均值: 2.0038, 标准差: 0.96022, 秩和检验: 0.077272
BSA:最差值: 7.3612, 最优值: 1.0224, 平均值: 3.4928, 标准差: 1.3446, 秩和检验: 0.0033386
CSA:最差值: 13.1826, 最优值: 6.2753, 平均值: 8.6649, 标准差: 1.5018, 秩和检验: 3.0199e-11
KHA:最差值: 1.1229, 最优值: 0.23228, 平均值: 0.33559, 标准差: 0.17901, 秩和检验:3.0199e-11
LSA:最差值: 4.5055, 最优值: 1.1551, 平均值: 2.5766, 标准差: 0.83098, 秩和检验: 1
函数:F11
SSA:最差值: 0.051795, 最优值: 2.3635e-05, 平均值: 0.010149, 标准差: 0.011772, 秩和检验: 0.87663
BSA:最差值: 1.2277, 最优值: 0.98283, 平均值: 1.0736, 标准差: 0.057462, 秩和检验: 3.0199e-11
CSA:最差值: 1.2041, 最优值: 1.0805, 平均值: 1.1399, 标准差: 0.033529, 秩和检验: 3.0199e-11
KHA:最差值: 0.93235, 最优值: 0.59206, 平均值: 0.73621, 标准差: 0.079472, 秩和检验:3.0199e-11
LSA:最差值: 0.041738, 最优值: 1.1102e-16, 平均值: 0.012876, 标准差: 0.012825, 秩和检验: 1
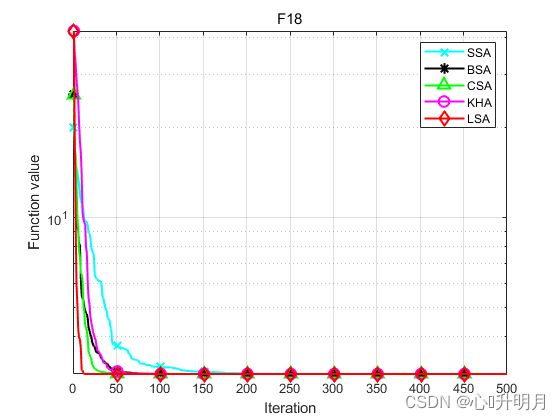
函数:F18
SSA:最差值: 3, 最优值: 3, 平均值: 3, 标准差: 1.1324e-13, 秩和检验: 2.0296e-11
BSA:最差值: 3, 最优值: 3, 平均值: 3, 标准差: 1.3922e-15, 秩和检验: 0.9614
CSA:最差值: 3, 最优值: 3, 平均值: 3, 标准差: 1.6118e-15, 秩和检验: 5.4025e-05
KHA:最差值: 3.0001, 最优值: 3, 平均值: 3, 标准差: 3.0057e-05, 秩和检验:2.0362e-11
LSA:最差值: 3, 最优值: 3, 平均值: 3, 标准差: 1.4473e-15, 秩和检验: 1
函数:F19
SSA:最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 1.407e-13, 秩和检验: 1.2108e-12
BSA:最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.5243e-15, 秩和检验: 5.5934e-05
CSA:最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.4795e-15, 秩和检验: 3.7959e-06
KHA:最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 1.2188e-06, 秩和检验:1.2118e-12
LSA:最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.7101e-15, 秩和检验: NaN
实验结果表明:与其他对比算法相比,LSA方法总体上提供了更好的结果,具有较高的收敛速度。
三、参考文献
[1] Hussain Shareef, Ahmad Asrul Ibrahim, Ammar Hussein Mutlag. Lightning search algorithm[J]. Applied Soft Computing, 2015, 36: 315-333.
[2] 任云, 刘丹. BAS-LSA混合算法在装配序列规划的应用[J]. 组合机床与自动化加工技术, 2021(7): 160-164.