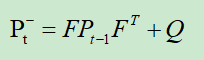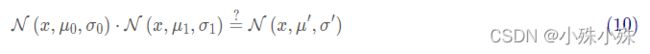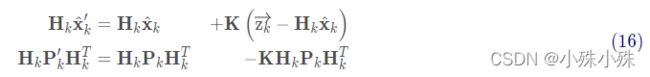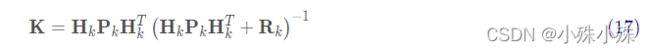【五分钟会，半小时懂】卡尔曼滤波器(Kalman Filter)—目标跟踪（含源码）

目录

效果展示

卡尔曼滤波器的简单介绍

一、公式解释

二、卡尔曼增益的推导

三、第一个例子

四、第二个例子

---

效果展示

卡尔曼滤波-目标跟踪_哔哩哔哩_bilibili

卡尔曼滤波器的简单介绍

        我们可以在任何含有不确定信息的动态系统中的使用卡尔曼滤波，对系统的下一步动作做出有根据的猜测。猜测的依据是预测值和观测值，首先我们认为预测值和观测值都符合高斯分布且包含误差，然后我们预设预测值的误差Q和观测值的误差R，然后计算得到卡尔曼增益，最后利用卡尔曼增益来综合预测值和观测值的结果，得到我们要的最优估计。通俗的说卡尔曼滤波就是将算出来的预测值和观测值综合考虑的过程。

      

一、公式解释

        卡尔曼滤波器的推导过程比较复杂，这里不展开，这篇文章讲推导过程很好，下面5个公式是卡尔曼滤波器的核心，掌握了这5个公式，就基本掌握了卡尔曼滤波器的大致原理，下面只给出卡尔曼增益的推导过程。

几个名词解释：

预测值：根据上一次最优估计计算出来的值。

观测值：很好理解，就是观测到的值，比如观测到的物体的位置、速度。

最优估计：又叫后验状态估计值，滤波器的最终输出，也作为下一次迭代的输入。

卡尔曼滤波器最核心的5个公式：

1. 

状态预测公式，作用是根据上一轮的最优估计，计算本轮的预测值。

其中F称为状态转移矩阵，表示我们如何从上一状态推测出当前状态；B表示控制矩阵，表示控制量u对当前状态的影响；u表示控制量，比如加速度；x头上之所以加一个^表示它是一个估计值，而不是真实值，而-上标表示这并非最佳估计。

2.

噪声协方差公式，表示不确定性在各个时刻之间的传递关系，作用是计算本轮预测值的系统噪声协方差矩阵。

F表示状态转移矩阵，P为系统噪声协方差矩阵（即每次的预测值和上一次最优估计误差的协方差矩阵），Q为表示误差的矩阵

3.

计算K卡尔曼系数，又叫卡尔曼增益。

H表示观测矩阵，R表示观测噪声的协方差矩阵

卡尔曼系数的作用主要有两个方面：

    第一是权衡预测状态协方差矩阵P和观察量协方差矩阵R的大小，来决定我们是相信预测模型多一点还是观察模型多一点。如果相信预测模型多一点，这个残差的权重就会小一点，如果相信观察模型多一点，权重就会大一点。

    第二就是把残差的表现形式从观察域转换到状态域，在我们这个例子中，观察值z表示的是小车的位置，只是一个一维向量，而状态向量是一个二维向量，它们所使用的单位和描述的特征都是不同的。而卡尔曼系数就是要实现这样将一维的观测向量转换为二维的状态向量的残差，在本例中我们只观测了小车的位置，而在K中已经包含了协方差矩阵P的信息，所以就利用了位置和速度这两个维度的相关性，从位置的信息中推测出了速度的信息，从而让我们可以对状态量x的两个维度同时进行修正。

4. 

最优估计公式，作用是利用观测值和预测值的残差对当前预测值进行调整，用的就是加权求和的方式。

z是观测值，K是卡尔曼系数。

5. 

更新过程噪声协方差矩阵，下一次迭代中2式使用。

二、卡尔曼增益的推导

        我收集网上大佬的文章，发现这篇文章通俗易懂，摘录其中卡尔曼增益的推导部分。

先以一维高斯分布来分析比较简单点，具有方差和均值μ的高斯曲线可以用下式表示：

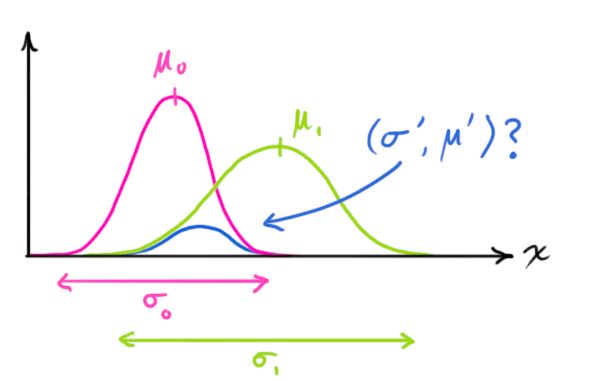
   两个高斯分布相乘会得到一个新的高斯分布，如下图，紫色的分布乘以绿色的分布得到蓝色的分布。

 将式（9）代入到式（10）中（注意重新归一化，使总概率为1）可以得到：

 将式（11）中的两个式子相同的部分用 k表示：

 

         根据（12）可以看出，K就是第一个分布的方差所占比例，即预测值的方差所占比例，K越大则最优估计越倾向于相信观测值。下面进一步将式（12）和（13）写成矩阵的形式，如果Σ表示高斯分布的协方差，μ表示每个维度的均值，则：

        矩阵K称为卡尔曼增益 ，接下来整合上述公式：

        我们有两个高斯分布，预测部分(μ0, Σ0)和测量部分(μ1, Σ1)，将他们放到式(15)中算出它们之间的重叠部分：

         由式（14）可得卡尔曼增益为：

将式（16）和式（17）的两边同时左乘矩阵的逆（注意K里面包含了Hk​）将其约掉，再将式（16）的第二个等式两边同时右乘矩阵HkT​的逆得到以下等式： 

 

         上式给出了完整的更新步骤方程。x^k​就是新的最优估计，我们可以将它和Pk​放到下一个预测和更新方程中不断迭代。

三、第一个例子

        下面是一个简单模拟预测小车位置和速度的一段程序，观测的值是一段从0到99，速度为1的匀速行驶路径，加入的噪声是均值为0，方差为1的高斯噪声。

import numpy as np
import matplotlib.pyplot as plt

# 创建一个0-99的一维矩阵
z = [i for i in range(100)]
z_watch = np.mat(z)

# 创建一个方差为1的高斯噪声，精确到小数点后两位
noise = np.round(np.random.normal(0, 1, 100), 2)
noise_mat = np.mat(noise)

# 将z的观测值和噪声相加
z_mat = z_watch + noise_mat

# 定义x的初始状态，即位置和速度
x_mat = np.mat([[0, ], [0, ]])
# 定义初始状态协方差矩阵,这个矩阵在迭代中会被更新
p_mat = np.mat([[0, 0], [0, 0]])
# 定义状态转移矩阵
# 第一行算位置，1：老的位置 1：delta_t=1 每秒钟采一次样
# 第二行算速度，0：速度跟老的位置没关系 1：跟上一次最优估计的速度一样
f_mat = np.mat([[1, 1], [0, 1]])
# 定义状态转移协方差矩阵，这里我们把协方差设置的很小，因为觉得状态转移矩阵准确度高
q_mat = np.mat([[0.0001, 0], [0, 0.0001]])
# 定义观测矩阵，如果状态有两项，观测只有一项，那么观测矩阵H是一个[1 0]，如果观测的有两项这两项那么观测的矩阵是[1 1]；
h_mat = np.mat([1, 0])
# 定义观测噪声协方差
r_mat = np.mat([1])

for i in range(100):
    x_predict = f_mat * x_mat
    p_predict = f_mat * p_mat * f_mat.T + q_mat
    kalman = p_predict * h_mat.T / (h_mat * p_predict * h_mat.T + r_mat)
    x_mat = x_predict + kalman * (z_mat[0, i] - h_mat * x_predict)
    p_mat = (np.eye(2) - kalman * h_mat) * p_predict

    plt.plot(x_mat[0, 0], x_mat[1, 0], 'ro', markersize=1)

plt.show()

运行结果：

        横坐标表示离初始位置的距离p，纵坐标表示在该位置的速度v。可以发现，开始时预测值和实际值有较大出入，在经过一段很短的时间后，速度预测值与实际值1基本就很接近了！

四、第二个例子

下面使用opencv实现目标跟踪，跟踪绿色小球，绿线是观测值，红线是最佳估计。

运行结果：卡尔曼滤波-目标跟踪_哔哩哔哩_bilibili

import cv2
import numpy as np
# hsv阈值，便于进行轮廓判断及轨迹绘制，需要根据运动目标的颜色自己进行调整
min_hsv_bound = (35, 100, 100)
max_hsv_bound = (77, 255, 255)
#状态向量
stateSize = 6
#观测向量
measSize = 4
coutrSize = 0
kf = cv2.KalmanFilter(stateSize,measSize,coutrSize)
state = np.zeros(stateSize, np.float32)#[x,y,v_x,v_y,w,h],簇心位置，速度，高宽
meas = np.zeros(measSize, np.float32)#[z_x,z_y,z_w,z_h]
procNoise = np.zeros(stateSize, np.float32)

#状态转移矩阵
print('kf.transitionMatrixa', kf.transitionMatrix)
cv2.setIdentity(kf.transitionMatrix)#生成单位矩阵
print('kf.transitionMatrixb', kf.transitionMatrix)
# [1 0 dT 0  0 0]
# [0 1 0  dT 0 0]
# [0 0 1  0  0 0]
# [0 0 0  1  0 0]
# [0 0 0  0  1 0]
# [0 0 0  0  0 1]
#观测矩阵
# [1 0 0 0 0 0]
# [0 1 0 0 0 0]
# [0 0 0 0 1 0]
# [0 0 0 0 0 1]
kf.measurementMatrix = np.zeros((measSize,stateSize),np.float32)
kf.measurementMatrix[0,0]=1.0
kf.measurementMatrix[1,1]=1.0
kf.measurementMatrix[2,4]=1.0
kf.measurementMatrix[3,5]=1.0

#预测噪声
# [Ex 0 0 0 0 0]
# [0 Ey 0 0 0 0]
# [0 0 Ev_x 0 0 0]
# [0 0 0 Ev_y 0 0]
# [0 0 0 0 Ew 0]
# [0 0 0 0 0 Eh]
cv2.setIdentity(kf.processNoiseCov)
kf.processNoiseCov[0,0] = 1e-2
kf.processNoiseCov[1,1] = 1e-2
kf.processNoiseCov[2,2] = 5.0
kf.processNoiseCov[3,3] = 5.0
kf.processNoiseCov[4,4] = 1e-2
kf.processNoiseCov[5,5] = 1e-2

#测量噪声
cv2.setIdentity(kf.measurementNoiseCov)
# for i in range(len(kf.measurementNoiseCov)):
#     kf.measurementNoiseCov[i,i] = 1e-1

video_cap = cv2.VideoCapture('./video/green_ball.mp4')
# 视频输出
fps = video_cap.get(cv2.CAP_PROP_FPS) #获得视频帧率，即每秒多少帧
size = (int(video_cap.get(cv2.CAP_PROP_FRAME_WIDTH)),int(video_cap.get(cv2.CAP_PROP_FRAME_HEIGHT)))
videoWriter = cv2.VideoWriter('./video/new_green.mp4' ,cv2.VideoWriter_fourcc('m', 'p', '4', 'v'), fps, size)
ticks = 0
i=0
found = False
notFoundCount = 0
prePointCen = [] #存储小球中心点位置
meaPointCen = []
while(True):
    ret, frame = video_cap.read()
    if ret is False:
        break
    cv2.imshow('frame',frame)
    cv2.waitKey(1)
    precTick = ticks
    ticks = float(cv2.getTickCount())
    res = frame.copy()
    # dT = float(1/fps)
    dT = float((ticks - precTick)/cv2.getTickFrequency())
    if(found):
        #预测得到的小球位置
        kf.transitionMatrix[0,2] = dT
        kf.transitionMatrix[1,3] = dT
        print('kf.transitionMatrix1', kf.transitionMatrix)

        state = kf.predict()
        print('kf.transitionMatrix2:', kf.transitionMatrix)
        width = state[4]
        height = state[5]
        x_left = state[0] - width/2 #左上角横坐标
        y_left = state[1] - height/2  #左上角纵坐标
        x_right = state[0] + width/2
        y_right = state[1] + height/2
        print('kf.transitionMatrix3:', kf.transitionMatrix)

        center_x = state[0]
        center_y = state[1]
        prePointCen.append((int(center_x),int(center_y)))
        cv2.circle(res, (int(center_x),int(center_y)),2,(255,0,0),-1)
        cv2.rectangle(res,(x_left,y_left),(x_right,y_right),(255,0,0),2)
        print('kf.transitionMatrix4:', kf.transitionMatrix)

    #根据颜色二值化得到的小球位置
    frame = cv2.GaussianBlur(frame, (5,5), 3.0, 3.0)
    frame = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
    rangeRes = cv2.inRange(frame, min_hsv_bound,max_hsv_bound)
    kernel = np.ones((3, 3), np.uint8)
    # 腐蚀膨胀
    rangeRes = cv2.erode(rangeRes, kernel, iterations=2)
    rangeRes = cv2.dilate(rangeRes, kernel, iterations=2)
    # cv2.imshow("Threshold", rangeRes)
    cv2.waitKey(1)
    contours = cv2.findContours(rangeRes.copy(),cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_NONE)[-2]
    #检测轮廓，只检测最外围轮廓，保存物体边界上所有连续的轮廓点到contours向量内
    balls = []
    ballsBox = []
    for i in range(len(contours)):
        x, y, w, h = cv2.boundingRect(np.array(contours[i]))

        ratio = float(w/h)
        if(ratio > 1.0):
            ratio = 1.0 / ratio
        if(ratio > 0.75 and w*h>=400):
            balls.append(contours[i])
            ballsBox.append([x, y, w, h])

    print( "Balls found:", len(ballsBox))
    print("\n")

    for i in range(len(balls)):
        # 绘制小球轮廓
        cv2.drawContours(res, balls, i, (20,150,20),1)
        cv2.rectangle(res,(ballsBox[i][0],ballsBox[i][1]),(ballsBox[i][0]+ballsBox[i][2],ballsBox[i][1]+ballsBox[i][3]),(0,255,0),2) #二值化得到小球边界

        center_x = ballsBox[i][0] + ballsBox[i][2] / 2
        center_y = ballsBox[i][1] + ballsBox[i][3] / 2

        meaPointCen.append((int(center_x),int(center_y)))
        cv2.circle(res,(int(center_x),int(center_y)), 2, (20,150,20) ,-1)

        name = "(" + str(center_x) + "," + str(center_y) + ")"
        cv2.putText(res, name, (int(center_x) + 3, int(center_y) - 3), cv2.FONT_HERSHEY_COMPLEX, 0.5, (20,150,20), 2)
    n = len(prePointCen)
    for i in range(1, n):
        print(i)
        if prePointCen[i-1] is None or prePointCen[i] is None:
            continue
         #  注释掉的这块是为了绘制能够随时间先后慢慢消失的追踪轨迹，但是有一些小错误
        # 计算所画小线段的粗细
        # thickness = int(np.sqrt(64 / float(n - i + 1))*2.5)
        # print(thickness)
        # 画出小线段
        # cv2.line(res, prePointCen[i-1], prePointCen[i], (0, 0, 255), 1)
        cv2.line(res, prePointCen[i-1], prePointCen[i], (0,0,255), 1, 4)
    n = len(meaPointCen)
    for i in range(1, n):
        print(i)
        if meaPointCen[i - 1] is None or meaPointCen[i] is None:
            continue
        #  注释掉的这块是为了绘制能够随时间先后慢慢消失的追踪轨迹，但是有一些小错误
        # 计算所画小线段的粗细
        # thickness = int(np.sqrt(64 / float(n - i + 1))*2.5)
        # print(thickness)
        # 画出小线段
        cv2.line(res, meaPointCen[i - 1], meaPointCen[i], (0, 255, 0), 1, 4)
    if(len(balls) == 0):
        notFoundCount += 1
        print("notFoundCount",notFoundCount)
        print("\n")

        if notFoundCount >= 100:
            found = False

    else:
        #测量得到的物体位置
        notFoundCount = 0
        meas[0] = ballsBox[0][0] + ballsBox[0][2] / 2
        meas[1] = ballsBox[0][1] + ballsBox[0][3] / 2
        meas[2] = float(ballsBox[0][2])
        meas[3] = float(ballsBox[0][3])
        #第一次检测
        if not found:
            for i in range(len(kf.errorCovPre)):
                kf.errorCovPre[i,i] = 1
            state[0] = meas[0]
            state[1] = meas[1]
            state[2] = 0
            state[3] = 0
            state[4] = meas[2]
            state[5] = meas[3]

            kf.statePost = state
            found = True

        else:
            kf.correct(meas) #Kalman修正

            print('rr',res.shape)
            print("Measure matrix:", meas)
            cv2.imshow("Tracking", res)

            cv2.waitKey(1)
    videoWriter.write(res)