树的基本概念和二叉树的遍历

树和二叉树的遍历

一、树的定义与存储
1、
树的定义

在计算机科学中，树是一种非线性结构，存储的是具有“一对多”关系的数据元素的集合；（是不是像一个家族关系表）

2、
树的基本术语

3、
树形结构

用链表表示树的结点

二、二叉树的定义和性质

N个节点的有限集，每个节点至多有两颗子树，二叉树的子树有左右之分，不能任意颠倒。

二叉树有五种基本形态：

特殊二叉树：

性质：

l 在二叉树的第i层上至多有2i-1个结点（i>=1）.

l
深度为k的二叉树至多有2k-1个结点

l
对任意一颗二叉树T，如果其终端结点为N0，度为2的结点数为N2，则N0=N2+1；

l
具有N个结点的完全二叉树的深度为[log2N]+1；

三、二叉树的存储结构

完全二叉树可以用数组表示（满二叉树是一种特殊的完全二叉树）

用数组存的特点：

（1）、非根节点i的父亲结点的序号为[i/2];

（2）、结点i的左孩子序号为2*i；

（3）、结点i的右孩子序号为2*i+1；

二叉链表：

四、二叉树的遍历

本质：按某种路径访问树中的每个节点，使每个节点均被访问一次，且仅被访问一次；

二叉树有三种常见遍历：先序遍历（有时候称为前序遍历）、中序遍历、后序遍历；

1、
先序遍历（根左右）

//二叉树的先序遍历

void PreTree(bTree T) {
    if (T) {
        printf("%c ", T->data);
        PreTree(T->Lchild);
        PreTree(T->Rchild);
    }
}

2、
中序遍历（左根右）

//二叉树的中序遍历

void InTree(bTree T) {
    if (T) {
        InTree(T->Lchild);
        printf("%c ", T->data);
        InTree(T->Rchild);
    }
}

3、
后序遍历（左右根）
//二叉树的后序遍历

void PostTree(bTree T) {
    if (T) {
        PostTree(T->Lchild);
        PostTree(T->Rchild);
        printf("%c ", T->data);
    }
}

三种常见遍历一定要记住，（其实也非常容易记，注意根的位置就行了）

4、
非递归算法（也就是循环，用到栈）（*）

//非递归遍历

void StackTree(bTree T) {
    stack s;//定义一个结构体类型的栈
    if (T == NULL) {
        printf("the tree is null.\n");
        return ;
    }
    while (T || !s.empty()) {//中序遍历为例,树不空或栈不空时循环
        if (T) {//判断树是否为空
            s.push(T);//根指针进栈，遍历左子树
            T = T->Lchild;
        }
        else {//根指针退栈，访问根节点，遍历右子树
            T = s.top();
            printf("%c ", T->data);
            s.pop();
            T = T->Rchild;
        }
    }
}

5、层次遍历（*）

按照从上到下、从左至右的循序访问（用队列实现）
//层次遍历

void QueueTree(bTree T) {
    queue Q;//定义BTree类型的队列
    if (!T) return;//若是空树直接返回
    while (!Q.empty())//队列不为空则清除最前面的元素，直到队列为空
        Q.pop();
    Q.push(T);//根节点入队
    while (!Q.empty()) {//队列不为空则继续循环
        T = Q.front();//读取队头元素
        printf("%c ", T->data);
        Q.pop();//队头出队
        if (T->Lchild)Q.push(T->Lchild);//左孩子入队尾
        if (T->Rchild)Q.push(T->Rchild);//右孩子入队尾
    }
}

五、树和森林

简单来讲，森林就是树的集合。

数、森林、二叉树的转换：

https://jingyan.baidu.com/article/19020a0a743851529d28421a.html

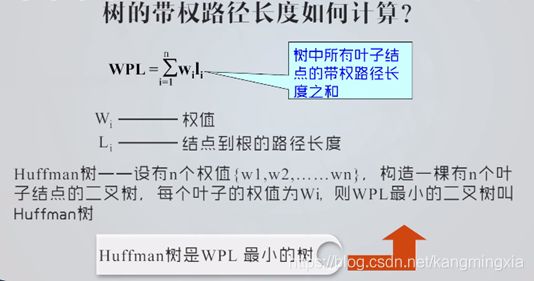
六、哈夫曼树与哈夫曼编码（*）

Huffman树（最优二叉树）：带权路径长度最小的树

在这里插入图片描述

哈夫曼树的构造：

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：

(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；

(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

(3)从森林中删除选取的两棵树，并将新树加入森林；

(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

哈夫曼编码：左分支0，右分支1（主要用于网络报文传输）