【练习】04:栈相关操作
Stack栈
目录
- Stack栈
-
-
-
- 1.顺序栈操作:
- 2.顺序栈扩容:
- 3.LC20:ValidParathese
-
- (1)方法1:简化思维:
- (2)方法2:stack栈解决:
- 4.链栈基本操作:
- 5.栈和队列的应用:
-
-
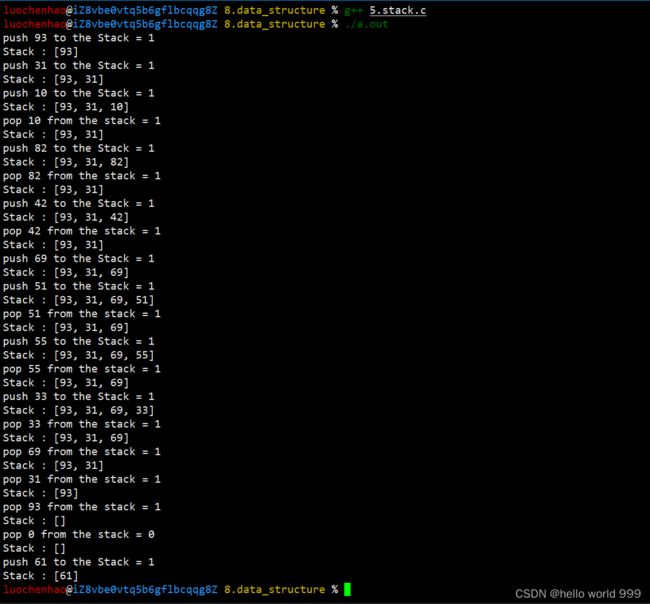
1.顺序栈操作:
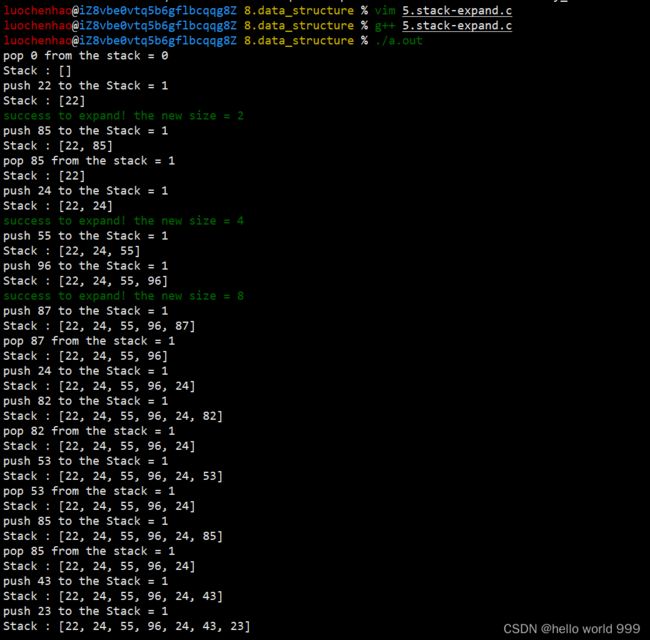
#include2.顺序栈扩容:
关键代码:
//SqStack扩容操作
int expand(SqStack *s) {
int expand_size = s->stacksize;
int *p;
//顺序栈的循环扩容
while (expand_size) {
p = (int *)realloc(s->base, sizeof(int) * (s->stacksize + expand_size));
if (p != NULL) break;//realloc扩容成功
expand_size >>= 1;//realloc扩容失败则将扩容容量extend缩小,再次尝试扩容
}
if (p == NULL) return 0;
s->stacksize += expand_size;
s->base = p;
return 1;
}
//5.入栈操作
int Push(SqStack *s, int val) {
if (s == NULL) return 0;
if (s->top == s->stacksize - 1) {
if (!expand(s)) {
printf(RED("fail to expand!\n"));
return 0;
}
printf(GREEN("success to expand! the new size = %d\n"), s->stacksize);
}
s->top++;//注意:这里栈顶指针指向的是栈顶元素故需要先++再赋值
s->base[s->top] = val;
return 1;
}
完整代码:
#include3.LC20:ValidParathese
Given a string s containing just the characters (, ), {, }, [ and ], determine if the input string is valid.
An input string is valid if:
Open brackets must be closed by the same type of brackets.
Open brackets must be closed in the correct order.
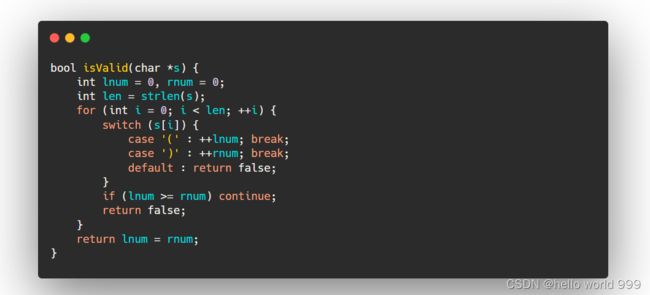
(1)方法1:简化思维:
可以将问题先简化为1种括号的匹配问题(判断左括号、右括号的数量是否相等),再扩展括号匹配的种类:
+1可以等价为进入,-1可以等价为出去- 一对
()可以等价为一个完整的事件 (())可以看做事件与事件之间的完全包含关系
1种括号的匹配问题:
多种括号的匹配问题:
#include注意:该程序虽然可以判断成功,但是执行的时间复杂度太高导致超时。
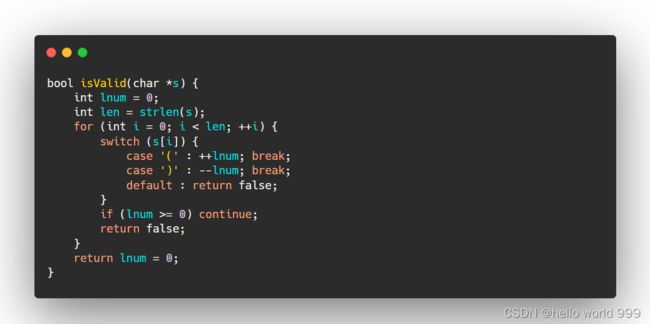
(2)方法2:stack栈解决:
#include 4.链栈基本操作:
#include