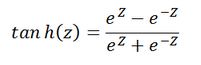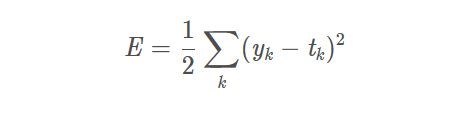BackPropagation神经网络的学习与浅析

前言

人工智能学习相关博客:

    Pytorch识别手写体数字的简单实现

数据可视化相关博客：

    Pyecharts的实例使用

     去年大二上学期的时候，突然想尝试一下神经网络与深度学习的学习。毕竟博主是想以后做计算机视觉的，于是找我的导师闻了一下相关的学习方法，于是导师给了我一个预测判断牧场动物行为的项目。说实话，一开始心里还是挺没谱的，毕竟我还啥都不会啊ToT。不过人都不是从0到1的质变提升吗？所以我自己就买了一堆的书。在这里我是比较推荐

1. ‘中国水利水电出版社’刘瑜先生的《Python编程》
2. ‘中国水利水电出版社’蒋子阳先生的《TensorFlow深度学习算法原理与编程实战》
3. ‘人民邮电出版社’斋藤康毅先生的《深度学习入门》
4. ‘人民邮电出版社’塔里克·拉希德先生的《Python神经网络编程》
5. ‘人民邮电出版社’IAN GOODFELLOW,YOSHUA BENGIO,AARON COURVILLE三位联合著写的《DEEP LEARNING》

     关于视频课程的话，我推荐去B站的莫烦Python，吴恩达先生的视频，以及3Blue1Brown等等。

壹.关于各种库的安装

     其实在我很多博客里面都有说过，如果还是不会安装库的同学请自行BaiDu或者阅读我之前的python博客。

import numpy as np#numpy做矩阵运算十分方便
import math#math函数用来设置一些激活函数
import random#需要随机数来做初始权重
import string
import matplotlib as mpl#如果你需要作图就用上
import matplotlib.pyplot as plt
import sys#需要保存最后的合理权重
import xlrd#因为我的数据集是从excel里面读出来的
from sklearn import preprocessing#需要对数据集做高斯分布或归一化的可以用这个

读取数据

     我这里是用的来自牧场方面给的Excel里面的各项数据集，如果是用MNIST或者其他来源的数据集的朋友可以跳过该步骤。差不多是一个三维的数据，我每次从两种行为里面取500组数据放入数组，并且给他们贴上0或1的标签【【【954】，【4652】，【-456】】【1】】差不多就是这种，前面是三维列表，后面是贴上的标签。

def read_excel():
    # 打开Excel
    workbook = xlrd.open_workbook('all.xls')
    # 进入sheet
    eating = workbook.sheet_by_index(0)
    sleeping=workbook.sheet_by_index(1)
    # 获取行数和列叔
    Srows_num=sleeping.nrows
    Scols_num=sleeping.ncols
    ListSleep=[]
    
    Erows_num = eating.nrows
    Ecols_num = eating.ncols
    ListEat=[]
    ListEatT=[]
    ListSleepT=[]
    ListT=[]
    i = 1
    while i <= 500:
        if Erows_num > 10 or Srows_num>10:
            # 生成随机数
            random_numE = random.randint(1, Erows_num - 1)
            E_X = eating.row(random_numE)[1].value
            E_Y = eating.row(random_numE)[3].value
            E_Z = eating.row(random_numE)[5].value
            ListEat.append([[int(E_X),int(E_Y),int(E_Z)],[1]])
            random_numS = random.randint(1, Srows_num - 1)
            S_X = sleeping.row(random_numS)[1].value
            S_Y = sleeping.row(random_numS)[3].value
            S_Z = sleeping.row(random_numS)[5].value
            ListSleep.append([[int(S_X),int(S_Y),int(S_Z)],[0]])
            i = i + 1
        else:
            print("数据不足，请添加")
            break
    List=ListEat+ListSleep
    
    print(List)
read_excel()

贰.激活函数

      这里是最重要的一步，一个好的适用的激活函数决定你这个网络的质量。

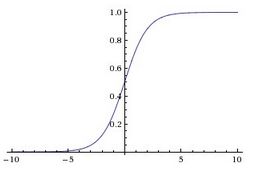
      1、sigmoid函数

       sigmoid函数曲线如下:

         sigmoid激活函数，符合实际，当输入值很小时，输出接近于0；当输入值很大时，输出值接近于1。但sigmoid激活函数有较  大的缺点，是主要有两点：

（1）容易引起梯度消失。当输入值很小或很大时，梯度趋向于0，相当于函数曲线左右两端函数导数趋向于0。

（2）非零中心化，会影响梯度下降的动态性。

def sigmoid(x):
    '''
    定义sigmoid函数
    '''
    return 1.0/(1.0+np.exp(-x))
def derived_sigmoid(x):
    '''
    定义sigmoid导函数
    '''
    return sigmoid(x)*(1-sigmoid(x))

     2、tanh函数

     tanh函数曲线如下：

     与sigmoid相比，输出至的范围变成了0中心化[-1, 1]。但梯度消失现象依然存在。

def tanh(x):
    '''
    定义tanh函数
    '''
    return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
def derived_tanh(x):
    '''
    定义tanh导函数
    '''
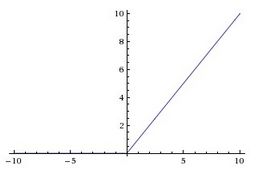
    return 1-tanh(x)*tanh(x)

     3、Relu函数

     Relu修正线性单元是有许多优点，是目前神经网络中使用最多的激活函数。

     函数曲线如下：

优点：（1）不会出现梯度消失，收敛速度快；

          （2）前向计算量小，只需要计算max(0, x)，不像sigmoid中有指数计算；

          （3）反向传播计算快，导数计算简单，无需指数、出发计算；

          （4）有些神经元的值为0，使网络具有saprse性质，可减小过拟合。

缺点：（1）比较脆弱，在训练时容易“死亡”，反向传播中如果一个参数为0，后面的参数就会不更新。使用合适的学习率会减弱这种情况。

def relu(x):
    '''relu函数'''
    return np.where(x<0,0,x)
 
def derivedrelu(x):
    '''relu的导函数'''
    return np.where(x<0,0,1)

     4、Leak Relu函数

     Leak Relu是对Relu缺点的改进，当输入值小于0时，输出值为αx，其中α是一个很小的常数。这样在反向传播中就不容易出现“die”的情况。

def leakyrelu(x,a=0.01):
    '''
    定义leakyrelu函数
    leakyrelu激活函数是relu的衍变版本，主要就是为了解决relu输出为0的问题
    '''
    return np.where(x<0,a*x,x)
 
def derived_leakyrelu(x,a=0.01):
    '''
    定义leakyrelu导函数
    '''
    return np.where(x<0,a,1)

     4、elu函数

 # 定义elu函数elu和relu的区别在负区间，relu输出为0，而elu输出会逐渐接近-α，更具鲁棒性。
def elu(x,a=0.01):
 #elu激活函数另一优点是它将输出值的均值控制为0（这一点确实和BN很像，BN将分布控制到均值为0，标准差为1）
    return np.where(x<0,a*(np.exp(x)-1),x)
 
def derived_elu(x,a=0.01):
    '''
    定义elu导函数
    '''
    return np.where(x<0,a*np.exp(x),1)

 除此之外还有很多派生的激活函数，请各位自己发掘了。

叁.数据的归一化处理

  输入输出数据的预处理：尺度变换。尺度变化也称为归一化或者标准化，是指变换处理将网络的输入、输出数据限制在[0,1]或者[-1,1]等区间内。进行变换的原因有三点：

 1）.网络的各个输入数据常常具有不同的物理意义和不同的量纲。尺度变换使所有分量都在一个区间内变化，从而使网络训练一开始就给各输入分量以同等重要的地位；

 2）.BP神经网络神经元均采用sigmoid函数，变换后可防止因净输入的绝对值过大而使神经元输出饱和，继而使权值调整进入误差曲面的平坦区；

 3）.sigmoid函数输出在区间[0,1]或者是tanh函数[-1,1]内，如果不对期望输出数据进行变换处理，势必使数值大的分量绝对误差大，数值小的分量绝对误差小，总之数据最好要归一化。

2、（0,1)标准化：

  这是最简单也是最容易想到的方法，通过遍历feature vector里的每一个数据，将Max和Min的记录下来，并通过Max-Min作为基数（即Min=0，Max=1）进行数据的归一化处理：

 　　　　　　　　　　　　　　　　　　　　

Python实现：

def MaxMin(x,Max,Min):
    x = (x - Min) / (Max - Min);
    return x

2、Z-score标准化：

这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1，这里的关键在于复合标准正态分布：

 

　　　　　　　　　　　　　　　　　　　　 

Python实现：

def Z_Score(x,mu,sigma):
    x = (x - mu) / sigma;
    return x

3、均值归一化

两种方式，以max为分母的归一化方法和以max-min为分母的归一化方法

 

def average():
    # 均值
    average = float(sum(data))/len(data)
 
    # 均值归一化方法
    data2_1 = [(x - average )/max(data) for x in data]
    data2_2 = [(x - average )/(max(data) - min(data)) for x in data]

肆.误差函数/损失函数

     一、均方误差Mean Squared Error

yk​是NN的输出
tk​是标签，只有正确解的标签为1，其他均为0.   k是数据维数
所以，均方误差计算NN的输出和正确标签数据的各个元素的差值的平方，再求总和。

def get_standard_deviation(records):
    """
    标准差 == 均方差 反映一个数据集的离散程度
    """
    variance = get_variance(records)
    return math.sqrt(variance)

     二、平均值average

def get_average(records):
    """
    平均值
    """
    return sum(records) / len(records)

    三、交叉熵误差Cross Entropy Error

单个训练数据的交叉熵误差只计算正确解标签的输出的自然对数。

yk​是NN的输出tk​标签，只有正确解的标签为1，其他均为0，k是数据维数

所以，当NN输出的正确解的概率y为1时，交叉熵损失为0；随着正确解的概率y向0减小，交叉熵损失减小（向负值减小，实际上损失值是在增大）

def cross_entropy(a, y):
    return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a)))
 
# tensorflow version
loss = tf.reduce_mean(-tf.reduce_sum(y_*tf.log(y), reduction_indices=[1]))
 
# numpy version
loss = np.mean(-np.sum(y_*np.log(y), axis=1))

 

伍.构建神经网络

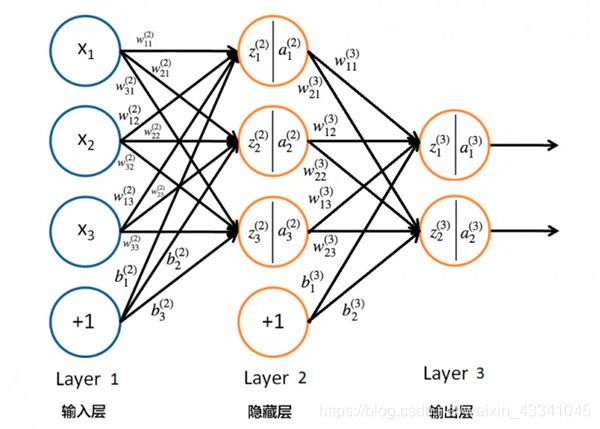
   这上面的图只是一个示例，我最后的输出只有一个输出点，通过判断接近0或者1来判断行为的，多分类问题建议最后用softmax。这里的初始权值我有必要先说一下，最好设置为2的倍数，特别是要GPU加速的同学。
 

# 构造三层BP网络架构

class BPNN:
    def __init__(self, num_in, num_hidden, num_out):
        # 输入层，隐藏层，输出层的节点数
        self.num_in = num_in + 1  # 增加一个偏置结点
        self.num_hidden = num_hidden + 1  # 增加一个偏置结点
        self.num_out = num_out
        # 激活神经网络的所有节点（向量）
        self.active_in = [1.0] * self.num_in
        self.active_hidden = [1.0] * self.num_hidden
        self.active_out = [1.0] * self.num_out
        # 创建权重矩阵
        self.wight_in = makematrix(self.num_in, self.num_hidden)
        self.wight_out = makematrix(self.num_hidden, self.num_out)
        # 对权值矩阵赋初值

        for i in range(self.num_in):
            for j in range(self.num_hidden):
                self.wight_in[i][j] = random_number(-2.4, 2.4)
        for i in range(self.num_hidden):
            for j in range(self.num_out):
                self.wight_out[i][j] = random_number(-0.2, 0.2)
        # 最后建立动量因子（矩阵）
        self.ci = makematrix(self.num_in, self.num_hidden)
        self.co = makematrix(self.num_hidden, self.num_out)

     正向传播，这里我用了sigmoid作为初始数据集的归一化，因为我这里的数据最大和最小差的太多1000和3这种差距，像这种数据之间有太大的差异一定要归一化。tanh作为隐含层的激活函数，把隐含层的数据都统一在[-1,1]之间。最后用sigmoid输出判断这个数据靠近1还是靠近0。

   def update(self, inputs):
        print(len(inputs))
        if len(inputs) != self.num_in - 1:
            raise ValueError('输入层节点数有误')
            # 数据输入输入层
        for i in range(self.num_in - 1):
            self.active_in[i] = sigmoid(inputs[i])  #在输入层进行数据处理归一化

            self.active_in[i] = inputs[i]  # active_in[]是输入数据的矩阵
            # 数据在隐藏层的处理
        for i in range(self.num_hidden - 1):
            sum = 0.0
            for j in range(self.num_in):
                sum = sum + self.active_in[i] * self.wight_in[j][i]

            self.active_hidden[i] = tanh(sum)  # active_hidden[]是处理完输入数据之后存储，作为输出层的输入数据

            # 数据在输出层的处理
        for i in range(self.num_out):
            sum = 0.0
            print(self.wight_out)
            for j in range(self.num_hidden):

                sum = sum + self.active_hidden[j] * self.wight_out[j][i]
            self.active_out[i] = sigmoid(sum)  # 与上同理
        return self.active_out[:]

     反向传播

# 误差反向传播
    def errorback(self, targets, lr, m):  # lr是学习率， m是动量因子
        if len(targets) != self.num_out:
            raise ValueError('与输出层节点数不符！')
            # 首先计算输出层的误差
        out_deltas = [0.0] * self.num_out
        for i in range(self.num_out):
            error = targets[i] - self.active_out[i]
            out_deltas[i] = derived_sigmoid(self.active_out[i]) * error

            # 然后计算隐藏层误差
        hidden_deltas = [0.0] * self.num_hidden
        for i in range(self.num_hidden):
            error = 0.0
            for j in range(self.num_out):
                error = error + out_deltas[j] * self.wight_out[i][j]
            hidden_deltas[i] = derived_tanh(self.active_hidden[i]) * error

            # 首先更新输出层权值
        for i in range(self.num_hidden):
            for j in range(self.num_out):
                change = out_deltas[j] * self.active_hidden[i]
                self.wight_out[i][j] = self.wight_out[i][j] + lr * change + m * self.co[i][j]
                self.co[i][j] = change
            # 然后更新输入层权值
        for i in range(self.num_in):
            for j in range(self.num_hidden):
                change = hidden_deltas[j] * self.active_in[i]
                self.wight_in[i][j] = self.wight_in[i][j] + lr * change + m * self.ci[i][j]
                self.ci[i][j] = change
            # 计算总误差
        error = 0.0
        for i in range(len(targets)):
            error = error + 0.5 * (targets[i] - self.active_out[i]) ** 2

        return error

训练时j[0]为输入的三维列表，j[1]为每个列表的标签，lr为学习率，因为随着梯度的下降，学习率最好也随着缩小，就像一个人学习，一开始要学得多，最后要学得精。

 

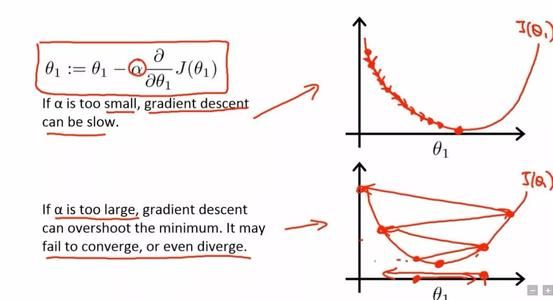
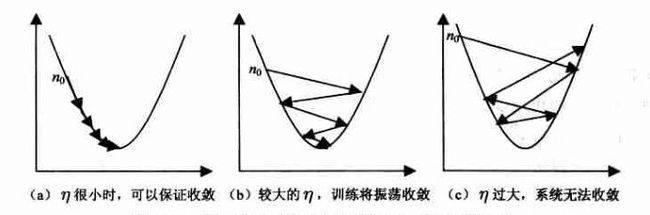
BP算法的改进可以使用动量法m
动量法是在标准BP算法的权值更新阶段引入动量因子α（0<α<1）,使权值修正具有一定惯性，也就是说误差能基本不变化其返回的信号对权值调整很小但是总误差能又大于训练结果设定的总误差能条件。这个时候加入一个动量因子有助于其反馈的误差信号使神经元的权值重新振荡起来。在原有的权值调整公式中，加入了动量因子以及上一次的权值改变量。加入的动量项表示本次权值的更新方向和幅度，不但与本次计算所得的梯度有关，还与上一次更新的方向和幅度有关。动量项反映了以前积累的调整经验，对于t时刻的调整起到了阻尼作用。当误差曲面出现骤然起伏时，可减小震荡趋势，提高训练速度。

 

  def train(self, pattern, itera=200000, lr=0.1, a=0.5):
        for i in range(itera):
            error = 0.0
            for j in pattern:
                input = j[0]
                targ = j[1]
                self.update(input)
                error = error + self.errorback(targ, lr, m)
            if i % 200 == 0:
                lr*=0.99
                print('误差 %-.5f' % error)

 记录下最后的权重保存在txt文档中

    def weights(self):
        f = open("getwights.txt", "w")
        weightin = []
        weightout = []
        print("输入层权重")
        for i in range(self.num_in):
            print(self.wight_in[i])
            weightin.append(self.wight_in[i])

        print("输入矩阵", weightin)
        print("输出层权重")
        for i in range(self.num_hidden):
            print(self.wight_out[i])
            weightout.append(self.wight_out[i])

        print("输出矩阵", weightout)
        f.write(str(weightin))
        f.write("\n")
        f.write(str(weightout))
        f.close()

然后创建神经网络，如果你不是3X3X1类型，也可以自己修改，然后在class里面也修改一下节点个数一样可以使用

def BP():
# 创建神经网络，3个输入节点，3  个隐藏层节点，1个输出层节点
    n = BPNN(3, 3, 1)
    # 训练神经网络
    n.train(List)
    # 保存权重值
    n.weights()
if __name__ == '__main__':
    BP()

既然保存了 我们训练后的权重，最后当然是使用了。其实和之前是一样的，就是初始权重不再是随机数而是我们之前保存的，然后只有正向传播。
 

class BPNN:
    def __init__(self, num_in, num_hidden, num_out):
        # 输入层，隐藏层，输出层的节点数
        self.num_in = num_in + 1  # 增加一个偏置结点
        self.num_hidden = num_hidden + 1  # 增加一个偏置结点
        self.num_out = num_out
        # 激活神经网络的所有节点（向量）
        self.active_in = [1.0] * self.num_in
        self.active_hidden = [1.0] * self.num_hidden
        self.active_out = [1.0] * self.num_out
        # 创建权重矩阵
        self.wight_in = makematrix(self.num_in, self.num_hidden)
        self.wight_out = makematrix(self.num_hidden, self.num_out)
        # 对权值矩阵赋初值
        f = open("getwights.txt", "r")
        a = f.readline()
        b = f.readline()
        listone = eval(a)
        listtwo = eval(b)
        f.close()
        for i in range(len(listone)):
            for j in range(len(listone[i])):
                self.wight_in[i][j] = listone[i][j]
        for i in range(len(listtwo)):
            for j in range(len(listtwo[i])):
                self.wight_out[i][j] = listtwo[i][j]

        self.co = makematrix(self.num_hidden, self.num_out)
        # 信号正向传播

    def update(self, inputs):
        if len(inputs) != self.num_in - 1:
            raise ValueError('与输入层节点数不符')
        # 数据输入输入层
        for i in range(self.num_in - 1):
            # self.active_in[i] = sigmoid(inputs[i])  #或者先在输入层进行数据处理
            self.active_in[i] = inputs[i]  # active_in[]是输入数据的矩阵
        # 数据在隐藏层的处理
        for i in range(self.num_hidden - 1):
            sum = 0.0
            for j in range(self.num_in):
                sum = sum + self.active_in[i] * self.wight_in[j][i]
            self.active_hidden[i] = tanh(sum)  # active_hidden[]是处理完输入数据之后存储，作为输出层的输入数据
        # 数据在输出层的处理
        for i in range(self.num_out):
            sum = 0.0
            for j in range(self.num_hidden):
                sum = sum + self.active_hidden[j] * self.wight_out[j][i]
            self.active_out[i] = sigmoid(sum)  # 与上同理
        return self.active_out[:]
    # 测试
    def test(self, patterns):
        distingish=[]
        List_update=[]
        num=0
        sum=0
        for i in patterns:
            List_update.append(self.update(i[0]))
        sum=np.sum(List_update,axis=0)
        average=sum/(len(patterns))
        #print(average)
        for i in patterns:
            num += 1
            if (num <= testnums and self.update(i[0]) > average):
                distingish.append(True)
            if (num > testnums and self.update(i[0]) < average):
                distingish.append(True)
            print(i[0], '->', self.update(i[0]))
        print("正确率", len(distingish) / num)


# 实例
def BP():

    # 创建神经网络，3个输入节点，3个隐藏层节点，1个输出层节点
    n = BPNN(3, 3, 1)
    # 测试神经网络
    n.test(ListT)
if __name__ == '__main__':
    BP()

 后序

我写过一片关于Pyecharts的文章，是关于数据可视化，有兴趣的朋友可以去看看

https://blog.csdn.net/weixin_43341045/article/details/104137445，

关于这个数据的来源啊，可以很多种，我这里就介绍下爬虫。爬虫也有很多种库，写过一篇关于Selenium的爬虫https://blog.csdn.net/weixin_43341045/article/details/104014416。

还有一个9行代码爬取B站专栏图片（BeautifulSoup4）

https://blog.csdn.net/weixin_43341045/article/details/104411456

     鄙人仅为一名普普通通大二学生，才学浅出，来此各地高人聚集处书写浅见，还望各位前辈高人多多指点海涵。我们诚邀各地有志之士加入我们的代码学习群交流：871352155（无论你会C/C++还是Java，Python还是PHP......有兴趣我们都欢迎你的加入，不过还请各位认真填写加群信息。群内目前多为大学生，打广告的先生女士就请不要步足了。我们希望有远见卓识的前辈能为即将步入社会的初犊提出建议指引方向。）