机器学习(分类回归问题)常用评估指标
文章目录
- 分类常用指标
-
- 基于混淆矩阵的评价指标
- AUC
- 回归模型常用评价指标
-
- 均误差方(MSE)
- 平均绝对误差(MAE)
- 平均绝对比例误差(MAPE)
- R方
分类常用指标
基于混淆矩阵的评价指标
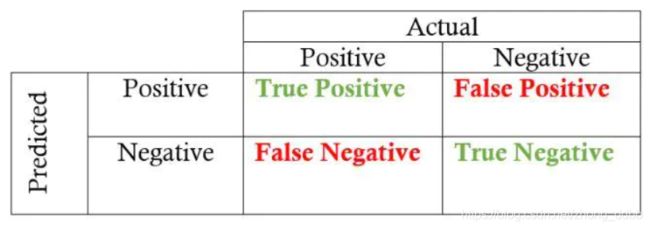
以二分类为例,由于模型预测存在误差,真实值和预测值之间存在差异,于是有以下四种情况:
- 真实值是positive,模型预测为positive(True Positive=TP)
- 真实值是positive,模型预测为negative(False Negative=FN)
- 真实值是negative,模型预测为positive(False Positive=FP)
- 真实值是negative,模型预测为negative(True Negative=TN)
将这四个指标一起呈现在表格中,得到的矩阵,称它为混淆矩阵(Confusion Matrix):
要保证一个模型的效果好,也就是希望混淆矩阵第二、四象限对应的位置的数值越多越好。
基于混淆矩阵,引出以下三种评价指标
| 名称 | 公式 | 意义 |
|---|---|---|
| 准确率 | Accurancy = T P + T N T P + T N + F P + F N \frac{TP+TN}{TP+TN+FP+FN} TP+TN+FP+FNTP+TN | 模型所有的正确预测结果占总数的比例 |
| 精确率 | precision= T P T P + F P \frac{TP}{TP+FP} TP+FPTP | 精确率是针对我们预测结果而言的,它表示的是预测为正的样本中有多少是真正的正样本。精确率低说明存在大量的假正例(FP)。 |
| 召回率 | Recall= T P T P + F N \frac{TP}{TP+FN} TP+FNTP | 召回率是针对我们原来的样本而言的,表示的是样本中的正例有多少被预测正确了。 |
基于精确率和召回率,又引入了F1 Score,在样本不平衡时,宜采用该评价指标。
F 1 S c o r e = 2 P R P + R F1 \quad Score = \frac{2PR}{P+R} F1Score=P+R2PR
其中,P代表Precision,R代表Recall。
F1-Score指标综合了Precision与Recall的产出的结果。F1-Score的取值范围从0到1的,1代表模型的输出最好,0代表模型的输出结果最差。
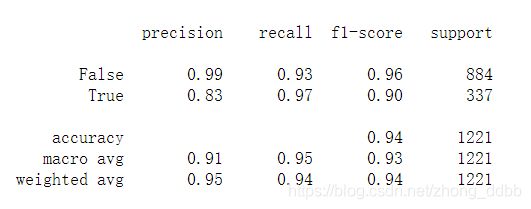
举例子分析,在sklearn中可以使用classification_report生成评价指标报告:
from sklearn.metrics import classification_report
print(classification_report(pred_y,y))
从上述结果看出:
-
正例样本的精确率为0.83,说明预测为正例的样本中只要83%是正真的正例,说明预测结果存在17%假正例(将0误分类为1)。
-
召回率0.97,说明训练样本数据中的正例有97%被预测对了。只有3%的正样本被预测为负类。
基于以上,我们应该思考为什么模型会将0误分类为1。
AUC
AUC(Area Under Curve),这里的Curve指的就是ROC曲线,AUC就是ROC曲线下面的面积,只适用于二分类。
在上述的混淆矩阵,引入两个概念:
-
True Positive Rate(TPR,真阳率),所有真实类别为1的样本中,预测类别为1的比例,计算公式如下:
T P R = T P T P + F N TPR = \frac{TP}{TP+FN} TPR=TP+FNTP -
False Positive Rate(FPR, 伪阳率),所有真实类别为0的样本中,预测类别为1的比例,计算公式如下:
F P R = F P T P + T N FPR = \frac{FP}{TP+TN} FPR=TP+TNFP
接下来通过例子说明如何计算AUC。数据来源:机器学习基础:AUC
(1)对于二分类问题,对于预测结果(概率)进行从大到小排序:
(2)分别以从小到大的预测概率作为阈值,进行分类,如以0.2作为阈值,则21,18号样本为负例,其余样本均为正例。取不同的阈值得到不同的混淆矩阵。得到不同的(TPR,FPR)。
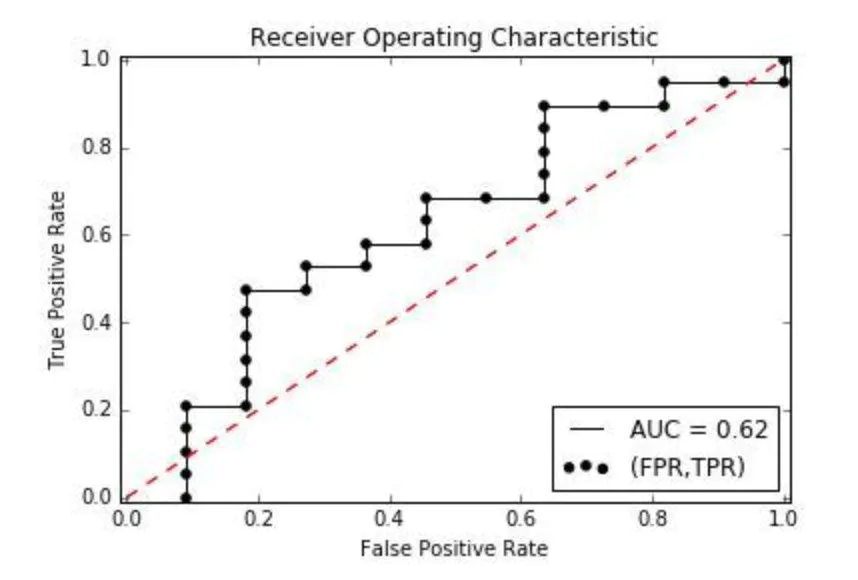
(3)将这些(TPR,FPR)在坐标中画出来。
将这些点平滑的画出,得到ROC曲线。AUC就是ROC曲线下面的面积。
最后说说AUC的优势,AUC的计算方法同时考虑了分类器对于正例和负例的分类能力,在样本不平衡的情况下,依然能够对分类器作出合理的评价。
sklearn相关函数
import numpy as np
from sklearn import metrics
y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
print(fpr,'\n',tpr,'\n',thresholds)
print(metrics.auc(fpr,tpr))
在这里插入图片描述
回归模型常用评价指标
均误差方(MSE)
所有样本的样本误差的平方的均值
M S E = 1 m ∑ ( y i − y ^ i ) 2 MSE = \frac{1}{m} \sum(y_i -\hat y_i)^2 MSE=m1∑(yi−y^i)2
sklearn 相关函数:
from sklearn.metrics import mean_squared_error
平均绝对误差(MAE)
所有样本的样本误差的绝对值的均值
M A E = 1 m ∑ ∣ y i − y ^ i ∣ MAE = \frac{1}{m} \sum|y_i - \hat y_i| MAE=m1∑∣yi−y^i∣
sklearn 相关函数:
from sklearn.metrics import mean_absolute_error
平均绝对比例误差(MAPE)
所有样本的样本误差的绝对值占实际值的比例,mape越接近0,模型越准确。
M A P E = 100 % n ∑ ∣ y i − y ^ i y i ∣ MAPE = \frac{100 \%}{n} \sum |\frac{y_i - \hat y_i}{y_i}| MAPE=n100%∑∣yiyi−y^i∣
R方
因变量的方差能被自变量解释的程度,R方越接近1,则代表自变量对因变量的解释度越高。
R 2 = 1 − M S E ( y , y ^ ) V a r ( y ) R^2 = 1- \frac{MSE(y,\hat y)}{Var(y)} R2=1−Var(y)MSE(y,y^)
sklearn 相关函数:
from sklearn.metrics import r2_score