自然语言处理（NLP）项目的基本流程

摘要：刚入门自然语言处理的小伙伴，或者说已经接触了一段时间，但是一直不能够对自然语言处理项目的整个流程有一个大方向的把握，不知道自己目前所研究的点，是处于NLP项目的流程的哪部分，可以通过此文章来了解一下。

一、基本流程

1. 分词
   英文通过空格或者标点符号，就可以将词分开；而中文的分词会涉及很多问题（未登录词问题、分词歧义问题、分词不一致问题），所以会有各种不同分词的算法。

2. 清洗
   我们需要对文本中无用的或者对理解文本没意义的字符进行清洗
   1）无用的标签：

   
   2）特殊符号：！。。。
   3）停用词：a an the
   4）大写转小写

3. 标准化
   在英文中进行标准化处理，就是将多个单词统一为同一个单词。
   例如：apple和apples都代表的是苹果，所以在文中不管是遇到apple还是apples，我们都用apple来统一表示。go gone went 都代表去的意思，同理，我们都用go来统一表示。

4. 特征提取
   将标准化之后的词，表示为向量的形式。

5. 建模
   各种AI的算法

6. 评估
   对模型进行评估，选择最优的模型。

二、分词

分词工具

• Jieba分词 https://github.com/fxsjy/jieba
• SnowNLP https://github.com/isnowfy/snownlp
• LTP http://www.ltp-cloud.com/
• HanNLP https://github.com/hankcs/HanLP/
• ……

例子：“南京市长江大桥”

词典：["南京","市长","大桥","长江","江","市"]

我们有这样一句话"南京市长江大桥"，有一个词典[“南京”,“市长”,“江”,“大桥”,“长江”]，怎么通过词典来进行分词呢？

2.1 前向最大匹配（forward-max matching）

前向最大匹配的前向意思是说，从前往后匹配。最大意思是说，我们匹配的词的长度越大越好，也就是这句话中分出来的词的数量越少越好。
这里，我们假设这个最大长度max_len = 5:

第一轮搜索：
①"南京市长江 大桥" 词典中没有南京市长江这个词，匹配失败
②"南京市长 江大桥" 词典中没有南京市长这个词，匹配失败
③"南京市长江大桥" 词典中没有南京市这个词，匹配失败
④"南京市长江大桥" 词典中有南京这个词，匹配成功，去除
句子变为：“市长江大桥”

第二轮搜索：
①"市长江大桥" 词典中没有市长江大桥这个词，匹配失败
②"市长江大桥" 词典中没有市长江大这个词，匹配失败
③"市长江大桥" 词典中没有市长江这个词，匹配失败
④"市长江大桥" 词典中有市长这个词，匹配成功，去除
句子变为：“江大桥”

第三轮搜索（句子长度已不足5，将max_len改为3）：
①"江大桥" 词典中没有江大桥这个词，匹配失败
②"江大桥"" 词典中没有江大这个词，匹配失败
③"江大桥" 词典中有江这个词，匹配成功，去除
句子变为：“大桥”

第四轮搜索：
①"大桥" 词典中有大桥这个词，匹配成功，去除
句子变为：""，说明已经处理完毕

最终结果：“南京 / 市长 / 江 / 大桥”

这个结果虽然勉强可以接受，可以认为它说的意思是，南京的市长名字叫江大桥，但是明显跟我们想要表达的或者想要理解的意思不一样，这就有了分词的歧义问题。
如果我们的词典里有南京市这个词，那么结果就是"南京市/长江/大桥"。

2.2 后向最大匹配（backward-max matching）

后向最大匹配的后向意思是说，从后往前匹配。最大意思同样是说，我们匹配的词的长度越大越好。
这里，我们同样假设这个最大长度max_len = 5:

第一轮搜索：
①"南京市长江大桥 " 词典中没有市长江大桥这个词，匹配失败
②"南京市长江大桥 " 词典中没有长江大桥这个词，匹配失败
③"南京市长江大桥 " 词典中没有江大桥这个词，匹配失败
④"南京市长江大桥 " 词典中有大桥这个词，匹配成功，去除
句子变为：“南京市长江”

第二轮搜索：
①"南京市长江 " 词典中没有南京市长江这个词，匹配失败
②"南京市长江 " 词典中没有京市长江这个词，匹配失败
③"南京市长江 " 词典中没有市长江这个词，匹配失败
④"南京市长江 " 词典中有长江这个词，匹配成功，去除
句子变为：“南京市”

第三轮搜索（句子长度已不足5，将max_len改为3）：
①"南京市 " 词典中没有南京市这个词，匹配失败
②"南京市 " 词典中没有京市这个词，匹配失败
③"南京市 " 词典中有市这个词，匹配成功，去除
句子变为：“南京”

第四轮搜索：
①"南京 " 词典中有南京这个词，匹配成功，去除
句子变为：""，说明已经处理完毕

最终结果：“南京 / 市 / 长江 / 大桥”

相同的话，相同的词典，分出来的效果却不一样，导致了歧义问题。统计结果表明，单纯使用后向最大匹配算法的错误率略低于正向最大匹配算法。

python代码实现：

# -*- coding: utf-8 -*-
# Author    : 不凡不弃
# Datetime  : 2020/5/27 0027 13:39
# description   : 分词

dictionaries = ["南京", "市长", "大桥", "长江", "江", "市"]


# 前向最大匹配
def forward_max_matching(text, max_len=5):
    result = []
    text_ = text
    index = max_len

    while len(text_) > 0:

        if index == 0:
            print("分词失败，词典中没有这个词")
            return []

        if text_[:index] in dictionaries:
            result.append(text_[:index])
            text_ = text_[index:]
            index = 5
        else:
            index = index - 1

    return "".join(word + "/" for word in result)


# 后向最大匹配
def backward_max_matching(text, max_len=5):
    result = []
    text_ = text
    index = max_len

    while len(text_) > 0:

        if index == 0:
            print("分词失败，词典中没有这个词")
            return []
        # print(text_[-index:])
        if text_[-index:] in dictionaries:
            result.insert(0, text_[-index:])
            # result.append(text_[-index:])
            text_ = text_[:-index]
            index = 5
        else:
            index = index - 1

    return "".join(word + "/" for word in result)


if __name__ == '__main__':
    content = "南京市长江大桥"
    forward_result = forward_max_matching(content)
    print("forward_result:", forward_result)
    backward_result = backward_max_matching(content)
    print("backward_result:", backward_result)

以上分词算法的缺点有哪些？

• 不能够细分（有可能效果更好）
• 结果是局部最优
• 效率低（词典列表如果很长的话，效率会很低）
• 歧义（不能考虑语义）

2.3 考虑语义

例子：“经常有意见分歧”

词典：["经常","有","意见","意","见","有意见","分歧","分","歧"]
概率P(x)：{"经常":0.08,"有":0.04,"意见":0.08,"意":0.01,"见":0.005,"有意见":0.002,"分歧":0.04,"分":0.02, "歧":0.005}

概率P(x)代表的是该词x在我们日常生活所见的文本中出现的概率。

step1：我们根据词典，找出所有可能的分词情况，如下：

• 经常 / 有意见 / 分歧
• 经常 / 有意见 / 分 / 歧
• 经常 / 有 / 意见 / 分歧
• 经常 / 有 / 意见 / 分 / 歧

step2：我们如果有一个语言模型，可以计算出每种情况属于中文语法的概率，我们选择最高的，也就是效果最好的。例如第一个情况的概率为：
$$P(经常,有意见,分歧)=P(经常)\ast P(有意见)\ast P(分歧)=0.08\ast 0.02\ast 0.04=0.000064$$
我们考虑到这样算的话值会很小，很容易造成内存溢出，所以引入$-ln$来计算，也就是由算P(x)的最大值变为算$-ln(P(x))$的最小值，

-ln(P(x))：{"经常":2.52,"有":3.21,"意见":2.52,"意":4.6,"见":5.29,"有意见":6.21,"分歧":3.21,"分":3.9, "歧":5.29}

$$-ln(P(经常,有意见,分歧))=-ln(P(经常)\ast P(有意见)\ast P(分歧))=-ln(P(经常)-ln(有意见)-ln(分歧)=2.52+6.21+3.21=11.94$$

但是这两步下来时间复杂度太高，并不可取。怎么能够优化一下呢？就是接下来的维特比算法

维特比算法(viterbi)

例子：“经常有意见分歧”

我们仍然是有以下几个数据：

词典：["经常","有","意见","意","见","有意见","分歧","分","歧"]
概率P(x)：{"经常":0.08,"有":0.04,"意见":0.08,"意":0.01,"见":0.005,"有意见":0.002,"分歧":0.04,"分":0.02, "歧":0.005}
-ln(P(x))：{"经常":2.52,"有":3.21,"意见":2.52,"意":4.6,"见":5.29,"有意见":6.21,"分歧":3.21,"分":3.9, "歧":5.29}

• 如果某个词不在字典中，我们将认为其$-ln(P(x))$值为20。

我们构建以下的DAG(有向图），每一个边代表一个词，我们将-ln(P(x))的值标到边上，

求$-ln(P(x))$的最小值问题，就转变为求最短路径的问题。

由图可以看出，路径 0—>②—>③—>⑤—>⑦ 所求的值最小，所以其就是最优结果：经常 / 有 / 意见 / 分歧
那么我们应该怎样快速计算出来这个结果呢？

我们设$f(n)$代表从起点0到结点n的最短路径的值，所以我们想求的就是$f(7)$

，我们考虑到结点⑦有2条路径：

• 从结点⑤—>结点⑦：$f(7)=f(5)+3.21$
• 从结点⑥—>结点⑦：$f(7)=f(6)+5.29$

我们应该从2条路径中选择路径短的。

在上面的第1条路径中，$f(5)$还是未知的，我们要求$f(5)$，同理我们发现到结点⑤的路径有3条路径：

• 从结点②—>结点⑤：$f(5)=f(2)+6.21$
• 从结点③—>结点⑤：$f(5)=f(3)+2.52$
• 从结点④—>结点⑤：$f(5)=f(4)+20$

我们同样从3条路径中选择路径短的。以此类推，直到结点0，所有的路径值都可以算出来。我们维护一个列表来表示f(n)的各值：

结点	1	2	3	4	5	6	7
f(n)	20	2.52	5.73	25.73	8.25	12.5	11.46
结点的上一个结点	0	0	②	③	③	⑤	⑤

第2行代表从起点0到该结点的最短路径的值，第3行代表在最短路径中的该节点的上一个结点。通过表，我们可以找到结点⑦的上一个结点⑤，结点⑤的上一个结点③，结点③的上一个结点②，结点②的上一个结点0，即路径：0—>②—>③—>⑤—>⑦

python代码实现：

# -*- coding: utf-8 -*-
# Author    : 不凡不弃
# Datetime  : 2020/5/27 0027 13:39
# description   : 维特比算法(viterbi)
import math
import collections

# 维特比算法(viterbi)
def word_segmentation(text):
    ##################################################################################
    word_dictionaries = ["经常", "有", "意见", "意", "见", "有意见", "分歧", "分", "歧"]
    probability = {"经常": 0.08, "有": 0.04, "意见": 0.08, "意": 0.01, "见": 0.005, "有意见": 0.002, "分歧": 0.04, "分": 0.02,
                   "歧": 0.005}
    probability_ln = {key: -math.log(probability[key]) for key in probability}

    # 构造图的代码并没有实现，以下只是手工建立的图，为了说明 维特比算法
    ##################################################################################

    # 有向五环图，存储的格式：key是结点名，value是一个结点的所有上一个结点（以及边上的权重）
    graph = {
        0: {0: (0, "")},
        1: {0: (20, "经")},
        2: {0: (2.52, "经常"), 1: (20, "常")},
        3: {2: (3.21, "有")},
        4: {3: (20, "意")},
        5: {2: (6.21, "有意见"), 3: (2.52, "意见"), 4: (20, "见")},
        6: {5: (3.9, "分")},
        7: {5: (3.21, "分歧"), 6: (5.29, "歧")}
    }
    # 保存结点n的f(n)以及实现f(n)的上一个结点
    f = collections.OrderedDict()

    for key, value in graph.items():
        # 如果该节点的上一个结点还没有计算f(n)，则直接比较大小；如果计算了f(n)，则需要加上f(n)
        # 从该节点的所有上一个结点中选择f(n)值最小的
        min_temp = min((pre_node_value[0], pre_node_key) if pre_node_key not in f else (
            pre_node_value[0] + f[pre_node_key][0], pre_node_key) for pre_node_key, pre_node_value in value.items())
        f[key] = min_temp

    print(f)
    # 结果：OrderedDict([
    # (0, (0, 0)), (1, (20, 0)), (2, (2.52, 0)), (3, (5.73, 2)),
    # (4, (25.73, 3)), (5, (8.25, 3)), (6, (12.15, 5)), (7, (11.46, 5))
    # ])

    # 最后一个结点7
    last = next(reversed(f))
    # 第一个结点0
    first = next(iter(f))
    # 保存路径，最后一个结点先添入
    result = [last, ]
    # 最后一个结点的所有前一个结点
    pre_last = f[last]

    # 没到达第一个结点就一直循环
    while pre_last[1] is not first:
        # 加入一个路径结点X
        result.append(pre_last[1])
        # 定位到路径结点X的上一个结点
        pre_last = f[pre_last[1]]
    # 第一个结点添入
    result.append(first)

    print(result)
    # 结果：[7, 5, 3, 2, 0]

    text_result = []
    # 找到路径上边的词
    for i, num in enumerate(result):
        if i + 1 == len(result):
            break
        # print(i, num, result[i + 1])
        word = graph[num][result[i + 1]][1]
        # print(word)
        text_result.append(word)
    # 翻转一下
    text_result.reverse()

    return "".join(word + "/" for word in text_result)


if __name__ == '__main__':

    content = "经常有意见分歧"
    word_segmentation_result = word_segmentation(content)
    print("word_segmentation_result:", word_segmentation_result)

三、过滤词

对于一个自然语言处理任务，我们通常先把停用词以及出现频率很低的词过滤掉。

• 停用词，对于理解文章没有太大意义的词，比如"the"、“an”、“his”、“their”，但是，也需要考虑自己的应用场景，来决定过滤哪些停用词。停用词下载：链接：https://pan.baidu.com/s/1XRNPAAQIkaNO-8qb_DdctQ 提取码：86o0

• 出现频率很低的词，比如1万个单词的文章里它只出现了一两次。

如果不过滤掉它们，很可能对我们的语言模型产生负面的影响。

四、单词和句子的表示

词典：["我们","又","去","爬山","今天","你们","昨天","跑步"]

假设我们有以上的一个词典，怎么用编码来唯一表示下面这几个词呢？
我们 、爬山 、 跑步、 昨天

4.1 one-hot编码

one-hot编码的思想就是，查询词典，找到该词在词典中的位置，编码的时候将该位置写为1，其余位置写0。比如我们这样表示：

我们	爬山	跑步	昨天
(1,0,0,0,0,0,0,0)	(0,0,0,1,0,0,0,0)	(0,0,0,0,0,0,0,1)	(0,0,0,0,0,0,1,0)

我们发现编码好的向量是一个8维的向量，即词典的大小（词典中有8个词）。

怎么用编码来唯一表示下面这几个句子呢？

• 我们 今天 去 爬山
• 你们 昨天 跑步
• 你们 又去 爬山 又去 跑步

同样用one-hot思想，比如我们这样表示：

我们 今天 去 爬山	你们 昨天 跑步	你们 又 去 爬山 又 去 跑步
(1,0,1,1,1,0,0,0)	(0,0,0,0,0,1,1,1)	(0,1,1,1,0,1,0,1)

我们发现编码好的向量仍是一个8维的向量，即词典的大小（词典中有8个词）。但是第三句话你们 又去 爬山 又去 跑步的 又 和 去 只能标记一遍，且句子正确顺序没有表达出来。

我们如果考虑次数如下：

我们 今天 去 爬山	你们 昨天 跑步	你们 又 去 爬山 又 去 跑步
(1,0,1,1,1,0,0,0)	(0,0,0,0,0,1,1,1)	(0,2,2,1,0,1,0,1)

仍存在的问题：没有考虑语义，看不出来真正哪个词的重要性高，也就是说并不是出现的越多就越重要，并不是出现的越少越不重要。接下来的tf-idf解决这个问题。

4.2 TF-IDF

tf-idf公式：$tfidf(w)=tf(d,w)\ast idf(w)$

• $tfidf(w)$代表词$w$在当前文档（句子）的重要性
• $tf(d,w)$代表文档（句子）$d中w$的词频，跟上一步一样，考虑了次数。
• $idf(w)$则是考虑单词的重要性，大致思想就是，有些单词，它在很多的文档（句子）中都会出现，比如he、the、a、here，一旦一些词在每个文档（句子）中都出现，我们反而不觉得它重要；相反，如果一个词没有在其他文档（句子）中出现，却在当前文档（句子）中出现，说明它在当前文档（句子）中的重要性是比较大的。$idf(w)$展开就是：

$$idf(w)=ln\frac{N}{N(w)}$$
$N$代表语料中的文档（句子）总数，$N(w)$代表词$w$出现在多少个文档（句子）中。比如有100个文档（句子），$N=100$，词$w$在10个文档（句子）中出现，$N(w)=10$，则$idf(w)=ln10$。也就是说词$w$出现的文档（句子）数越少，词$w$在该文档（句子）的重要性越大。

词典：["我们","又","去","爬山","今天","你们","昨天","跑步"]

怎么用$tfidf(w)$来表示下面这几个句子呢？

• 我们 今天 去 爬山
• 你们 昨天 跑步
• 你们 又 去 爬山 又 去 跑步

我们可以表示如下：

我们 今天 去 爬山	你们 昨天 跑步	你们 又 去 爬山 又 去 跑步
($ln3,0,ln\frac{3}{2},ln\frac{3}{2},ln3,0,0,0$)	($0,0,0,0,0,ln\frac{3}{2},ln3,ln\frac{3}{2}$)	($0,2ln3,2ln\frac{3}{2},ln\frac{3}{2},0,ln\frac{3}{2},0,ln\frac{3}{2}$)

存在的问题

以上的两个表示方法one-hot编码和TF-IDF，存在2个缺点：

• 词与词之间的相似度表达不出来

我们	爬山	跑步	昨天
(1,0,0,0,0,0,0,0)	(0,0,0,1,0,0,0,0)	(0,0,0,0,0,0,0,1)	(0,0,0,0,0,0,1,0)

通过5.1 欧式距离公式，我们算得以上两两单词之前的相似度都是$\sqrt{2}$，通过5.2 余弦相似度公式，算得以上两两单词之前的相似度都是$0$，这显然都不符合实际情况

• 向量维度太高，如果词典中有1万个单词，则一个单词的向量维度就是1万

接下来的分布式表示方法词向量解决这2个问题

4.3 词向量（Word embedding）

如图，我们可以将8维的one-hot编码转变为4维的词向量：

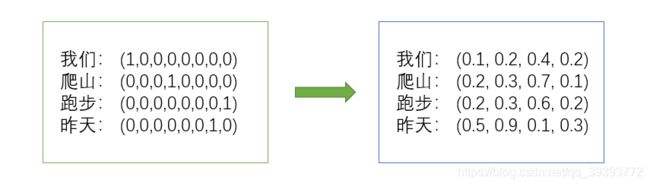
词向量的每一位上都有一个非零的数，我们再通过5.1 欧式距离公式，算得：
$$d_{(我们,爬山)}=\sqrt{0.12}$$
词向量并不像之前的one-hot编码和TF-IDF可以直接简单的计算出来，它是需要深度学习模型来训练出来的，如图：

五、句子的相似度(Sentence similarity)

5.1 欧式距离

欧式距离公式：$d=|s_1-s_2|$

其中$d$代表两个句子之间的距离，距离越小，代表两个句子的相似度越高，$s_1$和$s_2$分别代表两个句子的向量。

如果$s_1=(x_1,x_2,x_3)、s_2=(y_1,y_2,y_3)$，则
$$d=\sqrt{(x_1-y_1{)}^2+(x_2-y_2{)}^2+(x_3-y_3{)}^2}$$

• $s_1$：“我们今天去爬山” = (1,0,1,1,1,0,0,0)
• $s_2$：“你们昨天跑步” = (0,0,0,0,0,1,1,1)
• $s_3$：“你们又去爬山又去跑步” = (0,2,2,1,0,1,0,1)

$s_1$和$s_2$的距离：$d(s_1,s_2)=\sqrt{1+0+1+1+1+1+1+1}=\sqrt{7}$

$s_1$和$s_3$的距离：$d(s_1,s_3)=\sqrt{1+4+1+0+1+1+0+1}=\sqrt{9}$

$s_2$和$s_3$的距离：$d(s_2,s_3)=\sqrt{0+4+4+1+0+0+1+0}=\sqrt{10}$

则我们认为$s_1$与$s_2$的相似度最高，即$sim(s_1,s_2)>sim(s_1,s_3)>sim(s_2,s_3)$

欧式距离只考虑了向量的大小，并没有考虑向量的方向，余弦相似度则考虑了方向。

5.2 余弦相似度（Cosine similarity）

余弦相似度公式：$$d=\frac{s_1\cdot s_2}{|s_1|\ast |s_2|}$$

其中$s_1\cdot s_2$代表两个向量的内积，$|s_1|\ast |s_2|$代表两个向量距离的乘积。d越大，相似度越大，与欧式距离是相反的。

如果$s_1=(x_1,x_2,x_3)、s_2=(y_1,y_2,y_3)$，则
$$d=\frac{x_1{y}_1+x_2{y}_2+x_3{y}_3}{\sqrt{x_1^2+x_2^2+x_3^2}\ast \sqrt{y_1^2+y_2^2+y_3^2}}$$

• $s_1$：“我们今天去爬山” = (1,0,1,1,1,0,0,0)
• $s_2$：“你们昨天跑步” = (0,0,0,0,0,1,1,1)
• $s_3$：“你们又去爬山又去跑步” = (0,2,2,1,0,1,0,1)

$s_1$和$s_2$的相似度：$d(s_1,s_2)=0$

$s_1$和$s_3$的相似度：$d(s_1,s_3)=\frac{2+1}{2\ast \sqrt{11}}$

$s_2$和$s_3$的相似度：$d(s_2,s_3)=\frac{2}{\sqrt{3}\ast \sqrt{11}}$

则我们认为$s_1$与$s_3$的相似度最高，即$sim(s_1,s_3)>sim(s_2,s_3)>sim(s_1,s_2)$