二维矩形件排样算法之最低水平线搜索算法实现
最低水平线搜索算法的实现(Python)
之前有一篇文章介绍了二维矩形排样基本算法中的最低水平线算法(点击传输门),本文介绍最低水平线搜索算法
最低水平线算法的缺陷
最低水平线法在排样时,每排入一个零件就会寻找当前水平线集中的最低水平线,但当最低水平线的宽度小于零件宽度时就会执行提升水平线的操作,每提升一次水平线就会造成一部分无法使用的空闲区域,因此水平线提升的次数过多会造成很多无法利用的空闲区域,最终导致该算法的排样效果不佳。而有些情况下,由于当前所选的零件的面积较大,最低水平线宽度不够,排不下该零件,但却可以排放其他面积较小或宽度较窄的未排零件,如果此时盲目提升水平线,会导致很多不必要的浪费,基于这个原因,一些学者提出了最低水平线搜索算法,即当当前所选零件排放不下时,算法转向搜索其他未排零件,当且仅当所有未排零件都排放不下时,再提升水平线。
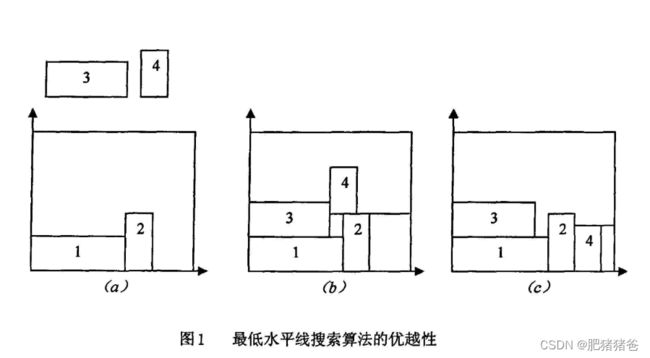
如图1(a) 所示,将矩形件1和2排入之后,此时的最低水平线的宽度小于零件3的长度,按照算法规则将最低水平线提升,则提升后得到的新水平线下面产生了大块无法利用的空闲区域,而且该空闲区域可以排放零件4,但由于算法的缺陷将此块区域白白浪费,如图1(b)所示,最低水平线法排完4个零件提升了2次水平线,产生了2块不可利用的空闲区域。而最低水平线搜索算法在遇到图1(a)所示的情况时,不立即提升最低水平线,而转向搜索其后面的零件4,如果能排下,就将其排入,排不下则继续往后搜索,直到所有零件都排不下时再提升水平线,图1(c ) 所示用最低水平线搜索算法排完4个零件,水平线提升1次,造成的浪费面积远小于原始算法。
代码如下, 对之前的部分代码做了调整,并加入了矩形件搜索和旋转的逻辑
import numpy as np
import matplotlib.pyplot as plt
# 水平线类(起始x位置,终止x位置,高度)
class OutLine:
def __init__(self, origin, end, height):
self.origin = origin
self.end = end
self.height = height
def __str__(self):
return "OutLine:origin:{}, end:{}, height:{}".format(self.origin, self.end, self.height)
# 矩形物品类(宽度,高度,编号)
class Product:
def __init__(self, w, h, num=0):
self.w = w
self.h = h
self.num = num
def __str__(self):
return "product:w:{}, h:{}, num:{}".format(self.w, self.h, self.num)
# 根据长度搜索矩形件(找出宽度小于目标长度的首个矩形件)
@staticmethod
def search_by_width(target_width, data):
for index, p in enumerate(data):
if p.w <= target_width:
return index
return None
# 根据长度搜索矩形件(找出宽度或高度小于目标长度的首个矩形件)
@staticmethod
def search_by_size(target_width, data):
for index, p in enumerate(data):
if p.w <= target_width or p.h <= target_width:
return index
return None
# 旋转90度并返回新对象
def rotate_new(self):
return Product(self.h, self.w, self.num)
# 布局类
class RectLayout:
def __init__(self, width, line_list=[]):
self.width = width
# 水平线集合(起始x位置,终止x位置,高度)
self.line_list = line_list
# 水平线(起始x位置,终止x位置,高度)
self.lowest_line = None
# 水平线索引(起始x位置,终止x位置,高度)
self.lowest_line_idx = 0
# 最终位置结果[[矩形件编号,左下角横坐标,左下角纵坐标,矩形件宽度,矩形件高度], ...]
self.result_pos = []
# 板材利用率
self.ratio = 0.0
# 初始化水平线集合(起始x位置,终止x位置,高度)
def init_line_list(self, origin, end, height):
init_line = OutLine(origin, end, height)
self.line_list = [init_line]
self.lowest_line = init_line
self.lowest_line_idx = 0
# 提升最低水平线
def enhance_line(self, index):
if len(self.line_list) > 1:
# 获取高度较低的相邻水平线索引,并更新水平线集
neighbor_idx = 0
if index == 0:
neighbor_idx = 1
elif index + 1 == len(self.line_list):
neighbor_idx = index - 1
else:
# 左边相邻水平线
left_neighbor = self.line_list[index - 1]
# 右边相邻水平线
right_neighbor = self.line_list[index + 1]
# 选择高度较低的相邻水平线,左右相邻水平线高度相同时,选择左边相邻的水平线
if left_neighbor.height < right_neighbor.height:
neighbor_idx = index - 1
elif left_neighbor.height == right_neighbor.height:
if left_neighbor.origin < right_neighbor.origin:
neighbor_idx = index - 1
else:
neighbor_idx = index + 1
else:
neighbor_idx = index + 1
# 选中的高度较低的相邻水平线
old = self.line_list[neighbor_idx]
# 更新相邻水平线
if neighbor_idx < index:
self.line_list[neighbor_idx] = OutLine(old.origin, old.end + self.line_width(index), old.height)
else:
self.line_list[neighbor_idx] = OutLine(old.origin - self.line_width(index), old.end, old.height)
# 删除当前水平线
del self.line_list[index]
# 按位置更新水平线
def update_line_list(self, index, new_line):
self.line_list[index] = new_line
# 按位置插入水平线(插在某索引位置后面)
def insert_line_list(self, index, new_line):
new_lists = []
if len(self.line_list) == index + 1:
new_lists = self.line_list + [new_line]
else:
new_lists = self.line_list[:index + 1] + [new_line] + self.line_list[index + 1:]
self.line_list = new_lists
# 计算水平线宽度
def line_width(self, index):
line = self.line_list[index]
return line.end - line.origin
# 找出最低水平线(如果最低水平线不止一条则选取最左边的那条)
def find_lowest_line(self):
# 最低高度
lowest = min([_l.height for _l in self.line_list])
# 最低高度时,最小开始横坐标
origin = min([_l.origin for _l in self.line_list if _l.height == lowest])
for _idx, _line in enumerate(self.line_list):
if _line.height == lowest and _line.origin == origin:
self.lowest_line_idx = _idx
self.lowest_line = _line
# 清空水平线集合
def empty_line_list(self):
self.line_list.clear()
# 计算最高水平线高度,即所用板材最大高度
def cal_high_line(self):
max_height = max([ll.height for ll in self.line_list])
return max_height
# 将矩形物品排样
def packing(self, _pro: Product):
# 最低水平线宽度
lowest_line_width = self.line_width(self.lowest_line_idx)
# 对矩形件排样
self.result_pos.append([_pro.num, self.lowest_line.origin, self.lowest_line.height, _pro.w, _pro.h])
# 更新水平线集
new_line1 = OutLine(self.lowest_line.origin, self.lowest_line.origin + _pro.w, self.lowest_line.height + _pro.h)
new_line2 = OutLine(self.lowest_line.origin + _pro.w, self.lowest_line.origin + lowest_line_width, self.lowest_line.height)
self.update_line_list(self.lowest_line_idx, new_line1)
if lowest_line_width - _pro.w > 0:
self.insert_line_list(self.lowest_line_idx, new_line2)
# 计算板材利用率
def cal_used_ratio(self):
# 计算板材利用率
used_area = 0
for _p in self.result_pos:
used_area += _p[3] * _p[4]
# 板材使用最大高度
max_high = self.cal_high_line()
# 利用率
if max_high > 0:
self.ratio = round((used_area * 100) / (self.width * max_high), 3)
return used_area, self.ratio
# 主方法
if __name__ == "__main__":
# 板材宽度
container_width = 10
# 矩形物品数量
item_num = 25
# 初始化矩形物品尺寸,也可以随机生成
# item_sizes = np.random.randint(1, 8, size=(item_num, 2)).tolist()
item_sizes = [[3, 1], [4, 4], [1, 1], [2, 3], [2, 4], [3, 4], [1, 4], [2, 2], [3, 3], [3, 1], [4, 2], [3, 1],
[3, 1], [3, 2], [4, 2], [1, 2], [1, 3], [3, 4], [2, 3], [1, 1], [2, 1], [3, 2], [4, 3], [3, 2],
[4, 3]]
# 按面积对矩形物品尺寸排序
_item_sizes = sorted(item_sizes, key=lambda x: x[0] * x[1], reverse=True)
print(_item_sizes)
# 排样序号
ran = [i + 1 for i in range(item_num)]
print(ran)
# 矩形物品列表
products = []
for idx in range(item_num):
products.append(Product(_item_sizes[idx][0], _item_sizes[idx][1], ran[idx]))
# 初始化布局类
layout = RectLayout(width=container_width)
# 初始化水平线集
layout.init_line_list(0, container_width, 0)
while products:
# 最低水平线及其索引
layout.find_lowest_line()
# 可用长度
available_width = layout.line_width(layout.lowest_line_idx)
# 候选物品索引
# candidate_idx = Product.search_by_width(available_width, products)
candidate_idx = Product.search_by_size(available_width, products)
if candidate_idx is not None:
# 候选物品
pro = products[candidate_idx]
# 宽度放不下时,对矩形件进行旋转
if pro.w > available_width >= pro.h:
pro = pro.rotate_new()
# 将候选物品排样
layout.packing(pro)
# 剔除已经排样的物品
products.pop(candidate_idx)
else:
# 最低水平线宽度小于要排样矩形宽度,提升最低水平线
layout.enhance_line(layout.lowest_line_idx)
# 计算板材利用率
_area, _ratio = layout.cal_used_ratio()
print("used_area: {}".format(_area))
print("ratio: {}%".format(_ratio))
# 计算最高水平线高度,即所用板材最大高度
container_height = layout.cal_high_line()
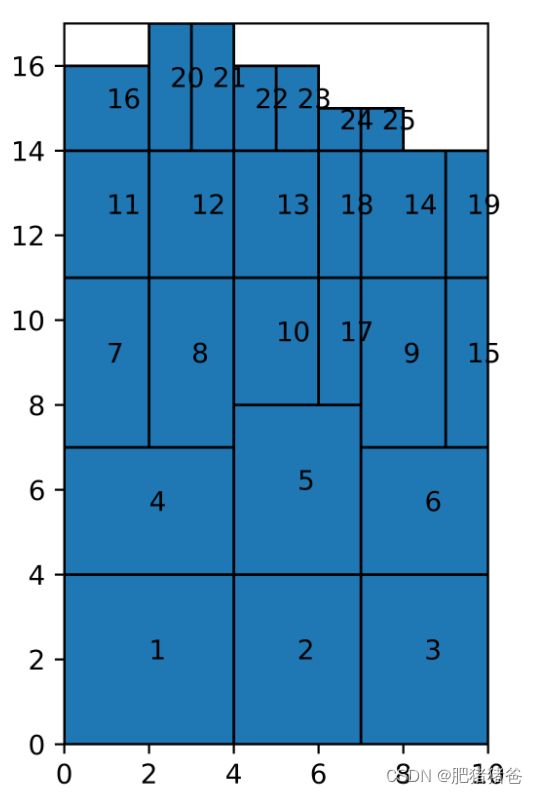
# 绘制排样布局
fig = plt.figure()
plt.xlim(0, container_width)
plt.ylim(0, container_height)
plt.axis("off")
ax = fig.add_subplot(111, aspect='equal')
ax.set_xlim(0, container_width)
ax.set_ylim(0, container_height)
for pos in layout.result_pos:
ax.add_patch(
plt.Rectangle(
(pos[1], pos[2]), # 矩形左下角
pos[3], # 长
pos[4], # 宽
alpha=1,
edgecolor='black',
linewidth=1
)
)
# 物品编号
ax.text(pos[1] + pos[3] / 2, pos[2] + pos[4] / 2, "{}".format(pos[0]), transform=ax.transData)
# plt.show()
plt.savefig('lowest_horizontal_line_search.png', dpi=800)
代码托管在gitee,项目持续更新
本文参考了合肥工业大学硕士论文《启发式算法在矩形件优化排样中的应用》
作者这水平有限,有不足之处欢迎留言指正