基于 Java 机器学习自学笔记 （第56-57天：kMeans 聚类）

注意：本篇为50天后的Java自学笔记扩充，内容不再是基础数据结构内容而是机器学习中的各种经典算法。这部分博客更侧重与笔记以方便自己的理解，自我知识的输出明显减少，若有错误欢迎指正！

---

目录

一、算法解释

· 关于KMeans的那些需要注意的地方

二、一些数据结构说明

三、代码实现过程

1. 距离计算

2. 分簇

四、数据测试与进行外部评价

· 关于聚类的评价指标

（补充的57天内容）扩充的中心点查找策略

---

一、算法解释

        何为聚类，聚类不同于我们之前的kNN，是完全不同的机器学习任务。kNN属于一种监督学习，他会给你一些数据所属于的类别，然后通过学习这种关联，去试着预测某些案例属于何种类别。即kNN类别是预定义好类别的，是可训练的；而聚类则不会给类别，他只会给你数据的一系列属性，通过属性的相似性将某些实例聚合为一个可能的类别。

        例如用kNN中iris数据集来看，不再有类别一列，仅仅有孤单的数据作为预测类的依据。

@RELATION iris

@ATTRIBUTE sepallength	REAL
@ATTRIBUTE sepalwidth 	REAL
@ATTRIBUTE petallength 	REAL
@ATTRIBUTE petalwidth	REAL

@DATA
5.1,3.5,1.4,0.2
4.9,3.0,1.4,0.2
4.7,3.2,1.3,0.2
4.6,3.1,1.5,0.2
5.0,3.6,1.4,0.2
5.4,3.9,1.7,0.4
4.6,3.4,1.4,0.3
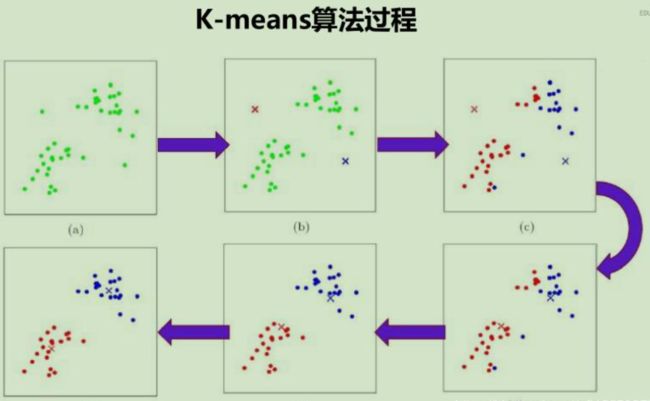
5.0,3.4,1.5,0.2

(下面我引用一张互联网上的图片，因为在很多博客都看到这图，不是很确定基本出处在哪)

         KMeans的过程可简单总结为以下的两个主要过程：

1. 定中心点
2. 初步划定类别

        这两个过程是循环的过程。假设如上图，设置k=2，最开始我们随机选择两个点作为中心点，然后将距离中心点最近的一些散点纳入这个中心点，这个过程叫做分簇。如此来看就能依据两个中心点就可将全图的散点初步地归类为两簇。但是由于初始化两中心点的随机性，这样的两类往往是不准确的，于是进一步我们求取各自类别点的重心，并且设置这些重心为新的中心点。

        确定了新的中心点后，再依据这些中心点对于全图散点进行分簇，这样就又确定了新的两簇，然后再求每类散点的重心，于是再得出新的中心点...（如此反复）

        直到满足下面的任何情况，即触发“收敛”条件，于是便结束代码：

1. 两次选取的中心点完全一致
2. 两次对散点的分类完全一致

· 关于KMeans的那些需要注意的地方

        KMeans也需要对数据信息归一化，这是为了避免量纲的影响，方便数据在同样的测试环境进行分簇，更好地表示“ 距离 ”。下列代码为简单起见就没有直接归一化，而直接将所有的四列属性不作处理地直接作为四维的向量参与距离计算与重心计算。

        KMeans问题最难的地方在于k的选取，在完全不得知数据应当是几类时，错误地给出k将会使得数据分类变得一塌糊涂。比如上面的过程，很明显人眼可以看出是两簇（k=2），但是如果将k设置为5，得到结果必然是一塌糊涂的。KNN的k选取可能不会特别地影响问题的最终结果，但是对于KMeans来说，这确实一个是关乎生死的、重要且麻烦的问题。有些高级算法可以自动地选择k的设置，但是作为基础聚类算法的KMeans，k必须要人为设置。

        同时，因为每次分簇是我们是依据每个散点到中心点的平均距离来确定的，因此任意选取点总是围绕中心点为一定半径范围内，因此KMeans很适合于球形数据（三维来看）

        KMeans作为基础数据，与KNN相同，都有很强的适应性。

二、一些数据结构说明

        今天我们测试依旧采用我KNN那篇的数据集，但是在处理时默认忽略类别属性。所以在后续代码中将常见：dataset.numAttributes() - 1的写法。

	/**
	 * Manhattan distance.
	 */
	public static final int MANHATTAN = 0;

	/**
	 * Euclidean distance.
	 */
	public static final int EUCLIDEAN = 1;

	/**
	 * The distance measure.
	 */
	public int distanceMeasure = EUCLIDEAN;

	/**
	 * A random instance;
	 */
	public static final Random random = new Random();

	/**
	 * The data.
	 */
	Instances dataset;

        基本的数据声明同KNN，因为我们依旧要使用随机数组，因此这里稍微重用了KNN的数据与代码。

	/**
	 * The number of clusters.
	 */
	int numClusters = 2;

	/**
	 * The clusters.
	 */
	int[][] clusters;

        numClusters就是KMeans的k，这里numClusters = 2，是一个默认值，后续代码中我们重设了其值为3（定义了个setter）

	/**
	 ******************************* 
	 * A setter.
	 ******************************* 
	 */
	public void setNumClusters(int paraNumClusters) {
		numClusters = paraNumClusters;
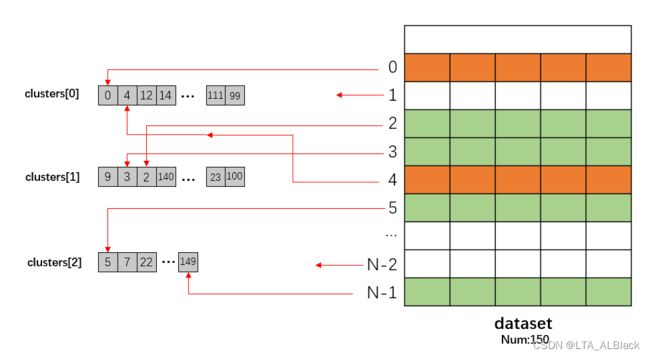
	}// Of the setter

        clusters是一个记录器，它记录了某簇管辖下的数据数组，例如clusters[1]就记录了1号分簇的全部数据情况。因为知道一个数据集下标后可以\(O(1)\)地访问数据集，所以我们存储数据都只存储下标即可。

         其实clusters主要功能只是为了最后打印数据用的。

		int[] tempOldClusterArray = new int[dataset.numInstances()];
		int[] tempClusterArray = new int[dataset.numInstances()];

        这两个数据并不是类的本身属性，而是方法内部的局部变量，但是因为在操作中比较关键，故专门说明。

        我们预计使用一种简短的，能够快速表示分类情况的存储结构，以方便来比对当前分簇情况与以前的分簇情况是否相同，虽然clusters[][]也可以但是太过于冗杂。于是这里设计了有测试集那么长的一个整型数组，来表示测试集中某行隶属于哪一个类：

         例如，当tempClusterArray[120] = 2，说明数据集的第121行的数据属于第三类簇，你可以在clusters[2]当中找到120。而这里设置tempOldClusterArray 的原因是给上回合的分簇留个备份，便于判断本回合和上回合是否分簇结果一致，从而确定当前结果是否收敛。

三、代码实现过程

1. 距离计算

        相比KNN的计算距离的函数，这里基于KMeans的环境重载了：

        给出的参数paraI表示数据集的某一行，而paraArray是一个四位向量，和数据集的行向量(去掉类)是对应的，因此只需要通过paraI取出数据dataset.instance(paraI)，解析出有效的四维，并求它与paraArray向量的距离即可。

        依旧采用曼哈顿距离和欧式距离两种方案。

	/**
	 *********************
	 * The distance between two instances.
	 * 
	 * @param paraI
	 *            The index of the first instance.
	 * @param paraArray
	 *            The array representing a point in the space.
	 * @return The distance.
	 *********************
	 */
	public double distance(int paraI, double[] paraArray) {
		int resultDistance = 0;
		double tempDifference;
		switch (distanceMeasure) {
		case MANHATTAN:
			for (int i = 0; i < dataset.numAttributes() - 1; i++) {
				tempDifference = dataset.instance(paraI).value(i) - paraArray[i];
				if (tempDifference < 0) {
					resultDistance -= tempDifference;
				} else {
					resultDistance += tempDifference;
				} // Of if
			} // Of for i
			break;

		case EUCLIDEAN:
			for (int i = 0; i < dataset.numAttributes() - 1; i++) {
				tempDifference = dataset.instance(paraI).value(i) - paraArray[i];
				resultDistance += tempDifference * tempDifference;
			} // Of for i
			break;
		default:
			System.out.println("Unsupported distance measure: " + distanceMeasure);
		}// Of switch

		return resultDistance;
	}// Of distance

2. 分簇

		int[] tempOldClusterArray = new int[dataset.numInstances()];
		tempOldClusterArray[0] = -1;
		int[] tempClusterArray = new int[dataset.numInstances()];
		Arrays.fill(tempClusterArray, 0);
		double[][] tempCenters = new double[numClusters][dataset.numAttributes() - 1];

        首先将我们的基础数据结构初始化，这里tempOldClusterArray与tempClusterArray完全不同的初始化是为了避免一开始两者就相等，保证KMeans的结束条件不会一开始就满足，实现循环的顺利进行。

        tempCenter存放的是中心点，因为本代码中k = 3，而且每一个点都是一个4维向量，因此就用3 * 4 的空间来存储3个点集。（tempCenters[0]代表0号簇的中心点、tempCenters[1]代表1号簇的中心点...）

		// Step 1. Initialize centers.
		int[] tempRandomOrders = getRandomIndices(dataset.numInstances());
		for (int i = 0; i < numClusters; i++) {
			for (int j = 0; j < tempCenters[0].length; j++) {
				tempCenters[i][j] = dataset.instance(tempRandomOrders[i]).value(j);
			} // Of for j
		} // Of for i

        第1步，随机分配数据集中的三行作为三个中心点。

        int[] tempClusterLengths = null;
		while (!Arrays.equals(tempOldClusterArray, tempClusterArray)) {
			System.out.println("New loop ...");
			tempOldClusterArray = tempClusterArray;
			tempClusterArray = new int[dataset.numInstances()];

			//...

		} // Of while

        第2步，开始定点与分簇的循环。首先将上回合用剩下的tempClusterArray记录下来，然后给tempClusterArray新的空间开始本轮的再顶点-再分簇。

            // Step 2.1 Minimization. Assign cluster to each instance.
			int tempNearestCenter;
			double tempNearestDistance;
			double tempDistance;

			for (int i = 0; i < dataset.numInstances(); i++) {
				tempNearestCenter = -1;
				tempNearestDistance = Double.MAX_VALUE;

				for (int j = 0; j < numClusters; j++) {
					tempDistance = distance(i, tempCenters[j]);
					if (tempNearestDistance > tempDistance) {
						tempNearestDistance = tempDistance;
						tempNearestCenter = j;
					} // Of if
				} // Of for j
				tempClusterArray[i] = tempNearestCenter;
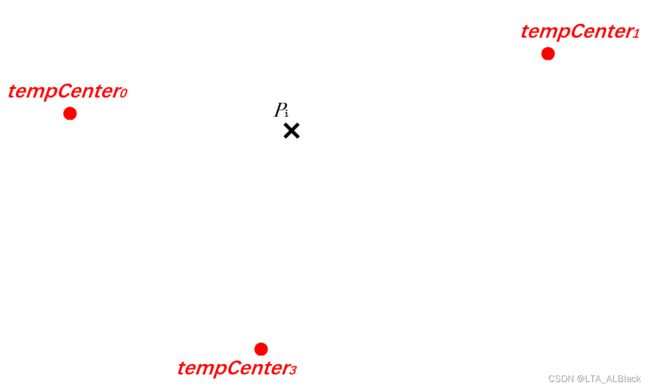
			} // Of for i

        循环内第1步，将每个散点分簇，这个过程可以用下图来描述：

         先定下三（numClusters）个点。

         然后枚举出全部的散点（循环dataset.numInstances()次），上图为某次枚举\(p_i\)

         分别计算出\(p_i\)到三个可能方向的距离

         选择最近的中心点作为\(p_i\)所属簇，并且在变量tempClusterArray[]中记录当\(p_i\)所属簇号：tempClusterArray[i] = tempNearestCenter  若数据集长度为\(N\)，这单次分簇的复杂度为\(O(kN)\)。

			// Step 2.2 Mean. Find new centers.
			tempClusterLengths = new int[numClusters];
			Arrays.fill(tempClusterLengths, 0);
			double[][] tempNewCenters = new double[numClusters][dataset.numAttributes() - 1];
			// Arrays.fill(tempNewCenters, 0);
			for (int i = 0; i < dataset.numInstances(); i++) {
				for (int j = 0; j < tempNewCenters[0].length; j++) {
					tempNewCenters[tempClusterArray[i]][j] += dataset.instance(i).value(j);
				} // Of for j
				tempClusterLengths[tempClusterArray[i]]++;
			} // Of for i

			// Step 2.3 Now average
			for (int i = 0; i < tempNewCenters.length; i++) {
				for (int j = 0; j < tempNewCenters[0].length; j++) {
					tempNewCenters[i][j] /= tempClusterLengths[i];
				} // Of for j
			} // Of for i

        循环内第2、3步，选新的中心点。这里构造的双重循环其实就是遍历数据集的每行，因为要取出逐行的每个属性，因此又套了tempNewCenters[0].length的循环，遮盖写成dataset.numAttributes() - 1也是完全没问题的。

        tempClusterArray可以查询对应数据行被纳入的簇号，因此tempClusterArray[i]就是获得当前循环的第i号行数据对应的簇号，因此tempNewCenters[tempClusterArray[i]]就取得这个簇号对应的中心点四维向量（当前还是空的），然后以j作为变量来遍历从而取得这个四维向量的每个维度，并其中心点附属簇类的散点们进行加和。而tempClusterLengths[tempClusterArray[i]]++;自然就是统计每个簇号所包含的点的个数。这一边进行着加和，一边进行算总数，其本质是为了计算重心：

\[G_x = \frac{\sum_{i=1}^{N} \vec{x_i}}{N}\]

        当然代码中这个描述有一定的越界风险，因为对于某些特大数据，全部加权起来可能有越界风险。因此可以将公式变形为：\[G_x = \sum_{i=1}^{N}\frac{ \vec{x_i}}{N}\]

        因此可以修改原来的代码为：

	double[][] tempNewCenters = new double[numClusters][dataset.numAttributes() - 1];
	// Arrays.fill(tempNewCenters, 0);
	for (int i = 0; i < dataset.numInstances(); i++) {
		for (int j = 0; j < tempNewCenters[0].length; j++) {
			tempNewCenters[tempClusterArray[i]][j] += (dataset.instance(i).value(j)
					/ tempClusterLengths[tempClusterArray[i]]);
		} // Of for j
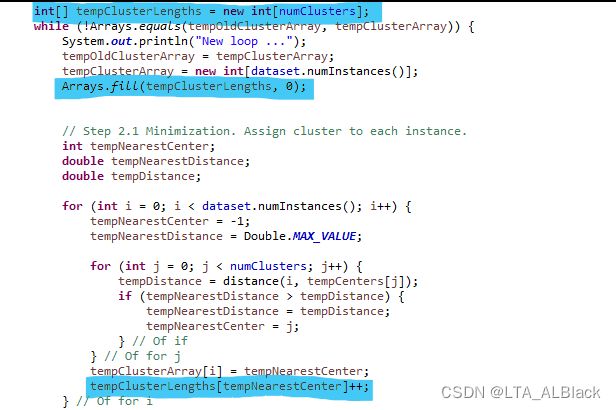
	} // Of for i

        这里tempClusterLengths变量的统计我从原来的选重心的部分放到分簇的代码中了，这样在重心选定的代码中就可以直接拿过来用了，而不用专门用个for循环来统计了。（在分簇部分添加的修改见下图）

         全部代码（第三步是把数据存到clusters里面，是用于打印的，这就不赘述了）：

	/**
	 ******************************* 
	 * Clustering.
	 ******************************* 
	 */
	public void clustering() {
		int[] tempOldClusterArray = new int[dataset.numInstances()];
		tempOldClusterArray[0] = -1;
		int[] tempClusterArray = new int[dataset.numInstances()];
		Arrays.fill(tempClusterArray, 0);
		double[][] tempCenters = new double[numClusters][dataset.numAttributes() - 1];

		// Step 1. Initialize centers.
		int[] tempRandomOrders = getRandomIndices(dataset.numInstances());
		for (int i = 0; i < numClusters; i++) {
			for (int j = 0; j < tempCenters[0].length; j++) {
				tempCenters[i][j] = dataset.instance(tempRandomOrders[i]).value(j);
			} // Of for j
		} // Of for i

		int[] tempClusterLengths = new int[numClusters];
		while (!Arrays.equals(tempOldClusterArray, tempClusterArray)) {
			System.out.println("New loop ...");
			tempOldClusterArray = tempClusterArray;
			tempClusterArray = new int[dataset.numInstances()];
			Arrays.fill(tempClusterLengths, 0);
			

			// Step 2.1 Minimization. Assign cluster to each instance.
			int tempNearestCenter;
			double tempNearestDistance;
			double tempDistance;

			for (int i = 0; i < dataset.numInstances(); i++) {
				tempNearestCenter = -1;
				tempNearestDistance = Double.MAX_VALUE;

				for (int j = 0; j < numClusters; j++) {
					tempDistance = distance(i, tempCenters[j]);
					if (tempNearestDistance > tempDistance) {
						tempNearestDistance = tempDistance;
						tempNearestCenter = j;
					} // Of if
				} // Of for j
				tempClusterArray[i] = tempNearestCenter;
				tempClusterLengths[tempNearestCenter]++;
			} // Of for i


			// Step 2.2 Mean. Find new centers.

			double[][] tempNewCenters = new double[numClusters][dataset.numAttributes() - 1];
			// Arrays.fill(tempNewCenters, 0);
			for (int i = 0; i < dataset.numInstances(); i++) {
				for (int j = 0; j < tempNewCenters[0].length; j++) {
					tempNewCenters[tempClusterArray[i]][j] += (dataset.instance(i).value(j)
							/ tempClusterLengths[tempClusterArray[i]]);
				} // Of for j
			} // Of for i

			System.out.println("Now the new centers are: " + Arrays.deepToString(tempNewCenters));
			tempCenters = tempNewCenters;
		} // Of while

		// Step 3. Form clusters.
		clusters = new int[numClusters][];
		int[] tempCounters = new int[numClusters];
		for (int i = 0; i < numClusters; i++) {
			clusters[i] = new int[tempClusterLengths[i]];
		} // Of for i

		for (int i = 0; i < tempClusterArray.length; i++) {
			clusters[tempClusterArray[i]][tempCounters[tempClusterArray[i]]] = i;
			tempCounters[tempClusterArray[i]]++;
		} // Of for i

		System.out.println("The clusters are: " + Arrays.deepToString(clusters));
	}// Of clustering

四、数据测试与进行外部评价

        测试代码：

	/**
	 ******************************* 
	 * Clustering.
	 ******************************* 
	 */
	public static void testClustering() {
		KMeans tempKMeans = new KMeans("D:/Java DataSet/iris.arff");
		tempKMeans.setNumClusters(3);
		tempKMeans.clustering();
	}// Of testClustering

	/**
	 ************************* 
	 * A testing method.
	 ************************* 
	 */
	public static void main(String arags[]) {
		testClustering();
	}// Of main

        结果：

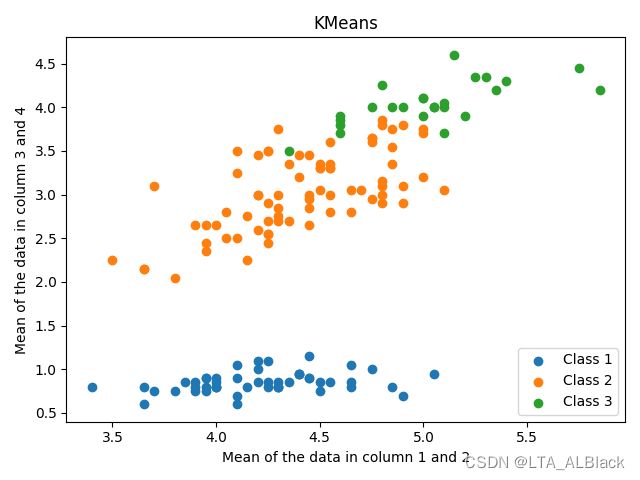
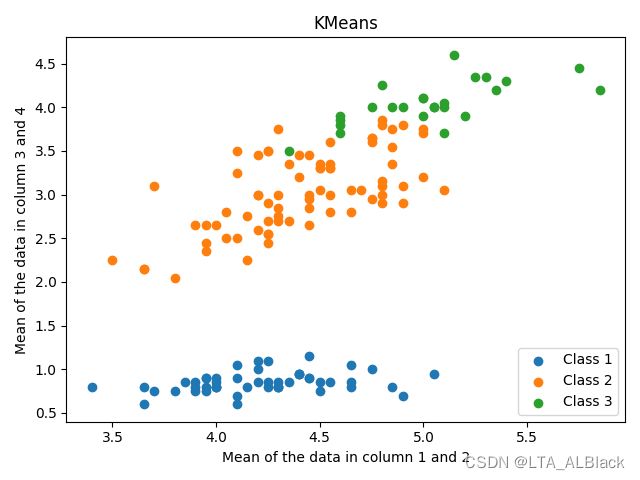
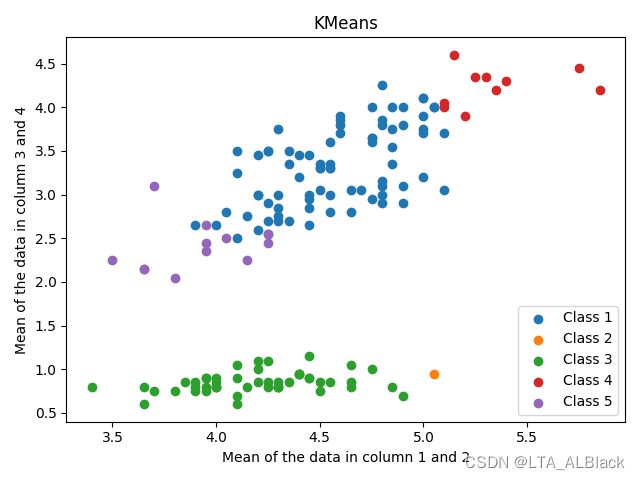
        怎么说呢，这个结果并不是非常直观，于是我试着对结果部分进行归一化，将数据集的第一列与第二列求平均以作为横坐标，第三列与第四列求平均以作为纵坐标，可得下面的散点图： 

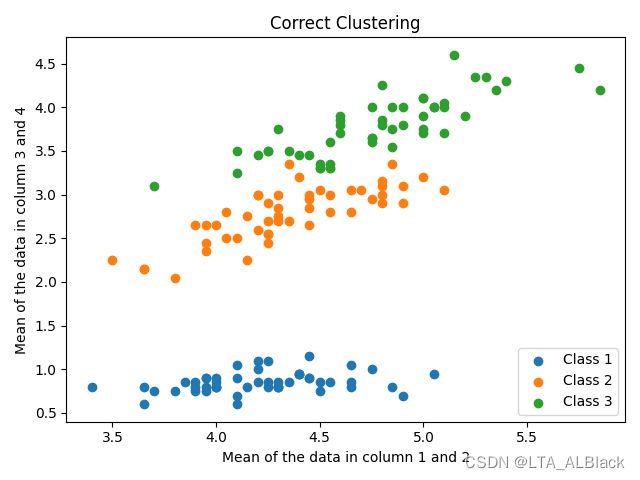
        然后通过遍历数据集，带入已知的类别属性，我们可以得到正确的聚类情况（进行外部评价）：

        可以发现，第一类数据因为远离上方的数据集，因此与上方数据的数据间耦合性不强，可以较好地分簇，而第二类与第三类因为聚集与上方，故难以区分，也是聚类最不稳定的地方。

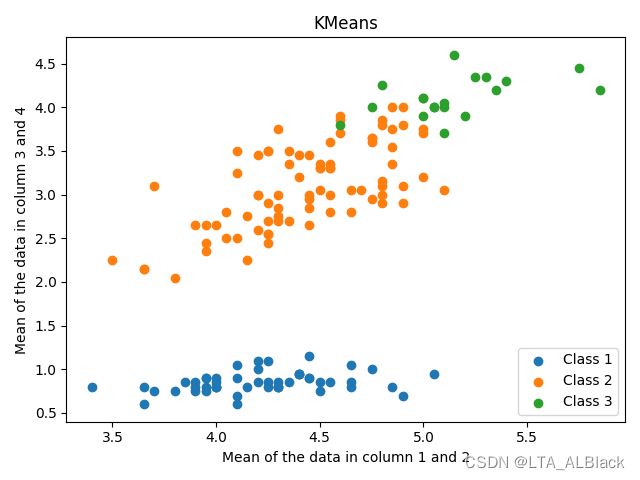
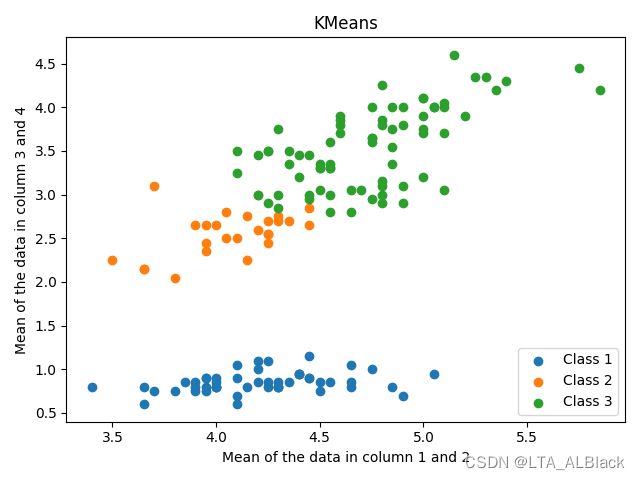
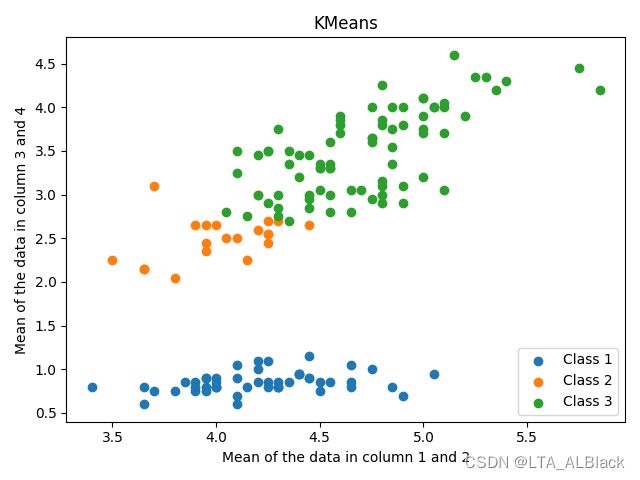
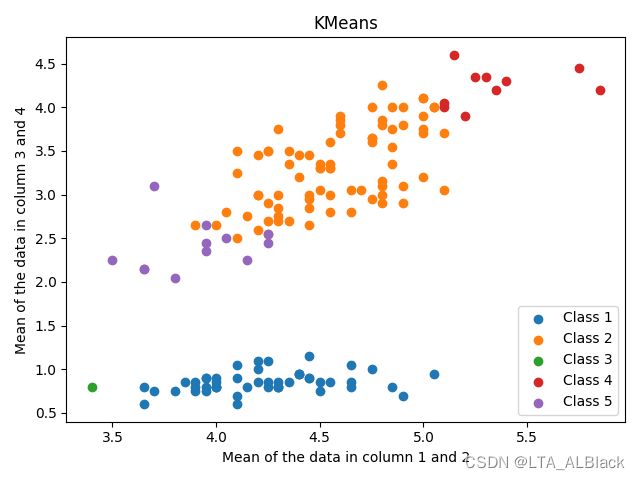
        因为初始点的选取是随机生成，所以为了具体体现随机性初始点对于KMeans的影响，我们不妨再多次运行下KMeans算法，查看散点图的分布情况：

        不同的初始点选择直接导致了最终聚类时第二类与第三类的不稳定，要么第二类多一些，要么第三类多一些。

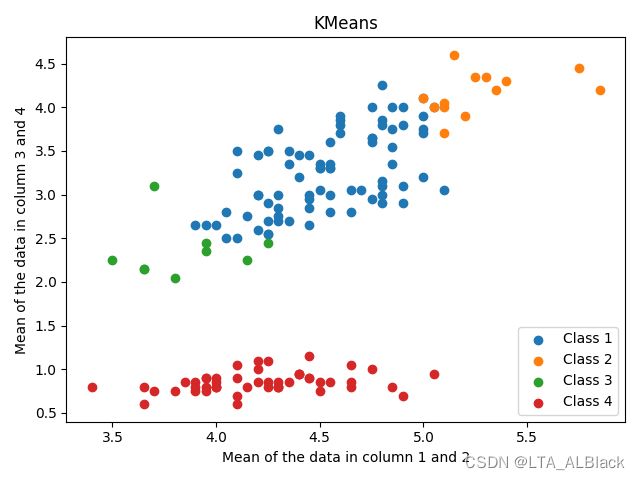
        但是不妨尝试一个想法，当k不再是3，即说KMeans的估计k值与正确的分类数目出现偏差时，我们会得到一个什么样的结果呢？（下图的类与实际类别无关）

 

        可以发现随着k的增加，其实很多簇已经变得不可靠了，我尝试了更大的k，发现大多数有数据的簇最多就4个或者3个，其余簇几乎没有数据。基本上k在2、3、4就是稳定状态，当k再增大其实有数据簇个数就不变了，也许这是数据量过小的原因，据老师所说，在数据量足够大的时候，K值变对于结果的影响会更明显。

· 关于聚类的评价指标

        综上分析，合理选择KMeans的k的确是个难题，也是一个关键问题。

        于是就有人提出了关于聚类的一些评价指标，其实分类是比较好确定指标的，只要有原本的类别，那么可以通过比较来实现，比如kNN，但是聚类并不容易。我上面这些比较是因为我们刚好有这个数据集真实的数据类别，所以可以通过比较的方法来判定好不好，但是真实的聚类是完全不知道真实的类别是什么样的，不可能有上述站在上帝模式下分析数据（这种角度下评价数据的被称之为进行外部评价）。而一般来说，我们可以同一些指标来判断簇内是否有很好的内聚性，簇之间是否有足够低的耦合性，若能达到这种要求，那么这种聚类就是不错的。

（补充的57天内容）扩充的中心点查找策略

        今天因为进行了毕业论文答辩，时间耽误得有点多，于是完成了一些比较简单的内容。

        任务很简单，扩充设计了一个中心点的查找策略即可。昨日是根据簇内的所有点来确定一个重心点作为新的簇内中心点，但是这个中心点可能是个虚点，即这个计算出的点可能不属于任何一个数据集中的数据。

        今日代码将在获得虚拟中心后，换成与其最近的点作为实际中心，再聚类：

	// Step 2.3 Mean. Get new actual centers.
	for (int i = 0; i < numClusters; i++) {
		tempNearestCenter = -1;
		tempNearestDistance = Double.MAX_VALUE;
		for (int j = 0; j < dataset.numInstances(); j++) {
			tempDistance = distance(j, tempCenters[i]);
			if (tempNearestDistance > tempDistance) {
				tempNearestDistance = tempDistance;
				tempNearestCenter = j;
			} // Of if
		} // Of for j
		tempCenters[i][0] = dataset.instance(tempNearestCenter).value(0);
		tempCenters[i][1] = dataset.instance(tempNearestCenter).value(1);
		tempCenters[i][2] = dataset.instance(tempNearestCenter).value(2);
		tempCenters[i][3] = dataset.instance(tempNearestCenter).value(3);
	} // Of for i

        基本上下文解释：

• tempCenters是循环体中的工具遍历，用于表示当前的中心点。这里在使用tempCenters时，其内部已经存放了所有簇的重心
• 循环体中取出了全部可能的点，使用distance函数计算它们彼此的距离

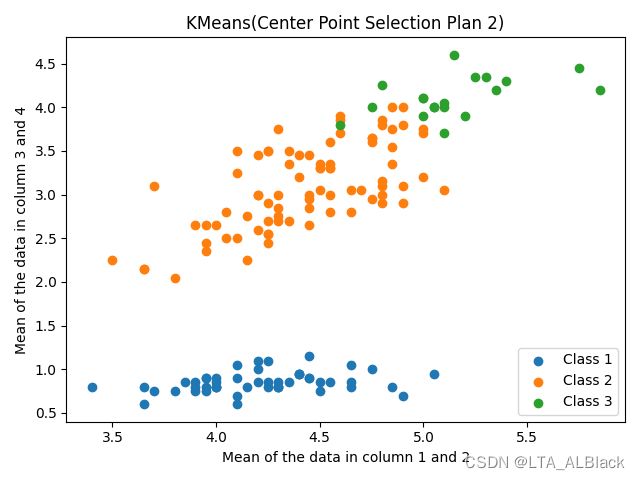
        测试效果：

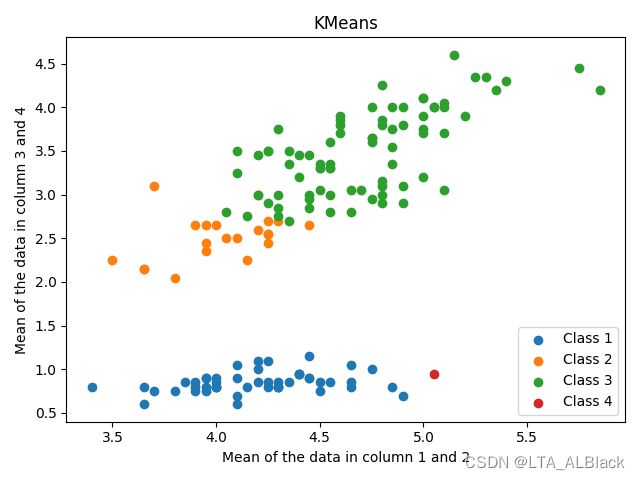
         此外，在本轮测试中发现了一个特殊的失败案例：

         这个案例很有意思，我们最初随机生成的中心点可能过于偏向左下，导致最后确定的实点稳定在左下方。在分簇的时候这个点集似乎很惨，多次调整后没有分到一个数据（也许曾经分到了，最后撤销了也说不定）

        但是这样的数据真的是失败吗？其实上面绿色的数据作为一整类，下面作为橙色数据作为一类也不是不可以，至少从视觉上来看，绿色与橙色的耦合性是很低的，内聚性比较明显，若不是预先知道数据有三类，设置k = 2的话似乎是给人感觉最佳的值呢。所以KMeans的k选择真的让人头疼呀╮(╯▽╰)╭