各种最短路问题的常用算法模板

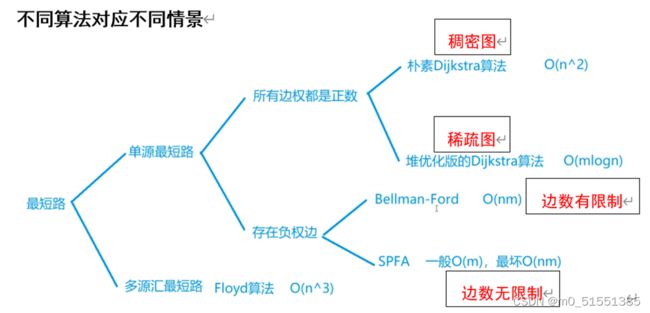
1、所有最短路算法

2、最短路问题的关键

实际做题时的关键是如何定义点和边，使问题变成最短路问题。

3、边权都>0的最短路

3.1 朴素版dijkstra算法

不能有负权边。

#include
#include
#include

using namespace std;

const int N = 510;

int n, m;
int g[N][N];
int dist[N];
int st[N];

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    for (int i = 0; i < n; i++)
    {
        int t = -1;
        for (int j = 1; j <= n; j++)
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        
        st[t] = true;
        
        for (int j = 1; j <= n; j++)
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    
    if (dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}

int main()
{
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);
    
    while (m--)
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c);
    }
    
    cout << dijkstra();
    
    return 0;
}

3.2 堆优化版dijkstra算法

就是用优先队列优化了 “寻找当前未确定最短距离的点中到源点距离最短” 的过程，原来寻找是遍历n个点，用O(n)的时间。现在只需O(1)的时间即可找到。

#include
#include
#include
#include

using namespace std;

const int N = 1e6 + 10;

typedef pair<int, int> PII;     // 存储一个节点的编号，及其到源点的最短距离

int n, m;
int h[N], e[N], ne[N], w[N], idx;
int dist[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    w[idx] = c;
    idx++;
}

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, 1});
    
    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();
        
        int ver = t.second, distance = t.first;
        if (st[ver]) continue;
        st[ver] = true;
        
        for (int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > distance + w[i])
            {
                dist[j] = distance + w[i];
                heap.push({dist[j], j});
            }
        }
    }
    
    if (dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    
    while (m--)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    
    cout << dijkstra() << endl;
    
    return 0;
}

4、有负权边的最短路

如果有负权回路，最短路不一定存在。

转无穷多圈

4.1 对边的数量有限制：Bellman-Ford算法

Bellman-ford算法可以检测负环，但是一般不用它检测。

#include
#include
#include

using namespace std;

const int N = 510, M = 10010;

int dist[N];
int backup[N];
int n, m, k;

struct Edge
{
    int a, b, w;
}edges[M];

bool bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    for (int i = 0; i < k; i++)
    {
        memcpy(backup, dist, sizeof dist);
        for (int j = 0; j < m; j++)
        {
            int a = edges[j].a;
            int b = edges[j].b;
            int w = edges[j].w;
            dist[b] = min(dist[b], backup[a] + w);
        }
    }
    
    if (dist[n] > 0x3f3f3f3f / 2) return false;
    else return true;
}

int main()
{
    cin >> n >> m >> k;
    for (int i = 0; i < m; i++)
    {
        int a, b, w;
        cin >> a >> b >> w;
        edges[i] = {a, b, w};
    }
    
    int t = bellman_ford();
    
    if (!t) cout << "impossible" << endl;
    else cout << dist[n] << endl;
    
    return 0;
}

思考：

拷贝dist数组的目的是 保证每次更新所有边的最短路时，都是用上一次 只扩展了一条边得到的dist，防止在遍历所有边时发生串联更新。

注意：

更新dist的时候使用的下标是哪个？使用的数组又是哪个？？这两块在写代码的时候很容易错。

4.2 对变数无限制 PSFA算法

本算法非常的常用，正权图也能用。
只要没有负环，就能用该算法。

#include
#include
#include
#include

using namespace std;

const int N = 1e5 + 10;

int dist[N];
int e[N], ne[N], h[N], idx, w[N];
bool st[N];
int n, m;

void add(int a, int b, int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx;
    idx++;
}

bool spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    queue<int> q;
    q.push(1);
    st[1] = true;
    
    while (q.size())
    {
        auto t = q.front();
        q.pop();
        
        st[t] = false;
        
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > w[i] + dist[t])
            {
                dist[j] = w[i] + dist[t];
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    
    if (dist[n] > 0x3f3f3f3f / 2) return false;
    else return true;
}

int main()
{
    cin >> n >> m;
    
    memset(h, -1, sizeof h);
    
    while (m--)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    
    int t = spfa();
    
    if (!t) cout << "impossible" << endl;
    else cout << dist[n] << endl;
    
    return 0;
}

思考：

为什么bellmam-ford算法最后判断时写成 if(dist[n] > 0x3f3f3f3f / 2) 而spfa算法写成 if(dist[n] == 0x3f3f3f3f) ？？
答：
对于bellman-ford算法： dist[n] = 0x3f3f3f3f 表示起点到中间没有通路，但可能有其他的点和终点是连着的。而bellman-ford算法会遍历图中的所有边，所以，如果终点有边连着（但起点到不了终点），终点的dist[n]会被更新为0x3f3f3f3f + 边权，这个值会比0x3f3f3f3f小一点点，所以判断的时候不能判断 == 。

对于spfa算法：spfa只会遍历由起点能更新到的点，起点到不了的点根本不会更新，所以，如果起点到不了重点的话，终点的dist根本不会更新，所以直接判断 == 即可。

注意：

spfa是bellman-ford算法的优化，后者傻傻的遍历图中的所有边，而spfa只会遍历可由起点更新到的点。

4.3 用 spfa 算法判断图中 是否有负环

#include
#include
#include
#include

using namespace std;

const int N = 1e5 + 10;

int dist[N], cnt[N];
int e[N], ne[N], h[N], idx, w[N];
bool st[N];
int n, m;

void add(int a, int b, int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx;
    idx++;
}

bool spfa()
{
    queue<int> q;
    
    for (int i = 1; i <= n; i++)
    {
        q.push(i);
        st[i] = true;
    }
    
    while (q.size())
    {
        auto t = q.front();
        q.pop();
        
        st[t] = false;
        
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > w[i] + dist[t])
            {
                dist[j] = w[i] + dist[t];
                cnt[j] = cnt[t] + 1;
                if (cnt[j] >= n) return true;
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    
    return false;
}

int main()
{
    cin >> n >> m;
    
    memset(h, -1, sizeof h);
    
    while (m--)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    
    int t = spfa();
    
    if (t) cout << "Yes" << endl;
    else cout << "No" << endl;
    
    return 0;
}

思考①：

1、为什么不需要初始化dist数组为+∞？这样不会对后面更新dist产生影响吗？？
2、为什么开始时所有点都要入队？
答：
这两个问题可以一起理解。我们在原图的基础上加入一个虚拟源点，单向指向所有节点且到所有点距离为0。开始时，初始化dist为+∞，并将虚拟源点加入队列中，然后进行spfa算法的第一次迭代。由于虚拟源点到每个点都有边，所以所有点的dist都会更新为0，并将所有点插入队列中，此时就等价于上面的spfa算法了。

开始将所有点入队的根本原因是 处理不连通的情况。即，负环和起点是不连着的，所以只通过起点根本无法遍历到负环，所以要将所有点入队。无向连通图不需要建虚拟源点了，有向图除非强连通，否则不能保证从1号点能到达其他所有点， 也应建立虚拟源点。
如果只是求源点可以到达的负环的话，只将源点入队即可。

从另外一个角度理解不初始化dist数组。如果图中存在负环，则dist一定会更新无穷次，所以不初始化dist也没关系。这样看来，不管dist数组的初值是多少，都是可以的。因为只要有负环存在，就必然有某些点的距离是负无穷，所以不管距离被初始化成何值，都一定严格大于负无穷，所以一定会被无限更新。

思考②：

dist全初始化为0后，只有负权边才会使dist变小，所以cnt从第一次出现负权边时开始统计，他统计了该负权边延伸的最大长度，当负环第一次出现时，cnt等于负环上的节点数，该节点数小于等于n，之后cnt会一直增加到-∞，但我们的代码不会让他增长到-∞，此处只需给出最小的判环结束条件即可，无负环最极限的条件是存在 cnt == n - 1 ，即cnt >= n时一定存在负环。

5、多源汇最短路———Floyd算法

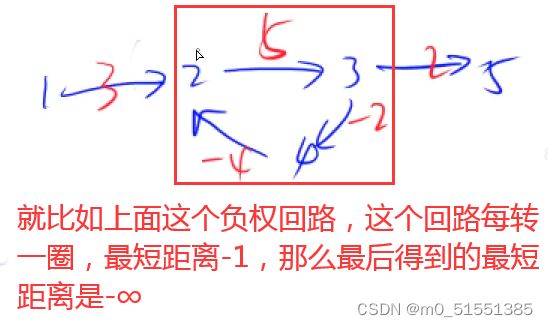
可以处理有负权边的图，但是不能有负权回路

#include
#include
#include

using namespace std;

const int N = 210, INF = 1e9;

int d[N][N];
int n, m, query;

void floyd()
{
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main()
{
    cin >> n >> m >> query;
    
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            if (i == j) d[i][j] = 0;
            else d[i][j] = INF;
    
    while (m--)
    {
        int a, b, w;
        cin >> a >> b >> w;
        d[a][b] = min(d[a][b], w);
    }
    
    floyd();
    
    while (query--)
    {
        int a, b;
        cin >> a >> b;
        
        if (d[a][b] > INF / 2) cout << "impossible" << endl;
        else cout << d[a][b] << endl;
    }
    
    return 0;
}