【C语言】八大排序算法,速收藏这篇2w字详解
前言
如果你把本专栏从头看到这里,那么恭喜你,本篇博客已经是是初阶数据结构的收尾啦!让我们一起来学习一下,那些常见的排序算法!
本篇博客主要讲述八大排序️♀️,桶排序/基数排序可能会在后期补上
我的个人博客已经搭建!这是本文在个人博客的链接传送门
在之前的学习中,我们已经接触过ez的冒泡排序,和通过堆实现的堆排序,本篇博客就不再详解这两个了!
有些排序的思路不是那么好懂,我的讲解也会有不到位的地方,欢迎在评论区提出你的疑惑或建议!
文章目录
- 前言
- 1.插入排序
-
- 1.1直接插入
- 1.2希尔排序
- 2.选择排序
-
- 2.1直接选择
- 2.2堆排序
- 3.交换排序
-
- 3.1咕噜咕噜排序
- 3.2快速排序
-
- 3.2.1 Hoare法
-
- 两种极端情况
- 3.2.2 挖坑法
- 3.2.3 前后指针法
-
- 优化极端情况
- 3.2.4快排的时间/空间复杂度
- 3.3快排非递归实现
- 4.归并排序
-
- 4.1打印printf调试大法
- 4.2递归源码
- 4.3非递归实现
-
- 4.3.1 条件断点
- 4.4归并排序的时间/空间复杂度
- 5.计数排序
-
- 5.1计数排序的特性
- 6.排序算法的稳定性
-
- 6.1稳定性表格
- 7.利用clock函数查看排序耗时
- 结语
1.插入排序
1.1直接插入
基本思想:把待排序的数依照大小插入一个已经有序的序列中,直到所有数插入完毕,就能得到一个新的有序序列
实际上我们日常生活中打斗地主,在码牌的时候就运用了这种思想。把相同的数放在一起,并依照从小到大排列
你可能会疑惑,都“已经有序”了,那还怎么排序?
- 这需要我们之前学习链式二叉树时接触到的分治思想
- 当我们手头上只有两个数的时候,将大的那个数插入到小的数后头,就形成了一个有序的2数序列
- 这时候再让下一个数加入进来,把它插入到相应位置,得到一个有序的3数序列
- 依次递进,最终就能得到一个有序的N数序列
如果学习过分治思想的你,肯定一拍桌子道:“我知道了,手头上只有两个数的时候,就是分治的末端条件!”
没错,我们就是要利用这种思想,实现从两个数开始的插入排序!
给定一个数组,需要你使用插入排序,将它变成升序序列
我们就从9开始,将1插入到9的前面,2插入到1、9之间,……
这样就能最终排序出1 2 3 4 5 5 6 7 8 9的结果
最后以代码的形式操作,如下面所示
// 插入排序
void InsertSort(int* a, int n)
{
//在一个数组中插入新的数,每一趟都让最后的end+1的数据大于end
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = a[end+1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
break;
}
a[end+1] = tmp;
//最后end不符合条件出循环的时候,end可能为-1,a[end]会越界
//如果是break出的循环,end+1和tmp的位置相同,自己等于自己,问题不大
}
}
由此我们可以总结出直接插入排序的一些特性
- 时间复杂度:O(N2)
- 空间复杂度:O(1),是原地算法
- 元素越接近有序的时候,需要交换的次数就越少,算法的效率越高
1.2希尔排序
希尔排序是对直接插入的优化,又称“缩小增量法”。之前我们是进数组之后直接开R,现在先Q一下再R闪,这样才能打出更秀的操作。不过我的盲僧很菜,R闪就没有成功过
喂喂喂,好像跑题了!
基本思想:先选定一个整数gap,让后把待排序数据以gap为间隔进行单独的插入排序(预排序),这样让数列做到局部有序,最后在进行插入排序,达到优化插入排序算法效率的目的
比如我们设定gap=3,这样原本的数组就被分割成了下面的模样,接着我们先对这3组数据进行单独的插入排序【这个操作被称为 预排序】
你能写出它们单独插入排序后的结果吗?
这时候我们的序列虽然不是有序的,但是只看一个小局部的时候,它是有序的。
这样能减少插入排序操作时候的比较次数,自然效率就变高了
执行完预排序后,我们就可以对现在的新序列进行插入排序了。但是直接这么调用还不够优化。
再仔细看看上面的思路,你会发现,其实gap=1的时候,就相当于一次插入排序了
- 而且当数据量很大的时候,我们也需要实时改变我们的
gap。 - 待排序数据有100个,gap=3就太小了,优化了个寂寞。
- 待排序数据有10个,gap=20就是搬起石头砸自己的脚,同样不行!
解决这个方法其实很简单,我们只需要根据待排序数据的大小动态设置gap就可以了,比如gap=n/2
这时候就可以进行这么一个操作:每次预排序过后就改变一下gap,直到最后gap=1执行一次插入排序,数列有序
落实到代码上,我们只需要把插入排序中所有和1有关的操作都改成gap,就实现了希尔排序
- 这里需要注意的是gap的范围,因为我设置的是gap每次都/3,所以在最后可能会出现
gap=2/3=0的情况,这时候其实排序还没有结束,但已经跳出循环了。我们需要在末尾+1保证最后一次插入排序的gap=1
// 希尔排序
void ShellSort(int* a, int n)
{
//只要把插入排序中的1全部改成grap,就能形成一次间隔为3的预排序
//当grap=1时,效果同插入排序相同
int grap = n;
while (grap > 1)//当grap=1,说明上一把已经是插入排序了
{
grap=grap/3+1;//每一次都/3,再+1防止grap=2/3的情况
for (int i = 0; i < n - grap; i++)
{
int end = i;
int tmp = a[end + grap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + grap] = a[end];
end -= grap;
}
else
break;
}
a[end + grap] = tmp;
}
}
}
希尔排序的时间复杂度不好确定,因为我们通常会选取不同的gap,导致时间效率也不同。不过大部分资料中给出的时间复杂度如下
O ( N 1.25 ) 到 O ( 1.6 ∗ N 1.25 ) O(N^{1.25})到O(1.6*N^{1.25}) O(N1.25)到O(1.6∗N1.25)
在“菜鸟教程”网,有对希尔排序时间复杂度的解析传送门
2.选择排序
2.1直接选择
基本思路:遍历一遍数组,从中找出最大或最小的那一个数,然后将其放在数组前端。下一次遍历的时候,不再遍历这个数。
注意:得到最大最小值后,需要将其和数组开头(或者结尾)的数进行交换,而不能直接覆盖,不然会出现数据丢失
这个排序的思路非常好理解。进一步拓展,如果我一次遍历选出两个数,将最大值放在数组尾部,最小值放在数组开头,就可以减少一半遍历的次数。
// 数据交换
void Swap(int* a, int* b){
int tmp = *a;
*a = *b;
*b = tmp;
}
// 直接选择排序
void SelectSort(int* a, int n)
{
int max ,min;
int left = 0, right = n - 1;
while (left < right){
max = min = left;//存放下标便于后面的交换
for (int i = left; i <= right; i++)
{
if (a[i] >=a[max]){
max= i;
}
if (a[i] <= a[min]){
min= i;
}
}
Swap(&a[min], &a[left]);
if (max == left) {
max = min;
}//如果max数据在开头,第一次交换会被替换
//所以需要重定向max的位置,再交换max
Swap(&a[max], &a[right]);
left++;
right--;
}
}
不过,这个算法需要多次遍历数组,效率自然低的离谱,堪比冒泡(甚至比冒泡还拉)
- 时间复杂度:O(N2)
- 空间复杂度:O(1)
2.2堆排序
堆排序是指利用二叉树-堆这种数据结构来进行选择数据的一种排序算法,它是选择排序的一种。
需要注意的是:升序要建大堆,排降序建小堆
堆排序已经在之前的博客中讲解过,点击下方连接即可查看!
【C语言】什么是堆?堆排序和TopK问题又是如何实现的
这里给出堆排序的源码,或许聪明的你看源码就能看懂呢?
// 堆排序
void AdjustDown(int* a, int n, int root)
{
assert(a);
int parent = root;
int child = parent * 2 + 1;//左孩子
while (child < n){
//找左右孩子中小的那一个
if (child + 1 < n && a[child] < a[child + 1])
{//如果左孩子大于右孩子,则选择右孩子
child++;
}
if (a[child] > a[parent]){
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else{
return;
}
}
}
// 升序用大堆
// 降序用小堆
void HeapSort(int* a, int n)
{
// 向下调整--建堆 O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i){
AdjustDown(a, n, i);//此时建的是一个小堆
}
PrintArray(a, n);
size_t end = n - 1;
while (end > 0){
Swap(&a[0], &a[end]);//前后交换,最大的数放到末尾,不进行下一次调整
AdjustDown(a, end, 0);
end--;
}
}
3.交换排序
3.1咕噜咕噜排序
说道冒泡排序啊,那就是陪伴咱们C语言学习始终的一个老朋友了。
在C语言进阶的学习中,我曾写过一篇博客,里面讲解了用冒泡来模拟实现库函数qsort传送门
它的思路就是对两个数进行比较,较大的数往尾部移动,较小的数字往头部移动
在very very long time ago,我也写过关于冒泡排序的博客
初识C语言==>冒泡排序
// 冒泡排序
void BubbleSort(int* a, int n)
{
for (int i = 0; i < n; i++)
{
int exchange = 0;
for(int j=0;j<n-1-i;j++)
{
if (a[j] > a[j + 1]){
exchange=1;
Swap(&a[j], &a[j + 1]);
}
}
if (exchange == 0){
break;
//如果单趟排序没有发生交换,说明此时已经有序
}
}
}
- 空间复杂度:O(N2)
- 时间复杂度:O(1)
3.2快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序算法。
基本思想:任取待排序序列中的某个元素作为基准值,按照该基准值将待排序集合分割成两个子序列,左子序列中所有元素均小于基准值,右 子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
3.2.1 Hoare法
发明快排的大佬给出了一个方法,假设0下标处为基准值key。用左右指针来遍历数组,右指针找到比key小的数后停下,左指针找找到比key大的数后停下,它们俩进行交换。
最后left和right相遇的时候,左右序列就已经排好了,此时将key与它们相遇的位置进行交换。新的序列key的左边小于key,右边大于key(此时不一定有序)
- 疑问:既然最后要将相遇位置和key进行交换,那要怎么保证相遇位置小于key?
- 答:通过右指针先走来实现!
可能说完思路后,你还是不太了解这左右指针是怎么走的,别着急,来康康我画的动图
因为是右指针先走,所以右指针停下的位置,一定是小于key的位置。此时只会是L来交R,不可能是R往左遇到L(因为L停下的位置大于key,在此右边不可能没有一个小于key的值)
比如下图所示,如果L的位置右边只有一个比key小的值,那R在第一趟就会来到2的位置,然后L向右走一步与R相交,直接交换
两种极端情况
也会有下面的两种极端情况
- key右侧没有比key小的值,那么R会直接与L相交,再原地交换key
- key右侧没有比key大的值,R先移动(原地不动),L直接与R在末尾相交,前后交换
这两种极端情况,就是快排的弱势所在,在后头会讲述如何优化key的选则,来避免这种极端情况
下面给出hoare法的代码,中间的代码是一趟hoare排序的实现,而在末尾,我们递归排序key的前半区域和后半区域,一直递归到最小区间:【区间只有一个值,或者区间不存在】
void QuickSort1(int* a, int begin, int end)//hoare
{
if (begin >= end){
return ;//分治的末端条件判断
}
//一趟排序
int left = begin, right = end;
int keyi = begin;
while (left < right)
{
while ((a[right] > a[keyi])&&(right>=begin))
{
right--;
}
while ((a[left] <= a[keyi])&&(left<right))
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left],&a[keyi]);
keyi = left;//必须移动keyi的位置
//递归排序左右区间
QuickSort1(a, begin, keyi-1);
QuickSort1(a, keyi + 1, end);
}
3.2.2 挖坑法
挖坑法的思路比Hoare更好理解,详情见动图
我们先用一个变量保存key的值(不是保存下标),然后R先走找比key小的,与坑位交换,L找比key大的,与坑位交换。最终LR相遇的时候,把key放回相遇位置,就完成了一趟排序
注意:图中为了便于理解,将坑位用空白表示。实际在内存中操作的时候,坑位可以一直是key的值,不需要真的把它移走或者删除
怎样?是不是比方法1好理解一些呢?
下面给出挖坑法的代码示例
//挖坑
void QuickSort2(int* a, int begin, int end)
{
if (begin >= end) {
return;
}
int left = begin, right = end;
int keyi = a[begin];//先存放keyi的值
int pit = begin;//pit作为坑位
while (left < right)
{
while ((a[right] > keyi) && (right >= begin))
{
right--;
}
Swap(&a[pit], &a[right]);
pit = right;
while ((a[left] <= keyi) && (left < right))
{
left++;
}
Swap(&a[pit], &a[left]);
pit = left;
}
QuickSort2(a, begin, pit - 1);
QuickSort2(a, pit + 1, end);
}
3.2.3 前后指针法
这部分就不画动图了,不知下面的这种方式能不能讲解清楚呢?
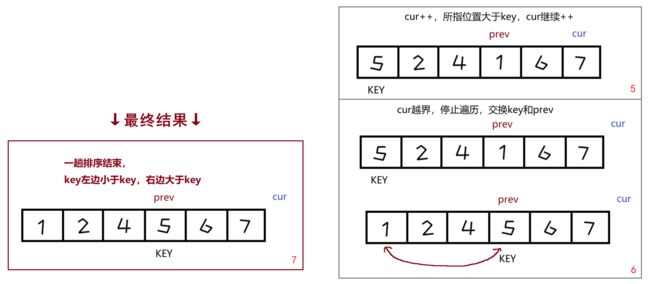
这里需要弄明白的是cur和prev是分别在什么情况下移动
- cur比key小的时候,prev往后++一位,二者交换(在刚开始的时候是原地交换,但在图4中就不是原地交换了)
- cur比key大的时候,prev不动,cur继续往后++,直到找到比key小的数或者越界后停止(如果找到比key小的,就执行上一步的交换)
- 最终cur越界了,交换prev和key的数据,一趟排序完成
下面给出前后指针法的代码示例
void QuickSort3(int* a, int begin, int end)//前后指针
{
if (begin >= end) {
return;
}
int keyi = begin;
int prev = begin, cur = begin + 1;
while (cur <= end)
{
while ((a[cur] < a[keyi]) && (a[++prev] != a[cur]))
{
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
QuickSort3(a, begin, keyi - 1);
QuickSort3(a, keyi + 1, end);
}
优化极端情况
上面提到了快速排序有两种极端情况,我们可以用一个操作来优化它:
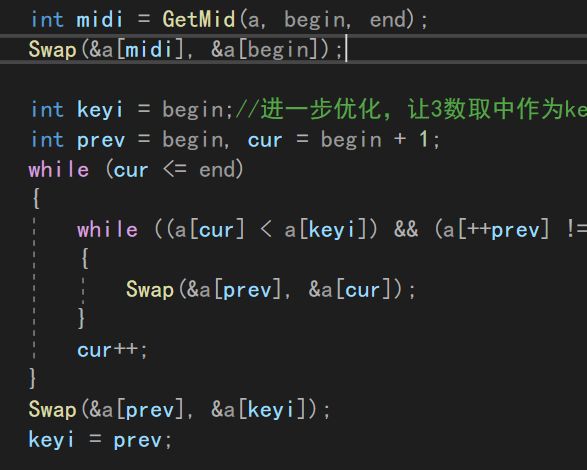
既然key取数组首或尾部都可能会遇到它的后面没有比它小(或大)的数,那我们就让key尽量作为数组有序后应该处于中部的数来作为key
这时候不能直接选取待排序数组中部的数,因为它不一定是数值正好的那个
我们可以选取数组开头、末尾、中间的3个数进行比较,再选择这3个数里面居中的那个数作为我们的key,这样就能避免无效遍历!
int GetMid(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right]){
return mid;
}
else if (a[left] > a[right]){
return left;
}
else{
return right;
}
}
else // a[left] > a[mid]
{
if (a[mid] > a[right]){
return mid;
}
else if (a[left] < a[right]){
return left;
}
else{
return right;
}
}
return -1;//其实这个没啥意义
}
但是单纯加上这个代码并不可行,因为这时候的key不再处于序列开头了,也就意味这我们后头的代码都需要重新写一遍!
这不坑爹吗这是?!
为了不没事找事重写一遍代码,这里直接把找到的MID和left进行交换就OK了!
同时,为了避免多次递归导致栈溢出,我们还可以设置一个条件,在序列长度小于10的时候调用其他排序(比如插入排序)来实现后面的排序操作
3.2.4快排的时间/空间复杂度
快排的递归调用非常类似链式二叉树的前序遍历,它一共会递归logN层级,每一层加起来都有N个数,这样就能算出它的时间复杂度
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN),这个是递归开辟栈帧的空间消耗
3.3快排非递归实现
这部分的知识就比较深奥了,你可以先看看这篇博客,了解一下函数调用的时候会发生什么传送门
但不要担心,其实它的思路并没有那么难!
首先需要先搞明白,递归调用的本质是在操作什么?
在快排中,递归调用的本质是让程序自己来缩小排序的范围,再逐步扩大
那我们可不可以利用数据结构中的栈,来模拟实现程序运行中的递归操作呢?
- 排序完一趟后,将下一趟的左右范围入栈
- 程序先调用存放在栈顶的右边范围进行排序,并把这个范围的左右小区间再次入栈
- 最后右边的区间已经不可再分,就开始返回调用左边区间
这个操作就犹如链式二叉树的后序遍历,先递归访问右节点,再往回返回左节点
最后得到的结果就是类似递归调用完毕后的结果
如果你还没有学习数据结构里面的栈,点我速览!
下面给出一个非递归的实现:
// 非递归
void QuickSort4(int* a, int begin, int end)
{
Stack st;
StackInit(&st);
StackPush(&st, begin);
StackPush(&st, end);
while (!StackEmpty(&st))
{
int right = StackTop(&st);
StackPop(&st);
int left = StackTop(&st);
StackPop(&st);
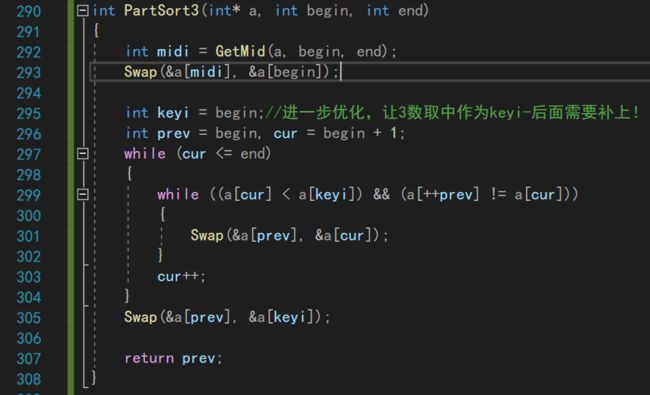
int keyi = PartSort3(a, left, right);
// [left,keyi-1][keyi+1,right]
if (left < keyi-1)
{
StackPush(&st, left);
StackPush(&st, keyi-1);
}
if (keyi + 1 < right)
{
StackPush(&st, keyi+1);
StackPush(&st, right);
}
}
StackDestory(&st);
}
注意:因为这里需要得到一趟递归调用后返回的keyi,所以我们需要把之前写的一趟快排单独拿出来,并设置返回值
来调用一下试试,成功了!
4.归并排序
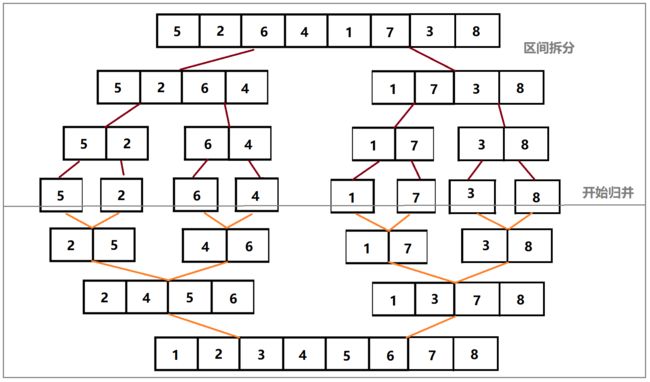
基本思想:采用分治递归,将已有的子序列合并,得到一个有序的序列。即先使每个子序列有序,再使子序列段间有序
- 若将两个有序表合并成一个有序表,称为二路归并
实现的步骤如下图
- 先将区间通过递归分割成分治末端(只有一个值)
- 再对相邻两个区间进行比较,开辟一个新的数组,依次将两个区间中小的那个按顺序摆放在新的数组中,再拷贝回原数组,就实现了归并
- 当区间不存在的时候,开始返回递归,直到序列有序
4.1打印printf调试大法
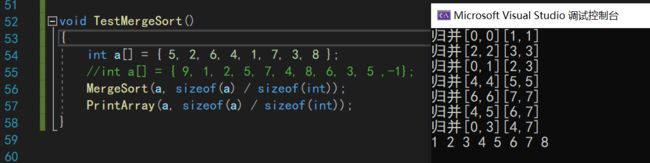
这里最需要注意的就是分治的序列区间问题,如果代码不对,就很容易形成越界访问!
这里我们可以通过printf调试大法来实现,打印出每一层递归时的区间,就能发现可能存在的越界访问问题。这种方法还能帮助我们理解分治递归
printf("[%d,%d][%d,%d]\n", begin, mid, mid+1, end);
如果你在写程序的时候,发现控制台的光标闪动了很久都没有打印出数据,那么多半是程序中有死循环和bug
比如现在,我们初步查看递归调用中是没有出现越界的,但是答案错误,进一步调试发现,tmp数组中有序数字,并没有被我们完整的拷贝回去
原本是2 5拷贝回去变成了2 2,这个问题的根源很明显是memcpy函数调用有问题
一看,哭笑不得,写了俩sizeof,魔怔了属于是
修改之后,没问题啦!
4.2递归源码
这里给出最终的源码,一些地方写了注释
//_代表这是子函数
void _MergeSort(int* a,int* tmp, int begin, int end)
{
if (begin >= end){
return;
}
int mid = (begin + end) / 2;
_MergeSort(a, tmp, begin, mid);
_MergeSort(a, tmp, mid+1 , end);
//printf("归并[%d,%d][%d,%d]\n", begin, mid, mid+1, end);
int begin1 = begin, end1 = mid ;
int begin2 = mid+1 , end2 = end;
int cur = begin;
while (begin1 <= end1 && begin2 <= end2)
{
//取小的放到新数组中
if (a[begin1] < a[begin2]) {
tmp[cur++] = a[begin1++];
}
else {
tmp[cur++] = a[begin2++];
}
}
//第一个循环结束,并不代表归并完毕,可能只有一个数组的数据跑完了
//我们需要将另外一个数组的数据全部拷贝到tmp中(因为剩下的的数据已经有序)
while (begin1 <= end1) {
tmp[cur++] = a[begin1++];
}
while (begin2 <= end2) {
tmp[cur++] = a[begin2++];
}
memcpy(a+begin,tmp + begin, ((end - begin +1)*sizeof(int)));
}
//归并排序
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(n * sizeof(int));
if(tmp==NULL){
printf("malloc failed\n");
exit(0);
}
_MergeSort(a, tmp, 0, n-1);
free(tmp);
tmp = NULL;
return;
}
4.3非递归实现
归并排序的非递归无法用栈来实现,因为我们不能把之前的大区间全给出栈了,因为这些区域还需要在最后重新进行归并!
- 利用循环来控制不同的区间,由小到大,直到
gap=n跳出循环 - gap是归并数据的个数,gap=1代表1个数归并,gap=2代表两两归并
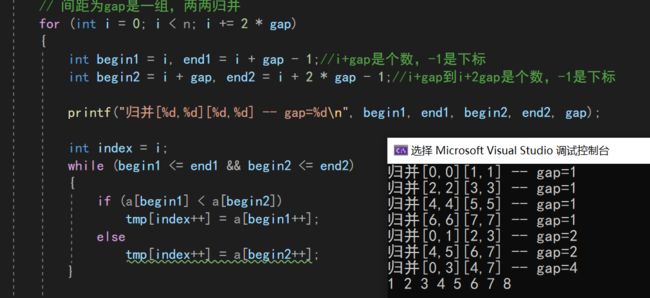
根据上面的思路,我们可以写出下面的范围循环
int gap = 1;
while (gap < n)
{
// 间距为gap是一组,两两归并
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
//i+gap是个数,再-1是下标
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//i+gap到i+2gap是个数,再-1是下标
//打印调试大法
printf("归并[%d,%d][%d,%d] -- gap=%d\n", begin1, end1, begin2, end2, gap);
}
gap *= 2;
}
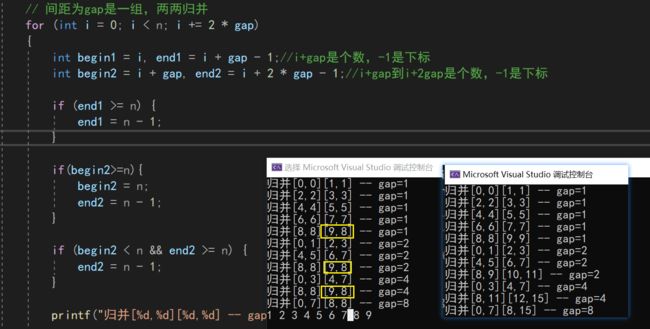
跑一遍之前的测试用例,发现能搞定!这不就完事了吗?
并没有!这里gap的操作都是*2,而且我们给的数组是偶数个,正好对的上
如果我们再加一个数呢?程序打印出了每一层的递归区间,但是没有打印出最终的结果——因为这里在最后free的时候发现了数组越界访问
小知识,数组越界一般都是在free的时候检查到的
接下来要做的事就是控制下标区间,避免它越界
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
| begin | end |
|---|---|
| i | i+gap-1 |
| i+gap | i+2*gap-1 |
仔细分析过后,发现当gap=2,i=8的时候,就会出现+gap之后越界的情况
而会出现越界情况的,不止有end2,end1和begin2都可能会出现
我们需要做的就是把越界的下标修正为不越界的下标
- end1越界,修正为不越界即可
- begin2和end2都越界,修正为非法区间
begin2>end2 - begin2不越界,end2越界,修正end2即可
修正下标后,可以看到程序已经正常排序出了序列
虽然打印出来的范围还是有越界的下标,但是这个是begin>end的非法区间,不符合程序运行的条件,就不会产生越界
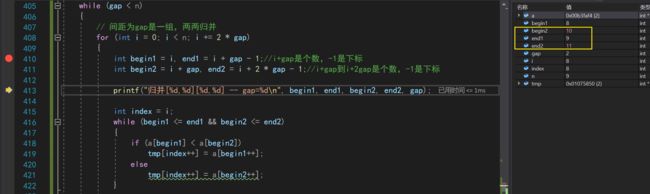
4.3.1 条件断点
这里还有一个骚操作,比如我们已经知道了是8-9的下标越界,这样我们就可以设置一个断点,来直接F5跳到那个情况,而不需要疯狂按F10
// 条件断点,用于调试
if (begin1 == 8 && end1 == 9 && begin2 == 10 && end2 == 11)
{
int x = 0;
}
这样我们的非递归实现也搞定啦!
//非递归
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
int gap = 1;
while (gap < n)
{
// 间距为gap是一组,两两归并
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;//i+gap是个数,-1是下标
int begin2 = i + gap, end2 = i + 2 * gap - 1;//i+gap到i+2gap是个数,-1是下标
if (end1 >= n) {
end1 = n - 1;
}
if(begin2>=n){
begin2 = n;
end2 = n - 1;
}
if (begin2 < n && end2 >= n) {
end2 = n - 1;
}
//printf("归并[%d,%d][%d,%d] -- gap=%d\n", begin1, end1, begin2, end2, gap);
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
tmp[index++] = a[begin1++];
else
tmp[index++] = a[begin2++];
}
while (begin1 <= end1)
tmp[index++] = a[begin1++];
while (begin2 <= end2)
tmp[index++] = a[begin2++];
}
memcpy(a, tmp, n * sizeof(int));
gap *= 2;
}
free(tmp);
}
4.4归并排序的时间/空间复杂度
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N),创建数组的消耗
5.计数排序
计数排序的基本思路:利用数组的下标作为映射,遍历到x,在数组的x下标处++一次。最后再依照下标顺序将之前遍历到的数倒出来,就形成了正序序列。
我在网上找来了一个很棒的动图(这个好像在很多博客里面都有)
这个排序的思路就不难了,但有一点我们可以优化一下
假设我们的序列是从300开始,而不是从0开始,那么开辟一个301个数的数组显然会浪费300之前的下标(因为并没有值)
这时候我们可以找出数组的范围,开辟一个对应范围长度的数组,再利用相对映射的方式,来进行计数
最后的代码如下
void CountSort(int* a, int n)
{
int min = a[0], max = a[0];
for (int i = 1; i < n; ++i)
{
if (a[i] < min)
min = a[i];
if (a[i] > max)
max = a[i];
}
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
assert(count);
memset(count, 0, sizeof(int) * range);
// 计数
for (int i = 0; i < n; ++i)
{
count[a[i] - min]++;
}
// 排序
int j = 0;
for (int i = 0; i < range; ++i)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
}
5.1计数排序的特性
- 时间复杂度:O(range+N)
- 空间复杂度:O(range)
计数排序适用于范围集中的数,不然会产生很大的空间浪费
计数排序可以排序带负数的序列,同样是通过映射的方式
但是计数排序只能排序整型数据,浮点类型是搞不定的
看到这里,我们的八大排序就已经讲解完毕啦!
不知道我讲解的够不够清楚呢?
下面还有一个小点,就是关于排序算法的稳定性
6.排序算法的稳定性
估计很多人和我一样,都对这个“稳定性”有错误的理解
我本来以为,稳定性代表的是排序算法的时间波动大不大
实际上的稳定性,是算法对于某一个数的处理好不好
比如下图,假设大家在考试,从上到下依次是交卷的顺序,我们发现王舞和李四的成绩相同,但是李四先交的卷。对于评判来说,当然是先交卷且分高的同学牛逼一点
所以依照分数排序的时候,我们应该把李四排在王舞之前
但有些算法在排序的时候,就做不到这一点
这里对直接选择排序做一个简单的解释
因为两个3的位置调换,就导致排序不够稳定
实际上,所有需要进行选择交换的排序都不够稳定
但是冒泡排序在交换的时候是严格保证大的数在后头,相等的数不交换的思路,所以冒泡排序是稳定的
6.1稳定性表格
| 排序算法 | 稳定性 |
|---|---|
| 直接插入 | 稳定 |
| 希尔 | 不稳定 |
| 直接选择 | 不稳定 |
| 堆排序 | 不稳定 |
| 冒泡 | 稳定 |
| 快速排序 | 不稳定 |
| 归并排序 | 稳定 |
| 计数排序 | 不稳定 |
7.利用clock函数查看排序耗时
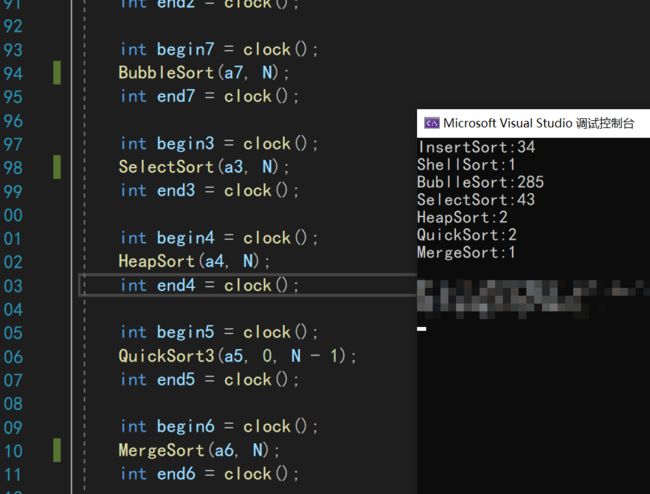
排序算法写完后,我们可以通过调用clock函数来查看每一个排序的耗时
先利用srand和time函数来创建随机数数组,在调用每一个函数,来查看它们排序的耗时
注意:请确认排序算法代码无误,再进行本操作
由于代码过长,这里只给出某一个排序的计时代码,其他就CV一下就OK了
srand(time(0));
const int N = 10000;
int* a1 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();//生成随机数 数组
}
int begin1 = clock();//读取系统时钟
InsertSort(a1, N);
int end1 = clock();//再读取系统时钟
//二者相减得出该函数运行时长
printf("InsertSort:%d\n", end1 - begin1);
free(a1);
运行结果:
结语
到这里,排序的绝大数知识点就讲解完毕啦!
本篇博客画了很多图,还挺不容易的,还请大家点赞支持一下!
特别是那两个看起来很简单的动图,实际上麻烦的很
球球了,点个赞呐!