【递归与回溯算法】汉诺塔与八皇后问题详解

本篇主要解决内容：

• 汉诺塔问题 ⭐️
• 八皇后问题 ⭐️

❤️ 个人主页：Nezuko627 欢迎来访~~~

---

1 汉诺塔问题

1.1 汉诺塔问题概述

✈️ 相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

1.2 思路分析

我们先在脑海里模拟一遍：假如 A杆处有从小到大的 2 个盘，我们需要怎么做呢？

1. 将小盘由 A 杆移动到 B 杆； 即 A -> B;
2. 将大盘由 A 杆移动到 C 杆；即 A -> C;
3. 将小盘由 B 杆移动到 C 杆；即 B -> C;
4. 模拟完成。

对于汉诺塔问题我们可以采用递归的思想解决问题，对递归有疑问的小伙伴可以看一下这篇文章：【JavaSE】深入浅出悟透递归

我们将问题分为两种情况：
⭐️ star 1：A 杆只有 1 个盘

对于这种情况，我们只需要将 A 杆上的盘直接移动到 C 杆即可完成任务。

⭐️ star 2：A 杆有多个盘

对于多个盘我们可以看成两个部分，即上面的所有盘与最下面的盘

1. 将上面的所有盘借助 C 杆 移动到 B；
2. 将最下面的盘直接移动到 C 杆；
3. B 杆上面的盘继续借助 A 杆移动到 C 杆。

1.3 代码实现（Java）

/**
 * 汉诺塔问题
 */
public class HanoiTower {
    public static void main(String[] args) {
        hanoi(2, 'A', 'B', 'C');  // 测试两个盘子的情况
    }
    
    // num 表示盘子的个数, abc分别表示 a b c位置
    private static void hanoi(int num, char a, char b, char c){
        // 如果只剩一个盘子, 只需要移动到 c 处
        if(num == 1){
            System.out.println(a + "->" + c);
        }else {
            // 如果有多个盘子，我们可以看成两个部分：最上面的 num - 1个 与 最下面的1个（最下面的只需要由a放到c）
            // 先移动上面所有的盘从 a 借助 c 移动到 b
            hanoi(num-1, a, c, b);
            // 把最下面的盘子从 a 直接移动到 c
            System.out.println(a + "->" + c);
            // 把 b 的所有盘子从 b 借助 a 移动到 c
            hanoi(num-1, b, a, c);
        }
    }
}

1.4 结果验证

1.当 A 杆只有 1 个盘的时候，结果如下：

2. 当 A 杆有 2 个盘的时候，结果如下：

3. 当 A 杆有 3 个盘的时候，结果如下：

---

2 八皇后问题

2.1 八皇后问题概述

✈️ 八皇后问题（英文：Eight queens），是由国际象棋棋手马克斯·贝瑟尔于1848年提出的问题，是回溯算法的典型案例。问题表述为：在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。如果经过±90度、±180度旋转，和对角线对称变换的摆法看成一类，共有42类。计算机发明后，有多种计算机语言可以编程解决此问题。

2.2 思路分析

大体思路是先将棋盘初始化，进行8次循环， 每次循环放置一个皇后并检查是否满足条件，如果满足则放置皇后并登记皇后位置，如果不满足，则回退，继续搜索下一步是否可以放置皇后。 直到八个皇后放置完毕，记录一次结果。

2.2.1 问题划分与分析

该问题同样可以用递归来解决，可以将问题划分成：

1. 找到 N-1 个皇后的位置
2. 找到第 N 个皇后的位置

但如果只使用递归的话，只能求出一种合适的解，为了解出所有可能结果，我们需要使用到回溯算法。

2.2.2 涉及到的数据结构分析

	// 第n个皇后所占位置的列号 place[1] = 2则表示第2个皇后在第2行3列
   int[] place
    // 标志数组, true为不可放置,notPlaced[1] = true表示第2列不可放置
   boolean[] notPlaceable
    // 存储结果数量
	int[] sum = {0};
    // d1数组存储上对角线,d2数组存储下对角线
    // false认为对角线上有皇后，不可以占领
    boolean[] d1 
    boolean[] d2 

2.2.3 上下对角线与行列的关系

对于斜线上是否还能存在皇后，我们分为上对角线和下对角线两个方向，通过 d1 d2两个数组分别标记，对角线与行号列号的关系分析如下：
star 1：上对角线
我们如果将每一位置的 行号 与 列号 相减，则会得到下面这张上对角线图：

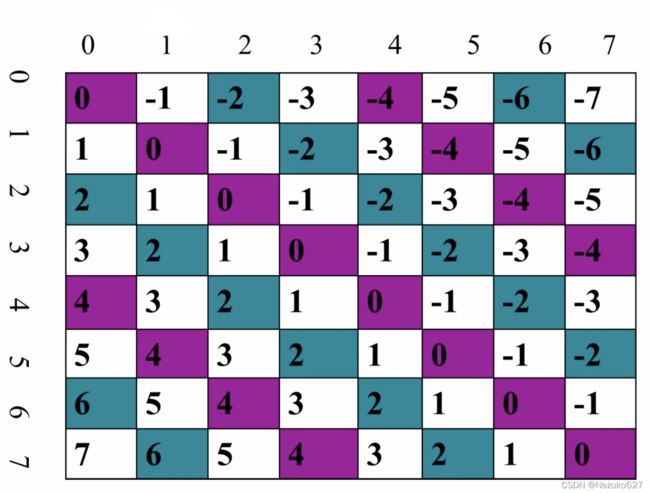
解释： 如果我们放置了一个皇后在 （2，3）这个位置，需要判断他的一个斜线方向是否有皇后，则只需要判断标记数组 2-3=-1 (-1是一条上对角线)这一索引是否被标记即可。
但是，数组的索引是从0开始的，我们观察一下图，最小值是 -7，因此我们只需要计算 行号 - 列号 + 7即可，此时图中为 -7 的位置均为 0 ，-6的位置索引为1，以此类推。
这里小伙伴可能会有疑问，如果只是为了满足数组的索引从0开始，那我们也可以求行号与列号的差的绝对值呀！ 这是个好想法，但是如果取绝对值，则无法用数组的索引唯一标记一个斜线 ，比如：-1变成1，则1就表示两条斜线。

star 2：下对角线
下对角线的计算方式与上对角线类似，我们需要计算 行号与列号的和，得到的下对角线图如下：

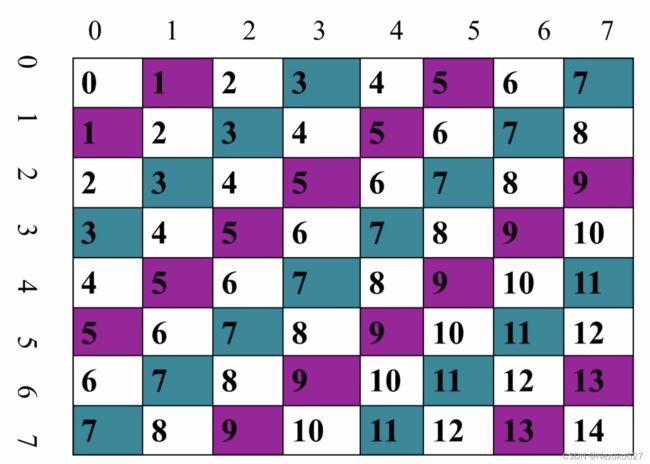
2.3 代码实现（Java）

注意：这里sum使用数组声明，原因在于 Java的值传递与引用传递，看看这篇文章你就直到为什么这样做啦！---->【JavaSE】数组的赋值机制（值拷贝与引用传递）、数组拷贝、数组反转与数组扩容

public class EightQueen {
    // 第n个皇后所占位置的列号 place[1] = 2则表示第2个皇后在第2行3列
    static int[] place = new int[8];
    // 标志数组, true为不可放置,notPlaced[1] = true表示第2列不可放置
    static boolean[] notPlaceable = new boolean[8];
    // 存储结果数量
    static int[] sum = {0};
    // d1数组存储上对角线,d2数组存储下对角线，false认为对角线上有皇后，不可以占领
    static boolean[] d1 = {true, true, true, true, true, true, true, true, true, true, true, true, true, true, true};
    static boolean[] d2 = {true, true, true, true, true, true, true, true, true, true, true, true, true, true, true};

    // 8皇后具体算法
    private static void generate(int n){
        // 每个皇后都有8种可能的列
        for (int col = 0; col < 8; col++) {
            // 判断是否可以放置
            if(!notPlaceable[col] && d1[n-col+7] && d2[n+col]){
                place[n] = col;  // 在 n 行 col 列摆放皇后
                notPlaceable[col] = true;  // 占领该列
                d1[n-col+7] = false;  // 占领上对角线
                d2[n+col] = false;  // 占领下对角线
                if(n < 7)
                    generate(n+1);
                else{
                    sum[0]++;  // 解的个数加1
                    myPrint();  // 打印一种结果
                }
                // 回溯用于求其他结果
                notPlaceable[col] = false;
                d1[n-col+7] = true;
                d2[n+col] = true;
            }
        }
    }

    // 打印每种结果
    private static void myPrint(){
        for (int i = 0; i < place.length; i++) {
            System.out.print(place[i]+1 + " "); // 打印结果直接是第几列
        }
        System.out.println();
    }

    // 主函数
    public static void main(String[] args) {
        generate(0); // 求解8皇后
        System.out.println("共有的解法: " + sum[0]);
    }
}

2.4 结果验证

结果共有 92 个解，结果太长 这里只截取部分展示！

---

写在最后

以上便是本文的全部内容啦，后续内容将会持续免费更新，如果文章对你有所帮助，麻烦动动小手点个赞 + 关注，非常感谢 ❤️ ❤️ ❤️ !
如果有问题，欢迎私信或者评论区！
共勉：“你间歇性的努力和蒙混过日子，都是对之前努力的清零。”