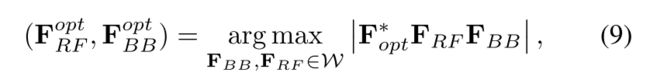【混合预编码文献总结】探索大佬的混合预编码研究历程之路2:如何将混合预编码设计问题一步步转化为约束最小二乘问题
【混合预编码文献总结】探索大佬的混合预编码研究历程之路2:如何将混合预编码设计问题一步步转化为约束最小二乘问题
- 写在前面
- 前言
- 背景
- 一、本文贡献
- 二、系统模型
-
- “单用户多天线多流”系统模型
- 用户端经过处理后的信号模型
- 基于簇的稀疏散射信道
- 三、单用户毫米波系统的混合预编码问题转化
-
- 第一步:原问题模型——最大化可实现速率
- 第二步:混合预编码和混合接收编码问题解耦
- 第三步:最大化 F R F F B B \mathbf{F}_{\rm RF}\mathbf{F}_{\rm BB} FRFFBB在最优全数字预编码上的投影
- 第四步:最小化 最优全数字预编码矩阵和混合预编码矩阵的残差的F范数
- 第五步:选择最好的Nrf个基向量然后找到它们最优的基带组合
- 四、基于基追踪(OMP)的混合预编码设计算法
- 五、precoder和combiner存在先后设计顺序问题
- 六、仿真结果
- 七、对本文的思考
- 参考文献
写在前面
本专栏的目的:总结混合预编码研究领域中的一个大佬团队(Robert W. Heath Jr,Ayach Omar El,Alkhateeb Ahmed等人)从2012年至今所发表的一些具有代表性的文章,目的在于探索大佬们一步步走上这个领域的顶端的科研历程,也作为自己学习研究过程的记录,同时与各位同学一起学习、探讨。
前言
在上一篇文章(【混合预编码文献总结】探索大佬的混合预编码研究历程之路1:信道奇异向量和阵列响应向量的关系)讲到,Omar EI 在假设天线数目趋于无穷大的情况下,信道的奇异向量收敛于阵列响应向量。那么我们知道实际情况下,目前5G基站的天线数目普遍在64、128和256这样的数量级上,它们远远要小于理论推导所假设的无穷大情况,那么在这种情况下,如何求解混合预编码问题呢?
背景
1、传统通信系统中,每个天线配有专用的射频链,这使得系统能够根据不同的准则对信号的幅度和相位进行灵活调整,但在Massive MIMO 通信系统中,由于大规模天线部署,若配备相同数量的射频链则会产生大量的能耗,因此需要减少射频链的数目。
为了解决这一问题,本文之前的研究工作提出过antenna seletion和equal gain transmission,但这些方法都不是针对大规模天线场景,具体来说,他们都是在具有丰富散射的瑞利信道下进行的算法设计,而Massive MIMO 毫米波信道的重要特征之一就是稀疏散射,即dominant path的数量是有限的。
2、由于毫米波段波长较短,这使得在有限尺寸的阵列中部署超大规模的天线阵元成为可能,超大规模阵列也更有利于形成高指向性、高增益的波束,从而更有效地克服路径损耗、导频污染等问题。
3、在毫米波通信系统中,BS为了节省功耗,将用于传统通信系统的全数字预编码方案替换为由基带预编码和模拟预编码组成的混合预编码方案,射频链的数目相比于天线数目很小,因此可以降低产生于射频链的功耗。但与此同时,出现两个问题:i)对于信号的幅度和相位调节不再像全数字预编码一样完全灵活,因为不是每个天线都连接一条专属的射频链,这造成对于每个天线阵元的信号的幅度调节不灵活;ii)因为模拟预编码器是由移相器网络组成,而移相器只能实现相位的调节,意味着模拟预编码器的设计要遵循“恒模约束”,这使得混合预编码设计问题变得极其复杂,是一个NP-hard问题。
3、在传统MIMO预编码的设计和性能分析时,通常假设在具有丰富衰落的瑞利衰落信道下(scattering levels are too rich),但毫米波信道的高路损使信道稀疏散射特性。
因此本文采用稀疏散射信道模型(基于extended S-V 的有限散射信道)
一、本文贡献
1、本文设计预编码算法主要着眼于三点:
- 考虑模拟预编码的移相器网络的恒模约束
- 考虑超大规模天线阵列
- 考虑稀疏散射信道
2、本文提出了一种基于 matrix approximation 的算法,试图用基带预编码和模拟预编码来逼近最优无约束数字预编码矩阵。
3、通过本文,可以看到作者是如何将precoding 问题从最初的 SE maximization 问题一步步转化为一个sparsity constrained least square 问题,然后使用基追踪的方法解决。
4、对于BS和UE两侧射频链数目不同时,precoding和combining不是同时进行设计的,而应该先设计射频连数目少的一方。
二、系统模型
“单用户多天线多流”系统模型
基站端 N t N_t Nt根天线配备 N R F t N_{RF}^t NRFt个射频链发送 N s N_s Ns个数据流,用户端 N r N_r Nr根天线配备 N R F r N_{RF}^r NRFr个射频链接收 N s N_s Ns个数据流。
用户端经过处理后的信号模型
基于簇的稀疏散射信道

其中, L L L为cluster数量,每个cluster中只有一个ray, α l \alpha_l αl表示第 l l l个路径的复增益,服从 ( 0 , 1 ) (0,1) (0,1)正态分布, Λ t ( ϕ l t , θ l t ) \Lambda^t(\phi_l^t,\theta_l^t) Λt(ϕlt,θlt)和 Λ r ( ϕ l r , θ l r ) \Lambda^r(\phi_l^r,\theta_l^r) Λr(ϕlr,θlr)表示指向性天线在对应AoD和AoA的增益(式4所示), α t \boldsymbol\alpha_t αt和 α r \boldsymbol\alpha_r αr表示发送天线阵列响应向量和接收天线阵列响应向量, ϕ l r \phi_l^r ϕlr和 ϕ l t \phi_l^t ϕlt表示水平方向(方位角)的到达角和发射角, θ l r \theta_l^r θlr和 θ l t \theta_l^t θlt表示垂直方向(俯仰角)的到达角和发射角。

本文假设BS和UE都部署均匀面阵UPA,天线阵列响应向量可表示为
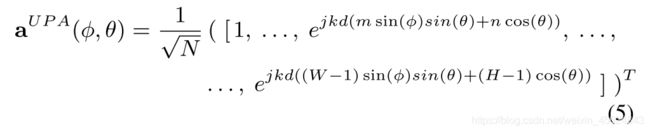
其中W为y轴方向的阵元数目,H为z轴方向的阵元数目,因此总的天线阵元数目 N = W H N=WH N=WH。
三、单用户毫米波系统的混合预编码问题转化
第一步:原问题模型——最大化可实现速率
混合预编码矩阵和接收矩阵的问题可表示为设计矩阵 F R F , F B B , W R F , W B B \mathbf{F}_{\rm RF},\mathbf{F}_{\rm BB},\mathbf{W}_{\rm RF},\mathbf{W}_{\rm BB} FRF,FBB,WRF,WBB以使得速率最大化,其中模拟预编码矩阵和模拟接收矩阵中的项要符合恒模约束,同时基带预编码应满足功率约束,则原问题如下所示
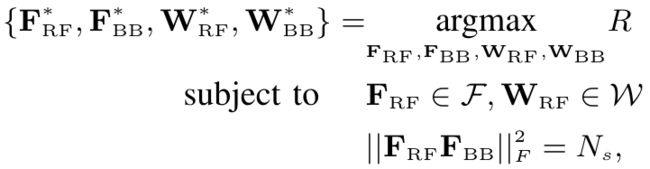
其中Achieved rate

第二步:混合预编码和混合接收编码问题解耦
- 将原问题解耦为两个问题,这样UE在得到信道估计结果之后只需要设计自己的hybrid combiner,由BS设计自己的hybrid precoder,因此设计混合预编码的问题模型可以近似为如下所示,即将接收端的combiner分离,等价于接收端使用了最大比合并算法MRC对接收信号进行处理。
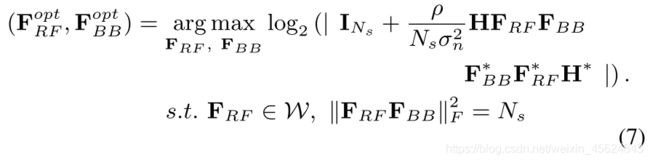
第三步:最大化 F R F F B B \mathbf{F}_{\rm RF}\mathbf{F}_{\rm BB} FRFFBB在最优全数字预编码上的投影
- 该问题仍然是一个难解的问题,需要进一步近似才能使用一些解凸优化问题的方法。
第四步:最小化 最优全数字预编码矩阵和混合预编码矩阵的残差的F范数
为了得到一个实际的可行解,需要将目标函数 ∣ F o p t ∗ F R F F B B ∣ |\mathbf{F}^*_{\rm opt}\mathbf{F}_{\rm RF}\mathbf{F}_{\rm BB}| ∣Fopt∗FRFFBB∣替换为 trace ( F o p t ∗ F R F F B B ) \text{trace}(\mathbf{F}^*_{\rm opt}\mathbf{F}_{\rm RF}\mathbf{F}_{\rm BB}) trace(Fopt∗FRFFBB),它实际上根据算术几何平均不等式得到的原目标函数的一个上届。

由最大化迹等价为最小化 最优全数字预编码矩阵和混合预编码矩阵的残差的F范数,则问题模型转化为

可以看到这实际上是一类普鲁克问题的形式,只是多了一个恒模约束。
- 正交普鲁克问题:目标是寻找一个旋转矩阵,将一个点集旋转到离另一个点集最近的位置(需要提前知道两个点集中每个点的对应关系),其数学模型可表示为
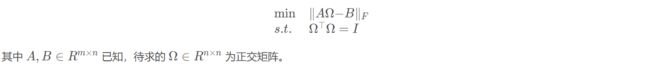
最优的全数字预编码是矩阵奇异值分解得到的右酉阵中的主导向量,由信道矩阵式(3)可以看出阵列响应向量同样组成了一个集合,并且“likely”构成了一组和奇异向量构成的空间相同的基向量,也就是说,最优预编码的列可以用阵列响应向量的线性组合来表达。启发于此,我们用 F B B \mathbf{F}_{\rm BB} FBB作为权重,对阵列响应向量进行线性组合,来逼近最优的全数字预编码,问题模型可以转化为如下所示。
- 我们举一个特殊情况的例子来说明,如果基站射频链数大于等于路径数,那么相当于所有的基都可以被选择,然后对他们进行线性加权, F o p t \mathbf{F}_{\rm opt} Fopt就可以完全被恢复,也就是式(11)的残差等于0。
但这种假设是不合理的,因为通常基站射频链数目小于路径数。
第五步:选择最好的Nrf个基向量然后找到它们最优的基带组合
因此可以构成一个基向量组合 A t = [ a t ( ϕ 1 t , θ 1 t ) , . . . , a t ( ϕ L t , θ L t ) ] ∈ C N t × L \mathbf{A}_{t}=[\mathbf a_t(\phi_1^t,\theta_1^t),...,a_t(\phi_L^t,\theta_L^t)]\in \mathbb{C}^{N_t \times L} At=[at(ϕ1t,θ1t),...,at(ϕLt,θLt)]∈CNt×L,和一个权重矩阵 F ~ B B ∈ C L × N s \widetilde \mathbf{F}_{BB}\in \mathbb{C}^{L \times N_s} F BB∈CL×Ns。为了满足射频链数目的约束,对 F ~ B B ∈ C L × N s \widetilde \mathbf{F}_{BB}\in \mathbb{C}^{L \times N_s} F BB∈CL×Ns的非零行数进行约束。

到目前为止,我们已经把原问题转化为了只有一个变量的稀疏约束最小二乘问题,因此一些成熟的方法可以套用进来。
四、基于基追踪(OMP)的混合预编码设计算法
- 步骤1:找最大投影:从 A t \mathbf{A}_{t} At中找到与最优全数字预编码矩阵投影最大的列向量
- 步骤2:更新支撑集:将步骤1找到的列向量放在支撑集中作为 F R F \mathbf{F}_{RF} FRF的一列
- 步骤3:更新当前解:此时已知 F R F \mathbf{F}_{RF} FRF,相当于一个最小二乘问题(如式(11)),与因此解最小二乘问题可以得到当前的闭式解即为 F B B \mathbf{F}_{BB} FBB
- 步骤4:更新残差:原最优全数字预编码矩阵减去基于当前支撑集 F R F \mathbf{F}_{RF} FRF和对应权重 F B B \mathbf{F}_{BB} FBB的贡献。
- 重复上述步骤1到4,迭代 N R F t \mathbf{N}^t_{RF} NRFt轮,即选出 N R F t \mathbf{N}^t_{RF} NRFt个波束赋形向量。
- 最后,进行归一化以符合功率约束。

五、precoder和combiner存在先后设计顺序问题
- 简单来讲,BS和UE的射频链通常不相同,那么使用多少个射频链要 min { N R F t , N R F r } \text{min}\{\mathbf{N}^t_{RF},\mathbf{N}^r_{RF}\} min{NRFt,NRFr} 来决定。
- 举个例子,假如接收端只有一条射频链,因此支撑集中只有一个阵列响应向量,在这种情况下,只单纯为了达到接近 F o p t \mathbf{F}_{opt} Fopt而设计 F R F \mathbf{F}_{RF} FRF会造成同时存在几个方向的入射信号但接收端只能从一个方向接收的情况,会造成接收能量的损耗。
- 因此,使用如下准则,来进行有顺序的precoder和combiner求解。
六、仿真结果
未完待续。。。
七、对本文的思考
1、相比于【混合预编码文献总结】探索大佬的混合预编码研究历程之路1:信道奇异向量和阵列响应向量的关系 中Omar EI 在假设天线数目趋于无穷大的情况下理论推导出一些重要且有趣的结论,是在marzetta的Massive MIMO优势结论的基础上,关于混合预编码的思考;本文考虑64Tx 16Rx和 256Tx 64Rx两种具有实际意义的场景,对问题进行建模然后一步步转化为一个稀疏恢复的问题,利用基追踪的方法进行求解,并得到了不错的仿真结果,这是对混合架构下进行预编码的可能性(大大降低功耗并保证一定的性能)的一个有效验证。
2、Omar在本文中将难解的原问题模型通过一步步的转化,最终得到一个“有法可用”稀疏恢复问题,其中最重要的思想是对矩阵逼近过程中的矩阵相似性从不同数学角度的衡量,让在直觉上看起来”理所应当“的逼近想法,用数学语言严格表述出来,这对于我们是有启发性的:对任何问题的数学建模和方法论都应该有严谨的逻辑,然后用简洁且准确的数学语言表示出来。
参考文献
Low complexity precoding for large millimeter wave MIMO systems.