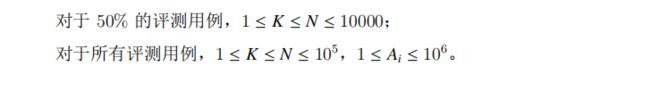算法零基础到省一的“混”奖经历【第十三届蓝桥杯 Python B组】
文章目录
- 前言
- 起点
-
- 浅谈蓝桥杯含金量及赛制
- 我对蓝桥杯的看法及参赛建议
- 我的备赛出发点
- 备赛过程(必知必会的基础算法目录)
- 省赛复盘(侧重讲赛场上的体验)
-
- 试题 A
-
- 题目描述
- 问题分析
- 代码实现
- 试题 B
-
- 题目描述
- 问题分析
- 代码实现
- 试题 C
-
- 题目描述
- 问题分析
- 代码实现
- 试题 D
-
- 题目描述
- 问题分析
- 代码实现
- 试题 E
-
- 题目描述
- 问题分析
- 代码实现
- 试题 F
-
- 题目描述
- 问题分析
- 代码实现
- 试题 G
-
- 题目描述
- 问题分析
- 代码实现
- 试题 H
-
- 题目描述
- 问题分析
- 代码实现
- 试题 I
-
- 题目描述
- 问题分析
- 代码实现
- 试题 J
-
- 题目描述
- 问题分析
- 代码实现
- 总结
前言
| 2022年第十三届蓝桥杯省赛算是结束了,趁五一期间不是很忙写一下自己的参赛心得,是对过去的参赛经历做的总结,也是对未来国赛的展望。希望对博主自身有帮助,也希望对大家有所帮助。下图是博主省赛中取得的成绩,一等奖一共有70多位我是第30多位,排名不算很高但我愿意跟你分享我的经历,帮助你也获奖。如何手到擒来且听我细细道来。 |
![]()
起点
浅谈蓝桥杯含金量及赛制
这一章节将会以如下几点进行介绍
- 含金量
- 参赛人数及获奖比例
- 赛制&比赛时间
- 赛事划分的类别
- 参赛形式
| 含金量: |
| 蓝桥杯全国软件和信息技术专业人才大赛是由中华人民共和国工业和信息化部人才交流中心主办,国信蓝桥教育科技(北京)股份有限公司承办的计算机类学科竞赛 。截至2022年2月,蓝桥杯全国软件和信息技术专业人才大赛已举办12届 ,正在进行第13届。蓝桥杯入选了全国普通高校学科竞赛榜可以进行综合测评加分、单项奖学金评定。有助于升学考研。 |
| 参赛人数: |
| 截止目前已累计参赛人数50w+合作的高校企业有1600+。而且参赛的人数仍在每年递增。 获奖的比例非常的可观,按比例获奖几乎一半的人都有奖。当然有一个最低分数线,如果比例到了指定的位置没有过指定分数线的话将会对你的奖项进行降级。 |
| 赛制&比赛时间: |
| 蓝桥杯其他的赛道我不知道,程序设计赛道的话是十道程序设计题,往年是五道填空五道编程,今年由于疫情线上线下结合比赛改为了两道填空八道编程。比赛期间提交代码后不会得到及时反馈OI赛制。只有比赛结束后过1-2周才会出结果。出题会根据比赛大纲进行出题,目前来说出题质量连年上升。 报名&比赛时间: 这个不是很确定,但是一般都是下半年开始报名,第二年上半年进行比赛,分为省赛与决赛。每场比赛缴费300元(拿奖之后学校会报销),拿到不错的名次还会有奖励,不同的学校有不同的政策。 想报名的小伙伴可以在每年的下半年多留意蓝桥杯官网https://dasai.lanqiao.cn/ 比赛时间一般为上午,不同赛道比赛时长不一样,每一届官网都会很早很早都给出比赛时间。 |
| 赛事划分的类别: |
| JAVA软件开发具有正式全日制学籍并且符合相关科目报名要求的研究生、本科及高职高专学生(以报名时状态为准)。设研究生组、大学A组、大学B组、大学C组 |
| C/C++程序设计具有正式全日制学籍并且符合相关科目报名要求的研究生、本科生及高职高专学生(以报名时状态为准)设研究生组、大学A组、大学B组、大学C组 |
| Python程序设计具有正式全日制学籍并且符合相关科目报名要求的研究生、本科、高职高专及中职中专学生(以报名时状态为准)设研究生组、大学A组、大学B组、大学C组。 |
| Web应用开发具有正式学籍的在校全日制研究生、本科、高职高专及中职中专学生(以报名时状态为准)设大学组和职业院校组。 |
| 嵌入式设计与开发具有正式学籍的在校全日制研究生、本科及高职高专学生(以报名时状态为准)设大学组 |
| 单片机设计与开发具有正式学籍的在校全日制研究生、本科、高职高专及中职中专学生(以报名时状态为准)设大学组和职业院校组。 |
| 物联网设计与开发具有正式学籍的在校全日制研究生、本科及高职高专学生(以报名时状态为准)设大学组 |
| EDA设计与开发具有正式学籍的在校全日制研究生、本科及高职高专学生(以报名时状态为准)设大学组 |
| 参赛形式: |
| 没有疫情及重大突发事件的话,会进行线下比赛。如果线上参赛的话需要摄像头双机位监考,个人感觉还是很合规的。只要好好努力一定会取得不错的成绩。 |
我对蓝桥杯的看法及参赛建议
| 我对蓝桥杯的看法 |
| 蓝桥杯出题的话会有两道左右的签到题,只考编程技巧一般来说会点编程就会做。其余的题目按测试点给分(也就是说暴力进行求解的话也会得到一部分分数)我认为这一点很亲民,暴力写的话只会得到一部分分数大概有40%以下,如果没有使用暴力方法解题的题目估计我写不出几道。也就拿不到省一了,可以暴力解题但是不要妄想使用暴力解法求解全部测试点,想要AK一道题目就必须精心优化算法,这也是拉开参赛选手区分度的一个重要点之一。大家应该秉着收获的心态去参加比赛,毕竟比赛是双向的,在比赛中得到快速地成长才是重点。我介意大家在时间充足的话可以参加蓝桥杯比赛一试,相信收获会让你灰常的惊喜。 |
| 我建议参赛的组别 |
| 参赛的话首先选择一个你喜欢的语言,如果没有的话我推荐参加Python,因为参加Python组你会避开很多Acmer。容易得奖再加上Python近些年来非常的热火,数据分析、人工智能..... |
我的备赛出发点
| 我是一名没有任何基础的选手,并且第一次参加蓝桥杯,如果非要找出来一点基础的话,就是我完整的学习过数据结构与算法,对树与图的几个算法有一定的了解,报名时间是去年12月左右,自从报了名我就整日进行划水,几乎没有学习过算法题直到2022年2月多返校之后,某天我注意到蓝桥杯省赛将至。我还什么也不会便下定决心开始了我的刷题之旅,我先是借了同学一本算法入门白皮书(刘汝佳写的)见下图1。虽然书很旧了,但是里面的题目依旧灰常的经典(介意大家整一本看一看)。看完之后再找些题目刷一刷,博主刷的时候是散刷,一般会在csdn上先检索一下有没有博主推荐的,有的话找到原题刷一刷。或者会看bilibili上博主分享的题目,在学习算法题的时候优先掌握算法思想(因为题目的变化会千奇百怪),我们抓住其本质即可。 |
备赛过程(必知必会的基础算法目录)
着重看了以下几个算法与数据结构
学习的话可以在cddn上进行搜索,咱们c站大佬讲的都很棒。理解了思想或者说理解了这是干什么的之后就找几个题
刷一刷,不要直接看题解,也不要一直死磕。感觉自己确实不会就看题解。有一点思路就不要看。如果一直被题吊着
的话也不行最多想半小时如果还没思路的话就看题解。如果是没有任何基础的选手,建议直接看题解。先把一片题过一遍之后再去刷题。没有知识点支撑刷题万分痛苦。
| 算法 | |
| 搜索(主要掌握一下数据结构中的二分法、DFS、BFS) 十大排序 进制转换 字符串处理(回文数系列、分割、合并、时间日期字符串转换等) 高精度数值计算 GCD、LCM(也就是求最大公因数、最小公倍数) 素数筛(朴素素数筛、埃氏筛、线性筛) 前缀和(一维、二维) 前缀最值、后缀最值 差分(一维、二维) 倍增 尺取法 快速幂(数值快速幂、矩阵快速幂、矩阵加速数列计算) 算术基本定理 同余取模 完全平方数 递归(分治)思想对算法题的求解 贪心策略 动态规划 数据结构中的
|
| 数据结构 |
| 数组 栈与队列 树 图(主要掌握邻接表与邻接矩阵) 并查集 哈希表 |
省赛复盘(侧重讲赛场上的体验)
| 这场省赛可谓惊心又动魄。直接上题目吧。 |
试题 A
题目描述
问题分析
| 签到题,应该学习过python就会 |
代码实现
print("".join(sorted(input())))
试题 B
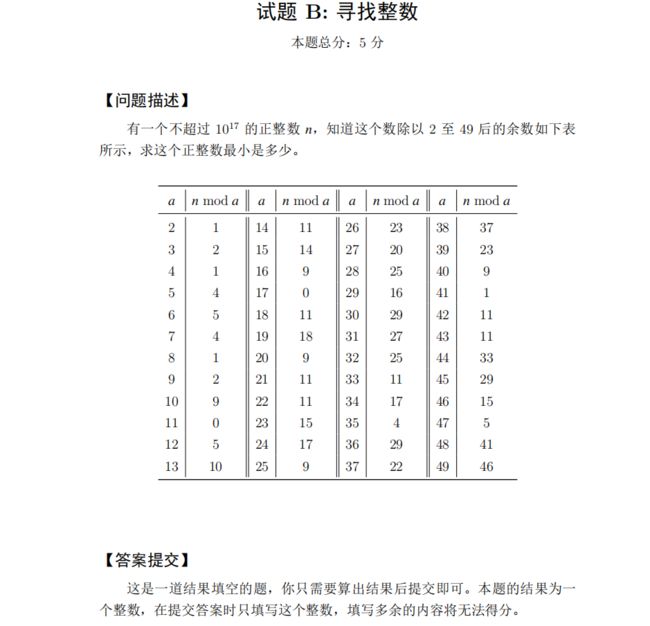
题目描述
问题分析
| 数据量是10^17,非常的大。如果一个一个枚举的话恐怕会枚举到第二天。 在比赛的时候直接中了陷阱,一个一个累加最后真的算了4个小时没有出结果。当时的电脑还差点死机 比赛过后看了几种解题思路如下: 一、加大枚举的步长 二、从1开始枚举,每次枚举到符合除数取余条件之后再进行下一位除数枚举(实现核心如下图) |
| 解释 |
| 11取余2,3,5后余数为1,2,1。 2,3,5的最小公倍数为30。 11+30对2,3,5进行取余之后还是1,2,1 咱们可以根据这个规律对数据进行叠加。 |
代码实现
两种实现方式如下:
由于在赛场上博主没有写出来,在赛后也没有思路于是就参考了别的带来的代码
分别来自大佬:
https://blog.csdn.net/m0_51507437/article/details/124061595
https://blog.csdn.net/ygryth/article/details/124096104?spm=1001.2014.3001.5502
先求步长,再枚举
求步长
i=1
while True:
flag=True
if i%49!=46:
flag=False
if i%48!=41:
flag=False
if i%47!=5:
flag=False
if i%46!=15:
flag=False
if i%45!=29:
flag=False
if flag:
print(i)
i+=1
枚举
mod = [(2, 1), (14, 11), (26, 23), (38, 37),
(3, 2), (15, 14), (27, 20), (39, 23),
(4, 1), (16, 9), (28, 25), (40, 9),
(5, 4), (17, 0), (29, 16), (41, 1),
(6, 5), (18, 11), (30, 29), (42, 11),
(7, 4), (19, 18), (31, 27), (43, 11),
(8, 1), (20, 9), (32, 25), (44, 33),
(9, 2), (21, 11), (33, 11), (45, 29),
(10, 9), (22, 11), (34, 17), (46, 15),
(11, 0), (23, 15), (35, 4), (47, 5),
(12, 5), (24, 17), (36, 29), (48, 41),
(13, 10), (25, 9), (37, 22)]
i = 0
cha = 38137680
while True:
flag = True
num = cha*i+4772009
for x, y in mod:
if num % x != y:
flag = False
break
if flag:
print(num)
break
i += 1
从1开始枚举,每次符合表中除数的取余条件之后再进行下一步枚举
import math
num1=[i for i in range(2,50)] #懒人直接自建数组,不想敲
num2=[1,2,1,4,5,4,1,2,9,0,5,10,11,14,9,0,11,18,9,11,11,15,17,9,23,20,25,16,29,27,25,11,17,4,29,22,37,23,9,1,11,11,33,29,15,5,41,46]
#这里余数很重要啊,一定要一个一个对准来敲,要不然GG
a=True #循环条件
i=0
ans=1
arr=[] #这个数组是存储已经除过的数组(2-49之间的)
#这个函数是求一个数组里面的最小公倍数的,和最小公倍数模版差不多的
def gbs(arr):
k=1
for i in arr:
k=k*i//math.gcd(k,i)
return k
while i<48: #一共就是48个数字嘛,下标是0-47哦,到48就可以停止了
if ans%num1[i]==num2[i]: #判断余数是否相等
arr.append(num1[i]) #相等就存进来
i+=1 #下标+1,继续判断
else:
ans+=gbs(arr) #如果余数不等的话,当前的数字+数组的最小公倍数
print(ans)
试题 C
题目描述
问题分析
| 这个是编程题中的签到题。虽然数据量很小但是当时我还是用的打表法 现在看了看没有这个必要,直接整起就好。 |
代码实现
m,n=1189,841
dic={"A0":0,"A1":1,"A2":2,"A3":3,"A4":4,"A5":5,"A6":6,"A7":7,"A8":8,"A9":9}
v=dic[input()]
for i in range(10):
if n>m:
m,n=n,m
if i==v:
print(m)
print(n)
m//=2
试题 D
题目描述
问题分析
| 有点像桶排序的感觉,桶排序是将不同范围内的数据放在一个桶内,然后对桶内部进行排序 我在赛场上是这么写的,就是先根据数位之和进行排序(入桶),然后在对每个桶进行排序 最后直接遍历输出即可。因为是从1开始向桶内放入数据的,所以每一个桶内默认是排好顺序的 |
代码实现
n=int(input())
m=int(input())
dic={k:[] for k in range(1,55)}
for i in range(1,n+1):
temp=i
anstemp=0
while temp:
anstemp+=temp%10
temp//=10
dic[anstemp].append(i)
ans=[]
for i in dic:
if len(dic[i])!=0:
ans.extend(dic[i])
print(ans[m-1])
试题 E
题目描述
问题分析
| 这个题感觉很难又感觉不难,在赛场上我没有先写这个题。回头看的时候发现真是没有思路。在这里引用一下大佬的代码:大佬的giyhub https://github.com/JohnLulzh2002/My-OJ-exercises |
代码实现
d1,p1,q1,d2,p2,q2=map(int,input().split())
dx1=(-1,-1,0,1,1,0)
dy1=(0,1,1,0,-1,-1)
dx2=(-1,0,1,1,0,-1)
dy2=(0,1,1,0,-1,-1)
dx3=(1,1,0,-1,-1,0)
dy3=(-1,0,1,1,0,-1)
a1=(dx1[d1]*p1+dx1[(d1+2)%6]*q1,dy1[d1]*p1+dy1[(d1+2)%6]*q1)
a2=(dx2[d1]*p1+dx2[(d1+2)%6]*q1,dy2[d1]*p1+dy2[(d1+2)%6]*q1)
a3=(dx3[d1]*p1+dx3[(d1+2)%6]*q1,dy3[d1]*p1+dy3[(d1+2)%6]*q1)
b1=(dx1[d2]*p2+dx1[(d2+2)%6]*q2,dy1[d2]*p2+dy1[(d2+2)%6]*q2)
b2=(dx2[d2]*p2+dx2[(d2+2)%6]*q2,dy2[d2]*p2+dy2[(d2+2)%6]*q2)
b3=(dx3[d2]*p2+dx3[(d2+2)%6]*q2,dy3[d2]*p2+dy3[(d2+2)%6]*q2)
# print(a1,b1)
# print(a2,b2)
# print(a3,b3)
s=[]
s.append(abs(a1[0]-b1[0])+abs(a1[1]-b1[1]))
s.append(abs(a2[0]-b2[0])+abs(a2[1]-b2[1]))
s.append(abs(a3[0]-b3[0])+abs(a3[1]-b3[1]))
print(min(s))
试题 F
题目描述
问题分析
| 当时写这个题的时候我感觉贼简单,于是循环一遍又一遍,最后还是没有把答案给整出来灰常的头疼。 这道题上浪费的时间最长,大概有一个多小时是从10点多写到了将近12点(大家写题的时候可不要这么冒险) 最后实在没办法了就接收了一下字符串直接输出了EMPTY不知道能骗到几分,大家遇见这种情况不要像我一样对一个题软磨硬泡,先把会写的写完,然后再集火不会写的。 |
代码实现
s=input()
for i in range(2**64):
temp=s #temp记录一开始的字符串
tempdelete=set() #集合结构确保边缘字符不重复
for i in range(1,len(s)-1):
if s[i]==s[i-1] and s[i]!=s[i+1]:
tempdelete.add(i)
tempdelete.add(i+1)
if s[i]==s[i+1] and s[i-1]!=s[i]:
tempdelete.add(i-1)
tempdelete.add(i)
s=list(s) #转化成列表方便操作
for i in tempdelete: #删除集合里的边缘字符
s[i]=''
if s==temp:
print(s)
break
if len(s)==0:
print('EMPTY')
break
试题 G
题目描述
问题分析
| 当时考试的时候,我记得有内置的工具库,但是死活想不起来是哪个库了只记得it开头 于是我使用了help()函数查看了内置的英文文档,最后找到了 这么做内存肯定要爆的,我记得在赛场上,我的电脑直接死机了(仅仅测试了20的全排列) 联系工作人员才整好了(上天眷顾我,没有让我电脑直接挂掉,在关机重启的时候程序自己推出去了,所以在这有个教训不要进行超大数据测试 如果电脑重启之后,也许你写的代码什么都没了) 当时的我就希望能够过掉40%的案例不知道最后过掉没有 |
代码实现
我的想法:
import itertools
n=int(input())
l=itertools.permutations(range(1,n+1))
# print(len(list(l)))
l=list(l)
ans=0
for i in l:
for j in range(len(i)):
for k in range(j):
if i[j]>i[k]:
ans+=1
print(ans)
AK代码还是来自上面提到的github那个大佬
n=int(input())
m=998244353
fact=1
ans=[0]
for i in range(1,n+2):
fact*=i
fact%=m
ans.append((ans[-1]*(i+1)+fact*(i+1)*i//2)%m)
print(ans[n-1])
试题 H
题目描述
问题分析
| 我写的时候用的迪杰斯特拉的思想,每次从列表选出一个最大的然后符合条件的操作 操作完之后做出相应的改变。最后得到结果应该能过掉40%的用例 |
代码实现
n,m=map(int,input().split())
ls=[list(map(int,input().split())) for i in range(n)]
for i in ls:
if i[0]%i[1]!=0:
i.append(i[0]//i[1]+1)
else:
i.append(i[0]//i[1])
ans=0
for i in range(m):
tempmax=0
for i in range(len(ls)):
if ls[i][0]>ls[tempmax][0] and ls[i][2]!=0:
tempmax=i
ans+=ls[tempmax][0]
ls[tempmax][0]-=ls[tempmax][1]
ls[tempmax][2]-=1
print(ans)
试题 I
题目描述
问题分析
| 剩下这两个直接给我整麻了 |
代码实现
等待大佬的题解。。。。。。
试题 J
题目描述
问题分析
| 剩下这两个直接给我整麻了 |
代码实现
等待大佬的题解。。。。
总结
| 一套操作下来我得到的预估也就40-50分,加上混的分数估计封顶60。但是在省赛800人中取得了30多名的成绩,由此看来蓝桥杯还是好拿奖的,只要你认真对待每一个细节。通过备赛我掌握了原本我不可能主动去掌握的基础算法知识。我也真心的介意大家有时间、有机会了可以参加一下蓝桥杯。对于国赛的话我想我会去参加,也会去积极备赛。如果取得好的成绩我还会给大家分享一下备赛经历会还会对比赛进行复盘。最后如果大家在蓝桥杯中获奖之后不要太高兴,得意忘形,如果没有获奖应该认真总结,好好反思。祝大家都能取得一个让自己的满意的成绩。 |