基于 Java 机器学习自学笔记 (第61-62天:ID3决策树)
注意:本篇为50天后的Java自学笔记扩充,内容不再是基础数据结构内容而是机器学习中的各种经典算法。这部分博客更侧重于笔记以方便自己的理解,自我知识的输出明显减少,若有错误欢迎指正!
目录
一、关于决策树的历史
二、关于一些知识记录
· 熵与信息增益
三、代码需要的数据分析
四、代码准备——基本函数
4.1 根构造函数
4.2 简单投票选定标签
4.3 判纯
4.4 选择最佳的条件属性列
4.5 计算条件熵
五、树的创建与分割属性集
5.1 属性集分割
5.2 树的构建与非根构造函数
六、通过决策树实现数据分类
七、数据测试
一、关于决策树的历史
最初的决策树算法是心理学家兼计算机科学家E.B.Hunt 1962年在研究人类的概念学习过程时提出的CLS(Concept Learning System),这个算法确立了决策树“分而治之”的学习策略。罗斯·昆兰在Hunt的指导下于1968年在美国华盛顿大学获得计算机博士学位,然后到悉尼大学任教。1978年他在学术假时到斯坦福大学访问,在一门研究生课程上要求写一个程序来学习出完备正确的规则,以判断国际象棋残局中一方是否会在两步棋后被将死。昆兰写了一个类似于CLS的程序。其中最重要的改进是引入了信息增益准则,后来他把这个工作整理出来在1979年发表,这就是ID3算法。
1986年昆兰应邀在Machine Learning创刊号上重新发表了ID3算法,掀起了决策树研究的热潮,短短几年间众多决策树算法问世,ID4,ID5等名字迅速被其他研究者提出的算法占用,昆兰只好将自己的ID3后续算法命名为C4.0(Classifer 4.0),在此基础上进一步提出了著名的C4.5(只是对C4.0做了些小改进),将后续的商业化版本称为C5.0。
二、关于一些知识记录
来源于:决策树快问快答_闵帆的博客-CSDN博客
1.决策树是为决策而构建的树,它是人类知识的一种体现,因此具有天然的可解释性优势。我的理解是,它一种将选择全部枚举出来,并且组合一系列选择最终导向结构的一颗树形结构。比如下面这个买房放款决策:
2.决策的获得方式可以通过固有的知识准备,也可以通过经验得到,这个是我们生活的常识,我们永远不知道我们未来的道路上会面临什么抉择,所以我们可以通过提前了解可能的知识去提前未雨绸缪,或者结合我们曾经的“经验”,从而在面对抉择时做出“临时”的选择。
而我们机器学习中的学习,往往都是通过实际的数据中学习,而并非一个先前给定的一个大框架。比如,二叉查询树就像事先通过 “ 固有的知识准备 ” 构建出来的已知的决策树,然后在之后遇到需要查询的数据时直接“ 套用 ”就好了。而广义的机器学习中的决策树就像通过经验,在面对决策时临时进行构建“ 分支 ”,设计出针对当前问题的一种决策分类。
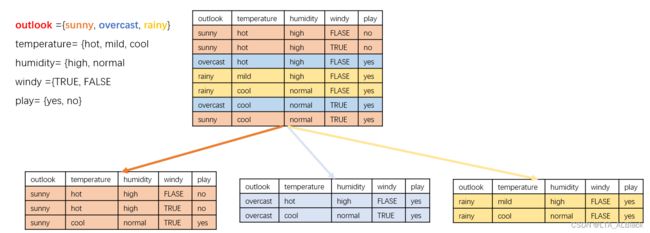
3.决策树算法的核心在于采用何种数据类型去进行分割,例如我们下面属性的weather数据集,我们确定一种条件类别(下图我们选择outlook条件类别),然后即可按照这种条件的分类分别选定当前根的若干孩子:
而这里进行属性选择的依据就是看这个条件是否可以将数据分得足够“ Pure ”(这个过程又可以说是“ 特征选择 ”,即选取对训练数据具有分类能力的特征),这里判断是否“ Pure ”需要基于某些启发式的规则:针对离散属性的信息增益、针对连续属性的信息增益率、基尼指数。
一个数据如果不够“ Pure ”,那么它就是相对应的“ Chaos ”(或说选择这个特征是没有分类能力的)。当我们按照某个标准分类的时候,每个类别都有比较独立的内聚时,最大可能实现了两个数据非A即B,那么这个分类就是“ Pure ”的。但是现实生活中有些东西我们很难说的很绝对,这就就导致我们可以没法一次就能非得我们所要求的“ Pure ”,所以只得再分。
一般来说,决策树的ID3算法选用的就是信息增益的方法去分割数据,它的效果非常优秀,能在绝大多数情况下获得叶子节点最少的、最小的决策树,所谓叶子节点最少也就表示最后我们的决策的针对性越强。所以我们下文会具体介绍信息增益这个方法。
4.决策树越小越好。树的分叉越少(if-else越少),这颗树在新的实例上方法的适用性就越强,就如图奥卡姆剃刀定理那般。若树的分叉非常庞大,结构极其复杂,那么这颗树就偏向过拟合,其适应性和扩展性就会变弱。面对这种情况我们会采用剪枝去让树尽可能地小,从而牺牲精度,提高泛化的特性。这个过程中我可以先构造一个足够庞大的决策树再剪枝(后剪枝),或者在构造过程中剪枝(前剪枝)
奥卡姆剃刀定律:“如无必要,勿增实体”,即“简单有效原理”。知识表达约简练,那么他的扩展性、延伸性就更强,能更好地结合各种问题从而有专门化的发展。
过拟合:随着训练过程的进行,模型复杂度不断变大,在训练集上的错误渐渐减小。可是在验证集上的错误却反而渐渐增大——即由于训练出来的网络过拟合了训练集,对训练集以外的数据却不work。
5.决策树是信息模型的构建,一般来说,对于一个数据集一旦够着了良好的数据,那个原始数据结构就可以不采用而直接使用学习好的模型。这种基于训练构建的模型往往非常花费时间,但是相对获得的收益是——测试会很快。
· 熵与信息增益
熵(Entropy)这个概念我们在中学的化学中早有耳闻,它代表着物质的混乱程度(气体>液体>固体),但是在信息领域略有差异。在信息论与概率统计中,熵表示随机变量不确定性的度量。可见虽然描述事物缩小了,但是依旧是对于混乱度的度量。
设\(X\)是一个取有限个值的离散随机变量,其概率分布为:\[P\left\{X=x_{i}\right\}=p_{i}, \quad i=1,2 \cdots, n\] 那么我们可以定义关于\(X\)的熵定义有\[H(X)=-\sum_{i=1}^{n} p_{i} \log p_{i}\] 这个熵的定义式只依赖于\(X\)的分布,而与\(X\)的取值无关,所以也可将X的熵记作\(H(p)\)
注意:在上式中的对数以2为底或以自然对数e为底对应了不同的单位:
- 对数以2为底的单位称作比特(Bit)
- 对数以e为底的单位称之为纳特(Nat)
更多细节不赘述,在这篇文章中有关于信息熵更多细节的描述,其中有关于二元信息熵的一个证明,简单来说,当随机变量只有0/1的二元取值时,有这样的分布\[P(X=1)=p, \quad P(X=0)=1-p, \quad 0 \leq p \leq 1\] 这是如果\(p=1.0\)或\(p=0.0\)那么熵最小,数据的不定性(混乱度)最小,反之当\(p=0.5\)时不定性(混乱度)最大。这个也好理解,若一个掷硬币的两面都是同一个花纹,那么最后结果出现什么样花纹的可能性恒定地稳定,完全不混乱;反之两面花纹不一样,最后结果就不再那么可靠稳定,各种可能性参半。这可以理解是信息邻域的“ 熵增 ”了。
另外再引入条件熵的概念,条件熵(conditional entropy)\(H ( Y ∣ X )\)表示在已知随机变量\(X\)的条件下随机变量\(Y\)的不确定性,定义为\(X\)给定条件下\(Y\)的条件概率分布的熵对\(X\)的数学期望:\[H(X \mid Y)=\sum_{i=1}^{n} p_{i} H\left(Y \mid X=x_{i}\right)\] 其中\(p_{i}=P\left(X=x_{i}\right), i=1,2, \cdots, n\)。至此,我们就可以提出信息增益的概念了:
信息增益(Information Gain),即已知特征X的信息可以帮助Y的信息不确定性减少的程度。
特征\(A\)对训练数据集\(D\)的信息增益\(g(D,A)\),定义为集合\(D\)的经验熵\(H(D)\)与特征\(A\)给定条件下\(D\)的经验条件熵\(H(D∣A)\)之差,即:\[g(D,A)=H(D)−H(D∣A)\] 这里的特征值\(A\)的不同,会对数据集\(D\)照成不同的影响,有的大有的小,造成的影响越大其信息增益也就越大,也就有更强的分类能力。所以在每次选取最合适的条件类(可以视为特征\(A\))时我们都要计算这个条件类相对于训练集\(D\)的信息增益\(g(D,A)\),并多次计算选取最大的那个作为我们的核心选择条件类!
三、代码需要的数据分析
/**
* The data.
*/
Instances dataset;
/**
* Is this dataset pure (only one label)?
*/
boolean pure;
/**
* The number of classes. For binary classification it is 2.
*/
int numClasses;
/**
* Available instances. Other instances do not belong this branch.
*/
int[] availableInstances;
/**
* Available attributes. Other attributes have been selected in the path
* from the root.
*/
int[] availableAttributes;- 数据集
- 纯度判定,用来权衡我们采用某些属性条件划分之后(或者没划分)数据是否是“ Pure ”的,对于Pure(纯了)的数据,为了控制树的大小(或者理论上没法再分),我们将停止分叉。这里我们通过判断一个数据内的标签差异程度来判断Pure,这里我们认为若一颗子树内只有一个标签了,那么就认为足够Pure了。
- numClasses决断列的熟悉数目,因为play = {yes, no},故值为2
- availableInstances存储当前还可在分的数据集下标,其长度随着可分的数据行下标个数变化而变化
- availableAttributes当前还可用的条件属性对应的下标集,其长度随着可分的条件属性的个数变化而变化(从这里可以窥见,我们把条件属性量化了)
/**
* The selected attribute.
*/
int splitAttribute;
/**
* The children nodes.
*/
ID3[] children;
/**
* My label. Inner nodes also have a label. For example, never appear in the training data, but
* is valid in other cases.
*/
int label;
/**
* The prediction, including queried and predicted labels.
*/
int[] predicts;
/**
* Small block cannot be split further.
*/
static int smallBlockThreshold = 3; - 选为当前进行分类目标的条件属性类(已量化,故用int)
- 孩子指针(引用)数组。对于非确定N叉数的孩子表示,统一采用在每个树结点中放入一个指针数组,分别指向其每个孩子。这个树状数据结构的基本内容,不赘述
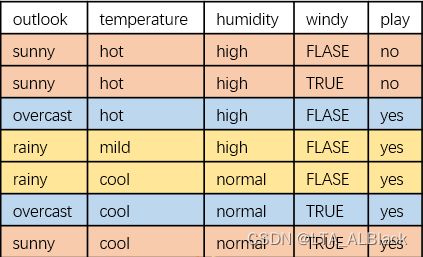
- label,记录结点最多的决策列属性(标签)下标。比如下图中,有5个yes,2个no,因为yes顺序放于第1个,因此下标为0,故label=0
- predicts数组
- smallBlockThreshold是一个最低的限度,若当前结点内的数据项低于或等于这个阈值就不再分,这是控制决策树大小的一个变量
四、代码准备——基本函数
4.1 根构造函数
/**
********************
* The constructor.
*
* @param paraFilename
* The given file.
********************
*/
public ID3(String paraFilename) {
dataset = null;
try {
FileReader fileReader = new FileReader(paraFilename);
dataset = new Instances(fileReader);
fileReader.close();
} catch (Exception ee) {
System.out.println("Cannot read the file: " + paraFilename + "\r\n" + ee);
System.exit(0);
} // Of try
dataset.setClassIndex(dataset.numAttributes() - 1);
numClasses = dataset.classAttribute().numValues();
availableInstances = new int[dataset.numInstances()];
for (int i = 0; i < availableInstances.length; i++) {
availableInstances[i] = i;
} // Of for i
availableAttributes = new int[dataset.numAttributes() - 1];
for (int i = 0; i < availableAttributes.length; i++) {
availableAttributes[i] = i;
} // Of for i
// Initialize.
children = null;
// Determine the label by simple voting.
label = getMajorityClass(availableInstances);
// Determine whether or not it is pure.
pure = pureJudge(availableInstances);
}// Of the first constructor
依次为读取数据->设置决策类->读取决策类的属性个数与numClasses->初始化availableInstances->初始化availableAttributes->初始化后续属性
这里初始化里面用到两个函数,下面简单介绍下
4.2 简单投票选定标签
/**
**********************************
* Compute the majority class of the given block for voting.
*
* @param paraBlock
* The block.
* @return The majority class.
**********************************
*/
public int getMajorityClass(int[] paraBlock) {
int[] tempClassCounts = new int[dataset.numClasses()];
for (int i = 0; i < paraBlock.length; i++) {
tempClassCounts[(int) dataset.instance(paraBlock[i]).classValue()]++;
} // Of for i
int resultMajorityClass = -1;
int tempMaxCount = -1;
for (int i = 0; i < tempClassCounts.length; i++) {
if (tempMaxCount < tempClassCounts[i]) {
resultMajorityClass = i;
tempMaxCount = tempClassCounts[i];
} // Of if
} // Of for i
return resultMajorityClass;
}// Of getMajorityClass临时构造一个 “统计决策列所有可能类别” 的数组tempClassCounts ,然后投票选择最多决策类别。决策类别有一个我们熟悉的称为——标签(天气数据中的play决策的yes与no,这里就有两个标签yes/no)
4.3 判纯
/**
**********************************
* Is the given block pure?
*
* @param paraBlock
* The block.
* @return True if pure.
**********************************
*/
public boolean pureJudge(int[] paraBlock) {
pure = true;
for (int i = 1; i < paraBlock.length; i++) {
if (dataset.instance(paraBlock[i]).classValue() != dataset.instance(paraBlock[0])
.classValue()) {
pure = false;
break;
} // Of if
} // Of for i
return pure;
}// Of pureJudge“ 若一颗子树内只有一个标签了,那么就认为足够Pure了 ”这个是我刚刚介绍Pure变量用的语言,这里就是实现我这句话而已。变量全部可用数据行,看大家的标签是不是与第一个数据行的标签一致。
4.4 选择最佳的条件属性列
我最开始介绍决策树时提到了 “ 一般来说,决策树的ID3算法选用的就是信息增益的方法去分割数据 ”于是,这里代码便不难理解了,分别遍历所有条件属性,计算条件属性\(A_i\)对训练数据集\(D\)的最大信息增益\(\underset{0 \leq i < n}{\max }{g(D,A_i)}\)。
同时\(g(D,A)=H(D)−H(D∣A)\),而\(H(D)\)是固定的,这样的话有下面的基本推导:\[\underset{0 \leq i < n}{\arg \max }{g(D,A_i)} = \underset{0 \leq i < n}{\arg \max } \left ( H(D)-H(D|A_{i}) \right ) = \underset{0 \leq i < n}{\arg \max }\left ( -H(D|A_{i}) \right ) = \underset{0 \leq i < n}{\arg \min } H(D|A_{i})\] 如此,下面的代码便不难理解了。
/**
**********************************
* Select the best attribute.
*
* @return The best attribute index.
**********************************
*/
public int selectBestAttribute() {
splitAttribute = -1;
double tempMinimalEntropy = 10000;
double tempEntropy;
for (int i = 0; i < availableAttributes.length; i++) {
tempEntropy = conditionalEntropy(availableAttributes[i]);
if (tempMinimalEntropy > tempEntropy) {
tempMinimalEntropy = tempEntropy;
splitAttribute = availableAttributes[i];
} // Of if
} // Of for i
return splitAttribute;
}// Of selectBestAttribute4.5 计算条件熵
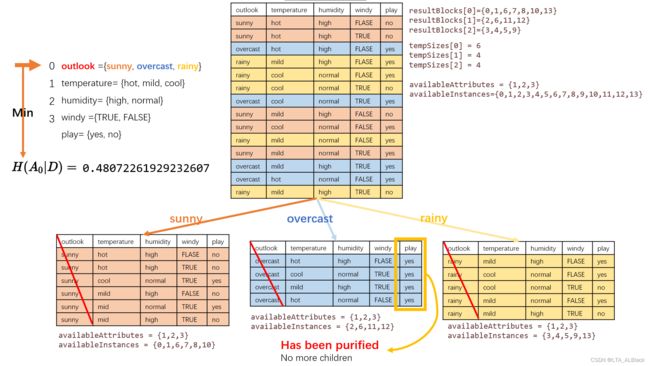
刚刚我们给出了条件熵的概率以及公式,这里为与代码对照,再度展示出公式:\[H(X \mid Y)=\sum_{i=1}^{n} p_{i} H\left(Y \mid X=x_{i}\right)\] 这里有\(p_{i}=P\left(X=x_{i}\right), i=1,2, \cdots, n\)。这里的\(x_{i}\)表示每个条件属性列环境下具有的类别数目,比如对于\(X=temperature\),就有\(\{x_{0} = hot,x_{1} = mild,x_{2} = cool\}\),而\(p_i\)就表示\(x_i\)在当前整列当中出现的概率,假如说数据集中有7行数据行,hot的天气有3天,那么自然\(p_{i} = \frac{3}{7}\)。而\(H\left(Y \mid X=x_{i}\right)\)直接套入熵的计算公式就好了。具体由下图这样的例子:
这个图当中,我们假定了\(A_{1} = temperature\)的情况下,\(A_{1}\)相对于有7行数据的数据集\(D\)的信息熵计算过程。这个图下面我们算了一系列的\(H(Y|X=x_{i})\),最终加起来就好了。这里为了方便编写代码,我们建立了一个以 条件属性类型数 * 标签个数 的二维矩阵用来统计 内部的\(p_{i}\)。这个内部的\(p_{i}\)不同于外部的\(p_{i}\),内部这\(p_{i}\)的分母是条件属性中类别的总数,而分子是在这样限制下标签的个数。例如对于天气为hot的天气中,yes标签概率为\(\frac{1}{3}\);no标签概率为\(\frac{2}{3}\)
(注:上图为简化,所有的\(\log\)计算都是以2为底的)
/**
**********************************
* Compute the conditional entropy of an attribute.
*
* @param paraAttribute
* The given attribute.
*
* @return The entropy.
**********************************
*/
public double conditionalEntropy(int paraAttribute) {
// Step 1. Statistics.
int tempNumClasses = dataset.numClasses();
int tempNumValues = dataset.attribute(paraAttribute).numValues();
int tempNumInstances = availableInstances.length;
double[] tempValueCounts = new double[tempNumValues];
double[][] tempCountMatrix = new double[tempNumValues][tempNumClasses];
int tempClass, tempValue;
for (int i = 0; i < tempNumInstances; i++) {
tempClass = (int) dataset.instance(availableInstances[i]).classValue();
tempValue = (int) dataset.instance(availableInstances[i]).value(paraAttribute);
tempValueCounts[tempValue]++;
tempCountMatrix[tempValue][tempClass]++;
} // Of for i
// Step 2.
double resultEntropy = 0;
double tempEntropy, tempFraction;
for (int i = 0; i < tempNumValues; i++) {
if (tempValueCounts[i] == 0) {
continue;
} // Of if
tempEntropy = 0;
for (int j = 0; j < tempNumClasses; j++) {
tempFraction = tempCountMatrix[i][j] / tempValueCounts[i];
if (tempFraction == 0) {
continue;
} // Of if
tempEntropy += -tempFraction * Math.log(tempFraction);
} // Of for j
resultEntropy += tempValueCounts[i] / tempNumInstances * tempEntropy;
} // Of for i
return resultEntropy;
}// Of conditionalEntropy五、树的创建与分割属性集
5.1 属性集分割
/**
**********************************
* Split the data according to the given attribute.
*
* @return The blocks.
**********************************
*/
public int[][] splitData(int paraAttribute) {
int tempNumValues = dataset.attribute(paraAttribute).numValues();
// System.out.println("Dataset " + dataset + "\r\n");
// System.out.println("Attribute " + paraAttribute + " has " +
// tempNumValues + " values.\r\n");
int[][] resultBlocks = new int[tempNumValues][];
int[] tempSizes = new int[tempNumValues];
// First scan to count the size of each block.
int tempValue;
for (int i = 0; i < availableInstances.length; i++) {
tempValue = (int) dataset.instance(availableInstances[i]).value(paraAttribute);
tempSizes[tempValue]++;
} // Of for i
// Allocate space.
for (int i = 0; i < tempNumValues; i++) {
resultBlocks[i] = new int[tempSizes[i]];
} // Of for i
// Second scan to fill.
Arrays.fill(tempSizes, 0);
for (int i = 0; i < availableInstances.length; i++) {
tempValue = (int) dataset.instance(availableInstances[i]).value(paraAttribute);
// Copy data.
resultBlocks[tempValue][tempSizes[tempValue]] = availableInstances[i];
tempSizes[tempValue]++;
} // Of for i
return resultBlocks;
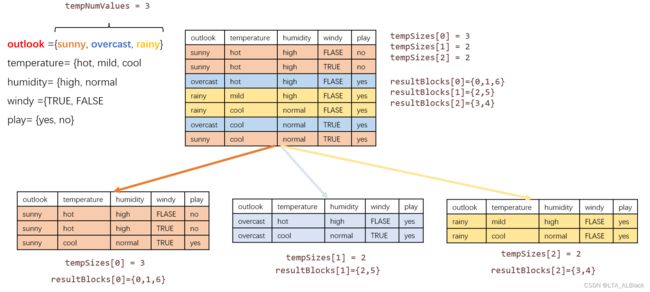
}// Of splitData这个分割操作可以用一个图来很好诠释:
最开始我们的数据集是{0,1,2,3,4,5,6},然后我们发现当前最好的分割属性是temperature,于是关注于temperature列,通过这一列不同,将数据分割为三块{{0,1,6},{2,5},{3,4}}。具体代码就不赘述了,如果理解有点困难的话,记住,这里tempSizes最开始的功能是统计每块的数目以方便后面给resultBlocks的二维分配空间;后面tempSizes之所以清空了是因为后面tempSize的作用是拷贝指针。
5.2 树的构建与非根构造函数
树的创建过程中我们使用了递归创建的思路,因此每个结点的创建代码我们都需要留有一个出口。结合以往DFS的经验,这个出口无疑在代码开头,具体来说,两个出口:
- 当前结点Pure吗?(当前结点的所有数据行的标签是否一致)
- 当前结点的数据行是否已经≤阈值了?
假如说,数据已经小于阈值了,不会再分割了,但是这个数据集内的数据集并不纯,即还有多个标签怎么办呢?这个时候就可以采用投票的策略权值最多的标签。这就是为什么我要构造 简单投票选定标签 函数getMajorityClass。
之后14~16行完成了最佳条件属性列的选取,同时分割除了这个属性类引导新数据集下标集合;同时分配的孩子指针(引用)数组空间(记住,这里只是指针空间)
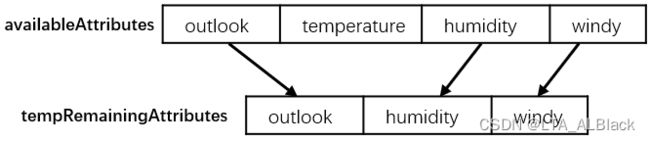
18~26行代码是构造新的一个数组tempRemainingAttribute,这个数组其实就是把排除splitAttribute属性列的原属性数组availableAttribute拷贝了下来:
这么做的目的是希望遗传给下一代时不要选择这个已经选过的属性列
28~41行就是创建分配孩子的实际空间的代码,每个结点在分配实际空间时都会调用构造函数,同时也会因为构造函数参数调入的差异触发不同的构造函数。这里代码中巧妙利用了构造函数的重载,使得每个子节点的构造函数调用的方式与根节点略有差异。这个差异主要在于dataset、availableInstances、availableAttributes这三个参数的获取途径:
- 根节点的dataset是从读文件获取的;非根节点继承于其父亲
- 根节点availableInstances是用availableInstances[i]=i读取的全数据集的行下标;非根节点的availableInstances是来自其父亲分割的tempSubBlocks的一部分
- 根节点availableAttributes是用availableAttributes[i]=i读取的全数据集的条件属性列下标;非根节点的availableInstances是来自其父亲抛弃了某些列的原availableAttributes
这部在分孩子的时候要注意,按照条件属性splitAttribute进行分叉的时候,有时虽然splitAttribute属性的某些类并没有数据,但是我们还是会默认分与这个条件属性包含的类数目相同的指针数目。因此要格外注意空孩子问题(30~31行)
/**
**********************************
* Build the tree recursively.
**********************************
*/
public void buildTree() {
if (pureJudge(availableInstances)) {
return;
} // Of if
if (availableInstances.length <= smallBlockThreshold) {
return;
} // Of if
selectBestAttribute();
int[][] tempSubBlocks = splitData(splitAttribute);
children = new ID3[tempSubBlocks.length];
// Construct the remaining attribute set.
int[] tempRemainingAttributes = new int[availableAttributes.length - 1];
for (int i = 0; i < availableAttributes.length; i++) {
if (availableAttributes[i] < splitAttribute) {
tempRemainingAttributes[i] = availableAttributes[i];
} else if (availableAttributes[i] > splitAttribute) {
tempRemainingAttributes[i - 1] = availableAttributes[i];
} // Of if
} // Of for i
// Construct children.
for (int i = 0; i < children.length; i++) {
if ((tempSubBlocks[i] == null) || (tempSubBlocks[i].length == 0)) {
children[i] = null;
continue;
} else {
// System.out.println("Building children #" + i + " with
// instances " + Arrays.toString(tempSubBlocks[i]));
children[i] = new ID3(dataset, tempSubBlocks[i], tempRemainingAttributes);
// Important code: do this recursively
children[i].buildTree();
} // Of if
} // Of for i
}// Of buildTree
/**
********************
* The constructor.
*
* @param paraDataset
* The given dataset.
********************
*/
public ID3(Instances paraDataset, int[] paraAvailableInstances, int[] paraAvailableAttributes) {
// Copy its reference instead of clone the availableInstances.
dataset = paraDataset;
availableInstances = paraAvailableInstances;
availableAttributes = paraAvailableAttributes;
// Initialize.
children = null;
// Determine the label by simple voting.
label = getMajorityClass(availableInstances);
// Determine whether or not it is pure.
pure = pureJudge(availableInstances);
}// Of the second constructor为了更加生动展现,我这里列出了weather.arff数据的决策树的全过程(爆肝啊....(≧口≦))
数据集:
@relation weather.symbolic
@attribute outlook {sunny, overcast, rainy}
@attribute temperature {hot, mild, cool}
@attribute humidity {high, normal}
@attribute windy {TRUE, FALSE}
@attribute play {yes, no}
@data
sunny,hot,high,FALSE,no
sunny,hot,high,TRUE,no
overcast,hot,high,FALSE,yes
rainy,mild,high,FALSE,yes
rainy,cool,normal,FALSE,yes
rainy,cool,normal,TRUE,no
overcast,cool,normal,TRUE,yes
sunny,mild,high,FALSE,no
sunny,cool,normal,FALSE,yes
rainy,mild,normal,FALSE,yes
sunny,mild,normal,TRUE,yes
overcast,mild,high,TRUE,yes
overcast,hot,normal,FALSE,yes
rainy,mild,high,TRUE,no
根分出通过length(outlook) = 3 从而分出了三颗子树,其中第二颗子树是纯的
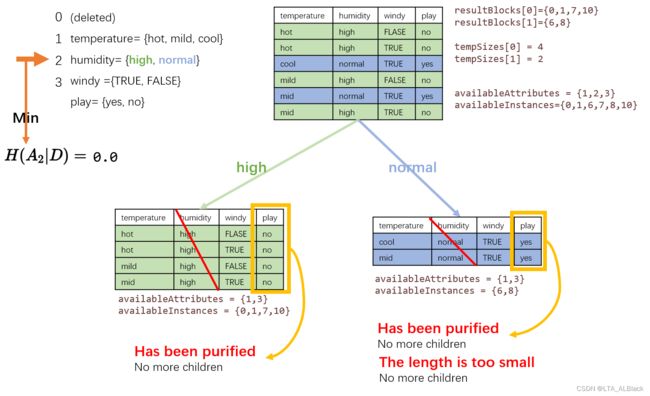
第一颗子树的再分化情况:
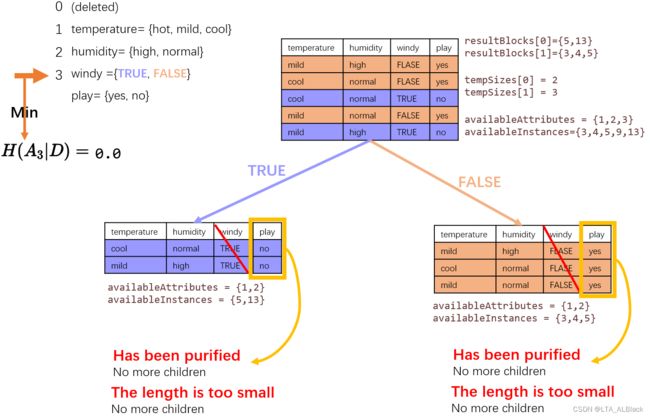
第三颗子树的再分化情况:
六、通过决策树实现数据分类
我们这里采用的是基于自己的数据进行分类,因此准确度可以保证是1.0
因此代码主要还是示范怎么通过决策树去查看这个数据最终的归属,或者说这个数据的标签应该是什么。
classifiy( )函数的形参一个数据行,树的每层分别判断这个数据基于某个条件属性的某列,并且通过每次判断的结果,使得搜索逐步向下,直到遇到某个决策。
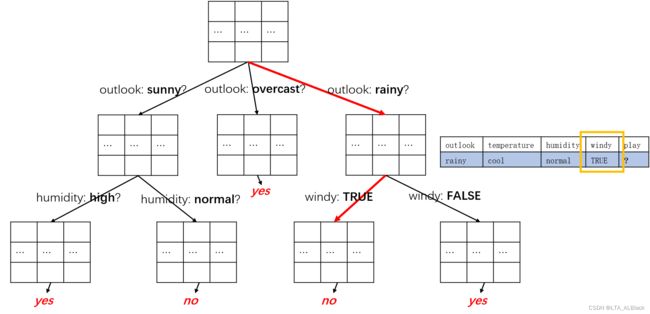
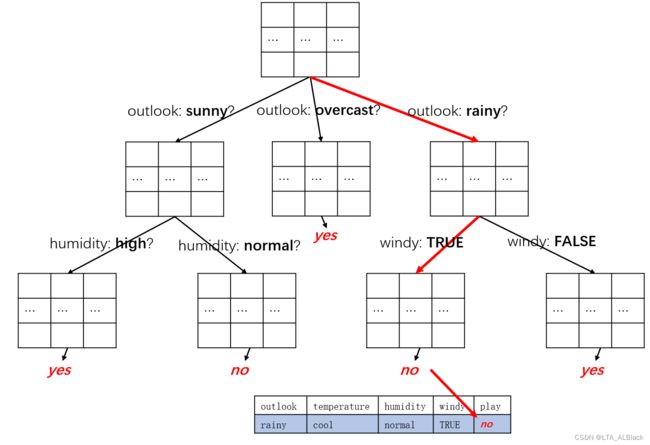
下面我将我刚刚得到的决策树简化,然后逐步分析这个数据行:
- 首先要判断当前结点是否有孩子,如果没有孩子的话说明结点已然是终端结点,那么通过简单投票选取可能的标签(投票已经通过构造函数内的接口运行,结构存放在label中)
- 若有孩子,那么取出这个结点当时在建树时选择的划分条件属性,因为后续的分叉是基于这个条件属性的,后续我们的分类数据要继续向下深入搜索的话,模仿原来的分叉路径是必须的。
- 若已经发现分叉,但是孩子是空的,这种情况往往是因为在分叉时已经给孩子分配了空间,但是在基于条件属性进行划分时这部分并没有类别记录。遇到这种情况默认为没有这个孩子,按照第1步方案执行。
/**
**********************************
* Classify an instance.
*
* @param paraInstance
* The given instance.
* @return The prediction.
**********************************
*/
public int classify(Instance paraInstance) {
if (children == null) {
return label;
} // Of if
ID3 tempChild = children[(int) paraInstance.value(splitAttribute)];
if (tempChild == null) {
return label;
} // Of if
return tempChild.classify(paraInstance);
}// Of classify
/**
**********************************
* Test on a testing set.
*
* @param paraDataset
* The given testing data.
* @return The accuracy.
**********************************
*/
public double test(Instances paraDataset) {
double tempCorrect = 0;
for (int i = 0; i < paraDataset.numInstances(); i++) {
if (classify(paraDataset.instance(i)) == (int) paraDataset.instance(i).classValue()) {
tempCorrect++;
} // Of i
} // Of for i
return tempCorrect / paraDataset.numInstances();
}// Of test七、数据测试
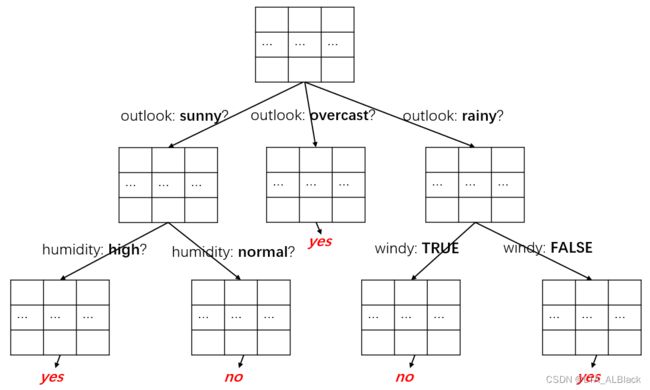
数据测试的方式是自我训练建立模型,同时自我核对相似度。因为测试数据源于同一个模型,所以识别率绝对是1.0。那么为了验证代码的正确性,我们就对这颗树进行一次前序遍历(DFS),最后将测试结果同我上面(花大量时间)画的图进行比对即可。
/**
**********************************
* Test on the training set.
*
* @return The accuracy.
**********************************
*/
public double selfTest() {
return test(dataset);
}// Of selfTest
/**
*******************
* Overrides the method claimed in Object.
*
* @return The tree structure.
*******************
*/
public String toString() {
String resultString = "";
String tempAttributeName = dataset.attribute(splitAttribute).name();
if (children == null) {
resultString += "class = " + label;
} else {
for (int i = 0; i < children.length; i++) {
if (children[i] == null) {
resultString += tempAttributeName + " = "
+ dataset.attribute(splitAttribute).value(i) + "\n" + "class = " + label;
} else {
resultString += tempAttributeName + " = "
+ dataset.attribute(splitAttribute).value(i) + "\n" + children[i]
+ "\n";
} // Of if
} // Of for i
} // Of if
return resultString;
}// Of toString
/**
*************************
* Test this class.
*
* @param args
* Not used now.
*************************
*/
public static void id3Test() {
ID3 tempID3 = new ID3("D:/Java DataSet/weather.arff");
// ID3 tempID3 = new ID3("D:/data/mushroom.arff");
ID3.smallBlockThreshold = 3;
tempID3.buildTree();
System.out.println("The tree is: \r\n" + tempID3);
double tempAccuracy = tempID3.selfTest();
System.out.println("The accuracy is: " + tempAccuracy);
}// Of id3Test
/**
*************************
* Test this class.
*
* @param args
* Not used now.
*************************
*/
public static void main(String[] args) {
id3Test();
}// Of main(今天的内容挺多的,今天写了一天了,结尾就不再过度分析了...后续关于决策树的更新也会基于这篇博客后方添加)