3.机器学习—数据科学包3.4Matplotlib

一.课程简介和环境搭建

1.数据分析—进阶技能树

1. 懂基本的涉及理论，会简单的数据分析
2. 懂得用建模、可视化方法对数据进行探索和总结(股票K线图）
3. 深入相关业务，利用数据分析直接创造价值（如投资策略，个性化推荐）

2.matplotlib简介

1. matplotlib是基于Python语言的开源项目，是python的一个数据绘图包，用户在熟悉了核心对象之后，可以轻易地定制对象。
2. 函数式绘图和面向对象式绘图

• 函数式绘图，参考了matlab里面地绘图函数语法
• 面向对象式绘图，matplotlib的底层架构，有更多功能。

3.环境搭建

1. 使用Anaconda作为核心解释器和相关的包。
   Anaconda集成了数据分析，科学计算相关的几乎所有包。
   比如：Numpy，Scipy，Matplotlib,Ipython
2. Pycharm作为IDE，也就是编辑器的功能。
   community版本式免费的。
   Python console用的是Ipython。

二.Numpy简介

1.Numpy是什么

• Numpy是Python的开源的数值计算扩展
• 可用来存储和处理大型矩阵，比Python自身数据结构要高效
• Numpy将Python变成一种免费的强大的Matlab系统

其实python本身有数据结构

• 比如说用嵌套的l矩阵就可以存储矩阵，但是numpy比python自身的数据结构更高效。也就是Numpy将Python变成一种免费的强大的Matlab系统。

2.ndarray

ndarray可以理解为一个矩阵，相当于存储了一些我们需要的数据。

2.1创建nadarray对象

1. 从Python的基础数据对象直接转化过来
   
2. 用Numpy内生的函数生成
   
3. 从磁盘中读取数据：2种—从文件种读取和从数据库种读取
   这里是从文件中读取

x=np.loadtxt('000001.csv',delimiter=',',skiprows=1,usecols=(1,4,6),unpack=False)
# delimiter，定界符，分隔符，分界符。skiprow，跳行(由于第一行不是数据，所以要跳过)。usecol,用哪几列。unpack,不把导入的这些放到一个array里面，放到不通过array里面。
x
x.shape

# unpack=True，将数据放到不同array中
x=np.loadtxt('000001.csv',delimiter=',',skiprows=1,usecols=(1,4,6),unpack=True)
open
open.shape

2.2ndarray基本操作

1. ndarray的四则运算
2. 索引和切片
   python中索引都是从0开始

# 与python操作相同
print c[1:5]
print c[:5]
print c[5:]
# 加上步长
print c[::-1]

3. 常用函数
   统计函数
   min，max，median，mean，variance,sort
   调用函数方法

• np.func(x) ()中是nparray对象
• x.func() x是nparray对象
  使用sort()要注意
  sort(x)排序之后生成新的数组，而这个数组是排了序的，原来的x没变化
  x.sort() 排序之后x变化为排序后的x。

import numpy as np

c=np.random.randint(1,100,10)
c_sort=np.sort(c)
print(c_sort) # 有值，说明生成了新的array
print(c.sort())# None，无值，说明没成新的array。原来的araay发生变化
print(c)

4. 实践

import numpy as np

x=np.random.randint(1,100,10)

np.savetxt('testfile.txt',x) #保存x到文件testfile.txt中

c=np.loadtxt('testfile.txt') #凑够文件导入数据

c_sort=np.sort(c)

highest=np.max(c)
lowest=np.min(c)
mean=np.mean(c)

三.散点图

• 散点图显示两组数据的值，每个点的坐标位置由变量的值决定
• 由一组不连接的点完成，用于观察两种变量的相关性
• 例如身高–体重、温度–维度、等。
• 用来探究两个对象的相关性，相关性三种情况：正相关，负相关、不相关

1.举例说明

import numpy as np
import matplotlib.pyplot as plt

height=[161,170,182,175,173,165]
weight=[50,58,80,70,69,55]

plt.scatter(height,weight) #hegiht是x轴，weight是y轴

plt.show()

2. 不相关

import numpy as np
import matplotlib.pyplot as plt

N=1000
x=np.random.randn(N)
y1=np.random.randn(len(x))

plt.scatter(x,y1)

plt.show()

3. 正相关

N=1000
x=np.random.randn(N)
y=x+np.random.randn(N)*0.5

plt.scatter(x,y1)

plt.show()

负相关就是在y那里加上一个负号。

4. 股票实例

# 读取表中的开盘价open和收盘价close，分别读到连个array中
open,close=np.loadtxt('000001.csv',delimiter=',',skiprows=1,usecols=(1,4),unpack=True)

change=close-open #每日开盘价和收盘价之间的差价

yesterday=change[:-1] #取第一个值到倒数第二个值。前一天的价格涨幅序列
today=change[1:] # 取第二个值到最后一个值。后一天的价值涨幅序列

plt.scatter(today,yesterday)

plt.show()

2.外观调整

# 颜色，c。点大小，s,面积的意思。透明度，alpha。点形状，marker
plt.scatter(today,yesterday,s=100,c='r',marker='<',alpha=0.5,)
# 查看marker有多少种，去官网看下。
# 在同一个图中画多个。要用不同颜色和不同形状将其区分开

查看marker有多少种
https://matplotlib.org/api/markers_api.html?highlight=marker#module-matplotlib.markers

Pycharm功能强大，直接显示出备选参数

四.折线图

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates

x=np.linspace(-10,10,100) #np.linespace()函数，生成等距离的点
y=x**2
plt.plot(x,y) #.plot默认画出的就是折线图
plt.show()

# 用到日期数据作为x轴输入。日期数据要转化为matplotlib可识别的日期数据
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates

date,open,close=np.loadtxt('000001.csv',delimiter=',',converters={0:mdates.bytespdate2num('%m/%d/%Y')},skiprows=1,usecols=(0,1,4),unpack=True)
# mdates.bytespdate2num('%m/%d/%Y')，将'%m/%d/%Y'格式的字符串时间转化为matplotlib可识别的日期。不同文件中的日期格式不同，要针对不同格式写不同的格式化字符串。
plt.plot(date,open) #结果图，x轴是数字形式，不是日期形式。
# mdates.bytespdate2num('%m/%d/%Y')函数将date转换为matplotlib可识别的，实质上是将str形式转换为float形式。这里的date是float
# 要将float形式的date显示为时间形式.plot_date()函数专门绘制有一个轴是时间的。
# 程序可以自动识别为date，并将其转换为时间
plt.plot_date(date,open)  #结果不是折线图而是点图。plt.plot_date()默认是点图
# 添加参数，设定图的样式.
# 参数有线型linestyle，颜色color，点形状marker(标记),
plt.plot_date(date,open,'y-')
# 设定其他参数
plt.plot_date(date,open,linestyle='-',color='red',marker='o')
# 一次画两条线,就是两个画线函数同时写
plt.plot(date, open, color='red', linestyle='-', marker='o', markerfacecolor='yellow', markersize=12)
plt.plot(date, close, color='green', linestyle='--', marker='o',
markerfacecolor='blue', markersize=12)

plt.show()

这里关于mdates.strpdate2num(’%m/%d/%Y’)函数的使用要注意：

plt.plot(date,open) #结果图

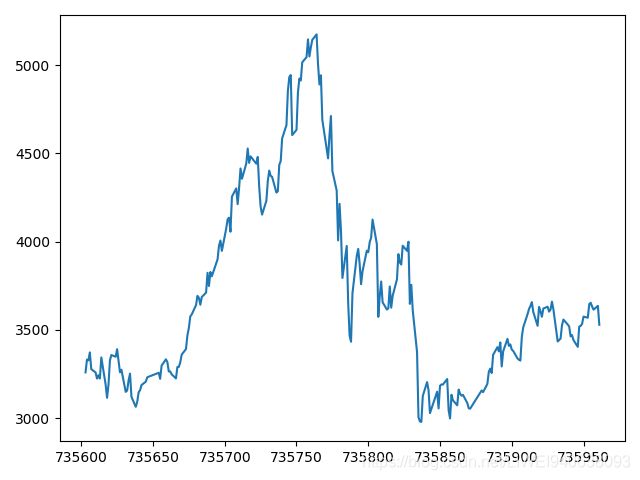
plt.plot_date(date,open) 结果图：

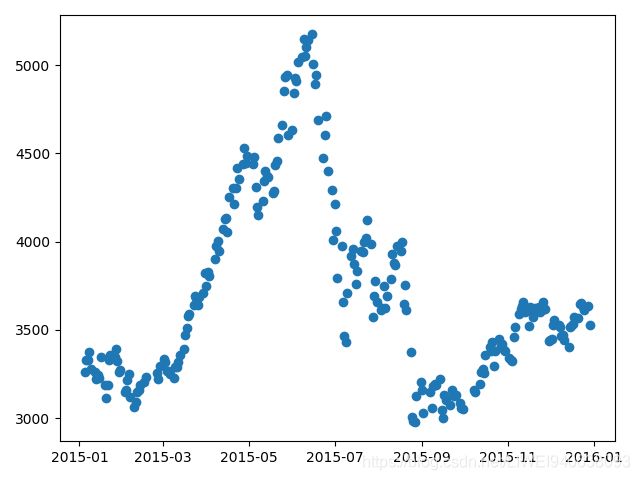
plt.plot_date(date,open,linestyle=’-’,color=‘red’,marker=‘o’)结果图

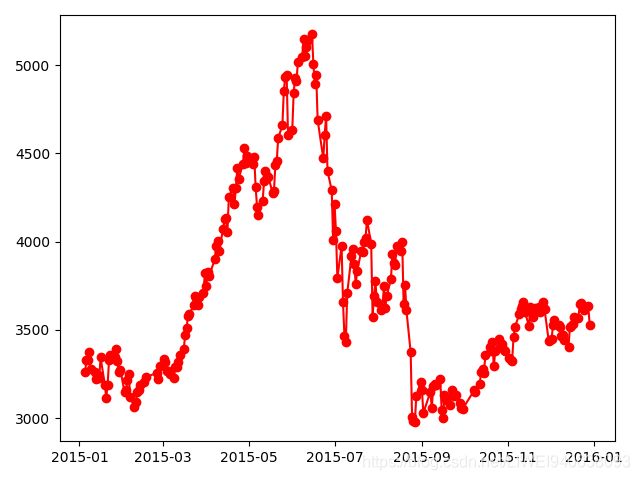
一次画两条线,就是两个画线函数同时写结果图

五.条形图

参考：https://www.cnblogs.com/zyg123/p/10504637.html

1.单条形图

import numpy as np
import matplotlib.pyplot as plt

N=5
y=[20,10,30,25,15]
index = np.arange(N)
p1 = plt.bar(x=index, height=y)
plt.show()

调整参数

p1 = plt.bar(x=index, height=y,width=0.5,bottom=100,color='red')
# width=0.5,柱状的宽度。
plt.show()

将纵向柱状图画为横向柱状图
需要把：orientation=“horizontal”，然后x,与y的数据交换，再添加bottom=x,即可。

p1 = plt.bar(x=index, height=y,width=0.5,bottom=100,color='red',orientation='horizontal')
# orientation='horizontal',orientation方向,柱状图的方向。
# 结果出错，问题出在：条形图的方向由纵向变为横向，x不再是图的横坐标，而是纵坐标，不将x作为index。

#改正。看起来很绕，但这正是灵活性的体现
p2 = plt.bar(x=0, bottom=index, width=y,color='red',height=0.5,orientation='horizontal')
plt.show()
#或者直接用barh()绘制
#plt.barh(y,width)绘制水平直方图，y:y轴上的位置，width:宽度，即每个直方图具体的数值
plt.barh(y=index,width=y)

出错的图

p2 = plt.bar(x=0, bottom=index, width=y,color=‘red’,height=0.5,orientation=‘horizontal’)结果

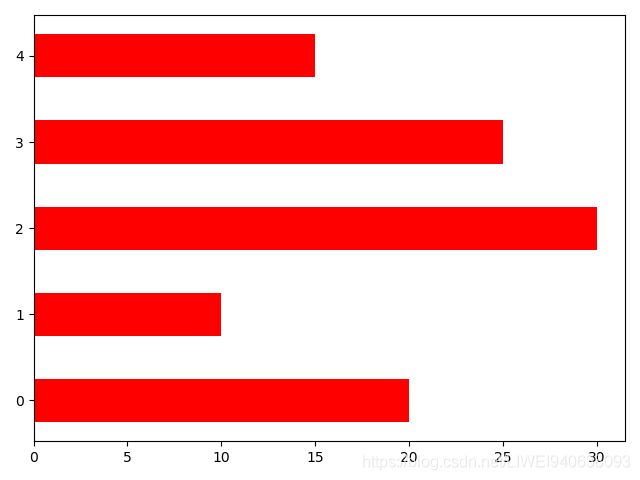
plt.barh(y=index,width=y)结果图：

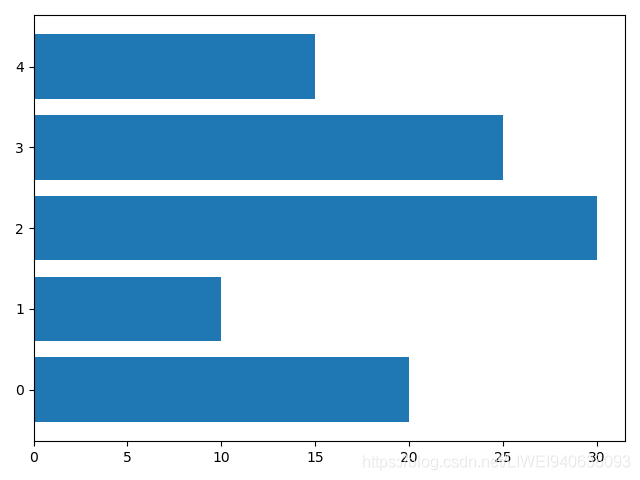
2.多条形图：层叠式和并列式

2.1纵向

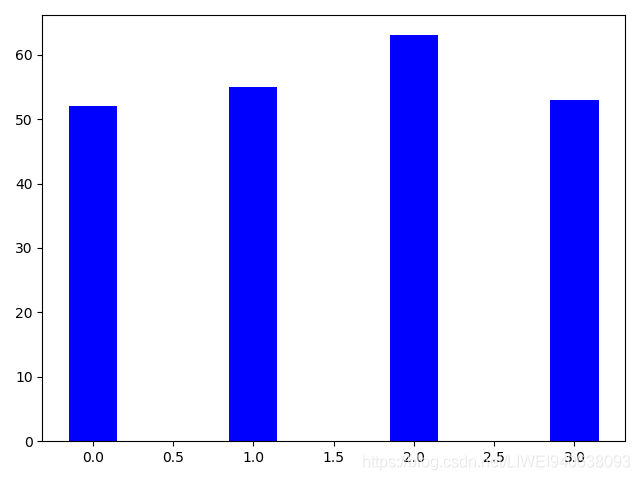
1. 并列式

import numpy as np
import matplotlib.pyplot as plt

index=np.arange(4)

sales_BJ=[52,55,63,53]
sales_SH=[44,66,55,41]

bar_width=0.3

plt.bar(index,sales_BJ,bar_width,color='b')
#上面，先画出一个条形图，bar(index,sales_BJ,bar_width,color='b')
plt.bar(index+bar_width,sales_SH,bar_width,color='r')
# 下面，再画一个bar。index+bar_width，x轴向右平移一个bar_width举例。
#要再加上bar，那就再往后加index+bar_width+bar_width

plt.bar(index,sales_BJ,bar_width,color=‘b’)

plt.bar(index,sales_BJ,bar_width,color=‘b’)
plt.bar(index+bar_width,sales_SH,bar_width,color=‘r’)

2. 层叠式

import numpy as np
import matplotlib.pyplot as plt

index=np.arange(4)

sales_BJ=[52,55,63,53]
sales_SH=[44,66,55,41]

#先画一个bar
plt.bar(index,sales_BJ,bar_width,color='b')
#下一个bar，高度直接从sales_BJ开始，即底部为bottom=sales_BJ。
plt.bar(index,sales_SH,bar_width,color='r',bottom=sales_BJ)
plt.show()

2.2横向图的层叠式和并列式

1. 并列式

import numpy as np
import matplotlib.pyplot as plt

index=np.arange(5)

sales_BJ=[52,55,63,53,40]
sales_SH=[44,66,55,41,30]

bar_width=0.3

plt.barh(y=index,width=sales_BJ,height=bar_width,color='b')
plt.barh(y=index+bar_width,width=sales_SH,height=bar_width,color='r')
plt.show()

2. ** 层叠式**

import numpy as np
import matplotlib.pyplot as plt

index=np.arange(5)

sales_BJ=[52,55,63,53,40]
sales_SH=[44,66,55,41,30]

bar_width=0.3

plt.barh(y=index,width=sales_BJ,height=bar_width,color='b')
plt.barh(y=index,width=sales_SH,left=sales_BJ,height=bar_width,color='r')
# 横向层叠图的关键是left=sales_BJ
plt.show()

六.直方图

• 由一系列高度不等的纵向条形组成，表示数据分布的情况
• 例如某年里同学的身高分布情况
• 注意和条形图的区别：直方图用来显示连续性的数值型数据，分组是连续性分组，并且可以自定义。条形图则是展示不同类别的数据，这些类别不能自定义且不连续。

举例说明：

import numpy as np
import matplotlib.pyplot as plt


mu = 100  # mean of distribution
sigma = 20  # standard deviation of distribution
x = mu + sigma * np.random.randn(2000)
# 随机生成2000个数据，均值为100，方差为20

plt.hist(x, bins=10,color='red',normed=True)
#bins=10，将连续数据分为10组等大小区间。normed=True，是否进行标准化。
#进行标准化后，每个区间对应的y轴不是出现的个数，而是出现的频率：即每个区间对应的个数除以总个数。

plt.hist(x, bins=50,color='green',normed=False)
# normed=False，没有进行标准化，每个区间对应的是个数。
# 只要样本数量足够大，分组数量足够多，这个直方图会越来越接近一条曲线。样本数量无穷大，分组数量无穷多时，直方图就是总体密度曲线。
plt.show()

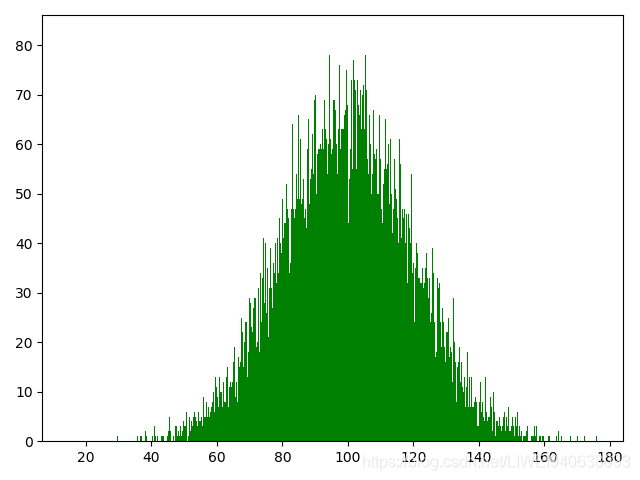
现在尝试增大样本数量，增加分组个数
只要样本数量足够大，分组数量足够多，这个直方图会越来越接近一条曲线。样本数量无穷大，分组数量无穷多时，直方图就是总体密度曲线。

import numpy as np
import matplotlib.pyplot as plt

mu = 100  # mean of distribution
sigma = 20  # standard deviation of distribution
x = mu + sigma * np.random.randn(20000)

plt.hist(x, bins=1000,color='green',density=False)
plt.show()

除了单变量直方图以外，还可以绘制双变量的联合的频率分布直方图。
在双变量的联合的频率分布直方图中，不是用y轴高度表示频率大小，而是用颜色深浅表示频率大小。
用来探索双变量的联合分布。

x = np.random.randn(1000)+2 #x的均值为2
y = np.random.randn(1000)+3 #y的均值为3

plt.hist2d(x, y, bins=40) #plt.hist2d()函数
plt.show()

x轴横坐标对应的中间点差不多是2，y轴纵坐标对应的中间点差不多是3.用颜色深浅表示频率大小。越往中间，频率越高，颜色越亮。

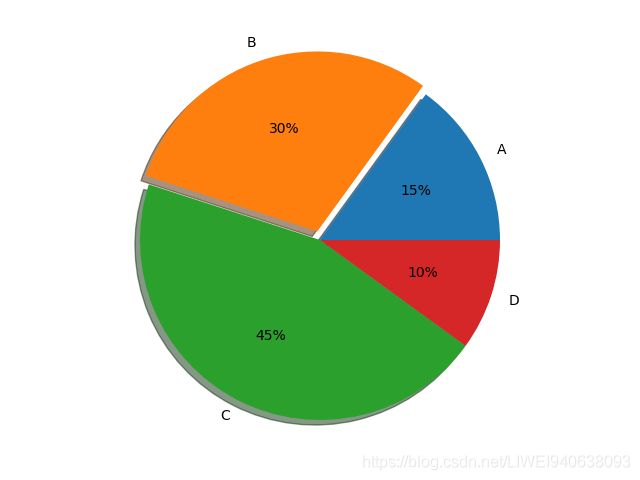
七.饼状图

• 饼状图显示一个数据系列中各项的大小与各项总和的比例
• 饼状图中的数据点显示为整个饼状图的百分比
• 如前十大品牌占市场份额图

import matplotlib.pyplot as plt

labels = 'A', 'B', 'C', 'D'
fracs = [15, 30, 45, 10]

plt.pie(x=fracs, labels=labels) #x=fracs，数据。labels，数据对应的标签。
plt.show()

加上其他参数

explode = (0, 0.05, 0, 0)

plt.pie(x=fracs, labels=labels,autopct='%.0f%%',explode=explode,shadow=True) #autopct,autopercent,将每一块所占的比例用python的格式化字符串或一个函数来表现出来，%.0f%%表示精确到百分数的整数位，%.1f%%表示精确到百分数后一位。explode,对应数据标签，每个数值代表举例圆中心的距离。shadow，阴影，增加立体感。
plt.show()

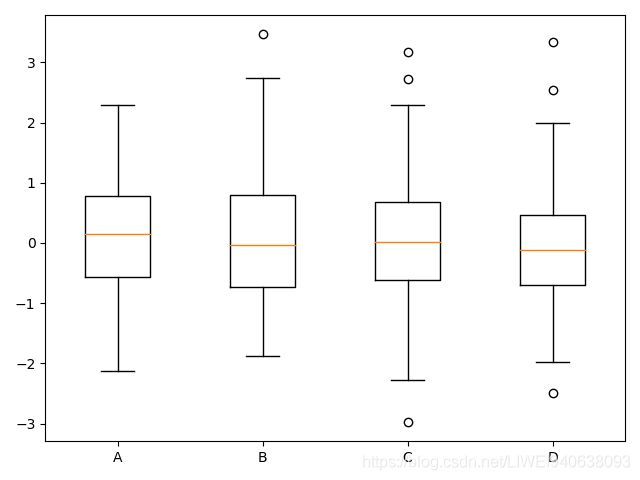
八.箱型图

• 箱型图(Box-plot)又称为盒须图、盒式图或箱线图。
• 是一种用作显示一组数据分散情况资料的统计图
• 上边缘，上四分位数，中位数，下四分位数，下边缘，异常值

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(100)

plt.boxplot(data,sym='o',whis=1.5)
# 参数：sym='o'，调整异常值数据点的形状。whis=1.5，代表边缘中间线的长度，比如希望将异常值纳入到边缘中，那就将whis调大，边缘中的线调长。whis默认是1.5，是比例值。
plt.show()

同时画几组数据
即在同一副图中显示几个箱型图

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(100)

data = np.random.normal(size=(100, 4), loc=0.0, scale=1.0)
# 生成4*1000的array。
labels = ['A','B','C','D']

plt.boxplot(data, labels=labels)

plt.show()

九.颜色和样式

1.颜色

1. 八种内建默认颜色缩写
   b:blue
   g:green
   r:red
   c:cyan 蓝绿色
   m:magenta 品红，洋红
   y:yellow
   k:black
   w:white
   其他颜色表示方法

• 灰色阴影
• html 十六进制
• RGB元组

举例说明

import numpy as np
import matplotlib.pyplot as plt

#默认情况
y=np.arange(1,5)
plt.plot(y)
plt.show()

调整颜色

import numpy as np
import matplotlib.pyplot as plt

# 为了区分开这些线，给了一些位移
y=np.arange(1,5)
plt.plot(y,'y');
# y为黄色
plt.plot(y+1,color=(0.1,0.2,0.3));
#颜色：RGB元组，
plt.plot(y+2,'#FF00FF');
#颜色：html 十六进制
plt.plot(y+3,color='0.5')
#颜色：灰色阴影，写上一个数字画出来的线就是一条灰色的线，数字代表颜色深度。
plt.show()

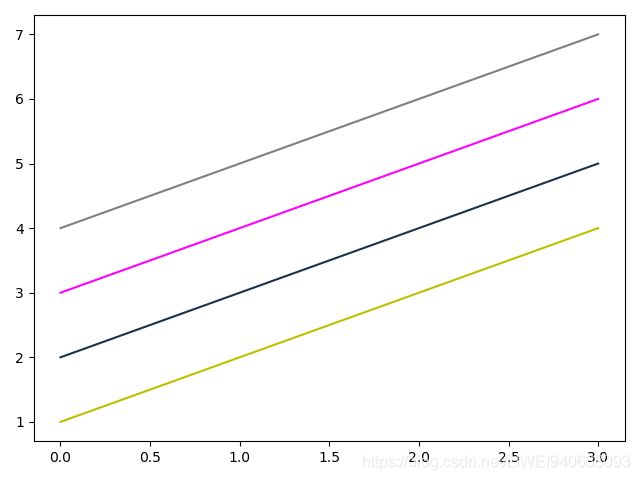
十六进制和RGB形式表示颜色，如何知道这个颜色的代码是多少
网上搜索，输入颜色代码，有许多查询颜色代码的工具

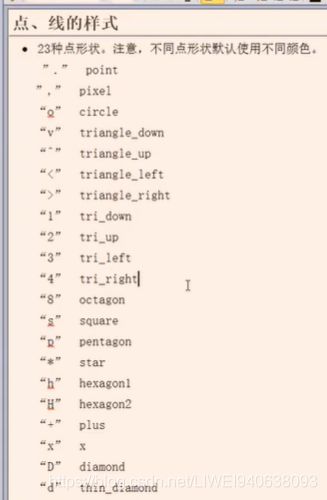
2.点、线的样式

举例说明：点样式

import numpy as np
import matplotlib.pyplot as plt

y=np.arange(1,5)

plt.plot(y,marker='o');
# 指定marker时会默认指定线段，不指定marker只画出一个点
plt.plot(y+1,'D');
plt.plot(y+2,'^');
plt.plot(y+3,'p');

plt.show()

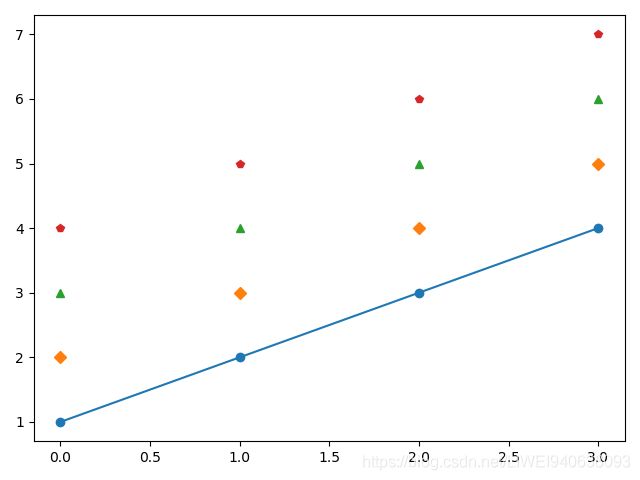
看图发现：除了第一条i线之外，其他线只有点没有线段，是因为第一个有marker，即指定marker时会默认指定线段。
没有指定颜色，但是仍然显示了不同颜色。matplotlib中使用不同点时，默认要在同一幅图中画不同数据，自动显示不同颜色。颜色排序按照8种内建默认颜色的顺序排序。

举例说明：线样式

import numpy as np
import matplotlib.pyplot as plt

y=np.arange(1,5)
plt.plot(y,'--');
plt.plot(y+1,'-.');
plt.plot(y+2,':');

plt.show()

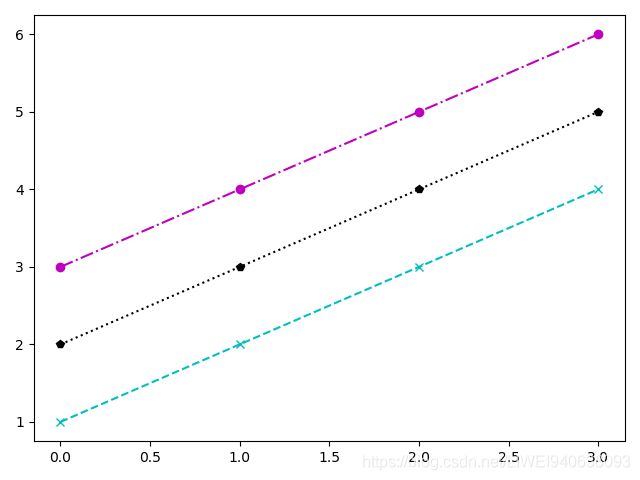
样式字符串
可以将颜色，点型，线型写成一个字符串,一个字符串可以同时表示颜色，点型，线型 。三个参数依次排列

• cx-- c是cyan 蓝绿色，x是点型，–是线性
• mo:
• ko-

import numpy as np
import matplotlib.pyplot as plt

y=np.arange(1,5)
plt.plot(y,'cx--');
plt.plot(y+1,'kp:');
plt.plot(y+2,'mo-.');

plt.show()

十.面向对象 VS Matlab Style

1.Matplotlib三种常用编程方式

1. pyplot，类似于Matlab的较简单方式。经典高层封装，
   简单易用，交互使用方便，可以根据命令实时作图，但底层定制能力不足。
2. • 封装更为彻底的pylab，将Matplotlib和Numpy合并的模块，模拟Matlab的编程环境。
3. 面向对象方式(Object-Oriented)方式，Matplot的精髓，更基础和底层的方式。
   综合使用pyplot和OO的方式，显示导入numpy。

总结，实战中综合使用pyplot和OO方式，显示导入numpy。
常用模块导入代码：
import matplotlib.pyplot as plt
import numpy as np

2.举例说明

1. pylab

#pylab
from pylab import * #是从pylab种导入所有函数，就是把numpy和pyplot中函数都导入进来。后面使用时就不用再加上前缀plt.plot()，np.arange(),而是直接使用。
x=arange(0,10,1)
y=randn(len(x))
plot(x,y)
title('random numbers')
show()

这种用法就跟matlab一样。

2. matplotlib.pyplot

#pyplot
import matplotlib.pyplot as plt
import numpy as np
x=np.arange(0,10,1)
y=np.random.randn(len(x))
plt.plot(x,y)
plt.title('pyplot')
plt.show()

把上面代码改成面向对象方式

#Object Oriented
import matplotlib.pyplot as plt
import numpy as np
x=np.arange(0,10,1)
y=np.random.randn(len(x))
# 先生成一个figure对象：画布对象或一张图对象
fig=plt.figure()
# 生成坐标轴对象，fig.add_subplot：在这个画布上画图，生成坐标轴对象
ax=fig.add_subplot(111)
# 画图
l,=plt.plot(x,y)
# 设定图标题
t=ax.set_title('object oriented')
plt.show()

对ax=fig.add_subplot(111)，l,=plt.plot(x,y)的说明：
https://www.jianshu.com/p/7b68e01952b4

十一.子图-subplot

利用面向对象，在同一幅图上画多个子图。可以用来对比

1.Matplotlib对象简介

• FigureCanvas画布
• Figure图
• Axes：在figure上生成坐标轴，即实际画图的地方

2.画子图实践

面向对象方式

1. fig=plt.figure()

• Figure实例
• 可以添加Axes实例

2. ax=fig.add_subplot(111)

• 返回Axes实例
• 参数1，子图总行数
• 参数2，子图总列数
• 参数3，子图位置
• 在Figure上添加Axes的常用方法

import matplotlib.pyplot as plt
import numpy as np

x=np.arange(1,100)

plt.subplot(221)
plt.plot(x,x)

plt.subplot(222)
plt.plot(x,-x)

plt.subplot(223)
plt.plot(x,x*x)

plt.subplot(224)
plt.plot(x,np.log(x))

plt.show()

pyplot中的函数

import matplotlib.pyplot as plt
import numpy as np

x=np.arange(1,100)
plt.subplot(221)
plt.plot(x,x)
plt.subplot(222)
plt.plot(x,x*x)

十二.多图–figure

子图–subplot是一张图上生成多个子图，多图–figure是直接生成多个图

import matplotlib.pyplot as plt

fig1=plt.figure()
ax1=fig1.add_subplot(111)
ax1.plot([1,2,3],[3,2,1])

fig2=plt.figure()
ax2=fig2.add_subplot(111)
ax2.plot([1,2,3],[1,2,3])

plt.show()

十三.网格

两种方式：plt的函数和面向对象

1. plt的函数

import numpy as np
import matplotlib.pyplot as plt
y=np.arange(1,5)

plt.plot(y,y*2)

plt.grid(True)

plt.show()
#交互中打开关闭网格
plt.grid()

对网格进行定制

import numpy as np
import matplotlib.pyplot as plt
y=np.arange(1,5)

plt.plot(y,y*2)

plt.grid(True,color='g',linestyle='-',linewidth='2')

plt.show()

2. 面向对象

#Object Oriented
import matplotlib.pyplot as plt
import numpy as np
x=np.arange(0,10,1)
y=np.random.randn(len(x))
fig=plt.figure()
ax=fig.add_subplot(111)
l,=plt.plot(x,y)

ax.grid(color='g')

plt.show()

注意：用面向对象的方式是没有交互效果的。在console中操作时，用plt方式每操作一步，都会有实时变化，而在面向对象过程中，操作一步不会有实时变化。因而，plt在console交互式模式下用的多，在脚本中使用面向对象。

十四.图例–legend

plt方式和面向对象方式

1. plt方式

import matplotlib.pyplot as plt
import numpy as np


x=np.arange(1,11,1)
y=x*x

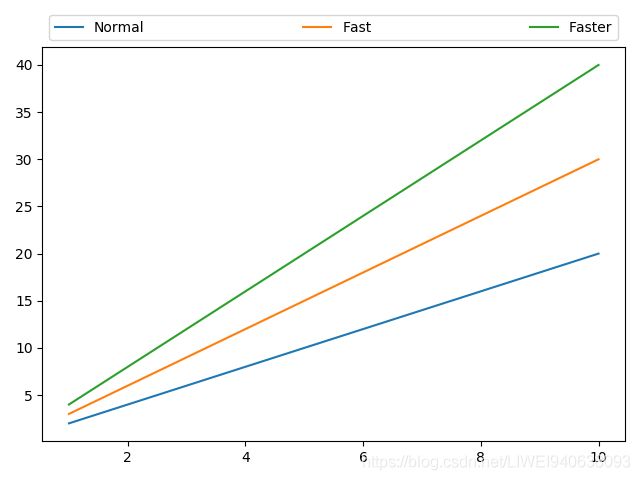
plt.plot(x,x*2,label='Normal') #名字用label代表

plt.plot(x,x*3,label='Fast')

plt.plot(x,x*4,label='Faster')
# 前面命名了，这里不写显示图例的话，还是不显示出来。
plt.legend(loc=0,ncol=3)
#图例参数：loc(loction),1，左上角，2，右上角，3，左下角，4，右下角。数字和loc的对应，官网可查到。
# ncol，图例按照几列显示。
plt.show()

loc和数字的对应：https://matplotlib.org/api/legend_api.html?highlight=legend#module-matplotlib.legend


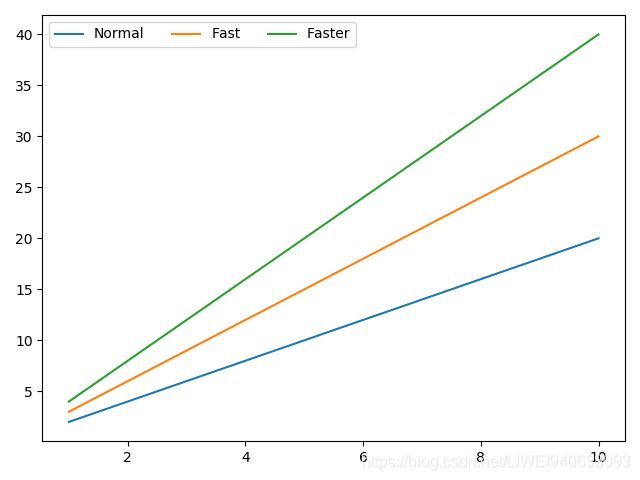
将label写到legend里面

plt.plot(x,x*2)
plt.plot(x,x*3)
plt.plot(x,x*4)

plt.legend(['Normal','Fast','Faster'])

plt.show()

2. 面向对象方式
   举例1

#OO
import matplotlib.pyplot as plt
import numpy as np
x=np.arange(0,10,1)
y=np.random.randn(len(x))
fig=plt.figure()
ax=fig.add_subplot(111)
l,=plt.plot(x,y) #画线
# 方法1：画legend
ax.legend(['ax legend'])
#方法2：画legend
line, =ax.plot(x,y,label='Inline label')
ax.legend()
#方法3：
line.set_label('label via method')
ax.legend()

plt.show()

举例2

import matplotlib.pyplot as plt
import numpy as np


x=np.arange(1,11,1)
y=x*x

plt.plot(x,x*2,label='Normal')

plt.plot(x,x*3,label='Fast')

plt.plot(x,x*4,label='Faster')

plt.legend(bbox_to_anchor=(0,1,1,0.1),loc=3,ncol=3,mode="expand")
# 
plt.show()

十五.坐标轴范围

方法1

import matplotlib.pyplot as plt
import numpy as np


x=np.arange(1,11,1)
y=x*x

plt.plot(x,x*2,label='Normal')

plt.plot(x,x*3,label='Fast')

plt.plot(x,x*4,label='Faster')

plt.legend(bbox_to_anchor=(0,1,1,0.1),loc=3,ncol=3,mode="expand")

plt.axis() #显示x、y轴坐标
plt.axis([-5,5,20,60]) #调整坐标范围，就是直接给坐标赋值，传递一个数组

plt.show()

方法2

import matplotlib.pyplot as plt
import numpy as np


x=np.arange(1,11,1)
y=x*x

plt.plot(x,x*2,label='Normal')

plt.plot(x,x*3,label='Fast')

plt.plot(x,x*4,label='Faster')

plt.legend(bbox_to_anchor=(0,1,1,0.1),loc=3,ncol=3,mode="expand")
# 方法2的子方法1
plt.xlim([-5,5]) #单个轴调整，可以只调整一个坐标轴
plt.ylim([0,60]) #
#方法2的子方法2
plt.xlim(xmin=-5,xmax=5) #
plt.xlim(xmin=-5) #只调整x轴的一边

plt.show()

十六.坐标轴刻度

将刻度调整得更密集或者更宽松

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(1,11,1)

plt.plot(x,x)

#获取当前图形的坐标轴，get current axis。
ax = plt.gca() 
# 调整坐标轴需要用到一个函数：ax.locator_params()
ax.locator_params(nbins=10,)
#nbins=10,刻度个数。
# 只调整x轴不调整y轴，进行指定
ax.locator_params('x',nbins=10)

对比面向对象方式

plt.locator_params('x',nbins=10)
ax.locator_params('y',nbins=10)

画时间序列的图，横坐标不是数字而是日期

# 面向对象方式
import matplotlib.pyplot as plt
import matplotlib as mpl 
import numpy as np
import datetime

fig=plt.figure()

start=datetime.datetime(2015.1.1) #日期的开始
stop=datetime.datetime(2016.1.1) #日期的结束
delta=datetime.timedelta(days=1) #日期的间隔
# mpl.dates.drange()函数生成matplotlib识别的dates序列。
dates=mpl.dates.drange(start,stop,delta)

y=np.random.rand(len(dates))
# 获取当前的坐标对象
ax=plt.gca()
#plot_date()绘制时间序列图形
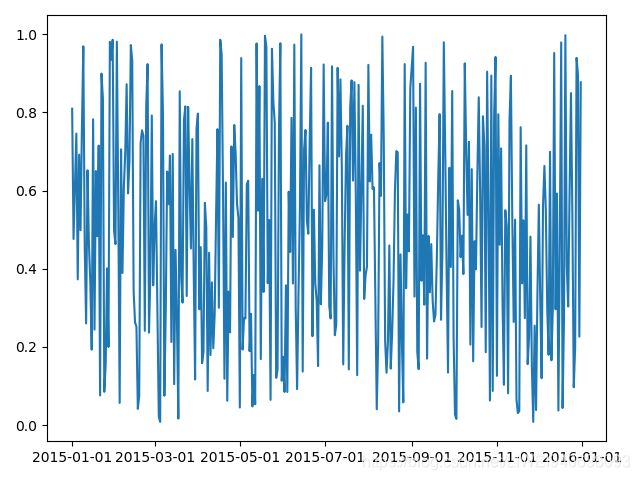
ax.plot_date(dates,y,linestyle='-',marker='')

plt.show()

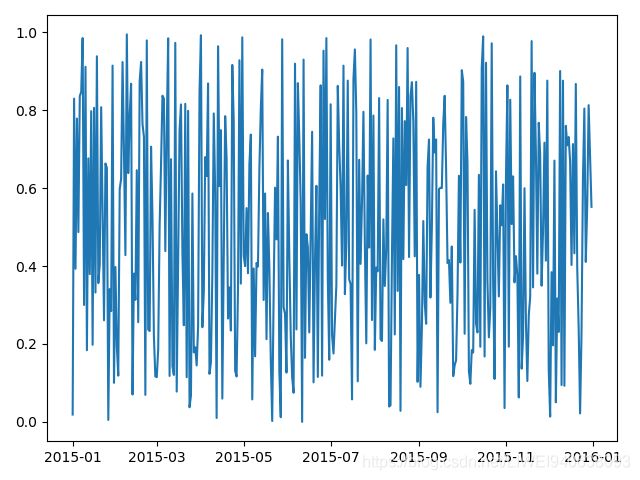
有几个问题需要考虑：1，x轴的日期在图像很小时会重合，
调整坐标轴刻度

y=np.random.rand(len(dates))
# 获取当前的坐标对象
ax=plt.gca()
#plot_date()绘制时间序列图形
ax.plot_date(dates,y,linestyle='-',marker='')
#调整坐标轴刻度的格式,如果要去掉天，就在()中去掉%d
date_format=mpl.dates.DateFormatter('%Y-%m-%d')
# 将调整好的date_format应用到坐标轴上
ax.xaxis.set_major_formatter(date_format)
#避免刻度重叠
fig.autofmt_xdate() #坐标刻度根据图形大小自适应，自适应会调整大小和角度
plt.show()

画图时将坐标轴刻度设置成向内方向，设置背景网格线为虚线
https://blog.csdn.net/qq_41821678/article/details/105803150

十七.添加坐标轴

在一个平面图中画两条线，不同的线对应的刻度不同，双坐标轴
pyplot方式

import matplotlib.pyplot as plt

import numpy as np

x=np.arange(2,20,1)
y1=x*x
y2=np.log(x)

plt.plot(x,y1)

#添加一条坐标轴
plt.twinx() #添加坐标轴，刻度默认是从0到1
plt.plot(x,y2,'r')

plt.show()

面向对象方式

import matplotlib.pyplot as plt
import numpy as np

x=np.arange(2,20,1)
y1=x*x
y2=np.log(x)

fig=plt.figure()
ax1=fig.add_subplot(111)
ax1.plot(x,y)
ax1.set_ylabel('Y1')
ax1.set_xlabel('Compare Y1 and Y2')

ax2=ax1.twinx()
ax2.plot(x,y2,'r')
ax2.set_ylabel('Y2')

plt.show()

将x轴设定为两个双x轴

import matplotlib.pyplot as plt
import numpy as np

x=np.arange(2,20,1)
y1=x*x
y2=np.log(x)
plt.plot(y1,x)

plt.twiny()
plt.plot(y2,x.color='r')

plt.show()

十八.注释

在图形上强调某个地方，给别人信息提示
annotate，注释；给…作注释或评注

import matplotlib.pyplot as plt
import numpy as np

x=np.arange(-10,11,1)
y=x*x

plt.plot(x,y)

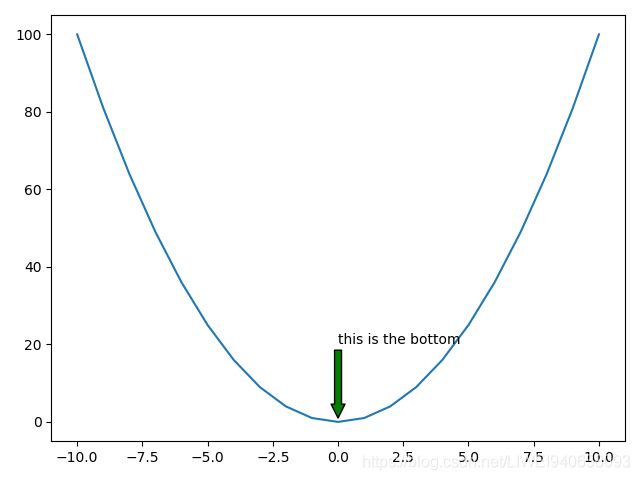
plt.annotate('this is the bottom',xy=(0,1),xytext=(0,20),arrowprops=dict(facecolor='g',headlength=10,headwidth=10,width=5))
# 'this is the bottom'，箭头名。xy=(0,1),箭头头部位置，xytext=(0,20)，箭头尾部位置，也是箭头名位置。arrowprops，调整箭头自身的属性。
#arrowprops=dict(facecolor='g',headlength=10,headwidth=10,width=5))，facecolor箭头颜色；headlength，箭头头部长度；headwidth=10箭头宽度；width=5箭头宽度。
plt.show()

十九.文字

在图中只有纯文字标注，不再有箭头。

import matplotlib.pyplot as plt
import numpy as np

x=np.arange(-10,11,1)
y=x*x

plt.plot(x,y)

# 只有纯文字标注，plt.text()函数
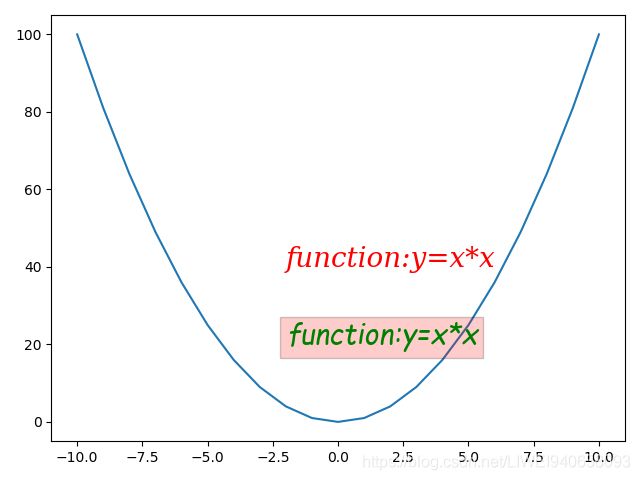
plt.text(-2,40,'function:y=x*x',family='serif',size=20,color='r',style='italic'，weight=100)
#0,40是位置。
#文字标注的属性参数
plt.text(-2,20,'function:y=x*x',family='fantasy',size=20,color='g',style='obliqu'，weight='light',bbox=dict(facecolor='r',alpha=0.2))
#family,字体，官方网站可查到字体种类。size,字体大小。style,字体是否倾斜。weight,字体加粗，用数字或者文字。bbox,文字外面加方框,bbox=dict(facecolor='r',alpha=0.2)颜色，透明度。

plt.show()

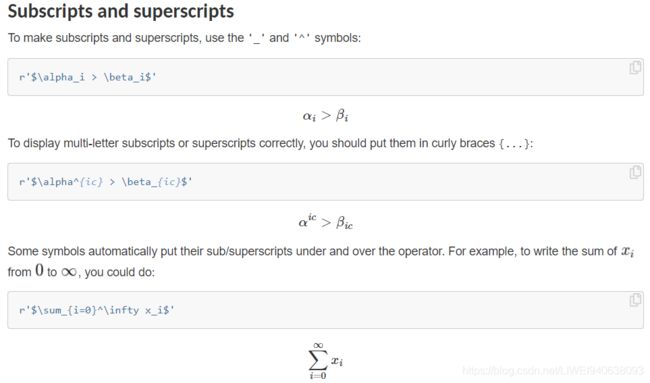
二十.特殊文字：Tex公式

参考：https://matplotlib.org/tutorials/text/mathtext.html

在word中编辑数学公式，不容易，因为有很多奇怪的符号。Matplotlib很好地解决了这个问题，因为用了Tex公式。

• matplotlib自带mathtext引擎，不需要安装TeX系统
  TeX系统是一个在学术界用途广泛地用来做文本编辑的排版系统
• ￥作为开始和结束符，如”$ y=x+z $"。绘制图形时会自动识别出来字符串，并且将其解析为所需要的对应公式。
  公式系统复杂，其中的符号有很多种，matplotlib官网上有对数学公式的专门介绍文档。

Tex公式Symbol说明

Tex公式下标说明

举例说明

import matplotlib.pyplot as plt

fig=plt.figure()

ax=fig.add_subplot(111)

ax.set_xlim([1,7])
ax.set_ylim([1,5])

# 面向对象方式
ax.text(2,4,r"$ \alpha_i \beta_j \pi \lambda \omega $",size=25)
# 位置是2,4。然后是python的字符串，r""代表字符串不转译，将所有字符视为字符本身，主要是针对反斜杠转义字符。
# 在官网上查看数学公式所代表的符号。
ax.text(4,4,r"$ sin(0)=cos(\frac{\pi}{2})$",size=25)
ax.text(2,2,r"$ \lim_{x \rightarrow y} \frac{1}{x^3}$",size=25)
# lim_,这个下划线会自动识别是在右下角还是在正下方。
ax.text(4,2,r"$ \sqrt[4]{x} = \sqrt[2]{y}$",size=25)

plt.show()

二十一.工具栏

二十二.区域填充

给一块白块区域上色

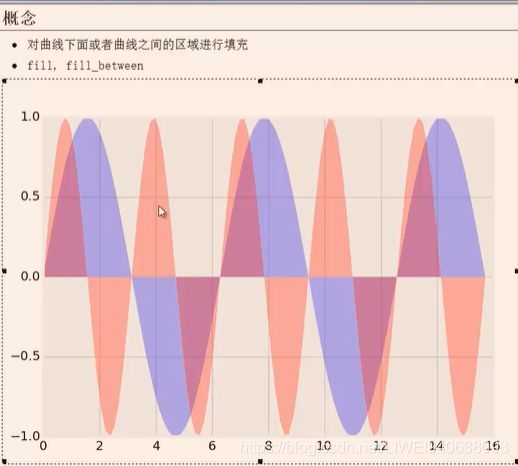
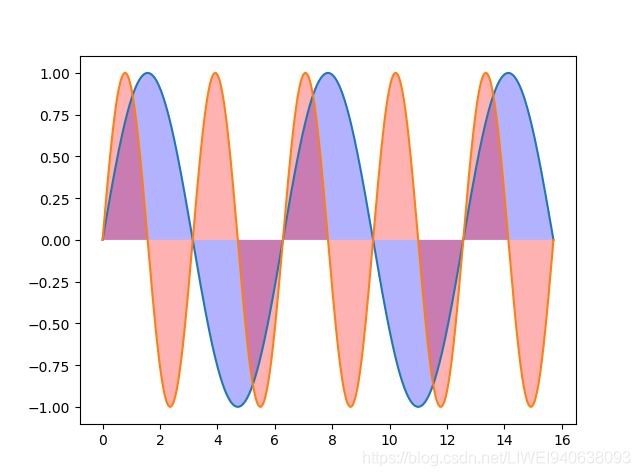
plt.fill()填充的是曲线和x轴之间的区域

import matplotlib.pyplot as plt
import numpy as np

x=np.linspace(0,5*np.pi,1000)

y1=np.sin(x)
y2=np.sin(2*x)

plt.plot(x,y1)
plt.plot(x,y2)

# 填充颜色，plt.fill()填充的是曲线和x轴之间的区域
plt.fill(x,y1,'b',alpha=0.3)
plt.fill(x,y2,'r',alpha=0.3)
# 为了将上面两个都显示出来，更改透明度

plt.show()

fill_between填充两条曲线之间的区域

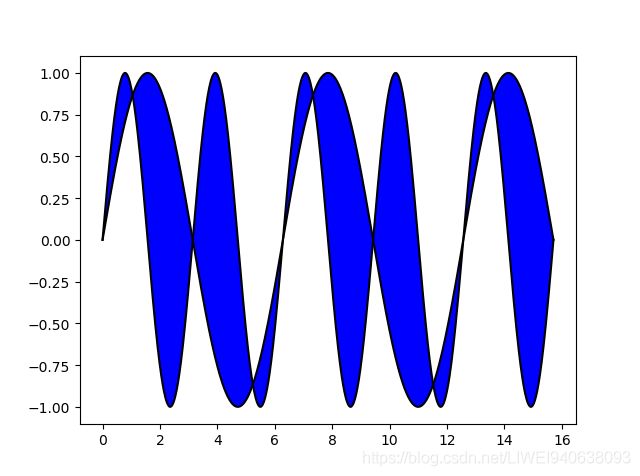
1. 填充为一样的颜色

import matplotlib.pyplot as plt
import numpy as np

x=np.linspace(0,5*np.pi,1000)
y1=np.sin(x)
y2=np.sin(2*x)

fig=plt.figure()
ax=plt.gca() #得到现在的坐标轴
ax.plot(x,y1,x,y2,color='black')
#fill_between
ax.fill_between(x,y1,y2,facecolor='blue')

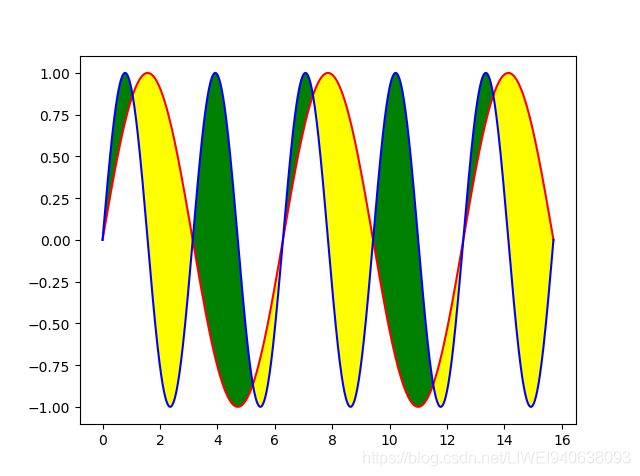
2. 填充为不同颜色

import matplotlib.pyplot as plt
import numpy as np

x=np.linspace(0,5*np.pi,1000)
y1=np.sin(x)
y2=np.sin(2*x)

fig=plt.figure()
ax=plt.gca() #得到现在的坐标轴
ax.plot(x,y1,color='r')
ax.plot(x,y2,color='b')
# 在哪里填充，加上参数where;interpolate=True参数将两条曲线之间的离散点上空白部分填充
ax.fill_between(x,y1,y2,where=y1>y2,facecolor='yellow',interpolate=True)
ax.fill_between(x,y1,y2,where=y2>y1,facecolor='green',interpolate=True)

plt.show()

二十三.填充形状:生成图形

生成图形的matplotlib.patches官方文档，https://matplotlib.org/api/patches_api.html?highlight=patch#module-matplotlib.patches

如何直接在图形上画一个填充好的形状

生成一个圆形

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.patches as mpatches

#生成一个图
fig, ax=plt.subplots()

# 给定图的坐标，即图的位置.图的中心坐标
xy1=np.array([0.2,0.2])
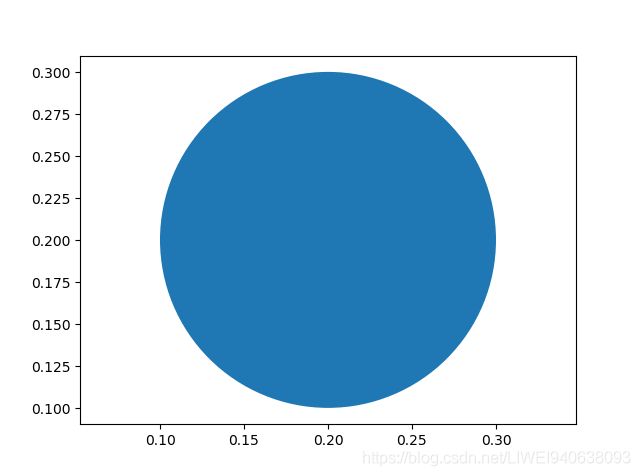
# mpatches.Circle()函数，参数：xy1是位置，0.1是半径
circle=mpatches.Circle(xy1,0.1)
# 生成了这个图对象，要把这个图放到画布上去
ax.add_patch(circle)
# 结果生成的图不是一个正圆形。是因为x轴和y轴的坐标比例不正确。
# 调整x轴和y轴比例
plt.axis('equal')
# 添加网格
plt.grid()

plt.show()

生成多个图形

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.patches as mpatches

#生成一个图
fig, ax=plt.subplots()

# 给定图的坐标，即图的位置.
xy1=np.array([0.2,0.2])
xy2=np.array([0.2,0.8])
xy3=np.array([0.8,0.2])
xy4=np.array([0.8,0.8])

#画圆形
# mpatches.Circle()函数，参数：xy1是位置，0.1是半径
circle=mpatches.Circle(xy1,0.1)
# 生成了这个图对象，要把这个图放到画布上去
ax.add_patch(circle)
# 结果生成的图不是一个正圆形。是因为x轴和y轴的坐标比例不正确。
# 调整x轴和y轴比例

#画长方形
rect=mpatches.Rectangle(xy2,0.2,0.1,color='r') 
#方形的坐标代表的不是中心的位置，而是左下角点的位置
ax.add_patch(rect)

#画多边形,mpatches.RegularPolygon()函数，参数：位置，几条边，半径长度(即圆心到每个顶点的长度）。
# 多边形的边特别多，无穷多时，就类似于一个圆
polygon=mpatches.RegularPolygon(xy3,5，0.1，color='g')
ax.add_patch(polygon)

#画椭圆.参数：位置即圆心.长直径和短直径。
ellipse=mpatches.Ellipse(xy4,0.4,0.2,color='y')
ax.add_patch(ellipse)

plt.axis('equal')
# 添加网格
plt.grid()

plt.show()

二十四.样式–美化

举例说明

import numpy as np
import matplotlib.pyplot as plt

plt.style.use('ggplot')

fig, axes=plt.subplots(ncols=2,nrows=2) #生成2行2列的4个子图

ax1, ax2, ax3, ax4 = axes.ravel()

#画第一个图
x, y=np.random.normal(size=(2,100))
ax1.plot(x,y,'o')

#画第二个图
x=np.arange(0,10)
y=np.arange(0,10)

ncolors=len([u'b',u'g',u'r',u'c',u'm',u'y',u'k']) #plt.rcParams['axes.color_cycle']表示产生
# 颜色的循环[u'b',u'g',u'r',u'c',u'm',u'y',u'k']对七种颜色依次画出线

shift=np.linspace(0,10,ncolors)

for s in shift:
    ax2.plot(x,y+s,'-')

#画第三幅图
x=np.arange(5)
y1,y2,y3=np.random.randint(1,25,size=(3,5))
width=0.25

ax3.bar(x,y1,width)
ax3.bar(x+width,y2,width,color=[u'b',u'g',u'r',u'c',u'm',u'y',u'k'][1])
ax3.bar(x+2*width,y2,width,color=[u'b',u'g',u'r',u'c',u'm',u'y',u'k'][2])

#画第四个图
for i, color in enumerate([u'b',u'g',u'r',u'c',u'm',u'y',u'k']):
    xy=np.random.normal(size=2)#随机的坐标轴
    ax4.add_patch(plt.Circle(xy,radius=0.3,color=color))

ax4.axis('equal') #把x，y轴调整对称

plt.show()

matplotlib.rcParams参考：https://blog.csdn.net/helunqu2017/article/details/78652261，https://blog.csdn.net/weixin_34378922/article/details/94027767，https://blog.csdn.net/qq_27825451/article/details/81630839。

二十五.极坐标

极坐标有两个维度，1，角度，2，半径。角度和半径形成的坐标体系叫做极坐标。

点1，角度是0，半径是1，点2，角度是90度，半径是2.
举例1

import numpy as np
import matplotlib.pyplot as plt

#生成1到5的半径
r=np.arange(1,6,1)
# 生成角度
theta=[0,np.pi/2,np.pi,3*np.pi/2,2*np.pi]

#生成一个图
ax=plt.subplot(111,projection='polar')
# projection='polar',投影未极坐标。
ax.plot(theta,r,color='r',linewidth=3)
ax.grid(True)

plt.show()

举例2

import numpy as np
import matplotlib.pyplot as plt

# 生成元素为5的数组array
#r=np.empty(5):array([0. , 0.25, 0.5 , 0.75, 1.])
r=np.empty(5)
r.fill(5)
# 角度
theta=[0,np.pi/2,np.pi,3*np.pi/2,2*np.pi]

ax=plt.subplot(111,projection='polar')
ax.plot(theta,r,color='r',linewidth=3)
ax.grid(True)

plt.show()

举例3
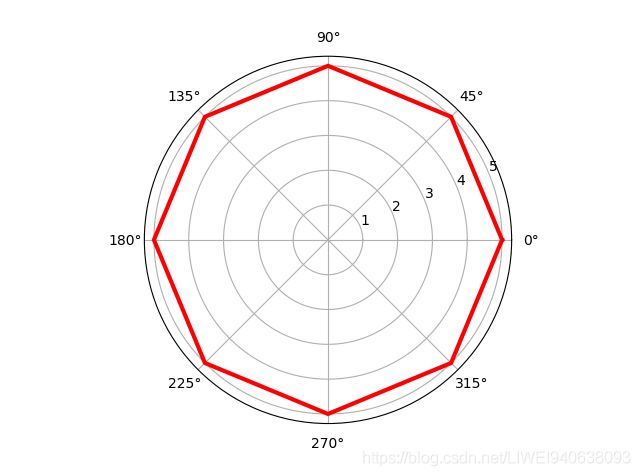
生成8边形，角度要分得更细，共有9个数据点(有一个地方两点重合)，

import numpy as np
import matplotlib.pyplot as plt

# 生成9个数据点，那就是个数为9个的array
#r=np.empty(5):array([0. , 0.25, 0.5 , 0.75, 1.])
r=np.empty(9)
r.fill(5)
# 角度
#360度，即2pi平均分成8份，  
pi_two=np.pi*2
theta=[0,pi_two/8,2*pi_two/8,3*pi_two/8,4*pi_two/8,
       5*pi_two/8,6*pi_two/8,7*pi_two/8,8pi_two/8]

ax=plt.subplot(111,projection='polar')
ax.plot(theta,r,color='r',linewidth=3)
ax.grid(True)

plt.show()

二十六.实践–函数积分图

过程是：边查文档边画图

分析如何画图：先画出那条线，之后在里面写好函数
过程
1，图中坐标轴不显示刻度：
如何画，搜一下坐标轴对象，axes有哪些相关方法：
参考网址：参考网址：https://matplotlib.org/api/pyplot_api

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon

def func(x):
 return -(x-2)*(x-8)+40

x=np.linspace(0,10)

y=func(x)

fig, ax=plt.subplots()

plt.plot(x,y,'r',linewidth=2)
a=2
b=9

ax.set_xticks([a,b])

ax.set_yticks([])

ax.set_xticklabels(['$a$','$b$'])

ix=np.linspace(a,b)
iy=func(ix)

ixy=zip(ix,iy)

verts=[(a,0)]+list(ixy)+[(b,0)] #产生规则的数组

poly=Polygon(verts,facecolor='0.9',edgecolor='0.5') #生成poly对象，数字越大，颜色越浅

ax.add_patch(poly)

plt.figtext(0.9,0.05,'$x$')#x轴标记
plt.figtext(0.1,0.9,'$y$')

#添加函数的数学公式
x_math=(a+b)*0.5
y_math=35

plt.text(x_math,y_math,r'$\int_a^b (-(x-2)*(x-8)+40)dx$',horizontalalignment='center')#按照中间对齐
plt.ylim(ymin=25)#将位置y坐标调小一点
plt.show()

二十七.实践:散点–条形图

import numpy as np
import matplotlib.pyplot as plt


plt.style.use('ggplot')#决定风格

x=np.random.randn(200)#随机生成200个随机数
y=x+np.random.randn(200)*0.5

#定义变量
margin_border=0.05
width=0.4
margin_between=0.05
height=0.2

#生成三个图的坐标轴
#主图
left_s=margin_border
bottom_s=margin_border
height_s=width
width_s=width

left_x=margin_border
bottom_x=margin_border+width+margin_between
height_x=height
width_x=width

left_y=margin_border+width+margin_between
bottom_y=margin_border
height_y=width
width_y=height

plt.figure(1,figsize=(8,8)) #生成一个8*8的画布

rect_s=[left_s,bottom_s,width_s,height_s]
rect_x=[left_x,bottom_x,width_x,height_x]
rect_y=[left_y,bottom_y,width_y,height_y]

axScatter=plt.axes(rect_s)
axHisX=plt.axes(rect_x)
axHisY=plt.axes(rect_y)

#去掉图一的x轴标注和图三的y轴标注
axHisX.set_xticks([])
axHisY.set_yticks([])

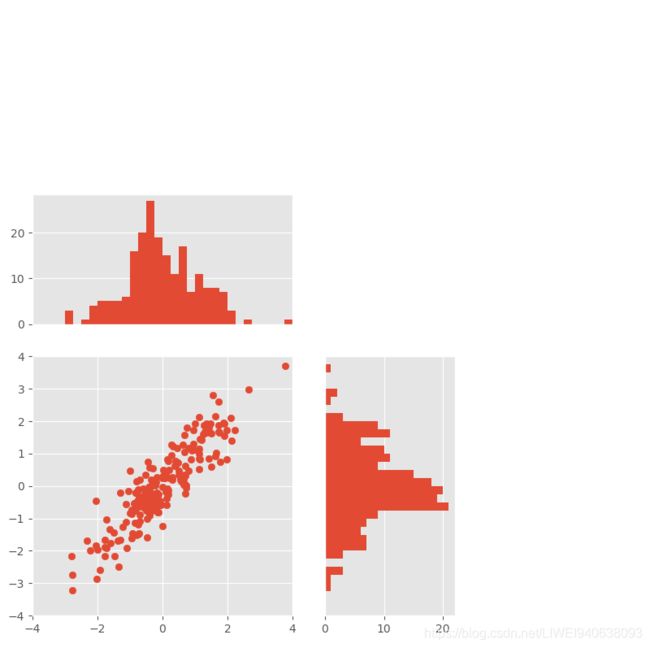
#画散点图
axScatter.scatter(x,y)

bin_width=0.25

xymax=np.max([np.max(np.fabs(x)),np.max(np.fabs(y))])

lim=int(xymax/bin_width+1)*bin_width#得到图形精确宽度值

axScatter.set_xlim(-lim,lim)#对图形的x轴和y轴进行限制
axScatter.set_ylim(-lim,lim)

#画条形图
bins=np.arange(-lim,lim+bin_width,bin_width)#以bin_width为步长

axHisX.hist(x,bins=bins)
axHisY.hist(y,bins=bins,orientation='horizontal')
#设置柱形图的坐标范围
axHisX.set_xlim(axScatter.get_xlim())
axHisY.set_ylim(axScatter.get_ylim() )

plt.show()

二十八.实践:球员能力图

#_*_ coding:utf-8 _*_
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import  FontProperties #显示的定义所要使用的字体 _

plt.style.use('ggplot')

font=FontProperties(fname=r'c:\windows\fonts\simsun.ttc',size=12)

ability_size=6
ability_label=['进攻','防守','盘带','速度','体力','射术']

ax1=plt.subplot(221,projection='polar') #生成2行2列的第一个极坐标子图
ax2=plt.subplot(222,projection='polar')
ax3=plt.subplot(223,projection='polar')
ax4=plt.subplot(224,projection='polar')

#随机生成学员的能力值
player={
    'M':np.random.randint(size=ability_size,low=60,high=99),
    'H':np.random.randint(size=ability_size,low=60,high=99),
    'P':np.random.randint(size=ability_size,low=60,high=99),
    'Q':np.random.randint(size=ability_size,low=60,high=99),
}

theta=np.linspace(0,2*np.pi,6,endpoint=False)#生成极坐标的角度

theta=np.append(theta,theta[0])#使首尾拼接

player['M']=np.append(player['M'],player['M'][0]) #使M产生的数值形成首尾相接闭环的效果
ax1.plot(theta,player['M'],'r')#绘制首尾相接的图
ax1.fill(theta,player['M'],'r',alpha=0.3) #用红色填充
ax1.set_xticks(theta)#定义成6等分的ticks
ax1.set_xticklabels(ability_label,y=0.1,fontproperties=font)
ax1.set_title(u'梅西',fontproperties=font,color='r',size=20)

player['H']=np.append(player['H'],player['H'][0]) #使M产生的数值形成首尾相接闭环的效果
ax2.plot(theta,player['H'],'g')#绘制首尾相接的图
ax2.fill(theta,player['H'],'g',alpha=0.3) #用红色填充
ax2.set_xticks(theta)#定义成6等分的ticks
ax2.set_xticklabels(ability_label,y=0.1,fontproperties=font)
ax2.set_title(u'哈维',fontproperties=font,color='g',size=20)

player['P']=np.append(player['P'],player['P'][0]) #使M产生的数值形成首尾相接闭环的效果
ax3.plot(theta,player['P'],'b')#绘制首尾相接的图
ax3.fill(theta,player['P'],'b',alpha=0.3) #用红色填充
ax3.set_xticks(theta)#定义成6等分的ticks
ax3.set_xticklabels(ability_label,y=0.1,fontproperties=font)
ax3.set_title(u'皮克',fontproperties=font,color='b',size=20)

player['Q']=np.append(player['Q'],player['Q'][0]) #使M产生的数值形成首尾相接闭环的效果
ax4.plot(theta,player['Q'],'y')#绘制首尾相接的图
ax4.fill(theta,player['Q'],'y',alpha=0.3) #用红色填充
ax4.set_xticks(theta)#定义成6等分的ticks
ax4.set_xticklabels(ability_label,y=0.1,fontproperties=font)
ax4.set_title(u'切赫',fontproperties=font,color='y',size=20)


plt.show()

二十九.实践:股票K线图

参考：https://blog.csdn.net/qq_41511262/article/details/102966270