深度学习笔记 - FCN模型与上采样（Upsampling）

目录

1. FCN模型

2. 上采样

2.1 双线性插值上采样（今天不做重点介绍）

2.2 反卷积上采样

（1）数学理解

（2）动态过程理解

2.3 反池化上采样

---

引言：在FCN、U-net等网络结构中，涉及到了上采样。上采样概念：上采样指的是任何可以让图像变成更高分辨率的技术。

发现了几个较好的教程帮助理解FCN和上采样：

（1）教程1：FCN详解与pytorch简单实现；反卷积的数学理解

（2）教程2：3种上采样方法（反卷积，上池化，线性插值）

1. FCN模型

CNN与FCN模型

                                                                                                                                                                                                    

FCN模型具体过程

                                                                                                                                                                                               

（1）FCN发布于2014年，基于CNN卷积模型，是语义分割领域全卷积网络的开山之作；

（2）FCN以端到端的方式训练，执行像素到像素的语义分割；

（3）主要思路：FCN用卷积和上采样层替换传统CNN中的完全连接层来执行语义分割任务；

（4）最核心的思想是特征图的融合：假设最后的输出为pool5产生的x，利用转置卷积上采样，放大32倍，得到FCN-32s；将x上采样放大2倍，和pool4产生的特征图直接相加，再上采样放大16倍，得到FCN-16s；将FCN-16s进行上采样放大2倍，与pool3产生的特征图直接相加，在放大8倍，得到FCN-8s。这也是FCN最有特色和有趣的地方。

2. 上采样

概念：上采样指的是任何可以让图像变成更高分辨率的技术。可以理解为把经过不断卷积和池化后宽和高都缩小的image恢复到特定尺寸的过程。

上采样一般有以下3种方法：

2.1 双线性插值上采样（今天不做重点介绍）

2.2 反卷积上采样

 反卷积上采样是对卷积的逆过程，可以通过以下2种方式进行理解：

（1）数学理解

首先要理解卷积过程的数学表述，如：input为4*4的图像，表示为：

卷积核kernel的尺寸为3 x 3，表示为：

步长 strides = 1，填充 padding = 0 ，即 i = 4, k=3, s=1, p=0。则按照卷积计算公式 Output = (i+2p-k) \ s + 1，输出图像 的尺寸为 2 x 2。

用线性代数中的矩阵乘法来描述卷积过程，首先将其展开为一维向量：

注意：为什么要展开为一维？

我的理解是：input为4*4，output为2*2,根据线性代数内的矩阵乘法运算，该过程是无法完成的。所以只有把input变为16*1，输出为4*1，才有可能完成矩阵运算过程。

因此：

input = X = [x1, x2, …, x16]T
output = Y = [y1, y2, y3, y4]T

卷积过程可表述为：

Y= CX

让我们看一下卷积核C以什么矩阵形式来完成卷积过程的（C的推导留个坑以后补充）：

重点来了：如果我们要求反卷积，把图像由小变大，即求X, 则：

反卷积的尺寸计算公式如下，推导过程可看这篇文章：

o:output    s:stride   i:input   p:padding   k:Kernal

至此，我们知道了反卷积如何计算，以及反卷积的尺寸计算公式。

（2）动态过程理解

CSDN上有很多动态过程介绍，可以直观显示其过程。但个人认为，要想深入理解反卷积过程到底做了什么，理解其数学过程是最根本的做法。

当然，对于初学者而言（包括我），动态过程能够帮我们降低理解难度，我在这里也贴上一篇介绍：

•  反卷积过程

2.3 反池化上采样

反池化过程主要介绍两种池化：

• 反最大池化：反池化时要记录最大值所在的位置，然后其余位置用0补充。
• 反平均池化：一般用邻近元素作填充。

图像理解：

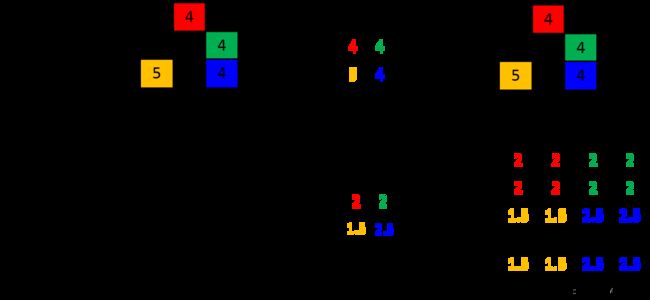2种反池化