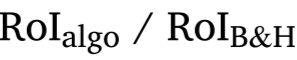解读:机器学习预测收益模型应该采取哪种度量指标
写在前面
下面这篇文章的内容主要是来自发表于Expert Systems with Applications 的一篇文章《Machine learning models predicting returns: Why most popular performance metrics are misleading and proposal for an efficient metric》。这篇文章就目前人工智能模型在预测股票收益采用的常见评估指标提出了一些思考,并提出了一种新的评估指标。除此之外,这篇文章还对最近190篇已发表的相关论文进行统计,分析并讨论了它们用到的评估指标。原论文以及源码在文末进行获取。
1
摘要
如今已有许多机器学习模型已经被开发出来,以实现优化投资策略的风险回报为目标。在这篇文章中,(a)介绍并分类了190篇相关文章中使用的最流行的度量指标。这篇文章注意到,在大多数现有的文章中,并没有用于比较不同算法之间差异的标准。(b)探究了不同文献中用于提高投资结果指标的能力,并且证明了许多最流行的度量标准,如均方误差(MSE)、均方根误差(RMSE)、准确率以及F1,不适合用于此目的。除此之外,解释了为什么基于风险调整的回报率指标是同类中最好的,尽管它们存在统计上的局限性,不允许对不同资产或不同时间的算法进行简单的比较。(c)提出了一种新的度量指标,用于衡量人工智能模型风险收益,该指标在统计上更加稳健,可以测试模型在不同时间和资产中的有效性和稳定性。
2
常见的度量指标
这篇文章回顾了190篇文章的内容,包括用于预测未来资产回报的ML或DL算法,或基于RL算法的投资策略。发现用到的度量指标非常多样化,主要包括下面几种类别:
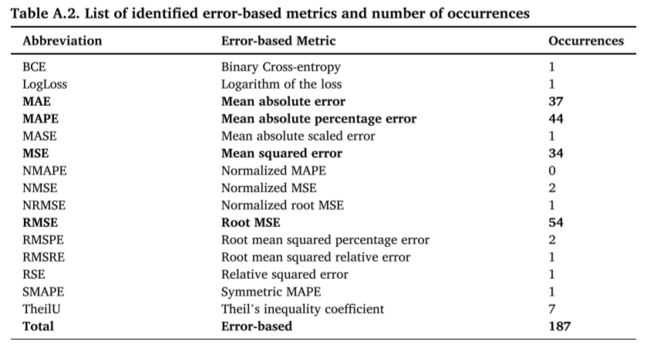
基于误差的指标:即通过计算真实收益和算法预测的收益之间的预测误差来估计算法的性能。主要包括MAE、MSE以及RMSE等。
基于准确性的指标:即将算法预测的收益类别与真实的类别进行比较,测量其准确性。主要包括Accuracy、F1、Recall以及 等。
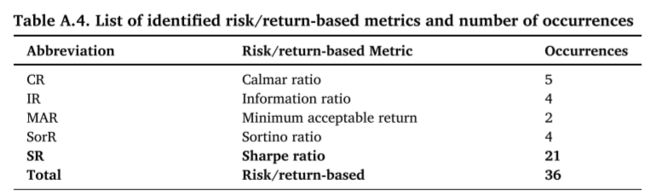
基于投资评估的指标:即用买入-持有-卖出信号评估由该算法提出的投资策略所得到的结果。主要包括夏普比率、最大回撤、索提诺比率等。
其他信息指标:考虑一些次要因素,比如交易的数量,持仓的天数,投资策略的成本,CPU/GPU时间等。
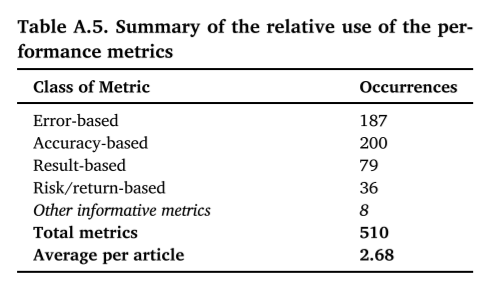
在统计的文章中,各类度量指标的使用频率如下面的表所示:
所有度量指标的总统计如下表所示:
3
实验验证
文中通过以下几种模型来展示不同度量指标的效果。模型包括:MLP、LSTM、ResNet、SVM以及XGBoost。用到了道琼斯指数中的28支股票进行验证,用到了20年的每日价格历史数据。其中,15年的用于训练算法,5年用于测试作为样本外数据。自变量包括前几天的Open、Close、High、Low价格和成交量以及14个技术指标和同一指数中其他股票的收盘价。算法接收当天的信息,并预测次日开盘时的收益。我们应用以下的投资策略:如果第二天的预期回报是正的,我们就进行开仓买入,否则我们就不开仓。每笔交易的成本设为0.10%。
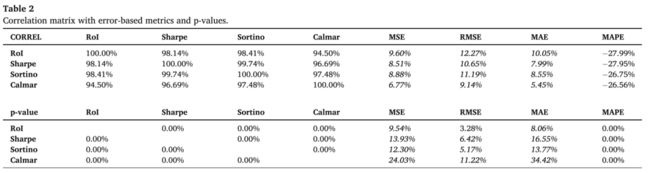
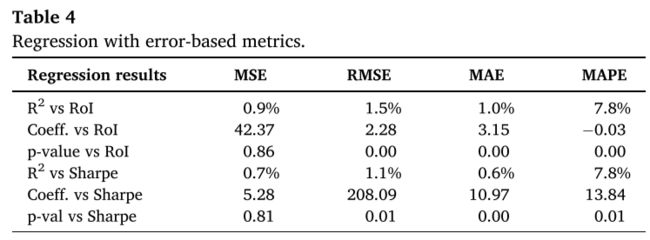
根据实验结果,文中首先研究基于回归误差的评估指标与其他风险指标之间的相关性,结果如下表所示:
正常来说,基于误差的指标应该与RoI、Sharpe、Sortino和Calmar比率呈负相关,即误差越小,回报越高。然而,根据Table 2的结果可以看到,只有MAPE和风险回报指标之间具有负相关关系且具有显著性差异。
除此之外,文中还比较了风险指标与基于准确率的指标之间的相关性,如下表所示:
同基于误差的指标一样,正常来讲,两者应该呈现负相关,也即是误差越小,回报越高。然而,从表中可以看出,R和R²与年回报率和风险/回报率呈负相关,但没有显著性差异。Accuracy、F1、Precision和Recall以及MCC与RoI以及Sharpe、Sortino和Calmar比率呈正相关,并且Accuracy和F1的相关性最高,MCC的相关性最低。
除此之外,文章还通过回归的方式探究了度量指标与Rol以及Sharpe之间的相关性。可以看出,在基于误差的度量指标中,只有MAPE表现出一定的相关性。在基于准确性的度量指标中,Accuracy、F1、Precision和Recall以及MCC都表现出了相关性。
因此,通过上面的实验分析得出下面的结论:
基于误差的度量指标,如R和R²并没有提供一个相对可靠的结果来改善投资策略,并且它们还会提供一些误导性的指示,所以实际中不应应用此指标。
Accuracy、F1、Recall或Precision和MCC为算法提供了一种相对合理以及可接受的结果,但与基于风险/回报的度量标准的效率相比还远远不够,而且经常无法确定表现最佳的算法。
Sharpe, Sortino或Calmar优于基于准确性的度量指标,因为它们从更多角度对结果进行了评估。然而,它们仍然存在一些问题,将在下一节中进行介绍。
4
提出的度量指标
夏普比率(Sharpe)在基于风险回报业绩指标中占据主导地位,远远领先于索蒂诺(Sortino)、卡尔马(Calmar)和信息比率等指标。Sharpe和Sortino比率有两个重要的问题:(i)它们都假设收益是高斯分布的,(ii)它们不允许在不同资产或不同时间段内比较不同算法的性能。所以,这篇文章中提出了一种新的度量指标,它改进了风险度量,并能够比较算法在不同时间和不同资产的效果。
为了解决这个问题,文中使用了一个新的性能指标,称之为D-ratio。为了构建这个D-ratio,将使用两个组成部分,包括(i)D-return:将比较算法与Buy&Hold策略的年回报率。(ii)D-VaR:将衡量算法与Buy&Hold策略的降低风险的相对能力。最终的D-ratio指标是D-return和D-VaR的结合。
一种简单的度量D-return的形式是算法与Buy&Hold策略的年化收益的比值,即:
为了解决两者收益结果可能存在符号不同的问题,D-return进行了如下改进,改进后的形式是:
如果D-return大于1,表示算法的表现优于Buy&Hold策略的表现;如果D-ratio小于1,表示算法的表现比Buy&Hold策略表现差。
接着,将算法的投资策略与Buy&Hold策略的风险使用CF-VaR进行比较,得到D-VaR,它的形式是:
进一步地,将D-return与D-VaR进行结合,得到D-ratio的表示形式:
当D-ratio为1时,算法与Buy&Hold策略可以带来相同的风险调整回报。如果D-ratio小于1,则该算法的表现低于Buy&Hold策略。如果D-ratio大于1,则算法的风险调整收益大于Buy&Hold策略。
文中提出的D-ratio有以下几点好处:
D-ratio不受收益高斯分布假设的限制,可以更好地反映风险情况;
D-ratio比率适用于所有类型的算法,包括ML、DL和RL以及各类回归或分类任务;
D-ratio比率对时间不敏感,因此可以对算法在不同的时间段进行比较。并且,通过测试完整周期与两个子周期的D-ratio,可以很容易地验证算法的稳定性;
D-ratio可以分解为一个D-return用于评估算法提高收益的效率,以及一个D-VaR,用于评估算法降低风险的效率。
D-ratio允许将算法的有效性与不同资产、同一资产类别或不同资产类别进行比较。
D-ratio允许将算法与只做多策略或卖空策略进行比较。它可以有效地衡量交易成本对算法有效性的影响,以提高投资策略的风险/回报;
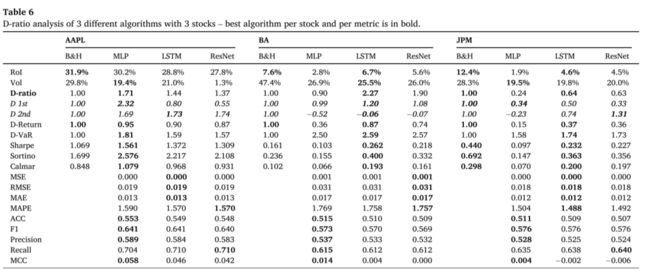
为了验证提出的D-ratio指标的有效性,文中用到了其中三支股票的数据进行了验证,并且将数据分为了两份D-1st和D-2nd用于评估策略的稳定性。实验的结果如下表所示:
从Table 6可以看出,没有一种算法是可以在两段时段上同时有效,并且同一种算法在三只股票上的表现也是不一样的。 并且,使用D-ratio指标可以研究为什么一种算法在一只股票上比在另一只股票上表现更好,并以及进行优化。除此之外,还证明了D-ratio在区分算法和衡量算法与Buy&Sell基准策略方面的有效性。
5
总结
当前的大多数文献使用基于误差或基于准确性的度量指标来构建交易模型,这些度量易于使用,但对被分析算法的性能进行评估的效率却很低,导致产生不可靠的结论。即使是其中效果较好的指标如夏普和索蒂诺比率,也会受到正态分布回报假设的影响。此外,它们没有衡量算法相对于Buy&Sell策略的关系。对此,这篇文章提出了另一种度量指标D-ratio,它衡量的是算法相对于Buy&Sell策略的表现,因此,D-ratio对时间不敏感,可以用来比较算法随时间或跨资产的表现。D-ratio使得评估算法的可靠性、重现性和稳定性成为可能,这是在实际应用中有效采用任何算法的先决条件。
参考文献:
Dessain, J. (2022). Machine learning models predicting returns: why most popular performance metrics are misleading and proposal for an efficient metric. Expert Systems with Applications, 116970.
关注《人工智能量化实验室》公众号,后台发送112可获取原论文。
Github:https://github.com/JDE65/D-ratio

了解更多人工智能与
量化金融知识
<-请扫码关注
让我知道你在看
![]()