一维FDTD电磁波仿真

一维FDTD电磁波Matlab仿真

1.1 时域有限差分法的基本方程

广义麦克斯韦方程（线性、均匀、各向同性)

​ $\Delta \times H=\epsilon \frac{\partial E}{\partial t}+{\sigma }^{e}E+J_i$ $(1.3a)$

​ $\Delta \times E=\mu \frac{\partial H}{\partial t}+{\sigma }^{m}E+M_i$ $(1.3b)$

${\sigma }^e$为电导率， $J_i$ 为施加电流密度， ${\sigma }^m$为导磁系数**（与电导率对应，非磁导率）**， $M_i$为施加磁流密度。

方程由两个矢量方程组成，在三维空间每个矢量可以分解为 3 个标量方程。因此麦克斯韦旋度方程可以表示为 6 个标量方程，在直角坐标系下，有

$\frac{\partial E_x}{\partial t}=\frac{1}{{\epsilon }_x}(\frac{\partial H_z}{\partial y}-\frac{\partial H_y}{\partial z}-{\sigma }_x^e{E}_x-J_{ix})$ $(1.4a)$

$\frac{\partial E_y}{\partial t}=\frac{1}{{\epsilon }_y}(\frac{\partial H_x}{\partial z}-\frac{\partial H_z}{\partial x}-{\sigma }_y^e{E}_y-J_{iy})$ $(1.4b)$

$\frac{\partial E_z}{\partial t}=\frac{1}{{\epsilon }_z}(\frac{\partial H_y}{\partial x}-\frac{\partial H_x}{\partial y}-{\sigma }_z^e{E}_z-J_{iz})$ $(1.4c)$

$\frac{\partial H_x}{\partial t}=\frac{1}{{\mu }_x}(\frac{\partial E_y}{\partial z}-\frac{\partial E_z}{\partial y}-{\sigma }_x^m{H}_x-M_{ix})$ $(1.4d)$

$\frac{\partial H_y}{\partial t}=\frac{1}{{\mu }_y}(\frac{\partial E_z}{\partial x}-\frac{\partial E_x}{\partial z}-{\sigma }_y^m{H}_y-M_{iy})$ $(1.4e)$

$\frac{\partial H_z}{\partial t}=\frac{1}{{\mu }_z}(\frac{\partial E_x}{\partial y}-\frac{\partial E_y}{\partial x}-{\sigma }_z^m{E}_z-M_{iz})$ $(1.4f)$

FDTD 的计算，首先用有限差分来近似麦克斯韦方程中的空间和时间导数；其次构造一组方程，以前一时间步瞬时场值来计算后一时间步瞬时场值，由此来构造时间向前推进的算法，以模拟电磁场在时域的进程。

1.1.1 导数的差分近似

前向差分公式（一阶精度）

$f’(x)\simeq \frac{f(x+\Delta x)-f(x)}{\Delta x}$ $(1.6)$

后向差分公式（一阶精度）

$f’(x)\simeq \frac{f(x)-f(x-\Delta x)}{\Delta x}$ $(1.7)$

中心差分公式（二阶精度）

$f’(x)\simeq \frac{f(x+\Delta x)-f(x-\Delta x)}{2\Delta x}$ $(1.8)$

虽然文献中有基于高阶精度差分公式的 FDTD 算法，但常规的 FDTD 算法是基于有二阶精度的中心差分公式的算法，这种算法在大多数电磁应用中精度是足够的，具有编程简单、易于理解的特点。

1.2 一维问题的 FDTD 更新方程

在一维情况下，场分布与另两个坐标变量无关。例如，如果研究 $x$ 坐标轴上的一维问题，则在麦克斯韦两个旋度方程中对 $y,z$的导数就为零。因此旋度方程 (1.4) 可重写为

​ $\frac{\partial E_x}{\partial t}=\frac{1}{{\epsilon }_x}(-{\sigma }_x^e{E}_x-J_{ix})$ $(1.a39)$

​ $\frac{\partial E_y}{\partial t}=\frac{1}{{\epsilon }_y}(-\frac{\partial H_z}{\partial x}-{\sigma }_y^e{E}_y-J_{iy})$ $(1.39b)$

​ $\frac{\partial E_z}{\partial t}=\frac{1}{{\epsilon }_z}(\frac{\partial H_y}{\partial x}-{\sigma }_z^e{E}_z-J_{iz})$ $(1.39c)$
​ $\frac{\partial H_x}{\partial t}=\frac{1}{{\mu }_x}(-{\sigma }_x^m{H}_x-M_{ix})$ $(1.39d)$

​ $\frac{\partial H_y}{\partial t}=\frac{1}{{\mu }_y}(\frac{\partial E_z}{\partial x}-{\sigma }_y^m{H}_y-M_{iy})$ $(1.39e)$

​ $\frac{\partial H_z}{\partial t}=\frac{1}{{\mu }_z}(-\frac{\partial E_y}{\partial x}-{\sigma }_z^m{E}_z-M_{iz})$ $(1.39f)$

注意方程 (1.39a) 和 (1.39d) 仅包含对时间的导数而不包含对空间的导数，因此这些方程不代表传播场，场分量 $E_x$与 $H_x$ 仅存在在方程中而不传播。其他四个方程代表传播场，四个方程中的电场和磁场对于 $x$ 轴均为横向场，因此在一维情况下存在 TEM 波。

方程 (1.39b) 与 (1.39f) 仅含 $E_y$ 与 $H_z$ 两项，方程 (1.39c) 与 (1.39e) 仅含 $E_z$ 与$H_y$两项，两组方程可以分开研究。

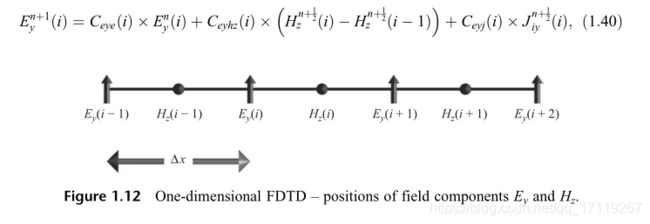
（1）电场 $y$ 分量更新方程

$E_y^{n+1}(i)=C_{eye}(i)\times E_y^n(i)+C_{eyehz}(i)\times (H_z^{n+1/2}(i)-H_z^{n+1/2}(i-1))+C_{eyj}(i)\times J_{iy}^{n+1/2}(i)$ (1.40)

式中

$C_{eye}(i)=\frac{2{\epsilon }_y(i)-\Delta t{\sigma }_y^e(i)}{2{\epsilon }_y(i)+\Delta t{\sigma }_y^e(i)}$

$C_{eyhz}(i)=-\frac{2\Delta t}{(2{\epsilon }_y(i)+\Delta t{\sigma }_y^e(i))\Delta x}$

$C_{eyj}(i)=-\frac{2\Delta t}{2{\epsilon }_y(i)+\Delta t{\sigma }_y^e(i)}$

（2）磁场 $z$ 分量更新方程

$H_z^{n+1/2}(i)=C_{hzh}(i)\times H_z^{n-1/2}(i)+C_{hzey}(i)\times (E_y^n(i+1)-E_z^n(i))+C_{hzm}(i)\times M_{iz}^n(i)$ (1.41)

式中

$C_{hzh}(i)=\frac{2{\mu }_z(i)-\Delta t{\sigma }_z^m(i)}{2{\mu }_z(i)+\Delta t{\sigma }_z^m(i)}$

$C_{hzey}(i)=-\frac{2\Delta t}{(2{\mu }_z(i)+\Delta t{\sigma }_z^m(i))\Delta x}$

$C_{hzm}(i)=-\frac{2\Delta t}{2{\mu }_z(i)+\Delta t{\sigma }_z^m(i)}$

（3）电场 $z$ 分量更新方程

$E_z^{n+1}(i)=C_{eze}(i)\times E_z^n(i)+C_{ezhy}(i)\times (H_y^{n+1/2}(i+1)-H_y^{n+1/2}(i))+C_{ezj}(i)\times J_{iz}^{n+1/2}(i)$ (1.42)

式中

$C_{eze}(i)=\frac{2{\epsilon }_z(i)-\Delta t{\sigma }_z^e(i)}{2{\epsilon }_z(i)+\Delta t{\sigma }_z^e(i)}$

$C_{ezhy}(i)=-\frac{2\Delta t}{(2{\epsilon }_z(i)+\Delta t{\sigma }_z^e(i))\Delta x}$

$C_{ezj}(i)=-\frac{2\Delta t}{2{\epsilon }_z(i)+\Delta t{\sigma }_z^e(i)}$

（4）磁场 $y$ 分量更新方程

$H_y^{n+1/2}(i)=C_{hyh}(i)\times H_y^{n-1/2}(i)+C_{hyeh}(i)\times (E_z^n(i+1)-E_z^n(i))+C_{hym}(i)\times M_{iy}^n(i)$(1.43)

式中

$C_{hyh}(i)=\frac{2{\mu }_y(i)-\Delta t{\sigma }_y^m(i)}{2{\mu }_y(i)+\Delta t{\sigma }_y^m(i)}$

$C_{hyez}(i)=-\frac{2\Delta t}{(2{\mu }_y(i)+\Delta t{\sigma }_y^m(i))\Delta x}$

$C_{hym}(i)=-\frac{2\Delta t}{2{\mu }_y(i)+\Delta t{\sigma }_y^m(i)}$

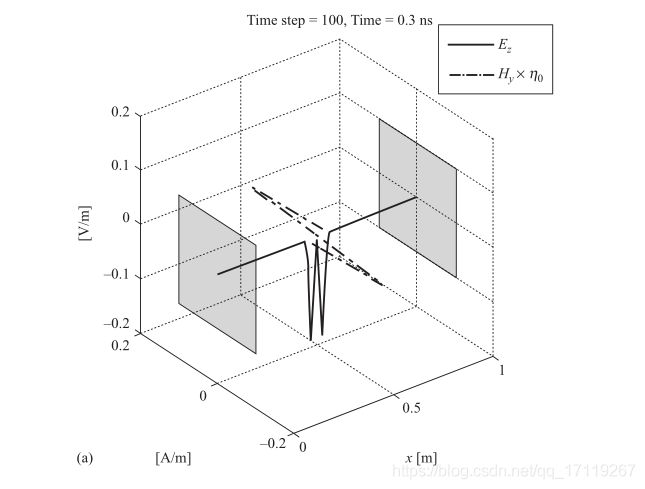
附录 A 的代码给出了基于式 (1.42) 与式 (1.43) 的一维 FDTD MATLAB 仿真程序。程序计算了由 $z$ 向电流屏 $J_z$ 所产生的电场与磁场，电流屏与两个理想导电平面平行并处于二者中间，其他空间区域填充以空气。两导电平面间距 $1m$，空间步长 $\Delta x=1mm$ ，电流屏电流密度为 $1A/m^2$ ，按照高斯函数随时间变化

$J_z(t)=e^{-(\frac{t-2\times 10^{-10}}{5\times 10^{-11}}{)}^2}$

激励源电流屏厚度 $1mm$ ，可将 $J_z$ 转换为表面电流密度 $K_z$ ，大小为 $1\times 10^{-3}A/m^2$ 。该激励源在屏两侧产生磁场，幅度为 $5\times 10^{-4}A/m$ 。为场在自由空间中传播，故产生的电场为 ${\mu }_0\times 5\times 10^{-4}=0.1885V/m$ ，其中${\mu }_0\backsimeq 337\Omega$ 。

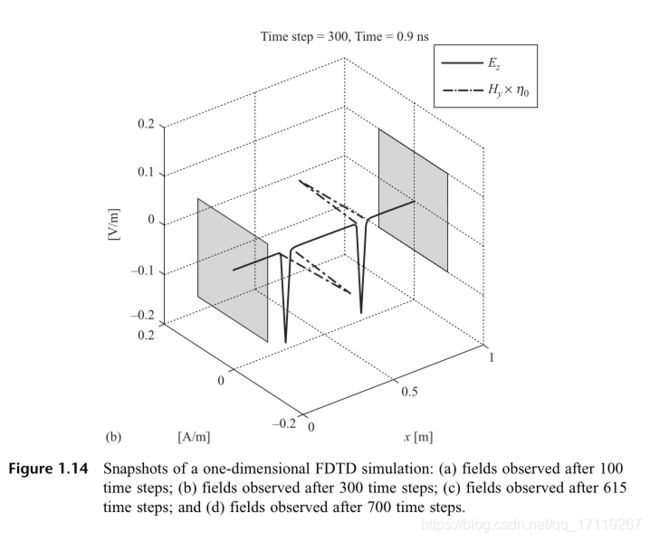
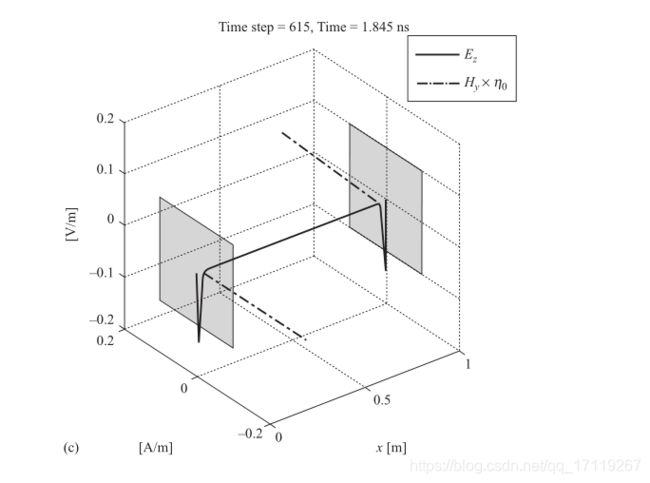
​ 程序中有几点值得注意：其一为电场存储数组比磁场存储数组多一个节点，这是因为电场和磁场在离散化后交叉分布的结果（图 1.12 与 图 1.13）；其二，两端理想导电平面上需要设置边界条件，即 $E_z=0$ ；其三，如结果图 1.14 所示，场量经理想导电平面反射后，电场方向点到，代表反射系数为 1，磁场方程不变，表示反射系数为 -1。

一维 FDTD 问题 MATLAB 仿真程序

算法流程图:

主程序 fdtd1D.m

% This program demonstrates a one-dimensional FDTD simulation
% The problem geometry is composed of two PEC plates extending to 
% infinity in y, and z dimensions, parallel to each other with 1 meter
% separation The space between the PEC plates is filled with air
% A sheet of current source parallel to the PEC plates is placed
% at the center of the problem space. The current source excites fields
% in the problem space due to a z-directed current density Jz,
% which has a Gaussian waveform in time.

clc, clear, close all;

% Define initial constants
eps_0  =  8.854187817e-12;                % permittivity of free space
mu_0   =  4 * pi * 1e-7;                  % permeability of free space
c      =  1 / sqrt(mu_0 * eps_0);         % speed of light


% Define problem geometry and parameters
domain_size = 1;                          % 1D problem space length in meters
dx = 1e-3;                                % cell size in meters
dt = 3e-12;                               % duration of time step in seconds
number_of_time_steps = 1000;              % number of iterations
nx = round(domain_size / dx);             % number of cells in 1D problem space
source_position = 0.5;                    % position of the current source jz


% Initialize field and material arrays
Ceze      = zeros(nx+1,1);
Cezhy     = zeros(nx+1,1);
Cezj      = zeros(nx+1,1);
Ez        = zeros(nx+1,1);
Jz        = zeros(nx+1,1);
eps_r_z   = ones(nx+1,1);                 % free space
sigma_e_z = zeros(nx+1,1);                % free space

Chyh      = zeros(nx,1);
Chyez     = zeros(nx,1);
Chym      = zeros(nx,1);
Hy        = zeros(nx,1);
My        = zeros(nx,1);
mu_r_y    = ones(nx,1);                   % free space
sigma_m_y = zeros(nx,1);                  % free space


% Calculate FDTD updating coefficients
Ceze  = (2 * eps_r_z * eps_0 - dt * sigma_e_z)...
      ./ (2 * eps_r_z * eps_0 + dt * sigma_e_z);

Cezhy = (2 * dt / dx) ...
      ./ (2 * eps_r_z * eps_0 + dt * sigma_e_z);
  
Cezj  = (-2 * dt) ...
      ./ (2 * eps_r_z * eps_0 + dt * sigma_e_z);
  
Chyh  = (2 * mu_r_y * mu_0 - dt * sigma_m_y) ...
      ./ (2 * mu_r_y * mu_0 + dt * sigma_m_y);
  
Chyez = (2 * dt / dx) ...
      ./ (2 * mu_r_y * mu_0 + dt * sigma_m_y);
  
Chym  = (-2 * dt) ...
      ./ (2 * mu_r_y * mu_0 + dt * sigma_m_y);

  
% Define the Gaussian source wavefront
time         = dt * [0 : number_of_time_steps - 1];
Jz_waveform = exp( - (( time - 2e-10) / 5e-11 ).^2);
source_position_index = round(nx * source_position / domain_size) + 1;


% Subroutine to initialize plotting
initialize_plotting_parameters;


% FDTD loop
for time_step = 1:number_of_time_steps
    
    % Update Jz for the current time step
    Jz(source_position_index) = Jz_waveform(time_step);
    
    % Update magnetic field
    Hy(1:nx) = Chyh(1:nx) .* Hy(1:nx) ...
             + Chyez(1:nx) .* (Ez(2:nx+1) - Ez(1:nx)) ...
             + Chym(1:nx) .* My(1:nx);
    
    % Update electric field
    Ez(2:nx) = Ceze(2:nx) .* Ez(2:nx) ...
             + Cezhy(2:nx) .* (Hy(2:nx) - Hy(1:nx-1)) ...
             + Cezj(2:nx) .* Jz(2:nx);
         
   Ez(1)     = 0; % Apply PEC boundary condition at x = 0 m
   Ez(nx+1)  = 0; % Appky PEC boundary condition at x = 1 m
   
   % Subroutine to plot the current state of the fields
   plot_fields;
end

初始化绘图参数 initialize_plotting_parameters.m

% subroutine used to initialize 1D plot

Ez_positions = [0:nx] * dx;
Hy_positions = ([0:nx - 1] + 0.5 ) * dx;
v = [0 -0.1 -0.1; 
     0 -0.1 0.1; 
     0 0.1 0.1;
     0 0.1 -0.1;
     1 -0.1 -0.1;
     1 -0.1 0.1;
     1 0.1 0.1;
     1 0.1 -0.1];
 f = [1 2 3 4; 5 6 7 8];
 axis([0 1 -0.2 0.2 -0.2 0.2]);
 lez = line(Ez_positions, Ez*0, Ez, 'Color', 'b', 'LineWidth', 1.5);
 lhy = line(Hy_positions, 377*Hy, Hy*0, 'Color', 'r', 'LineWidth', 1.5, ...
        'linestyle', '-');
 set(gca, 'fontsize', 12, 'FontWeight', 'bold');
 axis square;
 legend('E_{z}', 'H_{y}_\times_377', 'Location', 'NorthEast');
 xlabel('x_{m}');
 ylabel('[A/m]');
 zlabel('[V/m]');
 grid on;
 p = patch('vertices', v, 'faces', f, 'facecolor', 'g', 'facealpha', 0.2);
 text(0, 1, 1.1, 'PEC', 'horizontalalignment', 'center', 'fontweight', 'bold');
 text(1, 1, 1.1, 'PEC', 'horizontalalignment', 'center', 'fontweight', 'bold');

绘制图片 plot_fields.m

% subroutine used to plot 1D transient fields
delete(lez);
delete(lhy);
lez = line(Ez_positions, Ez*0, Ez, 'Color', 'b', 'LineWidth', 1.5);
lhy = line(Hy_positions, 377*Hy, Hy*0, 'Color', 'r', 'LineWidth', 1.5, ...
        'linestyle', '-');
ts = num2str(time_step);
ti = num2str(dt * time_step * 1e9);
title(['time _ step  = ' ts ', time =  ' ti ' ns']);
drawnow;

参考书籍：The Finite-Difference Time-Domain Method For Electromagnetics with MATLAB Simulations by Atef Z. Elsherbeni, Veysel Demir