强化学习基础概念详解

Reinforcement Learninig

1.基础数学概念

1.1随机变量

概率论方面：

随机变量：随机变量是一个未知的量，它只取决于一个随机事件的结果，比如我抛一个硬币，朝上记为零，朝下记为1，抛硬币是一个随机事件，抛硬币的结果记为一个随机变量X（大写字母表示）,随机变量有两种取值0/1,抛硬币前，我是不知道X的值是什么，但是我知道这个随机事件的概率均为0.5

通常用小写字母表示对随机变量的观测值，概率统计通常用大小写来区分随机变量和观测值，观测值是什么意思呢？当随机事件结束。会观测到硬币的哪一面朝上，这个观测值就几位小x,就是一个数，没有随机性，于是得到了4个观测值x_1 = 1, x_2 = 1, x_3 = 0, x_4 = 1.这四个数就是随机变量的观测值。

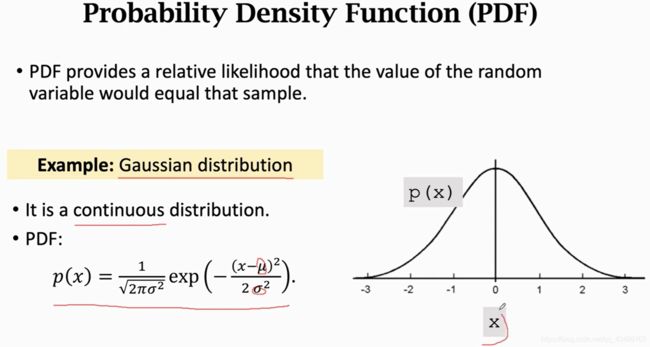
1.2概率密度函数

概率密度有什么物理意义呢？

它意味着随机变量在某个确定的取值点附近的取值性

高斯概率密度函数分布是这个样子，图像横轴随机变量取值，纵轴概率密度，曲线就是高斯分布的概率密度曲线，说明x在原点附近的取值比较大，远离原点的地方取值较小。

离散概率密度，随机变量为离散，

概率密度函数的性质：随机变量的定义域记为_x_,如果_p_是一个连续的概率分布，可以对_p(x)_做定积分，结果为1，把所有可能的结果都算上。

1.3期望

1.4随机抽样

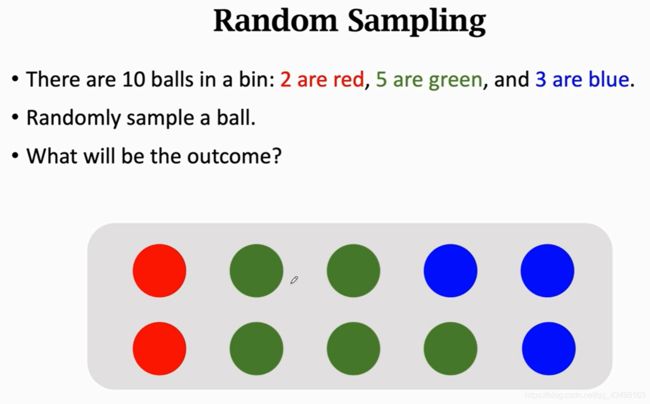
随机摸出来一个球，三种颜色都有可能，概率分别为0.2，0.5，0.3，现在真的摸出来一个，睁开眼就一个是红色，那这个红色就是观测值，这个过程就叫随机抽样。

换一种问法：现在箱子里有很多的球，

我也不知道有多少个，随机抽样，抽到红色球的概率是0.2，绿色球的概率0.5，蓝色球的概率0.3，把手伸进箱子，摸一个球，摸到球的颜色是什么样的呢？跟刚才的一样。

现在随机摸一个放回，打散后重新摸，一共重复100次，记录下来的颜色有什么特点，这个就具有统计意义了，20红，30绿，30蓝。

【一定要深刻理解随机抽样，强化学习这一块反复用到，随后我会具体解释】

2.强化学习概念理解

强化学习很难的关键地方首先就是对其专业术语的理解，Terminologies，名词如果记不住的话真的完全看不懂文章，因此只能把这些专业术语都记住，都理解。

2.1 State and Action

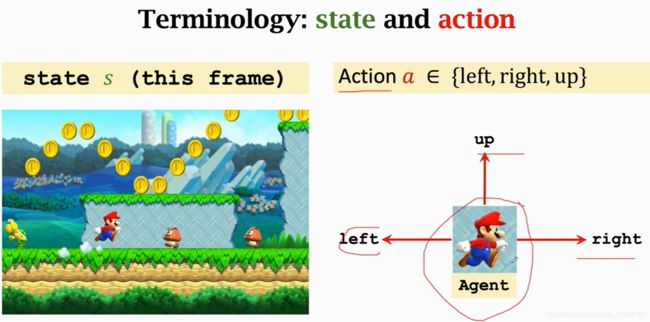
State:状态，状态啥意思呢？ 假设你在玩超级玛丽游戏，你可以认为此时的状态就是屏幕中的一副画面（不严谨），你玩游戏时观察到上面的状态，你就可以做出反应，此时我的agent应该采取什么动作。

Action: 左右上，就是动作， 动作是谁做的，谁就是agent

2.2 Policy

什么是policy策略，你观察到屏幕上这张画面时，你该让agent采取什么动作呢，往上下还是左----

policy: 根据观察到状态，做出决策，控制agent运动

在数学上policy函数是这么定义的, π是一个概率密度函数，π(a|s)= P(A=a|S=s}给定状态S所属的动作A的概率密度函数

如图，观察到这张图片，agent可以做出三种动作中的一种，把这张图片输入policy π, 会告诉你向左的概率0.2，向右概率0.1，向上概率0.7，如果你让这个policy函数自动来操作，它就会做一个随机抽样，以0.1的概率向右，0.7的概率向上，0.2的概率向左，三种动作都有可能发生，但是向上的概率最大。

强化学习学什么？就是学这个policy

为什么要让动作随机呢? 超级马丽里面这个agent不管动作是确实还是随机都没有问题，但如果是跟人博弈最好还是要随机，要是你的动作很确定，别人就有办法赢，石头剪子布时，如果你的策略确定，那就有规律可寻了，对手就能猜到你下一步出什么，你肯定输，只有你时随机的，别人猜不出来，你才有可能赢。所以很多应用里面policy最好是一个概率密度函数，动作最好时随机抽样得到，要有随机性。

2.3 Reward

agent做出一个动作，环境就会给一个奖励，这个奖励通常需要我们来定义，奖励定义的好坏非常影响强化学习的结果，怎么样定义奖励就是仁者见仁智者见智了，例如agent吃一个金币奖励就是+1,赢了这场游戏奖励就是+10000，打赢游戏的奖励应该大些，这样学到的policy才是答应游戏，而不是一味的吃金币，如果碰到敌人挂了那就是-10000，如果啥也没有发生奖励就是0，强化学习的总目标呢就是获得的奖励要高

2.4 State Transition

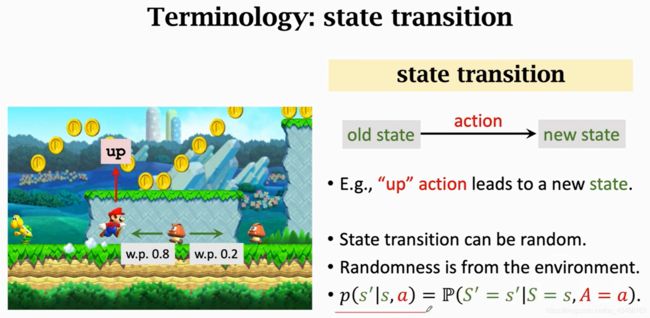
状态转移，当前状态下agent做一个动作，环境就会给一个新的状态，

比如agent跳一下画面的下一个状态就变了，这个过程就叫做状态转移

状态转移可以是确定的也可以是随机的，通常认为状态转移时随机的，结合Marlov链状态转移的随机性很好理解，状态转移的随机性是从环境里来的，环境是什么呢，环境就是游戏的程序，游戏程序决定下一个状态是什么，举例说明状态转移的随机性，如果agent向上跳，agent的位置就像上来了，这个位置的确定的，但是敌人可能往左也可能往右这个随机的，这就造成了下一个状态的随机性。

可以把状态转移函数用_p_函数表示这是个条件概率密度函数，，状态采取动作a到下一个s_的概率，注意这个状态转移函数，只有环境自己知道，因为比如敌人向左向右都是概率事件，这个也是最开始我一直没明白为什么已经做了确定动作为什么到下个状态还是概率

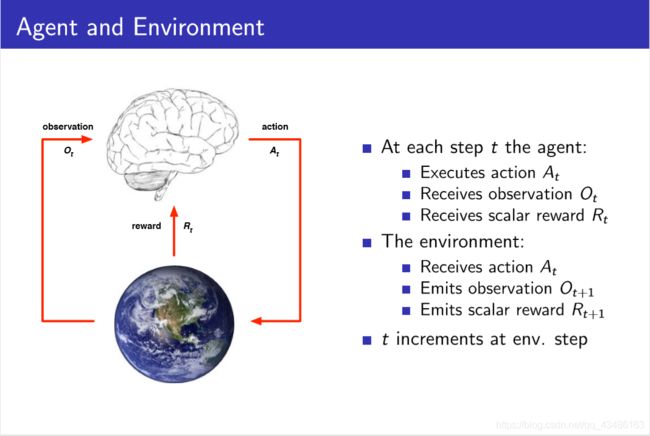
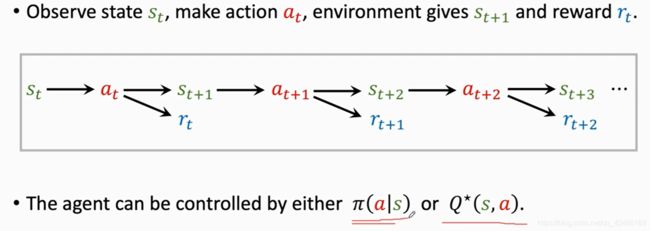
2.5 Agent environment interaction

2.6 Randomness in RL

理解强化学习的随机性，搞清楚两个来源，对后面理解算法很有帮助。

第一个随机性来源于动作，动作是根据policy函数随机抽样得到的，用policy函数来控制agent,给定当前状态s，agent的动作A是根据policy函数输出的概率来随机抽样，比如说当前观测的状态S，policy函数会告诉每个动作的概率有多大，左0.2，右0.1，上0.7,所以agent可能做其中任何一种动作，但动作的概率有大有小

另一个随机性来源是状态转移，如图agent做出了a的动作，那么环境就会生成一个s‘_，这个状态s‘具有随机性，环境用状态转移函数p算出概率，然后用概率来随机抽样得到下一个状态s’，

怎么样用AI来自动答应游戏？

通过强化学习学到policy函数 π，观测到游戏当前的这一帧状态s_1,AI用policy函数来算一个概率，然后**随机抽样的到动作a_1，然后环境又会生成下一个状态s_2，并且给agent一个奖励r_1-----------知道打赢游戏得到一个trajectory。

2.7 Rewards and Returns

未来的累计奖励，把t时刻的奖励记为Gt,把t时刻的奖励全部加起来，一直加到游戏结束，由于Rt和Rt+1，并不是同样重要的，举个例子，现在给你100块和未来给你100块，你选择哪一个，肯定会立刻选择得到这100块，未来的100块搞不好就是画饼，未来的不确定性很大，换一个问法：**现在立刻给你80块钱，和未来给你100块钱，你选择哪一个？**那就啥选择都有了，所以未来的100块奖励不如现在的好！未来的100恐怕就值现在的80！，因此应该给未来的奖励打一个折扣，后面的权重应该更低才可以

因为未来的奖励没有现在的奖励值钱，因此强化学习引入折扣因子gamma [0, 1] 折扣率是个超参数需要自己来调。

Return的随机性

观察如图所示，如果游戏此时为t已经结束了，那么这个时候的所有的奖励R都已经观测到了，那么奖励就都是数值，用小写字母表示，如果在t时刻还没有结束，那么这些奖励R还有事随机变量，没有被观测到，我们就用大写字母来表示

由于奖励G依赖于奖励R，所以Return G也是一个随机变量！

那么由于R与S，A都有关，因此从t时刻起，Return就与所有的后续状态以及动作都有关了。

2.8 Value Functions

我们获得了回报Gt(因为参考了几个ppt所以对于回报的字母不一样，还是统一以Sutton的为准)，是未来奖励的总和，为啥要定义Return，因为非常有用，我们agent的目标就是它越大越好，除此之外，知道了Gt,我就知道了这局游戏我是快赢了还是快输了，Gt只是一个随机变量，t时刻你并不知道Gt是什么，打个比方你抛硬币，正1反0，t时刻你还没有把硬币抛出去，你并不知道你会得到1还是0，记住Gt是一个随机变量，它依赖与后续的At,At+1----和St,St+1------，那么由于Gt是一个随机变量，在t时刻我并不知道Gt是什么，那么我该怎么样评估当前的形式呢？

我们可以对Gt求期望，把里面的随机性性用积分都给积掉，得到的就是一个实数，例如抛硬币，你知道期望就是0.5，

同样对随机变量Gt求期望，可以得到一个数记作Q_pai，这个期望怎么求得呢？

把Gt当作未来所有动作A和S的一个函数，未来的动作A和状态S都有随机性，A的概率密度函数是π，S的概率密度函数是p,期望就是对未来的动作和状态求的，把这些随机变量都用积分给积掉，除了St和At，t+1，t+2----的都被积掉了，求期望后的函数被称为Qpi（St,At）,只与当前的动作和状态有关，因为后面的都被积掉了！St和At没有被积掉，作为观测值被观测到，而不是作为随机变量，Qpi的值依赖于他俩，还与π有关，因为

积分的时候会用到policy函数，如果π不一样，积分得到的Qpi就不一样

那么动作价值函数直观上有啥意义呢？

函数Qπ告诉我们，如果用policy函数π，那么在状态St下，做做动作At是好还是坏。因为π会给当前状态下所有动作打分，就知道那个动作好和不好

那么怎么样去掉Qπ，中的π呢？

可以对Qπ中的π求最大化，意思是我们可以有无数种policy π,但是我们应该使用最好的那一种π，把Q^ 称为最优动作价值函数，Q^ 与 π无关，因为π已经被去掉了，Q^有啥直观意义呢？

可以用来对动作a做评价，此可状态St，这个时候动作At好不好，比如下围棋时，状态就是这个棋盘，Q^ 告我我们如果把棋子放在这个位置胜算有多大，Q^ 非常有用，因为有了它，agent就可一个根据它对动作的评价做决策，观察到一个状态，如果Q^认为往上跳分数最高，agent就应该往上跳，

最后一个State-Value function 状态价值函数Vπ

它是关于Qπ的期望，把动作A作为随机变量，然后关于A求期望，把A消掉，求导的Vπ只跟π和St有关，Vπ有什么直观的意义呢？

Vπ可以告诉我们当前的局势好不好，假如我用policyπ下围棋，让Vπ来看看，我的胜算有多大，

这里的随机变量是关于A求的，A的概率密度函数是π，根据期望的定义，离散是加，连续是积分，如果动作都是离散的比如上下左右，就可以把期望写成连加
如果动作是连续的，比如自动驾驶汽车方向盘的角度-90-+90

3.强化学习自动打游戏

3.1 AI如何控制agent

假设我们以超级玛丽游戏为例，假设我们的目标是操作agent多吃金币，避开敌人往前走，打败敌人，通关每一关游戏，我们写个程序让AI来控制agent，我们应该怎么做？

一种办法是学习一个policy函数π，这个在RL里叫Policy based learning-策略学习，后面再详细扯这个，假设我们有个π，我么就可以用π来控制动作了，老规矩，给一个观测状态St,π产生每n一个动作的概率，然后**用这个概率来做一个随机抽样，**得到At,最后Agent执行这个动作。

第二种方法是我们有了最优动作价值函数Q*，在RL里叫做Value baesd learning-价值学习后面再详细扯这个，我们假如有个Q*，在St状态下，采取At动作是好还是坏，每观测到一个状态St，就把St作为 Q* 函数的输入，让Q* 对每一个动作都给一个评价，那就知道每一个动作的Q值，选择最大的。

3.2 Gym

传统经典控制

Atari 小时候玩小霸王的那种

连续控制问题，可以模拟物理量等，

如果你设计的RL算法，你怎么知道你的算法比别人还还是坏呢？

在标准数据集上测试效果比如GYM

3.2.1 怎么样使用gym

第一步重置reset，然后开始循环，每一轮能够还原，每一轮里agent做一个动作，环境会更新状态，给出奖励，

env.render() # 是渲染，把游戏里的发生展示给人看，
action = env.action_space.sample() # 随机均匀的抽样一个动作，记为action，实际上不应该均匀抽样
step(action)  # 真正执行这个动作

小结1