机器学习基础学习-过拟合和欠拟合
前言
上一篇博客有说到,通过多项式回归,我们可以对非线性的数据进行拟合,进而求解回归问题,但是过度使用多项式回归的方式,会牵扯到过拟合和欠拟合。
1、准备工作
还是先准备我们的数据集
# 过拟合与欠拟合
import numpy as np
import matplotlib.pyplot as plt
# 生成随机数据
# random.uniform(x, y)方法将随机生成一个实数,它在 [x,y] 范围内。
x = np.random.uniform(-3, 3, size = 100)
X = x.reshape(-1, 1) # shape:(100,1)
# np.random.normal()正态分布的噪音
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size = 100)
# 绘制样本
plt.scatter(x, y)
plt.show()
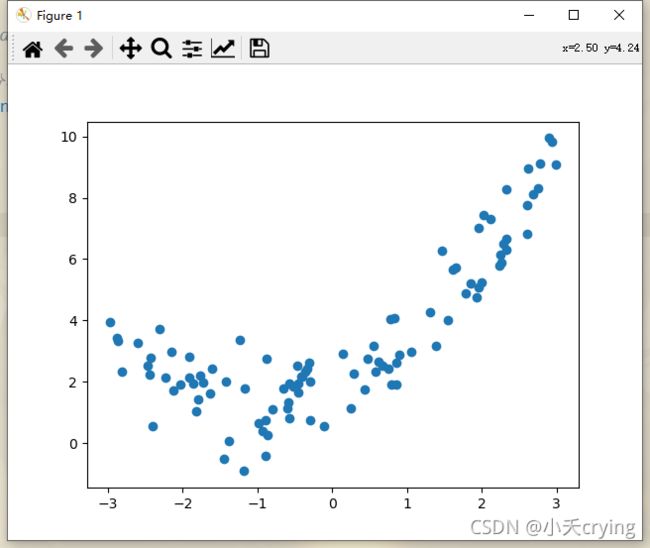
在机器学习基础学习-多项式回归中有提到用线性回归的方式拟合这些数据。但明显这样的拟合效果是不尽人意的。
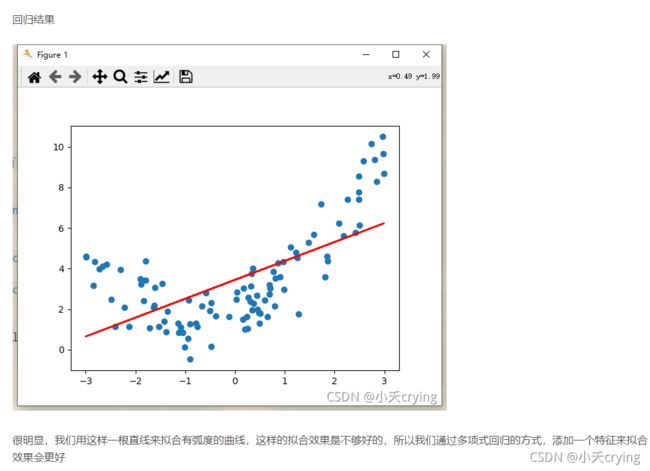
我们的多项式回归的本质其实只是增加了x的特征,但是本质上依旧是线性回归。
(1)均方误差衡量线性回归
首先对于直接用线性回归的方式进行拟合,我们训练一下,然后采用sklearn的mean_squared_error,用均方差衡量误差
from sklearn.linear_model import LinearRegression # 引入线性回归类对象
from sklearn.metrics import mean_squared_error # 引入均方误差
'''
线性回归拟合二次函数
'''
# 实例化对象
lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_predict = lin_reg.predict(X)
print('线性回归预测与真值的均方误差', mean_squared_error(y, y_predict))
![]()
(2)均方误差衡量多项式回归
这里还是调用上一篇博客机器学习基础学习-scikit-learn中的多项式回归和pipeline通过pipeline包装管道实现多项式回归
'''
多项式回归拟合二次函数
'''
# 包装管道进行多项式回归(传入degree,返回多项式回归的类)
def polynomialRegression(degree):
# 使用pipeline创建管道,送给poly_reg对象的数据会沿着管道的三步依次进行
return Pipeline([ # Pipeline传入的是列表,列表中传入管道中每一步对应的类(这个类以元组的形式进行传送)
("poly", PolynomialFeatures(degree=degree)), # 第一步:求多项式特征,相当于poly = PolynomialFeatures(degree=2)
("std_scaler", StandardScaler()), # 第二步:数值的均一化
("lin_reg", LinearRegression()) # 第三步:进行线性回归操作
])
poly2_reg = polynomialRegression(2)
# 将X送给poly_reg执行前两步操作,得到的全新的数据x会送给LinearRegression进行fit相应的操作
poly2_reg.fit(X, y)
y2_predict = poly2_reg.predict(X)
print('多项式回归预测与真值的均方误差', mean_squared_error(y, y2_predict))
![]()
对比使用线性回归的均方误差
![]()
使用多项式回归的均方误差,显然比使用线性回归的均方误差要小。
2、过拟合
我们通过pipeline封装了多项式回归的方法,并且设置了degree=2,绘制图形发现拟合效果比较好,并且均方误差比线性回归的均方误差要小。但是接下来改变degree的值。
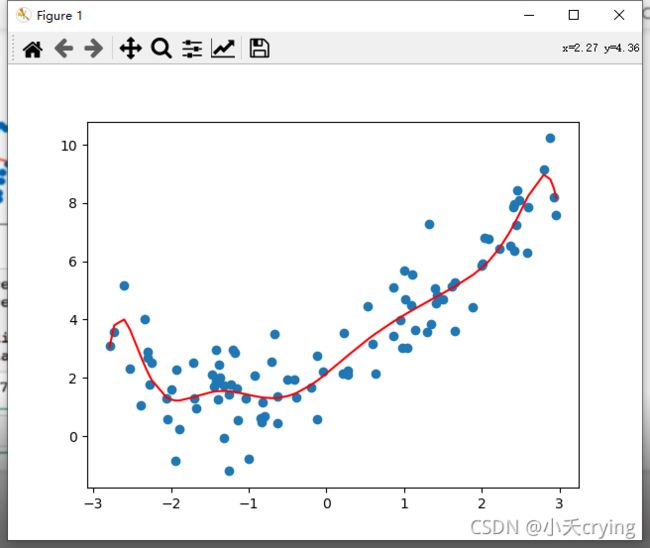
degree=10
''' degree= 10 '''
poly10_reg = polynomialRegression(10)
# 将X送给poly_reg执行前两步操作,得到的全新的数据x会送给LinearRegression进行fit相应的操作
poly10_reg.fit(X, y)
y10_predict = poly10_reg.predict(X)
print('degree=10多项式回归预测与真值的均方误差', mean_squared_error(y, y10_predict))
# 绘制预测后的结果
plt.scatter(x, y)
plt.plot(np.sort(x), y10_predict[np.argsort(x)], color='r')
plt.show()
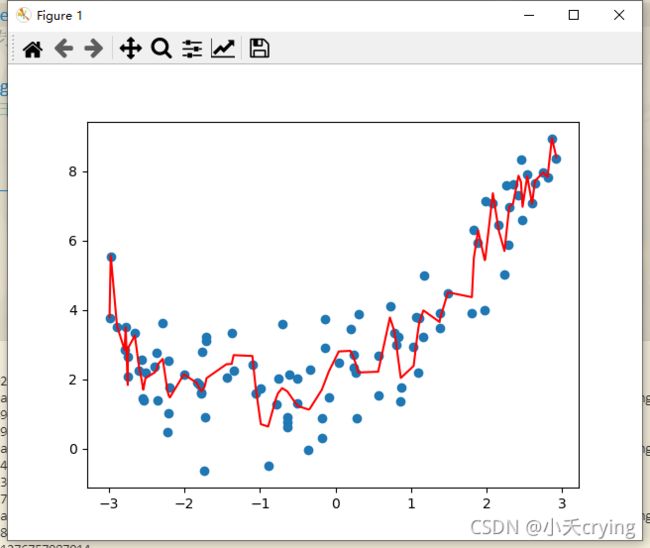
发现degree=10时比degree=2时的均方误差更小,并且绘制出图形,说明将degree传入10之后,训练出来的模型,对于原始的数据来说,比传入2时的效果要更加好。
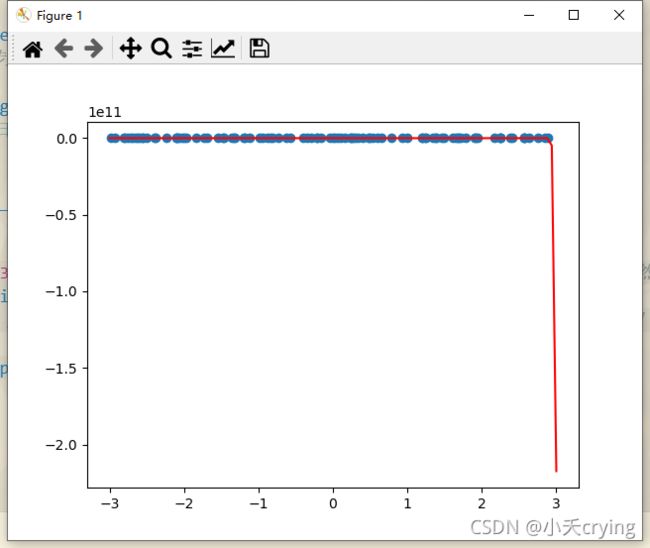
degree=100
进一步加大degree的值,直接令其等于100.
''' degree= 100 '''
poly100_reg = polynomialRegression(100)
# 将X送给poly_reg执行前两步操作,得到的全新的数据x会送给LinearRegression进行fit相应的操作
poly100_reg.fit(X, y)
y100_predict = poly100_reg.predict(X)
print('degree=10多项式回归预测与真值的均方误差', mean_squared_error(y, y100_predict))
# 绘制预测后的结果
plt.scatter(x, y)
plt.plot(np.sort(x), y100_predict[np.argsort(x)], color='r')
plt.show()
再次对比均方误差的值

绘制出图形
degree=100比之前degree=2、degree=10的均方误差更小了。并且图形的弯曲程度更厉害了(更加拟合原始数据),但这个时候绘制出来的图像其实并不是我们计算出来的拟合曲线,这个曲线只是我们通过预测值对应的点进行连接起来的结果,但是很多地方其实没有这个点,所以连接的曲线和原来的曲线不一样,我们换一种绘制方式,在(-3,3)均匀取值,这样不会出现两个点之间相隔太大的情况,绘制的图形也更加准确。
# 准确画出图像
X_plot = np.linspace(-3, 3, 100).reshape(100, 1) # 通过linspace在(-3,3)直接均匀取值100个,然后通过reshape变成一个二维矩阵
y_plot = poly100_reg.predict(X_plot)
# 现在绘制的图形会更加准确,因为x的取值是在(-3,3)均匀取值的,所以不会出现两个点之间相隔太大的情况
plt.scatter(x, y)
plt.plot(X_plot[:, 0], y_plot, color='r')
plt.show()
plt.axis([-3, 3, -1, 10])
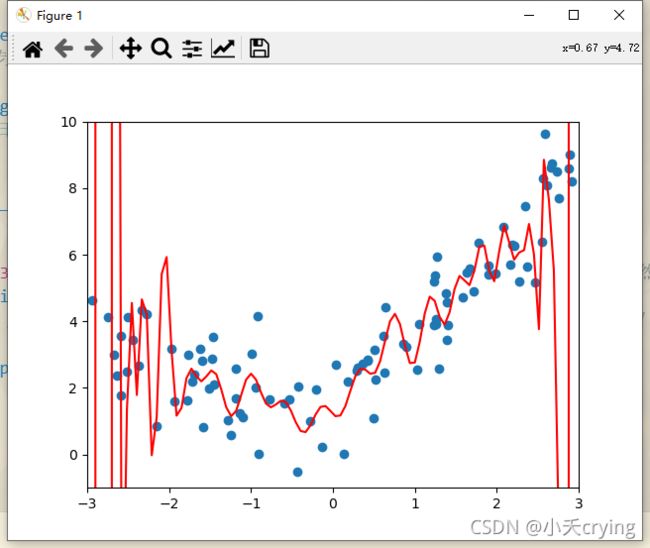
这就是真正的将degree=100后,多项式回归拟合的结果。
小总结:很显然这里的degree传入的值越高,最后我们的结果拟合的越好,我们一共有这么多样本点,其实我们总能找到一根曲线,将我们所有的样本点进行拟合(让所有的样本点落在这条曲线上,使我们的均方误差为0,这时的degree一定非常高)。这个拟合结果虽然从均方误差的角度看是非常好的,均方误差是更小的,但是这真的能更好反映样本数值走势的曲线吗,举个例子
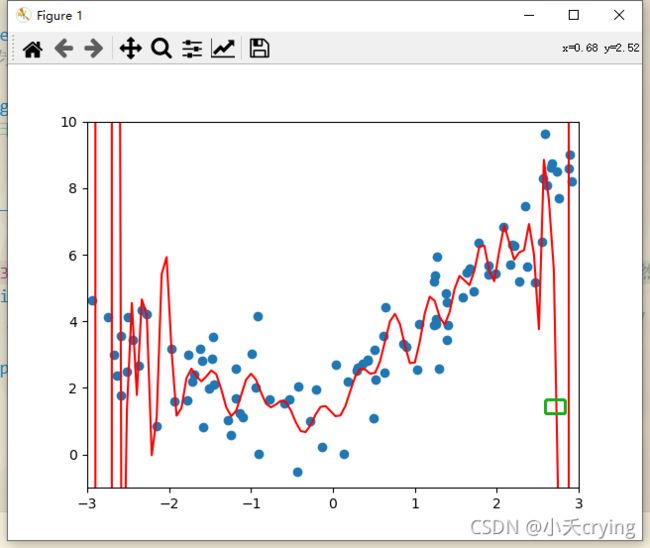
如果有个样本点x取值在2.8附近,曲线对应的y值就对应在我标出的绿色框的地方,但是我们的样本真正的形态不会出现在这里。
我们用了非常高维的数据,虽然使所有点对应拟合曲线,其均方误差更小,但是这根曲线已经不是我们想要的样子了,它为了拟合我们给出的所有样本点,变得太过复杂了,这种情况就叫做过拟合(overfitting)
2、欠拟合
其实在这片博客的一开始,我们直接用一条直线来拟合了我们的样本点,其实这种方式也并没有很好的反映原始数据的样本特征。但是他犯的错误不是太过复杂,而是太过简单了,这种情况称之为欠拟合(underfitting)

总结
通过多项式回归的方式可以非常直观的解释欠拟合与过拟合,就这篇博客的情况,我们原本的数据,如果通过二次方程生成的话,通过一次方程生成的结果就是欠拟合,我们使用高于二次方程得到的拟合结果,则对应过拟合。