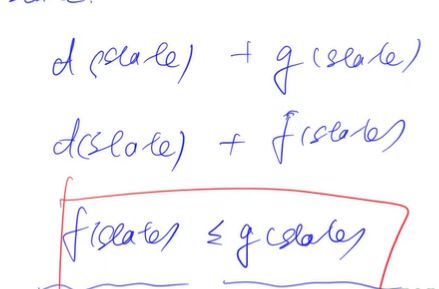1，莫队算法学习：eg1：小b的询问；2，A*算法：eg1：第k短路；eg2：八数码；
1，莫队算法：
可以解决大部分区间离线问题的离线算法；
主要思想是分块，时间复杂度：
；
具体实现：
所以这样挪区间，就可以得到所有区间的询问的答案；
但是还要处理：
分块的方法就是分成n的开方的大小；在对所有询问排序：
分块：
bool cmp(ji a,ji b)
{
return pos[a.l]==pos[b.l]?a.r
之后处理每个询问，然后用ans[]来记录每个询问的答案；
int l=1,r=0;
rep1(i,0,m)
{
while(q[i.l]r)add(++r);
while(q[i.l]>l)sub(l--);
while(q[i.r]
不同的题的add，和sub函数实现求值不同，框架一样的；
eg1：小b的询问；
题意：
莫队的模板题，看下代码吧：
#include
#pragma GCC optimize(2)
#define rep1(i,a,n) for(ll i=a;ia;i--)
#define per2(i,n,a) for(ll i=n;i>=a;i--)
#define quick_cin() cin.tie(0),cout.tie(0),ios::sync_with_stdio(false)
#define memset(a,i) memset((a),(i),sizeof (a))
#define memcpy(a,i) memcpy((a),(i),sizeof (a))
#define pb push_back
#define endl "\n"
#define lowbit(m) (-m&m)
#define yes cout<<"YES\n"
#define no cout<<"NO\n"
#define yi first
#define er second
using namespace std;
typedef long long ll;
typedef pair PII;
typedef double db;
const int N=5e4+10;
int n,m,k;
int pos[N];
int cnt[N];
struct ji
{
int l,r,xh;
}q[N];
bool cmp(ji a,ji b)
{
return pos[a.l]==pos[b.l]?a.r>n>>m>>k;
int siz=sqrt(n);
rep2(i,1,n)
{
cin>>a[i];
pos[i]=i/siz;
}
rep2(i,1,m)
{
cin>>q[i].l>>q[i].r;
q[i].xh=i;
}
sort(q+1,q+m+1,cmp);
int l=1,r=0;
rep2(i,1,m)
{
while(q[i].lr)add(++r);
while(q[i].l>l)sub(l++);
while(q[i].r
2，A*算法；
bfs的一种优化；
①：将队列换成优先队列（小根堆）；
②：按照从起点到当前点的真实距离+从当前点到终点的估计距离排序；
当终点第一次出队时，即可得到答案；
核心点是估价函数（启发函数），给每个点一个估价，然后按排序入队；按照我们认为最优的点去扩展；
核心条件：
当前状态为state,起点到state 的真实距离为d(state)，当前state到终点的真实距离为 g(state)；
当前state到终点的估计距离为f(state)；
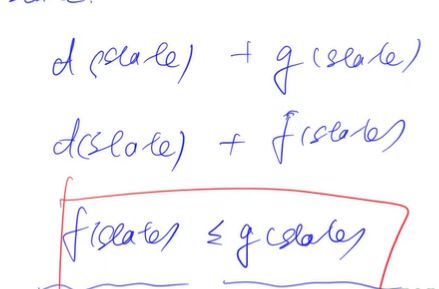
需要满足f(state)<=g(state)即可保证终点第一次出队时，就是最短距离；
注意事项：
①适用场景：一定有解的求解到最终状态的最短距离，如果无解的话，不如普通的bfs（）；
②：只能保证起点到终点的距离最小，不能保证中间状态到终点的距离最小；
eg1：第k短路；
本题中的评估距离可以用各个点到终点的距离，所以可以反向建图，再dijkstra求各个点到终点的距离；
然后就是A*的板子；
注释①：S==T就要求第k+1大；
注释②：在A*算法里，将其它点拓展进来时需要特判cnt[j]
#include
#pragma GCC optimize(2)
#define rep1(i,a,n) for(register ll i=a;ia;i--)
#define per2(i,n,a) for(register ll i=n;i>=a;i--)
#define quick_cin() cin.tie(0),cout.tie(0),ios::sync_with_stdio(false)
#define memset(a,i) memset((a),(i),sizeof (a))
#define memcpy(a,i) memcpy((a),(i),sizeof (a))
#define pro_q priority_queue
#define pb push_back
#define pf push_front
#define endl "\n"
#define lowbit(m) (-m&m)
#define yes cout<<"YES\n"
#define no cout<<"NO\n"
#define yi first
#define er second
using namespace std;
typedef pair PII;
typedef pair PIII;
typedef long long ll;
typedef double dob;
const int N=1e3+10,M=2e5+10;
int n,m,S,T,K;
int e[M],w[M],h[N],rh[N],ne[M],idx;
int dist[N],cnt[N];
int st[N];
void add(int h[],int a,int b,int c)
{
w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dijkstra()
{
pro_q,greater>q;
q.push({0,T});
memset(dist,0x3f);
dist[T]=0;
while(q.size())
{
auto t=q.top();
q.pop();
int ver=t.er;
if(st[ver])continue;
for(int i=rh[ver];~i;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[ver]+w[i])
{
dist[j]=dist[ver]+w[i];
q.push({dist[j],j});
}
}
}
}
int astar()
{
pro_q,greater>q;
q.push({dist[S],{0,S}});
//piii所存的含义为：评估值(真实值+评估值)，真实距离，该点编号
while(q.size())
{
auto t=q.top();
q.pop();
int ver=t.er.er,distance=t.er.yi;
cnt[ver]++;
if(cnt[T]==K)return distance;
for(int i=h[ver];~i;i=ne[i])
{
int j=e[i];
if(cnt[j]>n>>m;
rep2(i,1,m)
{
int a,b,c;
cin>>a>>b>>c;
add(h,a,b,c);
add(rh,b,a,c);
}
cin>>S>>T>>K;
if(S==T)K++;
dijkstra();
cout<
eg2：八数码；
评估距离还是人为推导数学严格推出来的，用到了曼哈顿距离；（所以本质上就是知道答案的方向了，给个启发函数判断下，往最优解（答案）搜？）
小细节挺多的，包括：偏移量要和操作字母的顺序对应，坐标转化，输出操作序列等；
#include
#pragma GCC optimize(2)
#define rep1(i,a,n) for(register ll i=a;ia;i--)
#define per2(i,n,a) for(register ll i=n;i>=a;i--)
#define quick_cin() cin.tie(0),cout.tie(0),ios::sync_with_stdio(false)
#define memset(a,i) memset((a),(i),sizeof (a))
#define memcpy(a,i) memcpy((a),(i),sizeof (a))
#define pro_q priority_queue
#define pb push_back
#define pf push_front
#define endl "\n"
#define lowbit(m) (-m&m)
#define yes cout<<"YES\n"
#define no cout<<"NO\n"
#define yi first
#define er second
using namespace std;
typedef pair PII;
typedef pair PIII;
typedef long long ll;
typedef double dob;
int f(string state)
{
int res=0;
rep1(i,0,state.size())
{
if(state[i]!='x')
{
int t=state[i]-'1';
res+=abs(i/3-t/3)+abs(i%3-t%3);
}
}
return res;
}
string bfs(string statrt)
{
int dx[]={-1,0,1,0},dy[]={0,1,0,-1};
char op[]={'u','r','d','l'};
string end="12345678x";
unordered_mapdist;
unordered_map>prev;
pro_q,vector>,greater>>q;
q.push({f(statrt),statrt});
dist[statrt]=0;
while(q.size())
{
auto t=q.top();q.pop();
string state=t.er;
if(state==end)break;
int step=dist[state];
int x,y;
rep1(i,0,state.size())
{
if(state[i]=='x')
{
x=i/3,y=i%3;
break;
}
}
string source=state;
rep1(i,0,4)
{
int a=x+dx[i],b=y+dy[i];
if(a>-1&&a<3&&b>-1&&b<3)
{
swap(state[x*3+y],state[a*3+b]);
if(!dist[state]||dist[state]>step+1)
{
dist[state]=step+1;
prev[state]={source,op[i]};
q.push({dist[state]+f(state),state});
}
swap(state[x*3+y],state[a*3+b]);
}
}
}
string res;
while(end!=statrt)
{
res+=prev[end].er;
end=prev[end].yi;
}
reverse(res.begin(),res.end());
return res;
}
signed main()
{
quick_cin();
string g,c,seq;
while(cin>>c)
{
g+=c;
if(c!="x")seq+=c;
}
int t=0;
rep1(i,0,seq.size())
rep1(j,i+1,seq.size())
if(seq[i]>seq[j])t++;
if(t&1)cout<<"unsolvable";
else cout<
