江南大学《机器学习》大作业-人脸图像性别分类-大报告
Jupyter Notebook实现见:https://blog.csdn.net/jty123456/article/details/109666045
代码开源库见:https://github.com/0Kirby/GenderRecognition
kaggle比赛地址:https://www.kaggle.com/c/jiangnan2020

![]()
绪 论
实验目的
《机器学习》是计算机类硕士生阶段的重要应用基础课程,旨在使学生了解机器学习的研究对象、研究内容、研究方法(包括理论基础和实验方法),和近年来的主要发展技术路线。本课程非学位课,为了培养学生以机器学习理论为基础从事相关应用研究的能力,学生的考核以大作业的形式进行。
通过看——查阅资料、做——复现已有资料的实验或做一个机器学习应用课题、写——将自己的研究工作写成技术报告,完成整个大作业。
实验要求
查阅资料
通过查阅资料,了解机器学习领域的新进展、新应用,结合课堂教学和教材的内容,根据指定课题,应用某一种或某几种算法解决问题,并分析实验结果。
完成实验
对于自己选定的研究内容,理解相关的算法原理和关键技术,并以实验加以验证和实现。要给出实验的程序和运行结果,程序语言采用Python。最后提交的程序要能够演示运行。
撰写技术报告
将所做工作的方法、原理、实验设计、所得结果及其比较分析等写成技术报告,并附上主要参考文献,说明程序的运行环境和运行方法。
进行演示
学生每人一组,单独完成大作业。提交大作业时进行现场演示,并进行提问交流。
实验内容
实验简介
本次实验名称为“人脸图像性别分类”,要求针对提供的人脸数据集,预测人脸性别。
本次大作业将提供 20000 多张已经分割的人脸图像,数据集的年龄从1岁覆盖到100多岁,包括了白种人、黄种人、黑种人等多种种族数据。数据集存在人脸姿态、光照、年龄等多种干扰,具有一定的挑战性。
本次比赛系机器学习课程2020级内部大作业,旨在通过相对简单的人脸性别识别二分类问题,完整地完成比赛过程。通过本次比赛,学生应该掌握数据集预处理的基本方法以及建模分析的方法等。设计者可以采用任何分类算法及数据预处理方法。下图1-1为实验界面。

数据集简介
数据集包括2万多张已经分割后的人脸图像。其中18000张作为训练集,其余作为测试集。人脸图像包括了从1岁到100多岁、各个肤色种族的数据,数据样本丰富。要求根据人脸图像,设计机器学习模型,自动判断性别。
- train.csv - 训练集,其中包括两列,第一列id是人脸图像的编号,即对应的文件名,第二列label是性别标签,0表示男性,1表示女性,如图1-2所示;
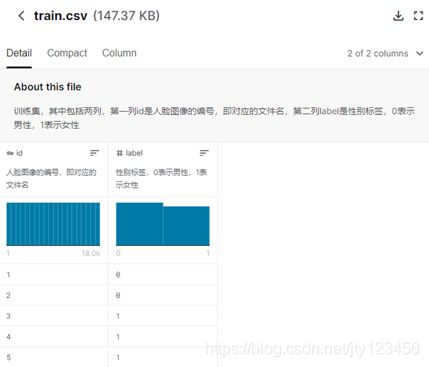
- test.csv - 测试集,只包括一列id,即测试集中所有的人脸图像的编号。测试集中没有性别标签,如图1-3所示;
- train文件夹 - 所有的训练图像,扩展名为jpg,其命名与train.csv中的id命名一致,如图1-4所示;
- test文件夹 - 所有的测试图像,扩展名为jpg,其命名与test.csv中的id命名一致,如图1-5所示;
- sampleSubmit.csv - 提交文件的样本,其中包括两列,第一列id是所有测试集的人脸图像的编号,即对应的文件名,第二列label是模型输出的性别标签,0表示男性,1表示女性,如图1-6所示;
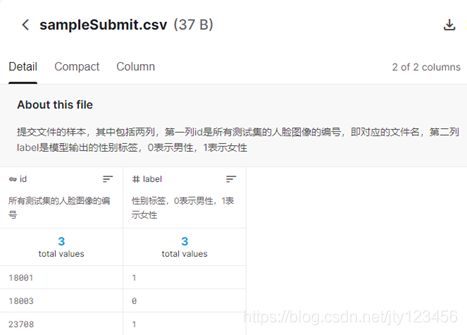
数据说明:id - 图像文件名,其对应图像为id.jpg;label - 图像标签,0 表示男性,1表示女性。
运行环境
硬件配置
| 名称 | 型号 | 备注 |
|---|---|---|
| CPU | Intel i7-10750H | 6核心12线程,基频2.60GHz |
| 内存 | Samsung 8GB | 3200MHz,DDR4 |
| 硬盘 | LITEON | 512GB,SSD |
| 显卡 | NVIDIA RTX 2060 | CUDA核心数1920,显存6GB |
软件环境
| 名称 | 版本 | 备注 |
|---|---|---|
| Windows | 10 | 20H2(10942.572) |
| Python | 3.8.6 | |
| Pycharm | 2020.2.3 | Professional |
| NVIDIA GPU驱动 | 442.23 | |
| CUDA工具包 | 10.1 | |
| CUPTI | CUDA工具包附带 | |
| cuDNN | 7.6.0 | for CUDA 10.1 |
| TensorRT | 6.0 |
第三方PyPI包
| 名称 | 版本 | 备注 |
|---|---|---|
| Tensorflow | 2.3.1 | 深度学习框架 |
| Keras | 2.4.3 | 基于Tensorflow的实现 |
| scikit-learn | 0.23.2 | 机器学习库 |
| matplotlib | 3.3.2 | 绘图库 |
| pandas | 1.1.3 | 数据处理库 |
| numpy | 1.19.2 | 矩阵库 |
| opencv-Python | 4.4.0.44 | 图像处理库 |
算法原理与分析
全连接神经网络
简介
全连接神经网络(Fully connected neural network)是一种具有三层或三层以上的多层神经网络,每一层都由若干个神经元组成,它的左右各层之间的各个神经元实现了全连接。也就是说,左层的每一个神经元与右层的每个神经元都有连接,而上下层的各神经元之间没有连接。
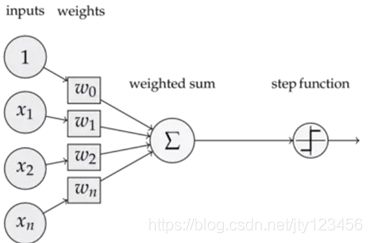
下图2-1为单层计算单元(神经元)的神经网络,也叫做感知器。感知器由一个线性组合器和一个二值阈值元件组成,实际上是一种二元线性分类器。它将输入和权重做乘积并求和,如果是分类问题,则最后再经过一个阶跃函数,输出二值0或1。
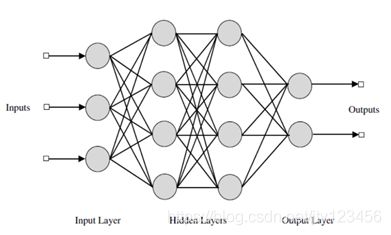
上图2-2是一个全连接神经网络的结构,整个网络由三个部分组成:输入层、隐藏层和输出层。其中输入层由三个神经元组成的,表示整个网络的输入是一个1 × \times × 3的矩阵;隐藏层是两层四个神经元相连构成的,它接收从上一层(即输入层)传来的输入信息,并对信息进行对应的运算;输出层是由两个神经元组成的,表示输出结果是一个1 × \times × 2的矩阵,如[1,0]表示正样本,[0,1]表示负样本。
BP反向传播
全连接神经网络按监督学习方式进行训练,当一对学习模式提供给网络后,其神经元的激活值将从输入层经过各隐藏层向输出层传播,在输出层的各神经元输出对应于输入模式的网络响应,然后按减少希望输出与实际输出误差的原则,从输出层经各隐藏层最后回到输入层,逐层修正各连接权值。
由于这种修正过程是从输入层到输入层逐层进行的,所以称之为“误差反向传播”(Back propagation)。随着这种误差反向传播训练的不断进行,网络对输入模式响应的正确率也将不断提高。正因为全连接神经网络有处于中间位置的隐藏层,并有相应的学习规则可循,因此可训练这种网络,使其具有对非线性模式的识别能力。
激活函数
激活函数(Activation function),就是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。正如我们刚才在2.1.1节中看过的感知器,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合。
激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。在本次实验中,主要使用了以下两种激活函数:
-
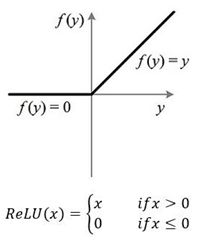
ReLu:线性整流函数(Rectified linear unit),又称修正线性单元,用于隐藏层神经元的输出。函数图像及定义如下图2-3所示:
-
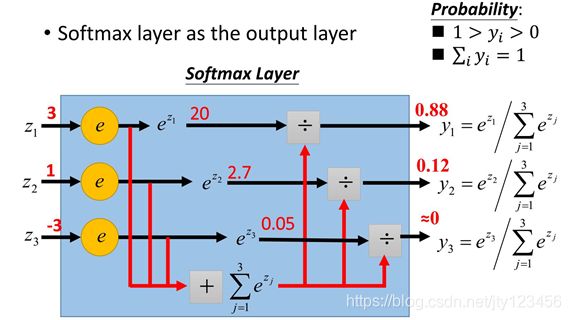
Softmax:用于神经网络最后的输出层中,将各输出的预测分量归一化为概率的形式。如下图2-4中所示,输出分量 z i z_i zi= [3,1,-3],首先计算他们以e为底数的 z i z_i zi次幂,然后令 y i y_i yi为刚才的计算结果占结果之和的比重,从而将输出值转化为属于各分类的概率为 z i ~ \widetilde{z_i} zi =[0.88,0.12,0]。
卷积神经网络
简介
为什么全连接神经网络在训练后能够对图像进行分类?那肯定是因为它学到了东西,学到了图片中的某些空间结构,不同性别的人脸的空间结构肯定是不一样的,而这样的空间结构就是由像素点与像素点之间的关系形成。我们再仔细看全连接神经网络的输入层和第一个隐藏层,发现它对输入的所有像素点都是同等对待的,也就是说它此时并没有考虑像素点与像素点之间的关系。然而一张照片所显示出的画面是连续的,因此一个像素点和周围的像素点存在着某种关联。如果我们能利用好这个特性,便能够提高识别的精度。
卷积神经网络(Convolutional Neural Network)正是为了解决这个问题而被提出的。
局部感受野
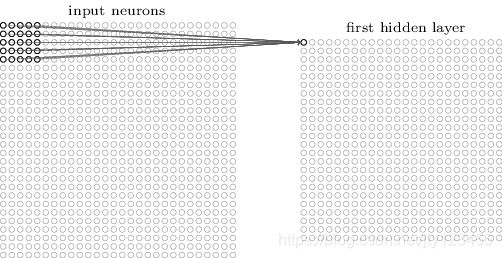
在全连接神经网络中,我们会把输入层的每个神经元都与第一个隐藏层的每个神经元连接。而在卷积神经网络中,第一个隐藏层的神经元只与局部区域输入层的神经元相连。下图2-5 中,输入为28 × \times × 28的矩阵,表示了第一个隐藏层的第一个神经元与局部区域输入层的前5 × \times × 5共25个神经元相连的情况,如图2-5所示。这个5 × \times × 5对应着Conv2D中的kernel_size参数,即窗口大小。
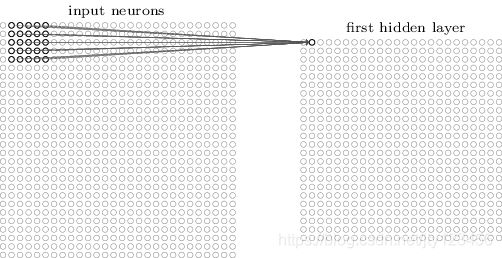
我们将输入层中的神经元均向右滑动一个单位,便得到了一个新的5 × \times × 5的神经元。与之对应,第一个隐藏层中的神经元也向右滑动一个单位,便得到了从输入层新的5 × \times × 5神经元映射出的隐藏层中第二个神经元,如下图2-6所示。
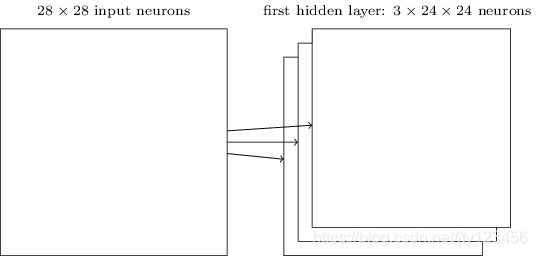
以此类推通过不断滑动窗口,可以形成第一个隐藏层。由于我们的输入矩阵是28 × \times × 28,窗口是5 × \times × 5,因此可以得到一个24 × \times × 24(28-5+1)个神经元的隐藏层
这里我们的窗口只滑动了一个像素,对应着Conv2D中的Stride参数。我们也可以滑动多步,在训练时可以根据效果调整。
权值共享
第一个隐藏层的中的每个神经元有5 × \times × 5个权值参数与之对应。而隐藏层的这24 × \times × 24个神经元它们的权值和偏移值是共享的,可以用以下公式来表示:
a 1 = σ ( b + w ∗ a 0 ) a^1=\sigma(b+w\ast a^0) a1=σ(b+w∗a0)
其中a1表示隐藏层的输出,a0表示隐藏层的输入,∗表示卷积操作。由于权值共享,窗口移来移去还是同一个窗口,也就意味着第一个隐藏层所有的神经元从输入层探测到的是同一种特征,只是从输入层的不同位置探测到(图片的中间,左上角,右下角等等)。我们想要学习更多的特征,就需要更多的窗口。如果用三个窗口的话如下图2-7所示:
池化
池化层通常接在卷积层后面,使用它的目的就是为了简化卷积层的输出。通俗地理解,池化层也是在卷积层上架了一个窗口,但这个窗口比卷积层的窗口简单了许多,不需要权重和偏置等参数,只是对窗口范围内的神经元做简单的操作,如求最大值(Max-pooling),最后把求得的值作为池化层神经元的输入值。如下图2-8所示,这是一个2 × \times × 2的窗口,它将隐藏层中每2 × \times × 2个神经元映射为最大池化层中的一个神经元作为输出,如下图2-8所示。
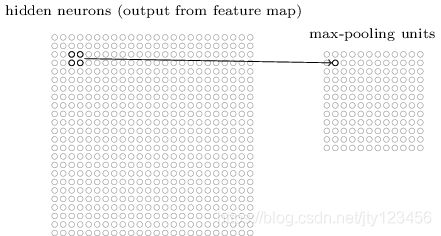
由于经过了卷积操作,模型从输入层学到的特征反映在卷积层上。所以最大池化层做的事就是去检测这个特征是否在窗口覆盖范围的区域内。经过池化后,如我们刚才使用的2 × \times × 2窗口,将24 × \times × 24的卷积输出压缩成12 × \times × 12的矩阵,大大减少了我们学到的特征值,也就大大减少了后面网络层的参数。
输出
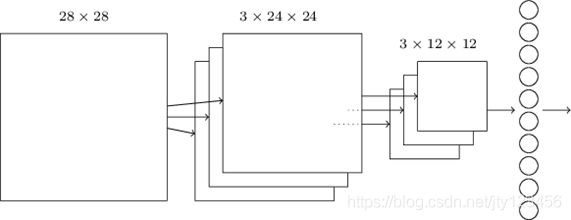
和全连接神经网络一样,将最后的12 × \times × 12矩阵展平成144个神经元的一维向量,再加上输出层即可得到整个卷积神经网络的完整结构,如图2-9所示。
实验设计
数据预处理
以文件名通过循环的方式,分别读取train和test文件夹中的每张图片。使用opencv库的imread传入图片的完整路径,并加上cv2.IMREAD_GRAYSCALE参数以灰度图的形式读取。为了控制内存资源的消耗,这里我们把读入图片的尺寸从200 × \times × 200压缩到100 × \times × 100。最后把所有图片都放在一起,如训练集的所有图片将会形成一个(100,100,18000)的numpy数组。
然后对表示图片的矩阵进行归一化处理,即除以255.0转化为0~1之间的值。最后将每张图片存入list,并转化为numpy数组,将训练集和测试集图片保存为train_images和test_images。下图3-1是一张已经归一化并灰度化的图片。

使用pandas库中的read_csv方法读取包含训练集标签的train.csv,从数据帧中提取实际的值。再取出其中的第一列,即只包含0,1标签而不包括id的数据。
由于卷积需要4个维度的矩阵,刚才是以灰度的方式读取图片,丢失了通道的信息,因此我们需要丢失了通道的信息,因此我们需要通过reshape方法扩充一维,即每张图片的shape从(100,100)扩充到(100,100,1)。
我们在进行模型拟合时,因为会发生震荡,所以每一轮并不一定都能降低误差和提高精度。为了实时评估训练的结果,我们可以取出训练集中的一部分图片作为验证集,在每一轮训练结束后使用该轮得到的模型对验证集中的图片进行预测,并反馈验证集精度。
在这里我们使用sklearn库中的model_selection类中的train_test_split方法,对train文件夹18000张图片进行训练集和测试集的划分。通过四个变量X_train, X_val, Y_train, Y_val分别保存训练集图片、验证集图片、训练集标签,验证集标签。指定test_size为0.1,也即取出18000张图片中10%图片作为验证集,剩余的90%图片作为新的训练集,与之对应的标签也进行同样的划分。最后还要设定random_state为一固定值3,以便我们每次运行都是取出相同的图片进行训练和验证。
数据增强
当我们的数据集不足、分类数过多、数据特征过于复杂时,我们往往需要使用数据增强。数据增强是根据已有的数据进行一些变换,生成一些新的图片加入到原先的训练集中,可以扩充我们的训练集,从而达到更好的训练效果。在本次实验中,在优化的卷积模型中主要使用了以下5种数据增强的方式:
- 高斯噪声:在图片中加入均方差为0.1的高斯噪声;
- 随机翻转:将图片随机进行水平翻转(镜像对称);
- 随机偏移:将图片随机斜向偏移10%(如把正方形变形成平行四边形);
- 随机旋转:将图片随机旋转10%(向左或向右旋转36°);
- 随机缩放:将图片随机放大或缩小10%。
下图3-2中是一张图片经过数据增强后得到的图片。
模型设计
在本次实验中,我对模型的选择和设计经过了很多次尝试。在对这些尝试进行总结后,大体可分为三个部分:全连接模型、卷积模型和优化的卷积模型。所有模型均使用深度学习框架Tensorflow中的Keras库作为后端,采用sequential顺序结构,按照插入各层的顺序进行模型的构建。
其中Dense是全连接层,所有神经元都是相连的,参数units表示神经元个数,input_shape表示输入矩阵的大小;Flatten是展平层,将多维的输入矩阵压成一行;Conv_2D是二维卷积层,在该层中进行卷积操作,参数kernel_size表示卷积核的大小,strides表示每次移动窗口的步数,padding表示是否将矩阵压小;BatchNormalization是批次标准化层,通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布;MaxPooling2D是二维最大池化层,可以简化卷积层输出的结果,将其压缩;Dropout层将一部分神经元随机失活,降低了过拟合的可能性,参数rate表示失活的神经元占总神经元个数的比例。
全连接模型
最先采用的模型是最简单的全连接神经网络,一共包含3层:输入层、隐藏层和输出层。输入层的大小是200 × \times × 200,以原始像素来接收每张图片;然后通过一个展平层,把200 × \times × 200展平成40000 × \times × 1;再将这40000个特征输入到隐藏层中去,其中隐藏层包含512个神经元,最后通过输出层输出;由于是二分类问题,输出层共有2个神经元,用softmax函数优化,其余层用ReLu函数优化。模型如下图3-3所示。
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) (None, 40000) 0
_________________________________________________________________
dense (Dense) (None, 512) 20480512
_________________________________________________________________
dense_1 (Dense) (None, 2) 1026
=================================================================
Total params: 20,481,538
Trainable params: 20,481,538
Non-trainable params: 0
_________________________________________________________________
卷积模型
由于全连接神经网络的能力有限,考虑更换成了卷积神经网络。为了加快训练速度,将输入图片的像素压缩成了28 × \times × 28。刚开始尝试的时候用的是两层卷积,第一个卷积层的神经元的个数为32,卷积核大小为3 × \times × 3;然后接着一个最大池化层,池化大小为2 × \times × 2,步数为2;第二个卷积层的神经元个数扩充了一倍为64,卷积核大小不变;再接一个同样的最大池化层,然后添加一个展平层将7 × \times × 7 × \times × 64的输入展平成3136 × \times × 1;与第二个卷积层连接的是一个包含128个神经元的隐藏层,加上一个使20%神经元失活的Dropout层;在整个模型的最后,仍然加上有两个神经元的输出层,用softmax函数优化,而卷积层均用ReLu函数优化。模型如下图3-4所示。
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 28, 28, 32) 320
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 14, 14, 32) 0
_________________________________________________________________
conv2d_1 (Conv2D) (None, 14, 14, 64) 18496
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 7, 7, 64) 0
_________________________________________________________________
flatten (Flatten) (None, 3136) 0
_________________________________________________________________
dense (Dense) (None, 128) 401536
_________________________________________________________________
dropout (Dropout) (None, 128) 0
_________________________________________________________________
dense_1 (Dense) (None, 2) 258
=================================================================
Total params: 420,610
Trainable params: 420,610
Non-trainable params: 0
_________________________________________________________________
优化的卷积模型
从卷积模型中看到了训练效果的提升,因此基于原本的卷积模型进行了修改。为了尽可能减少图片信息的丢失,将压缩图片的像素28 × \times × 28扩充到100 × \times × 100。为了让CNN能学到更多的东西,不以灰度读取图片,而以正常的RGB三通道方式读取。因此输入矩阵的大小为(100,100,3),然后输入到3.2节中增加的数据增强层中,这一层也被视为是一个顺序模型。如下图3-5所示。
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
gaussian_noise (GaussianNois (None, 100, 100, 3) 0
_________________________________________________________________
random_flip (RandomFlip) (None, 100, 100, 3) 0
_________________________________________________________________
random_translation (RandomTr (None, 100, 100, 3) 0
_________________________________________________________________
random_rotation (RandomRotat (None, 100, 100, 3) 0
_________________________________________________________________
random_zoom (RandomZoom) (None, 100, 100, 3) 0
=================================================================
Total params: 0
Trainable params: 0
Non-trainable params: 0
_________________________________________________________________
然后我们再看模型的主体部分,首先是两个的相连的卷积层,神经元分别为25和50,卷积核大小均为3 × \times × 3;再加上批次标准化层、最大池化层和失活率为0.2的Dropout层;以同样的方式再添加两遍和上述相同的层,只不过卷积层的神经元个数分别为50、100、100和200;完成所有的卷积操作后,便来到了展平层,将最后一个卷积层的输出12 × \times × 12 × \times × 200展平成28800 × \times × 1;随后我们添加3个全连接层,神经元个数分别为50、100和200,并在它们之间插入批次标准化层和失活率为0.2的Dropout层;最后的输出层不变仍为两个神经元,用softmax函数优化,而卷积层均用ReLu函数优化。整个模型如下图3-6所示。
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
sequential (Sequential) (None, 100, 100, 3) 0
_________________________________________________________________
conv2d (Conv2D) (None, 100, 100, 25) 700
_________________________________________________________________
conv2d_1 (Conv2D) (None, 100, 100, 50) 11300
_________________________________________________________________
batch_normalization (BatchNo (None, 100, 100, 50) 200
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 50, 50, 50) 0
_________________________________________________________________
dropout (Dropout) (None, 50, 50, 50) 0
_________________________________________________________________
conv2d_2 (Conv2D) (None, 50, 50, 50) 22550
_________________________________________________________________
conv2d_3 (Conv2D) (None, 50, 50, 100) 45100
_________________________________________________________________
batch_normalization_1 (Batch (None, 50, 50, 100) 400
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 25, 25, 100) 0
_________________________________________________________________
dropout_1 (Dropout) (None, 25, 25, 100) 0
_________________________________________________________________
conv2d_4 (Conv2D) (None, 25, 25, 100) 90100
_________________________________________________________________
conv2d_5 (Conv2D) (None, 25, 25, 200) 180200
_________________________________________________________________
batch_normalization_2 (Batch (None, 25, 25, 200) 800
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 12, 12, 200) 0
_________________________________________________________________
dropout_2 (Dropout) (None, 12, 12, 200) 0
_________________________________________________________________
flatten (Flatten) (None, 28800) 0
_________________________________________________________________
dense (Dense) (None, 50) 1440050
_________________________________________________________________
batch_normalization_3 (Batch (None, 50) 200
_________________________________________________________________
dropout_3 (Dropout) (None, 50) 0
_________________________________________________________________
dense_1 (Dense) (None, 100) 5100
_________________________________________________________________
batch_normalization_4 (Batch (None, 100) 400
_________________________________________________________________
dense_2 (Dense) (None, 200) 20200
_________________________________________________________________
batch_normalization_5 (Batch (None, 200) 800
_________________________________________________________________
dropout_4 (Dropout) (None, 200) 0
_________________________________________________________________
dense_3 (Dense) (None, 2) 402
=================================================================
Total params: 1,818,502
Trainable params: 1,817,102
Non-trainable params: 1,400
_________________________________________________________________
模型训练和输出
在完成对模型的构建和编译后,可以使用model.fit函数对模型进行训练了。除了训练轮数不同以外,训练均采用默认参数。其中全连接模型训练轮数为20,卷积模型为30,而优化的卷积模型为1000。
我们可以在训练过程中添加callbacks,让Keras以最优的val_accuracy(验证集精度)来保存当前训练的权重,这样可以在训练的震荡中取到局部最优的模型。还可以记录模型训练中的信息,如训练集误差、训练集精度、验证集误差、验证集精度,并在训练完毕后绘制出图像。
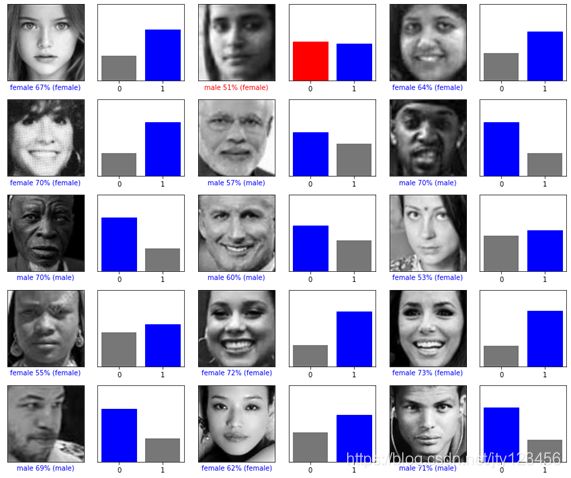
在得到训练好的模型之后,我们调用model.predict函数,其中传入测试图片,对测试集进行预测。由于输出层采用了softmax函数进行优化,因此输出的是和为1的两个概率值,如[99.9999,0.0001]。为了更直观地显示输出结果,我们把它对应到样例输出sampleSubmit.csv中要求的0和1。最后根据test.csv中的id值把最终的预测结果写入submission.csv,即完成了整个实验。下图3-7展示了其中15张图片的预测结果,0表示男性的概率,1表示女性的概率,其中有一张图片预测错误。
实验结果与分析
全连接模型
由于全连接模型比较简单,因此训练和收敛都很快。每轮训练需要4s的时间,经过20轮的训练后,训练集的精度从开始的0.6993提升到0.8453。训练过程如下图4-1所示。
Epoch 1/20
450/450 [==============================] - 4s 9ms/step - loss: 2.2211 - accuracy: 0.6993
Epoch 2/20
450/450 [==============================] - 4s 9ms/step - loss: 0.6702 - accuracy: 0.7818
Epoch 3/20
450/450 [==============================] - 4s 9ms/step - loss: 0.4844 - accuracy: 0.7994
Epoch 4/20
450/450 [==============================] - 4s 9ms/step - loss: 0.4280 - accuracy: 0.8117
Epoch 5/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3961 - accuracy: 0.8209
Epoch 6/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3925 - accuracy: 0.8212
Epoch 7/20
450/450 [==============================] - 4s 9ms/step - loss: 0.4015 - accuracy: 0.8187
Epoch 8/20
450/450 [==============================] - 4s 9ms/step - loss: 0.4021 - accuracy: 0.8153
Epoch 9/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3818 - accuracy: 0.8269
Epoch 10/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3763 - accuracy: 0.8319
Epoch 11/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3887 - accuracy: 0.8228
Epoch 12/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3819 - accuracy: 0.8239
Epoch 13/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3805 - accuracy: 0.8264
Epoch 14/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3794 - accuracy: 0.8293
Epoch 15/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3651 - accuracy: 0.8368
Epoch 16/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3916 - accuracy: 0.8249
Epoch 17/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3718 - accuracy: 0.8322
Epoch 18/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3565 - accuracy: 0.8388
Epoch 19/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3544 - accuracy: 0.8444
Epoch 20/20
450/450 [==============================] - 4s 9ms/step - loss: 0.3459 - accuracy: 0.8453
训练好模型后,我们将含有测试集图片的数组传入predict函数进行预测,经过1秒后,可以看到测试精度为0.8486,于训练集精度相差无几。但是精度并不高,主要是因为全连接模型比较简单,能力有限,并不足以应对复杂的特征。下图4-2为全连接模型预测的结果。
113/113 - 1s - loss: 0.3401 - accuracy: 0.8486
Test accuracy: 0.8486111164093018
使用全连接模型对测试集进行预测,上传生成的csv文件到kaggle平台,得分为0.85599,如图4-3所示。

卷积模型
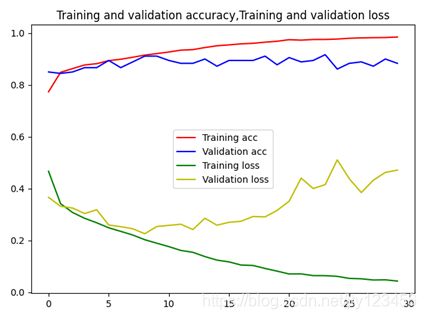
卷积模型和全连接模型相比,虽然增加了模型的层数,但是输入数据的大小从200 × \times × 200缩小到28 × \times × 28,故训练速度获得了显著提升,每轮从4s减少到1s。经过30轮训练后,验证集的精度在0.9000附近震荡。图4-4为卷积模型的训练结果,图4-5为卷积模型的精度、误差曲线。
Epoch 1/30
557/557 [==============================] - 1s 3ms/step - loss: 0.4667 - accuracy: 0.7734 - val_loss: 0.3662 - val_accuracy: 0.8500
Epoch 2/30
557/557 [==============================] - 1s 2ms/step - loss: 0.3417 - accuracy: 0.8488 - val_loss: 0.3316 - val_accuracy: 0.8444
Epoch 3/30
557/557 [==============================] - 1s 2ms/step - loss: 0.3076 - accuracy: 0.8630 - val_loss: 0.3248 - val_accuracy: 0.8500
Epoch 4/30
557/557 [==============================] - 1s 2ms/step - loss: 0.2853 - accuracy: 0.8770 - val_loss: 0.3036 - val_accuracy: 0.8667
Epoch 5/30
557/557 [==============================] - 1s 2ms/step - loss: 0.2680 - accuracy: 0.8820 - val_loss: 0.3182 - val_accuracy: 0.8667
Epoch 6/30
557/557 [==============================] - 1s 2ms/step - loss: 0.2487 - accuracy: 0.8937 - val_loss: 0.2596 - val_accuracy: 0.8944
Epoch 7/30
557/557 [==============================] - 1s 2ms/step - loss: 0.2348 - accuracy: 0.8990 - val_loss: 0.2529 - val_accuracy: 0.8667
Epoch 8/30
557/557 [==============================] - 1s 2ms/step - loss: 0.2207 - accuracy: 0.9068 - val_loss: 0.2449 - val_accuracy: 0.8889
Epoch 9/30
557/557 [==============================] - 1s 2ms/step - loss: 0.2026 - accuracy: 0.9152 - val_loss: 0.2257 - val_accuracy: 0.9111
Epoch 10/30
557/557 [==============================] - 1s 2ms/step - loss: 0.1891 - accuracy: 0.9210 - val_loss: 0.2536 - val_accuracy: 0.9111
Epoch 11/30
557/557 [==============================] - 1s 2ms/step - loss: 0.1759 - accuracy: 0.9271 - val_loss: 0.2580 - val_accuracy: 0.8944
Epoch 12/30
557/557 [==============================] - 1s 2ms/step - loss: 0.1612 - accuracy: 0.9342 - val_loss: 0.2624 - val_accuracy: 0.8833
Epoch 13/30
557/557 [==============================] - 1s 2ms/step - loss: 0.1540 - accuracy: 0.9363 - val_loss: 0.2419 - val_accuracy: 0.8833
Epoch 14/30
557/557 [==============================] - 1s 2ms/step - loss: 0.1375 - accuracy: 0.9443 - val_loss: 0.2854 - val_accuracy: 0.9000
Epoch 15/30
557/557 [==============================] - 1s 2ms/step - loss: 0.1239 - accuracy: 0.9511 - val_loss: 0.2586 - val_accuracy: 0.8722
Epoch 16/30
557/557 [==============================] - 1s 2ms/step - loss: 0.1171 - accuracy: 0.9545 - val_loss: 0.2698 - val_accuracy: 0.8944
Epoch 17/30
557/557 [==============================] - 1s 2ms/step - loss: 0.1049 - accuracy: 0.9585 - val_loss: 0.2737 - val_accuracy: 0.8944
Epoch 18/30
557/557 [==============================] - 1s 2ms/step - loss: 0.1031 - accuracy: 0.9606 - val_loss: 0.2921 - val_accuracy: 0.8944
Epoch 19/30
557/557 [==============================] - 1s 2ms/step - loss: 0.0917 - accuracy: 0.9649 - val_loss: 0.2908 - val_accuracy: 0.9111
Epoch 20/30
557/557 [==============================] - 1s 2ms/step - loss: 0.0813 - accuracy: 0.9686 - val_loss: 0.3158 - val_accuracy: 0.8778
Epoch 21/30
557/557 [==============================] - 1s 2ms/step - loss: 0.0704 - accuracy: 0.9746 - val_loss: 0.3511 - val_accuracy: 0.9056
Epoch 22/30
557/557 [==============================] - 1s 2ms/step - loss: 0.0705 - accuracy: 0.9728 - val_loss: 0.4405 - val_accuracy: 0.8889
Epoch 23/30
557/557 [==============================] - 1s 2ms/step - loss: 0.0642 - accuracy: 0.9754 - val_loss: 0.4002 - val_accuracy: 0.8944
Epoch 24/30
557/557 [==============================] - 1s 2ms/step - loss: 0.0639 - accuracy: 0.9755 - val_loss: 0.4153 - val_accuracy: 0.9167
Epoch 25/30
557/557 [==============================] - 1s 2ms/step - loss: 0.0612 - accuracy: 0.9770 - val_loss: 0.5109 - val_accuracy: 0.8611
Epoch 26/30
557/557 [==============================] - 1s 2ms/step - loss: 0.0533 - accuracy: 0.9800 - val_loss: 0.4379 - val_accuracy: 0.8833
Epoch 27/30
557/557 [==============================] - 1s 2ms/step - loss: 0.0518 - accuracy: 0.9815 - val_loss: 0.3845 - val_accuracy: 0.8889
Epoch 28/30
557/557 [==============================] - 1s 2ms/step - loss: 0.0471 - accuracy: 0.9824 - val_loss: 0.4323 - val_accuracy: 0.8722
Epoch 29/30
557/557 [==============================] - 1s 2ms/step - loss: 0.0478 - accuracy: 0.9829 - val_loss: 0.4624 - val_accuracy: 0.9000
Epoch 30/30
557/557 [==============================] - 1s 2ms/step - loss: 0.0430 - accuracy: 0.9849 - val_loss: 0.4711 - val_accuracy: 0.8833
使用卷积模型对测试集进行预测,上传生成的csv文件到kaggle平台,得分为0.90574,如图4-6所示。

优化的卷积模型
优化的卷积模型使用了更大的图片分辨率,从28 × \times × 28扩充到了100 × \times × 100。为了让模型学习到更多特征,使用RGB的方式读取图片。为了减少训练集部分图片特征不足的影响,使用了数据增强技术。
模型的训练分为两个部分。第一部分是取出训练集中10%的图片进行作为验证集来评估训练的结果,剩余90%作为实际的训练集。总训练轮数为300,并在训练中添加一些回调:
- ModelCheckpoint:使用val_accuracy(验证集精度)是否提升作为指标,一旦有提升则立刻保存当前训练的权重,从而能在所有训练轮数中保存与验证集最贴切的模型;
- ReduceLROnPlateau:使用val_loss(验证集误差)是否降低作为指标,如果在3个训练轮数后没有降低,则降低学习率0.0001,可以让模型更加容易接近局部最优减少震荡;
- EarlyStopping:使用val_loss(验证集误差)是否降低作为指标,如果在50个训练轮数后没有降低,则立即停止训练,从而避免因模型拟合而造成不必要的资源浪费。
经过300轮的训练后,训练集精度能达到0.9120,训练集精度最高能达到0.92611,并将此时的权重保存。图4-7为优化的卷积模型的300轮训练结果,图4-8为优化的卷积模型的300轮精度、误差曲线。
Epoch 297/300
32/32 [==============================] - ETA: 0s - loss: 0.3211 - accuracy: 0.9123
Epoch 00297: val_accuracy did not improve from 0.92611
32/32 [==============================] - 7s 231ms/step - loss: 0.3211 - accuracy: 0.9123 - val_loss: 0.3913 - val_accuracy: 0.9194
Epoch 298/300
32/32 [==============================] - ETA: 0s - loss: 0.3213 - accuracy: 0.9120
Epoch 00298: val_accuracy did not improve from 0.92611
32/32 [==============================] - 7s 231ms/step - loss: 0.3213 - accuracy: 0.9120 - val_loss: 0.3923 - val_accuracy: 0.9194
Epoch 299/300
32/32 [==============================] - ETA: 0s - loss: 0.3220 - accuracy: 0.9112
Epoch 00299: val_accuracy did not improve from 0.92611
32/32 [==============================] - 7s 231ms/step - loss: 0.3220 - accuracy: 0.9112 - val_loss: 0.3859 - val_accuracy: 0.9256
Epoch 300/300
32/32 [==============================] - ETA: 0s - loss: 0.3215 - accuracy: 0.9114
Epoch 00300: val_accuracy did not improve from 0.92611
32/32 [==============================] - 7s 238ms/step - loss: 0.3215 - accuracy: 0.9114 - val_loss: 0.3866 - val_accuracy: 0.9250
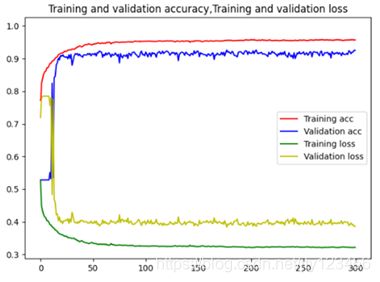
在确定好模型的参数后,进入第二部分的训练。第二部分的训练则是不划分训练集和验证集,把18000张图片都拿去训练。为了使模型尽量拟合,采用训练轮数为1000。移除上一部分的所有callback,防止没有达到1000轮的时候已经早停了,或者由于学习率下降到0导致训练停滞。在1000轮训练完后,使用model.save保存第1000轮时的权重,并绘制出训练集精度和误差的曲线。图4-9为优化的卷积模型的前25轮和后5轮的训练结果,图4-10为优化的卷积模型的1000轮精度、误差曲线(只含训练集)。
Epoch 1/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.5812 - accuracy: 0.7163
Epoch 2/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.5549 - accuracy: 0.7458
Epoch 3/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.5319 - accuracy: 0.7698
Epoch 4/1000
563/563 [==============================] - 8s 13ms/step - loss: 0.5177 - accuracy: 0.7853
Epoch 5/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.5033 - accuracy: 0.8017
Epoch 6/1000
563/563 [==============================] - 8s 14ms/step - loss: 0.5021 - accuracy: 0.8033
Epoch 7/1000
563/563 [==============================] - 8s 14ms/step - loss: 0.4940 - accuracy: 0.8094
Epoch 8/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.4870 - accuracy: 0.8168
Epoch 9/1000
563/563 [==============================] - 8s 14ms/step - loss: 0.4838 - accuracy: 0.8218
Epoch 10/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.4783 - accuracy: 0.8256
Epoch 11/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.4854 - accuracy: 0.8169
Epoch 12/1000
563/563 [==============================] - 8s 13ms/step - loss: 0.4759 - accuracy: 0.8304
Epoch 13/1000
563/563 [==============================] - 8s 14ms/step - loss: 0.4717 - accuracy: 0.8334
Epoch 14/1000
563/563 [==============================] - 8s 14ms/step - loss: 0.4669 - accuracy: 0.8386
Epoch 15/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.4671 - accuracy: 0.8382
Epoch 16/1000
563/563 [==============================] - 8s 14ms/step - loss: 0.4636 - accuracy: 0.8427
Epoch 17/1000
563/563 [==============================] - 8s 14ms/step - loss: 0.4629 - accuracy: 0.8435
Epoch 18/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.4678 - accuracy: 0.8374
Epoch 19/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.4619 - accuracy: 0.8434
Epoch 20/1000
563/563 [==============================] - 8s 14ms/step - loss: 0.4575 - accuracy: 0.8498
Epoch 21/1000
563/563 [==============================] - 8s 14ms/step - loss: 0.4619 - accuracy: 0.8437
Epoch 22/1000
563/563 [==============================] - 8s 14ms/step - loss: 0.4590 - accuracy: 0.8468
Epoch 23/1000
563/563 [==============================] - 8s 14ms/step - loss: 0.4567 - accuracy: 0.8487
Epoch 24/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.4526 - accuracy: 0.8539
Epoch 25/1000
563/563 [==============================] - 8s 14ms/step - loss: 0.4539 - accuracy: 0.8509
=========================================================================================
Epoch 996/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.3703 - accuracy: 0.9403
Epoch 997/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.3705 - accuracy: 0.9407
Epoch 998/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.3721 - accuracy: 0.9392
Epoch 999/1000
563/563 [==============================] - 8s 13ms/step - loss: 0.3702 - accuracy: 0.9408
Epoch 1000/1000
563/563 [==============================] - 7s 13ms/step - loss: 0.3679 - accuracy: 0.9437
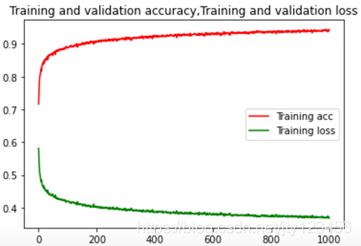
使用卷积模型对测试集进行预测,上传生成的csv文件到kaggle平台,得分为0.92782,如图4-11所示。

可以看到,从全连接模型到卷积模型,精度获得了显著提升,说明选取正确的模型对训练结果的影响是较大的。在卷积模型中,通过扩大图片分辨率,增加卷积层数与训练轮数,并添加如批次标准化层、数据增强层等技术手段,辅以记录最优值、减少学习率、早停等回调措施,可以在同种模型上获得更优的效果。
心得体会
结论
本次人脸图像性别分类是《机器学习》课程的大作业。在尝试完成这次大作业之前,我对机器学习的了解还十分模糊,仅仅停留在书本知识的层面上。我对Python的理解也加深了,原先只会一些简单的数值运算与画图操作,现在对pip的使用更加熟悉了。经过本次实验,我第一次动手实践了机器学习在实际中的应用。
我本科专业是通信工程,对机器学习并没有基础,因此在实现本次实验中采用了深度学习框架Tensorflow。按照Tensorflow官网上的教程,安装好了对应的显卡驱动和CUDA工具包,并在Pycharm创建的虚拟环境中使用pip安装了Tensorflow。然后根据Tensorflow官网上的对Fashion MNIST进行分类的示例,通过Jupiter Notebook一步一步地了解了做图像分类的一般流程。
首先需要加载图片,教程中是直接从Keras数据集中获取,而用到我们的大作业上就出现了问题。我又复习了Python的基础知识,找到了遍历文件夹下所有文件的方法,但又发生了问题。Windows下读取文件是根据“1.jpg,10.jpg,100.jpg…”的顺序来读的,而不是根据数字的递增来读取,如果直接遍历文件名会导致和标签无法对应,最后采用了从1到 18000在for循环中读取。
本次实验提供给我们的图片为200 × \times × 200像素3通道的RGB图片,共23708张。首先考虑的是直接读取而不进行压缩,结果电脑内存瞬间飙升到30GB,然后提示内存不足。因此考虑将图片压缩到和教程中一样的大小20 × \times × 20像素,并把所有图片都存在一个list中。然后对样本的特征进行一些确认,如shape,确认是否所需的图片全部加载以及对应的标签是否正确。
接下来对数据进行预处理,由于默认读入图片后,在矩阵中保存的值是0~255,不利于后续的处理,我们需要对其除以255.0进行归一化处理。然后进行数据可视化,从数据集中随机选择25张图片进行显示,并标出它们的标签。随后我们可以开始构建模型了,首先参考了教程中的全连接模型,由于是二分类问题,将输出层的神经元数目从10改成2。编译采用adam优化,交叉熵作为损失函数。
对构建的模型进行编译,指定编译轮数后开始训练。训练完成后,使用生成的模型对验证集中的图片进行预测,由于使用softmax函数优化,输出的结果是每个标签的概率值。由于我们需要最终提交的csv文件中是以0、1标识男和女,所以需要比较两个概率,将较大的值输出为1,较小的值输出为0。最后读取test.csv中的id,将预测的标签值写入第二列。还可以对验证集的验证结果进行可视化,显示出其中几张图片,对比预测标签和实际标签,从而评价训练的效果。
经过调参后,训练的效果提升不明显,意识到需要更换模型。通过查阅资料,发现卷积神经网络对于图像分类问题比较擅长。于是更换模型到卷积神经网络,但训练网络的时候出现了问题,提示第一层卷积层输入的shape与预期的不一致。这是因为卷积需要四维向量,而我们读取灰度图片的时候丢失了RGB通道,因此需要用reshape将图片矩阵扩充一个维度。
通过CNN得到比较好的结果后,意识到可以继续增加卷积层的深度,并用一些如批次标准化层来减少过拟合。还通过数据增加技术利用已有的训练集,通过对称、旋转和变形等手段,获得了更加丰富的训练数据。在模型中还添加了回调函数,实现了记录最优值、降低学习率和早停,从而使获得的模型更加契合。
经过本次实验,我学会了使用机器学习解决实际问题的整个流程,掌握了Tensorflow深度学习框架的基本使用,并明白了调参和优化模型的方法,从而实现了理论知识和实际操作相结合。
展望
本实验在以下几个方面还可以加以修改与完善,如:
- 本实验提供的数据集中存在诸多干扰,有些图片的男女标签标错,男标记成1,女标记成0;有些并不是人脸的图片也被放入测试集中,如只包含眼睛和鼻子的图片;在测试集中也存在许多无法得出正确预测结果的图片,如蓝色牛仔裤、随机的数字标签、手绘人脸和一个奶奶抱着一个男孩(图片中同时存在男和女)等。对于测试集中的异常图片,由于必须得出一个预测结果,我们无能为力。但是对于训练集中的异常图片,我们可以采取一些手段。首先是通过人工检查的方式,识别标签标错的图片将其改正,并将不包含人脸特征的图片剔除出去。但对于包含18000张图片的训练集来说,这并不是一件容易的事。其次,我们可以利用一些数据清洗的手段,比如异常检测。先用训练集中一部分得到人工验证后的图片进行训练,然后再对训练集中剩余的图片进行预测,如果得到的标签和train.csv中不一样,则表明这是标签标错的图片,将其改正。然后利用异常检测手段,把离群值较大(不是人脸)的图片从样本空间中清除。这样便可以减轻异常样本对模型的干扰,从而提升模型的准确性。本实验使用初步得到的模型对训练集进行预测,对预测标签和人工标签不同的图片进行人工检查。并对标签进行修正,还剔除了7张不包含人脸的图片,最后剩下17993张图片。
- 本实验提供的图片分辨率均为200 × \times × 200像素,为了矩阵操作,需扩充到200 × \times × 200 × \times × 1。其中训练集有18000张图片,测试集有5708张图片。将23708张图片同时读入到内存中,将产生一个23708 × \times × 200 × \times × 200 × \times × 1的矩阵,展平后变为23708 × \times × 40000,其中每个元素均为float32类型,理论上会占用3.53GB的内存,如果为RGB三通道的图片,将占用10.6GB的内存。实际上,前者将占用多达30GB的内存,由于我的电脑只安装了8GB的内存,因此运行起来特别吃力,全靠虚拟内存。如果采用三通道方式读取,则读取图片过程中提示内存不足。考虑到训练准确度与计算资源消耗的关系,首先将图片压缩到28 × \times × 28,同MNIST数据集。在这种情况下,读取所有图片实际只占用了3GB的内存,训练的速度也很快(2ms一个batch),但最终得到的精度不是很高。最后折衷考虑,采用三通道方式读取图片,将分辨率定为100 × \times × 100像素。所以如果能够利用大内存的专门跑深度学习的机器,完全可以不压缩图片,从而不丢失原始图片中的信息。
本次实验是我在机器学习实际应用中的第一次尝试,由于一些限制还有很多不足的地方。在以后的学习中,将充分总结从本次实验中得到的经验与教训,从而获得更好的成果。
参考文献
- 王艳. 基于深度神经网络的人脸验证[D].北京邮电大学,2019.
- 邱阳. 基于卷积神经网络的人脸个体与性别识别的研究[D].江西理工大学,2019.
- 黄敏强. 基于深度学习的人脸性别识别的研究与实现[D].深圳大学,2018.
- 陈济楠,李少波,高宗,李政杰,杨静.基于改进CNN的年龄和性别识别[J].计算机工程与应用,2018,54(16):135-139+175.
- 张浩. 基于深度学习模型的人脸性别识别方法研究[D].北京工业大学,2016.
- 黄勇. 基于人脸图像的性别识别研究[D].电子科技大学,2016.
- 产文涛. 基于卷积神经网络的人脸表情和性别识别[D].安徽大学,2016.
- 蒋雨欣,李松斌,刘鹏,戴琼兴.基于多特征深度学习的人脸性别识别[J].计算机工程与设计,2016,37(01):226-231.
- Tang Jiexiong, Deng Chenwei, Huang Guang-Bin. Extreme Learning Machine for Multilayer Perceptron… 2016, 27(4):809-21.
- Smith P , Chen C . Transfer Learning with Deep CNNs for Gender Recognition and Age Estimation[C]// 2018 IEEE International Conference on Big Data (Big Data). IEEE, 2019.
