人工智能导论——A*算法实验

一、实验目的：

熟悉和掌握启发式搜索的定义、估价函数和算法过程，并利用A*算法求解N数码难题，理解求解流程和搜索顺序。

二、实验原理：

A*算法是一种启发式图搜索算法，其特点在于对估价函数的定义上。对于一般的启发式图搜索，总是选择估价函数f值最小的节点作为扩展节点。因此，f是根据需要找到一条最小代价路径的观点来估算节点的，所以，可考虑每个节点n的估价函数值为两个分量：从起始节点到节点n的实际代价以及从节点n到达目标节点的估价代价。

A*算法中，若对所有的x存在h(x)≤h*(x),则称h(x)为的下限，表示某种偏于保守的估计。采用的下限h(x)为启发函数的A算法，称为A*算法，其中限制：h(x)≤h*(x)十分重要，它能保证A*算法找到最优解。在本问题中，g(x)相对容易得到，就是从初始节点到当前节点的路径代价，即当前节点在搜索树中的深度。关键在于启发函数h(x)的选择，A*算法的搜索效率很大程度上取决于估价函数h(x)。一般而言，满足h(x)≤h*(x)前提下，h(x)的值越大越好，说明其携带的启发性信息越多，A*算法搜索时扩展的节点就越少，搜索效率就越高。

传统的BFS是选取当前节点在搜索树中的深度作为g(x)，但没有使用启发函数h(x)，在找到目标状态之前盲目搜索，生成了过多的节点，因此搜索效率相对较低。

本实验分别使用不在位的元素个数和曼哈顿距离作为启发函数h(x)。每次从open表中选取时，优先选取估价函数最小的状态来扩展。

A*算法的估价函数可表示为：

    f'(n) = g'(n) + h'(n) 

这里，f'(n)是估价函数，g'(n)是起点到终点的最短路径值（也称为最小耗费或最小代价），h'(n)是n到目标的最短路经的启发值。由于这个f'(n)其实是无法预先知道的，所以实际上使用的是下面的估价函数：

f(n) = g(n) + h(n) 

其中g(n)是从初始结点到节点n的实际代价，h(n)是从结点n到目标结点

的最佳路径的估计代价。在这里主要是h(n)体现了搜索的启发信息，因为g(n)是已知的。用f(n)作为f'(n)的近似，也就是用g(n)代替g'(n)，h(n)代替h'(n)。这样必须满足两个条件：

(1)g(n)>=g'(n)（大多数情况下都是满足的，可以不用考虑），且f必须保持单调递增。

(2)h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h'(n);第

二点特别的重要。可以证明应用这样的估价函数是可以找到最短路径的。

具体步骤：从初始状态S_0出发，分别采用不同的操作符作用于生成新的状态x并将其加入open表中（对应到状态空间图中便是根节点生成新的子节点n） ,接着从open表中按照某种限制或策略选择一个状态x使操作符作用于x又生成了新的状态并加入open表中(状态空间图中相应也产生了新的子节点)，如此不断重复直到生成目标状态。

对于以上所述的“某种策略”，在图搜索过程中，若该策略是依据进行排序并选取最小的估价值，则称该过程为A算法。

三、实验内容：

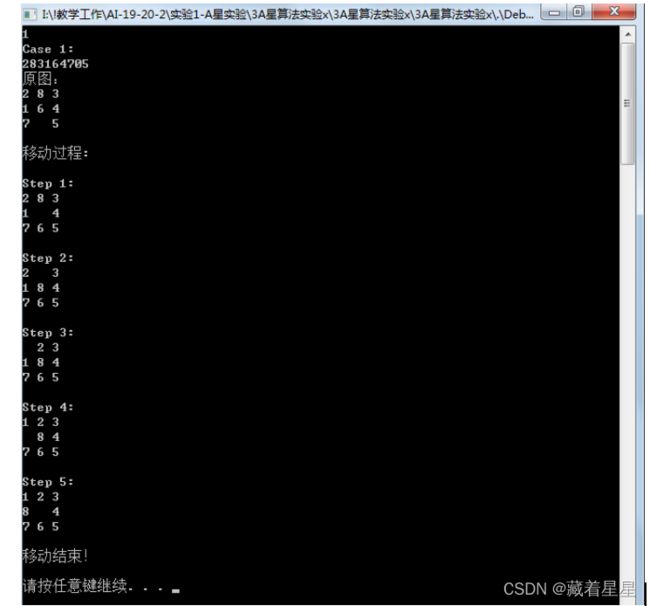
1       参考A*算法核心代码（原程序输出如下图1），以8数码问题为例实现A*算法的求解程序，要求设计两种不同的估价函数。

两种启发函数h(x)：

①不在位的元素个数

int calw(string s)     //计算该状态的不在位数h(n)

{

int re=0;

for(int i=0;i<9;i++) if(s[i]!=t[i]) re++;

return re;

}

②曼哈顿距离

int distance(string s) {

int count=0,begin[3][3],end[3][3];           //count记录所有棋子移动到正确位置需要的步数

for(int i = 0; i < 8; i++){

begin[i/3][i%3]=s[i];

end[i/3][i%3]=t[i];

}

for(int i = 0; i < 3; i++)   //检查当前图形的正确度

for(int j = 0; j < 3; j++)

{

if(begin[i][j] == 0)

continue;

else if(begin[i][j] != end[i][j])

{

for(int k=0; k<3; k++)

for(int w=0; w<3; w++)

if(begin[i][j] == end[k][w])

count = count + fabs(i-k*1.0) + fabs(j-w*1.0);

}

}

return count ;

}

图1 原程序输出

 

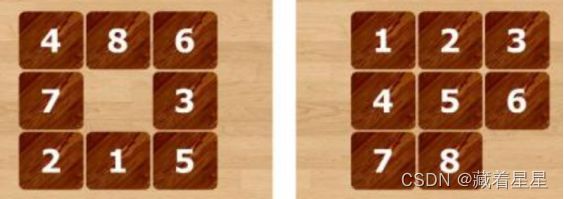
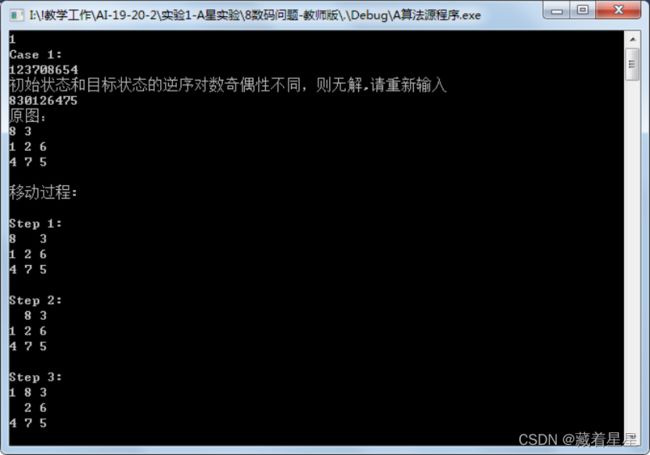
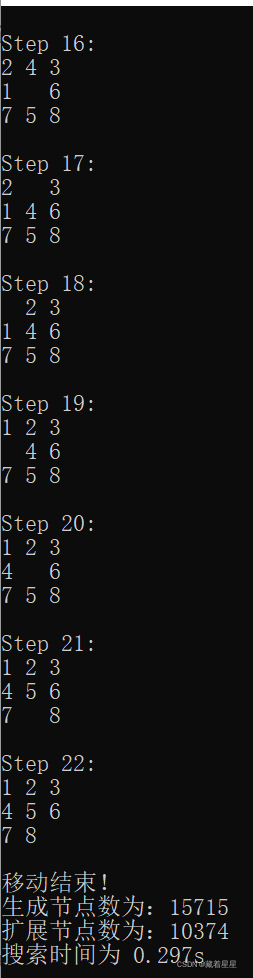
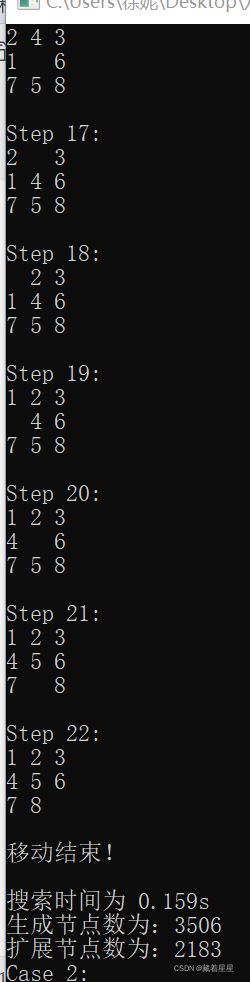
2       在求解8数码问题的A*算法程序中，增加初始状态和目标状态逆序对数奇偶性判断，然后设置相同的初始状态和目标状态（如下图2所示），针对不同的估价函数，求得问题的解，并比较它们对搜索算法性能的影响，包括扩展节点数、生成节点数等，参考输出如下图3所示。

计算逆序对：

int  num(string s){

int a = 0;

for (int i = 0; i < 9; i++){

if (s[i] == '0')

continue;

for (int j = i+1; j < 9; j++)

    {

if (s[j] == '0')continue;

if (s[i]>s[j]) a++;}

}

return a;

}

若逆序对的奇偶性不一样，则返回报错（写在solve函数中）：

int k1=num(t);

int k2=num(p.s);

if(k1%2 != k2%2)

    {cout<<"有错"<

    return -1;

 }

目标状态设定：

const string t="123456780";

初始状态：

“486703215”

         

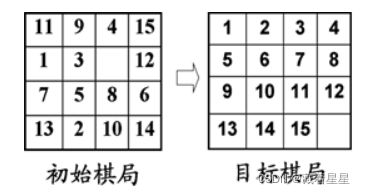
                                                     初始状态              目标状态

                                                                  图2

不同启发函数性能比较如表2

表2不同启发函数比较

	启发函数h(n)
	不在位数	曼哈顿距离	广度优先（0）
初始状态	486703215	486703215	486703215
目标状态	123456780	123456780	123456780
最优解
扩展节点数	10374	2183	102659
生成节点数	15715	3506	123849
运行时间	0.297s	0.159s	1.742s

3  对于8数码问题，设置与上述2相同的初始状态和目标状态，用宽度优先搜索算法（即令估计代价h(n)＝0的A*算法）求得问题的解，以及搜索过程中的扩展节点数、生成节点数。

即：h(n)=0

程序设定：p.w=0;

用宽度优先进行搜索的结果如上表。

1. 参考A*算法核心代码，试修改成能求解15数码问题的代码，15数码问题的初始状态（初始棋局）和目标状态（目标棋局）如下，要求给出问题的解，以及搜索过程中的扩展节点数、生成节点数。

因为两位数的数字输出不太方便，把[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0]改为[

A,B,C,D,E,F,G,H,I,J,K,L,M,N,O]，输入依旧以数字输入。

例如：11 9 4 15 1 3 0 12 7 5 8 6 13 2 10 14

5 1 3 4 2 6 7 8 9 10 12 0 13 14 11 15

运行了很久，发现用不在位数做启发函数，运行不出来。

用曼哈顿距离做启发函数，还是比较快的。

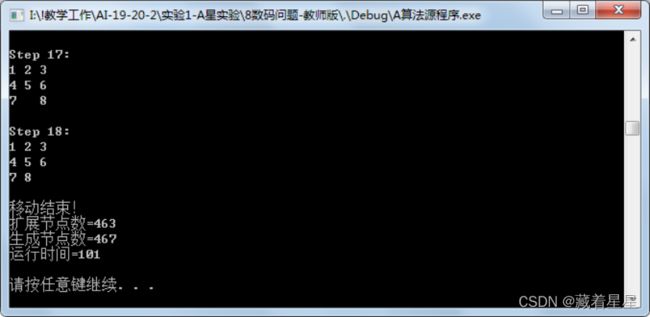
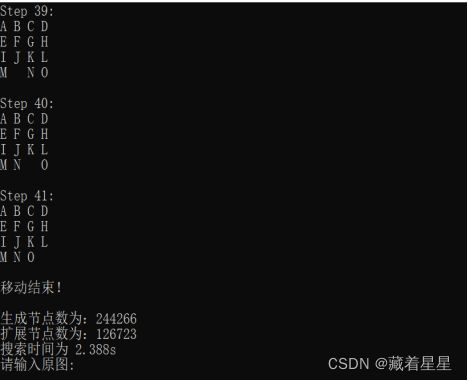
试验结果如图4   

                     

                     

               

图4 15数码搜索结果

可知：生成节点数为：244266

      扩展节点数为：126723

      搜索时间为：  2.388s

5数码修改的部分代码：

 

6提交实验报告和源程序。

四、实验结果： 

1        在求解8数码问题的A*算法程序中，增加初始状态和目标状态逆序对数奇偶性判断是否有解，然后设置相同的初始状态和目标状态，针对不同的估价函数，求得问题的解，并比较它们对搜索算法性能的影响，包括扩展节点数、生成节点数等。

在相同输入和目标情况下，结果比较如表3（来源表2）

表3不同估价函数结果比较

估价函数	不在位数	曼哈顿距离	宽度优先
扩展节点数	10374	2183	102659
生成节点数	15715	3506	123849
运行时间	0.297s	0.159s	1.742s

扩展节点为count1,生成节点为count2，实验结果和要求的节点数均在实验内容2中。

输入和目标相同时，可得曼哈顿距离做估价函数比不在位数做估价函数更好，曼哈顿距离做估价函数的生成节点和扩展节点只有两三千，不在位数做估价函数的生成节点和扩展节点都超过了一万，可知搜索空间也少很多，曼哈顿做估价函数的效率高很多。

2        根据宽度优先搜索算法和A*算法，分析启发式搜索的特点。

广度优先搜索法在有解的情形总能保证搜索到最短路经，也就是移动最少步数的路径。但广度优先搜索法的最大问题在于搜索的结点数量太多，因为在广度优先搜索法中，每一个可能扩展出的结点都是搜索的对象。随着结点在搜索树上的深度增大，搜索的结点数会很快增长，并以指数形式扩张，从而所需的存储空间和搜索花费的时间也会成倍增长。

我们可以发现采用A*算法求解八数码问题时间以及搜索的节点数目远远小于采用宽度优先搜索算法，这说明对于八数码问题，选用的启发性信息有利于搜索效率的提高。

3          对比15数码和8数码问题，试分析A*算法求解不同问题规模的性能。

当使用不在位数做估价函数改进8数码代码，程序运行很长时间也没有结果。所以若问题规模过大，使用A星算法时要设计好估价函数，设计的不合适就会使搜索空间太大了，一直没有结果。本实验中采用曼哈顿距离做估价函数，搜索还是很快的，有20多万的生成节点和10多万的扩展节点，使用曼哈顿做估价函数效率很高，时间也只有2s多。

五实验总结：

通过这次实验，使我对启发式搜索算法有了更进一步的理解，尤其是对估价函数的应用和设计上有了一定的体会，一个合适高效的估价函数对于启发式搜索算法来说是十分重要的。