李沐基于Pytorch的深度学习笔记(7)-线性回归的基本实现(附代码)
1 线性回归的实现
这里我参考了这两篇博客
线性回归及python代码实现___zachary的博客-CSDN博客_python线性回归代码
python机器学习手写算法系列——线性回归_juwikuang的专栏-CSDN博客_python 机器学习
由于李沐老师的课程中使用的d2l和我安装的部分库存在冲突,所以我没有使用他的方法进行线性回归。
![]()
整体的步骤和我们上面讲到的一个模型步骤是一样的。
1.1 数据生成
import pandas as pd
import random
import matplotlib
import matplotlib.pyplot as plt
import os
import torchvision
from torchvision import transforms
#设置随机的算法初始值
np.random.seed(300)
#生成size个符合均分布的浮点数,取值范围【low, high】,默认的取值范围是【0, 1.0】
data_size = 100
x = np.random.uniform(low = 1.0, high = 10.0, size = data_size)
y = x * 20 + 10 + np.random.normal(loc = 0.0, scale = 10.0, size = data_size)
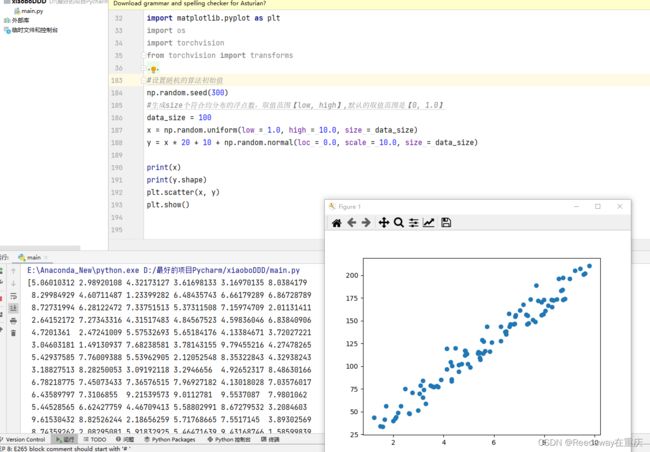
print(x)
print(y.shape)
plt.scatter(x, y)
plt.show()这里进行一部分的代码解释:
np.random.seed()是生成随机种子数,这些随机种子是有顺序的,具体的可以参照下面这篇博文:
np.random.seed()随机数种子_程序员_Iverson的博客-CSDN博客
numpy.random.uniform(low,high,size)从一个均匀分布[low,high)中随机采样,注意定义域是左闭右开,即包含low,不包含high:
Nump中 np.random.uniform()函数用法_lemonxiaoxiao的博客-CSDN博客_np.random.uniform函数怎么用
numpy.random.normal(loc=0.0, scale=1.0, size=None)意思是一个正态分布,具体参考下面这篇博文:
np.random.normal()详解_java_pythons的博客-CSDN博客_np.random.normal
plt的应用就不说了,plt.scatter()是可视化的散点图,plt.show()就是直接展示。
1.2 训练集和测试集划分
shuffled_index = np.random.permutation(data_size)
x = x[shuffled_index]
y = y[shuffled_index]
split_index = int(data_size * 0.75)
x_train = x[:split_index]
y_train = y[:split_index]
x_test = x[split_index:]
y_test = y[split_index:]random.random()用于生成一个0到1的随机符点数: 0 <= n < 1.0
但是由于数值的类型问题,这里我看了下相关博文,发现使用的是random.permutation()这个函数
np.random.permutation()函数的使用_zhlw_199008的博客-CSDN博客_random.permutation
从线性回归(Linear regression)到逻辑回归(logistic regression)再到Softmax_谷雨的博客-CSDN博客
1.3 定义线性回归类
class LinerRegression():
def __init__(self, learning_rate=0.01, max_iter=100, seed=None):
np.random.seed(seed)
self.lr = learning_rate
self.max_iter = max_iter
self.a = np.random.normal(1, 0.1)
self.b = np.random.normal(1, 0.1)
self.loss_arr = []
def fit(self, x, y):
self.x = x
self.y = y
for i in range(self.max_iter):
self._train_step()
self.loss_arr.append(self.loss())
def _f(self, x, a, b):
"""一元线性函数"""
return x * a + b
def predict(self, x=None):
"""预测"""
if x is None:
x = self.x
y_pred = self._f(x, self.a, self.b)
return y_pred
def loss(self, y_true=None, y_pred=None):
"""损失"""
if y_true is None or y_pred is None:
y_true = self.y
y_pred = self.predict(self.x)
return np.mean((y_true - y_pred)**2)
def _calc_gradient(self):
"""梯度"""
d_a = np.mean((self.x * self.a + self.b - self.y) * self.x)
d_b = np.mean(self.x * self.a + self.b - self.y)
print(d_a, d_b)
return d_a, d_b
def _train_step(self):
"""训练频度"""
d_a, d_b = self._calc_gradient()
self.a = self.a - self.lr * d_a
self.b = self.b - self.lr * d_b
return self.a, self.b
关于里面每个函数的用法,其实有些我没有特别看懂。特别是fit函数,有些点方法我是没有查到的,哈哈哈。
1.4 训练与展示
之后我们开始训练:
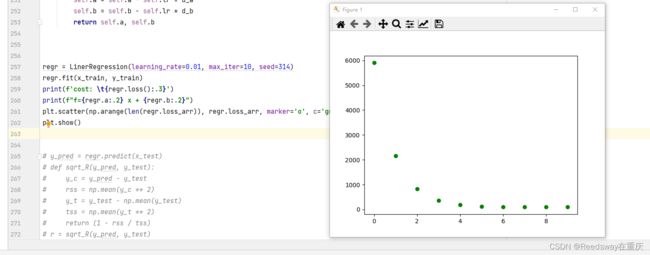
regr = LinerRegression(learning_rate=0.01, max_iter=10, seed=314)
regr.fit(x_train, y_train)
print(f'cost: \t{regr.loss():.3}')
print(f"f={regr.a:.2} x + {regr.b:.2}")
plt.scatter(np.arange(len(regr.loss_arr)), regr.loss_arr, marker='o', c='green')
plt.show()1.5 进行评估
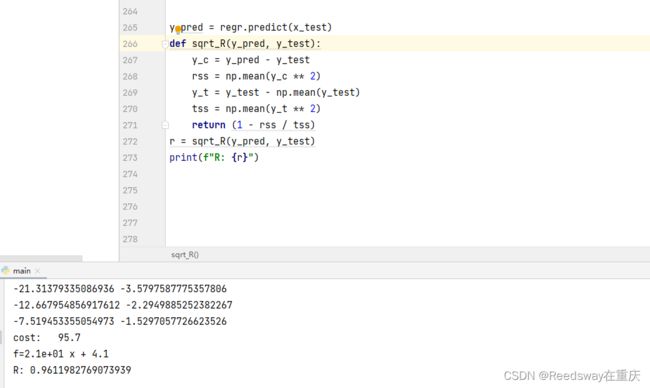
y_pred = regr.predict(x_test)
def sqrt_R(y_pred, y_test):
y_c = y_pred - y_test
rss = np.mean(y_c ** 2)
y_t = y_test - np.mean(y_test)
tss = np.mean(y_t ** 2)
return (1 - rss / tss)
r = sqrt_R(y_pred, y_test)
print(f"R: {r}")