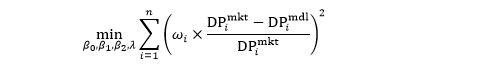债券收益率曲线构建
本文有 2677 字,26 图表截屏
建议阅读 30 分钟
0
引言
本文是金融工程系列的第十四篇
弄清量化金融十大话题 (上)
弄清量化金融十大话题 (下)
金融工程高度概览
日期生成
变量计算
模型校正
曲线构建 I - 单曲线
曲线构建 II - 多曲线 (基差)
曲线构建 III - 多曲线方法 (抵押品)
债券收益率曲线构建
测度转换 (上) - 等价物转换
测度转换 (下) - 漂移项转换
产品估值理论
产品估值 - 解析法和数值积分法 (CF)
产品估值 - 偏微分方程有限差分法 (PDE-FD)
产品估值 - 蒙特卡洛模拟法 (MC)
产品风险理论 (AAD)
风险计量 - 敏感度 (Greeks & Sensitivities)
风险计量 - 风险价值 (VaR)
价值调整 - 凸性调整
价值调整 - Quanto 调整
价值调整 - 时间调整
价值调整 - CVA
价值调整 - DVA
价值调整 - FVA
价值调整 - MVA
价值调整 - KVA
在构建掉期曲线(swap curve)时,每个标准年限都对应着一个市场报价,这样我们通常可以完美拟合出市场上它们的价格,但在构建债券曲线(bond curve)时,市场报价的债券到期日各不相同,我们只能近似拟合出它们的价格。
本帖我们就用 Nelson-Siegel (NS) 模型来拟合欧元区金融债 AA 评级的收益率曲线。结构如下:
介绍 NS 模型
介绍拟合方法
展示代码产出
1
Nelson-Seigel 模型
Nelson-Siegel (NS) 模型最早由 Nelson 和 Siegel 于 1987 年提出,该模型适用于利率期限结构分析。NS 模型中有四个参数,每个都有自身的经济含义,而且不同参数值能描述不同情境下的利率曲线的变动情况。
瞬时远期利率
首先 NS 模型制定了瞬时远期利率(instantaneous forward rates)的形式:
该模型有四个参数 β0, β1, β2, λ,其中 τ = T - t 是到期年限,λ > 0。
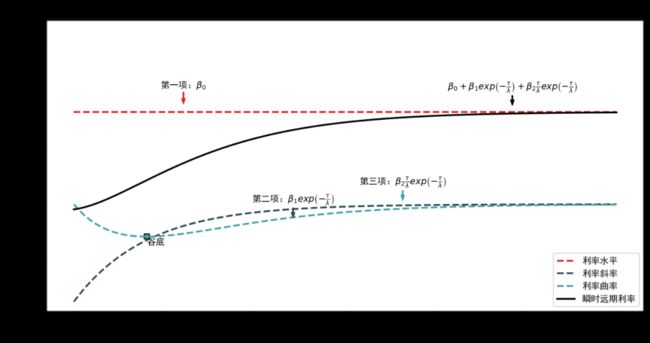
瞬时远期利率 f(t, T) 里面有三项:
第一项 β0 是当 τ 趋近无穷大时的远期利率,因此 β0= f(∞)。
第二项是个单调函数,当 β1> 0 时递减,当 β1 < 0 时递增。
第三项是个非单调函数,可以产生 hump。
当 τ 趋近零时,第二项趋近于 β1,第三项趋近于 0,因此 f(0) = β0 + β1。
我用第三节拟合出来的参数
β0 = 0.03397838
β1 = -0.03586764
β2 = -0.03236844
λ = 4.03815169
来分解 NS 模型中的三项,得到下图:
注意 β1 是负数,因此第二项是增函数,注意蓝线缓缓向上。β2 也是负数,因此第三项是先减后增,有个谷底(而不是峰顶)。
即期利率
根据即期利率和瞬时远期利率之间的关系,我们求积分得到
即期利率 R(T – t) 里面也有三项。
第一项 β0 是当 τ 趋近无穷大时的即期利率,因此 β0 =R(∞)。
第二项是个单调函数,当 β1> 0 时递减,当 β1 < 0 时递增。
第三项是个非单调函数,可以产生 hump。
当 τ 趋近零时,第二项趋近于 β1,第三项趋近于 0,因此 R(0) = β0 + β1。
将上面等式写成因子形式
这样容易看出:
β0 的因子载荷是常数,对于对所有期限利率的影响是相同的,因此 β0 可控制利率水平(level),它的变动会使得收益率曲线发生水平上下移动。
β1 的因子载荷是单调递减,从1 很快的衰减到 0,这表明 β1 对短端利率的影响较大,因此 β1 可控制曲线斜率(slope),影响着利率曲线的斜率程度。
β2 的因子载荷先增后减,从 0 增到 1 再减到 0,这表明 β2 对利率曲线的短端和长端影响较弱,对中端的影响较大,因此 β2 控制曲线曲率(curvature)。
τ 是 β1 和 β2 的因子载荷的衰减速度,该值越大衰减越快。
用 NS 模型可以模拟利率曲线的最基本的三种形式:平移、斜率和曲率,足够了。在 NS 基础上,Svensson 在 1994 年做了改进,为了能多模拟一个 hump 形状而增加了两个参数。该模型下的瞬时远期利率的形式为
同时求积分我们可以得到其即期利率:
Svensson 模型可以处理两个 hump,模型表达能力更强了,但是对于简单类型的利率曲线也更容易过拟合。我在实际操作中没有发现它显著强于 NS 模型,而且在拟合 10 几年的债券收益率曲线时,Svensson 模型更容易发生参数跳跃的情形,这不是我们希望看到的结果。因此我偏向于用 NS 模型。
2
拟合方法
在某个行业某个评级下都有一系列交易的债券,根据其市场价格或收益率我们可以拟合出来一条收益率曲线。在某个观测日(假设为 2020 年 1 月 24 日),拿欧元区 AA 金融行业(EUR Financial AA)举例,我们有如下市场信息:
拟合曲线就是最小化以下的目标函数,它是所有 n 个交易债券的市场价格和模型价格之差的加权平方:
其中 DPimkt 是债券的市场全价(dirty price),它等于市场净价(clean price)加上累积利息(accrual interest)
![]()
而 DPimdl 是债券的模型全价,其表达式为
其中折现因子为
权重可以是等权重,也可以是修正久期(modified duration)的倒数:
其中修正久期等于麦考利久期(Macaulay duration)除以 1 加上到期收益率
一些选取初始值的技巧包括:
根据 R(∞)= β0, R(0) = β0+ β1,我们可以找出交易债券中到期最短和最长的两个收益率 yS 和 yL,然后将 β0 的初始值设置为 yL,将 β1 的初始值设置为 yS – yL。
将 β2 的初始值设置为 0,假设曲线一开始没有 hump。
对于 λ 创建一个初始值网格(grid),在上下界 [λmin, λmax] 中平均分成 5 段,λmin 通可定为 1/30,而 λmax 是在最长到期日 τL 下的 hump 对应极值的 λ。
3
代码展示
引入所有需要的包:
NS 模型下的核心函数(计算瞬时远期利率、即期利率、折现因子、离散远期利率):
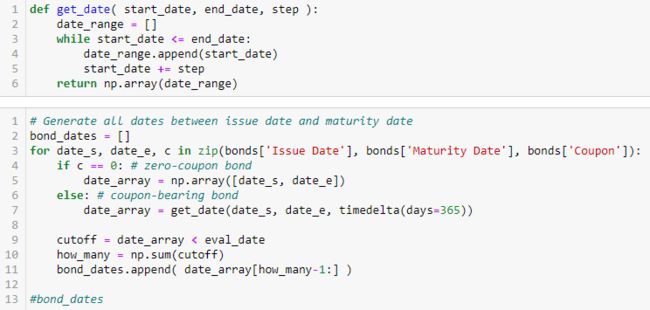
读取数据,将债券发行日和到期日用 pd.to_datetime() 转成专门的日期格式。
生成每个债券的付息日(假设每年付息一次,具体付息频率要看 termsheet)
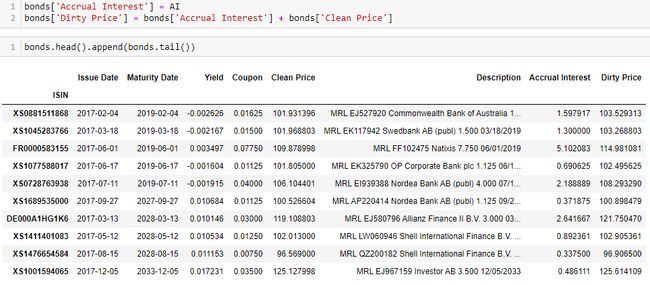
生成每个债券的到期日期限 T、累积利息 AI、付息日年限 year_facr、现金流 cashflows 和修正久期 MD:
更新 DataFrame bonds。
定义目标函数,用修正久期的倒数加权。
核心 NS 模型拟合函数,用 scipy.optimize 一把梭就完了。
运行结果,速度还挺快,1-2 秒钟就出来了。
可视化一下结果,注意红框的市场收益率和黑点的模型收益率蛮接近。
4
总结
本文只展示了拟合某行业某评级一天的收益率曲线,在实际操作中,我们做的事拟合各行业各评级几年的收益率曲线,这时候有三个问题要注意:
去掉交易量不活跃的报价(比较主观)
曲线近端的拟合:引入短期限的 IBOR
模型参数的跳跃:NS 模型加限制条件,目标函数加惩罚项
Stay Tuned!
![]()