SM2 (含SM3、SM4)国密算法工具QT版，彻底搞懂sm2算法的使用

网上有很多网友问算法SM2怎么使用？什么是压缩公钥和非压缩公钥？xB和yB这参数是什么？怎么使用SM2做加解密？如何签名和验签？有没有工具来验证下？

这里分享个自己用QT造的一个小工具，简单好用，同时也增加支持了SM3、SM4国密算法。且有详细的过程日志，可以保存为文件。用来对SM2国密算法做加解密和签名，验签,秘钥生成再合适不过了。

需要工具的和使用上的疑问的都可以在留言区留言和评论，工具免费提供。也可以在个人的csdn资源中下载。

完整版的下载：

sm2国密算法工具完整版，包含sm2,sm3和sm4-QT文档类资源-CSDN下载

工具源码的下载：

sm2国密算法加解密、签名、验签QT工具源码（包含sm2,sm3和sm4源代码）-C文档类资源-CSDN下载

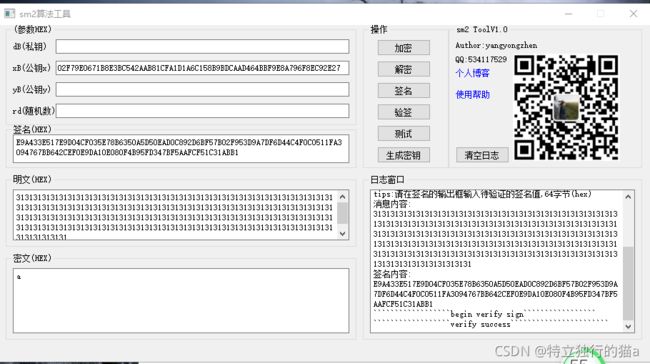
加密，解密验证：

其中xB为公钥，如果是压缩公钥，这里填33字节的16进制的压缩公钥，yB不用填，会自动计算得到。如果是非压缩公钥，则xB和yB都需要输入，分别填非压缩公钥的前32字节和后32字节。

其实说白点儿xB和yB合起来才是一串完整的非压缩公钥，只是把公钥分成了两段罢了。

况且，如果是压缩公钥，只需要32字节的xB就够了。哦不，前面的02或03可不能少，要不没法求得yB这后半段公钥。至于为啥公钥要搞成x,y两段，是因为公钥是椭圆曲线上的一个点，一个点包含(x，y)两个分量，这才确定了一个坐标。

为啥给定了x就能求得y,给定y能否求得x呢？当然了，根据椭圆曲线方程：y^2=x^3+ax+b，

a,b都是常数是已知的，给了x就能得到y,给定y就能得到x。有时候压缩公钥别人会给02开头的，有时候会给03开头的。看到这个公式知道了吧，02开头的相当于给你了x,03开头的相当于给你了y.

不压缩的公钥相当于直接给你了(x,y)一个完整坐标。

再说下那个随机数，它是固定长度的32个字节。这随机数也是为了安全。在加密时有用，解密时用不到。这个工具中，加密时之所以随时数为非必填，代码里给你指定了固定的一个值。当然，你可以输入和改变这个随机数。而且，随时数不同，加密后的内容是不同的。但是，解密时，只要私钥pB正确，都能正确的解密出明文，这厉害吧。

日志窗口中可以看到详细的加密，解密日志。 

签名验证：

其中，xB位置输入sm2的压缩公钥，长度为33字节。最前面的02或03代表压缩的参数。明文处输入消息内容，签名的输入框输入待验证的签名信息（签名信息是定长，为64个字节）。点击验签按钮。最后看到日志窗口提示 verify success则是验签成功。

签名和验签的算法过程：

签名过程：
以签名者A为例，计算 ZA=H256(ENTLA ∥ IDA ∥ a ∥ b ∥ xG ∥ yG ∥ xA ∥ yA)，其中ENTLA是IDA的比特长度转换而成的两个字节；
M' = ZA || M，其中M为待签名消息；
e = H256(M')；
用随机数发生器产生随机数k ∈[1,n-1]；
计算椭圆曲线点(x1,y1)=[k]G；
计算r=(e + x1) mod n，若r=0或r+k=n则返回step 4；
计算s = ((k − r * dA) / (1 + dA)) mod n，若s=0则返回step 4；
输出签名（r,s）；
验签过程：
ZA=H256(ENTLA ∥ IDA ∥ a ∥ b ∥ xG ∥ yG ∥ xA ∥ yA)
M′ =ZA ∥ M；
e = H256(M')；
计算t = (r ′ + s ′ ) mod n， 若t = 0，则验证不通过；
计算椭圆曲线点(x1 , y1 ) = [s']G + [t]PA；
计算R = (e + x1 ) mod n，检验R = r是否成立，若成立则验证通过；否则验证不通过；
后续打算用详细代码来展示这一过程。

上述过程中的那么多字母，如果不明白含义容易看晕。

ENTLA ∥ IDA ∥ a ∥ b ∥ xG ∥ yG ∥ xA ∥ yA拿这串来举例：

ENTLA是长度，占两字节，它可能是个变长。

IDA是，用户ID数据。国密sm2使用的是固定的值"1234567812345678"。

a,b,xG和yG是椭圆曲线算法选定的椭圆曲线参数。后面有说明。这几个都是个固定值。

xA和yA这个就是公钥的前后两段。

代码展示ZA=H256(ENTLA ∥ IDA ∥ a ∥ b ∥ xG ∥ yG ∥ xA ∥ yA)这个过程:

    userid_bitlen = userid_len << 3;
    buf[0] = (userid_bitlen >> 8) & 0xFF;
    buf[1] = userid_bitlen & 0xFF;

    // ENTLA|| IDA|| a|| b|| Gx || Gy || xA|| yA

    memcpy(buf+2, userid, userid_len);
    memcpy(buf+2+userid_len, sm2_par_dig, 128);

    memset(buf+2+userid_len+128, 0, 64);
    memcpy(buf+2+userid_len+128+32-xa_len, xa, 32);
    memcpy(buf+2+userid_len+128+32+32-ya_len, ya, 32);

    sm3(buf, 2+userid_len+128+32+32, e);

密钥对的生成:

选取合适的椭圆曲线参数{p,a,b,Gx,Gy,n}；

用随机数发生器产生整数d ∈ [1,n−2]；

计算点P = (xP,yP) = [d]G；

如果P是无穷远点O，goto step 2；

输出密钥对(d,P)，其中d为私钥，P为公钥。

代码过程：

    ......  
    cinstr(p,cfig->p);
	cinstr(a,cfig->a);
    cinstr(b,cfig->b);
	cinstr(n,cfig->n);
	cinstr(x,cfig->x);
    cinstr(y,cfig->y);
	ecurve_init(a,b,p,MR_PROJECTIVE);
    g = epoint_init();
    epoint_set(x,y,0,g); 
    irand(time(NULL));
    bigrand(n,key1);   私钥db
    ecurve_mult(key1,g,g); //计算Pb
    epoint_get(g,x,y);
    *wxlen = big_to_bytes(32, x, (char *)wx, TRUE);
   	*wylen = big_to_bytes(32, y, (char *)wy, TRUE);
	*privkeylen = big_to_bytes(32, key1, (char *)privkey, TRUE);
    ......

p,a,b,Gx,Gy,n为椭圆曲线参数，国密sm2使用的是以下的值的参数。

p是一个大的质数。a,b是方程中的两个常量。Gx,Gy为基点的x,y坐标。n 是基点G的可倍积阶数。

给定n和P，我们运算Q=nP至少需要一个多项式时间。但是如果反过来呢？如果我们知道Q和P，要反过来得到n呢？该问题被认为是对数问题。感兴趣的可以查下什么是对数问题。

查阅《GMT 0003-2012》这份标准文档，有SM2算法的设计背景知识供解读。

 使用素数域256位椭圆曲线
曲线方程：y^2=x^3+ax+b
曲线参数
 p = FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF 
 a = FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC 
 b = 28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93 
 n = FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF409 39D54123 
 Gx = 32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589 334C74C7 
 Gy = BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0 

需要进一步的了解椭圆曲线算法，可先了解下ECC模型。

 ECC模型
ECC椭圆曲线由很多点组成，这些点由特定的方程式组成的，比如方程式可以是y^2 = x^3 + ax + b，这些点连接起来就是一条曲线，但曲线并不是一个椭圆。

椭圆曲线有个特点，任意两个点能够得到这条椭圆曲线上的另外一点，这个操作称为打点，经过多次（比如d次）打点后，能够生成一个最终点（F）。

在上面的图中，A点称为基点（G）或者生成器。A可以和自己打点从而生成B点，在实际应用的时候，一般有基点就可以了。经过多次打点，就得到了最终点G。

ECC密码学的关键点就在于就算知道具体方程式、基点（G）、最终点（F），也无法知晓一共打点了多少次（d）。

ECC中，打点次数(d)就是私钥，这通常是一个随机数，公钥就是最终点（F)，包含(x，y)两个分量，通常组合成一个数字来传输和存储。

ECC由方程式（比如a、b这样的方程式参数）、基点（G）、质数（P）组成。理论上方程式和各种参数组合可以是任意的，但是在密码学中，为了安全，系统预先定义了一系列的曲线，称为命名曲线（name curve），比如secp256k1就是一个命名曲线。对于开发者而言，在使用ECC密码学的时候，就是选择具体的命名曲线。

SM2算法是ECC算法的一种，相当于是设计了一条ECC命名曲线。

为什么要大力推广国密算法，当然是因为安全了。以下这段摘自网上：

摘自：https://www.cnblogs.com/gzhlt/p/10270913.html

椭圆曲线算法安全性，现状，运用

目前椭圆曲线应用的范围越来越广，在BTC，ETH，EOS，莱特币，DASH等都有使用。密码学中把正向计算是很容易的，但若要有效的执行反向则很困难的算法叫做陷门函数。在RSA的章节中已经介绍过，RSA会随着因式分解的数字变大而变得越有效率，对于私钥增长的需求决定了RSA并不能算作一个完美的陷门函数。事实证明在椭圆曲线中如果你有两个点，一个最初的点乘以K次到达最终点，在你只知道最终点时找到n和最初点是很难的，这就是一个非常棒的trapdoor函数的基础，最近三十年的研究，数学家还没有找到一个方法证实。密码学家Lenstra引进了“全球安全（Global Security）”的概念：假设破解一个228字节的RSA秘钥需要的能量少于煮沸一勺水的能量。那么破解一个228字节的椭圆曲线秘钥需要煮沸地球上所有水的能量。如果RSA要达到一个同样的安全水平，你需要一个2,380字节的秘钥。

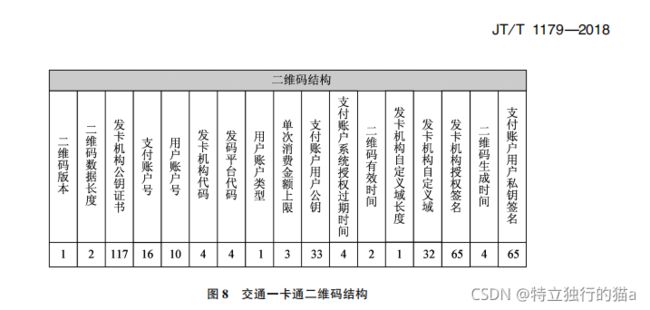
最后，以交通部二维码为例，介绍下签名和验签，及工具的使用：

交通部码结构如上图所示。

原始扫码数据内容：

800149240101000004120102030412990102030404002103C28E9FFBFEBC1D1A38644B009A5019F870425145485BF580DCB096DC80BCA7436A8A847E1963930AD71C8D8509DD7FDA36C413158A4DC0E7DD80530DB4B5E1B4FEDFB3217140F255458320F1C0A92B0D4F154DF22D9FFAEE8404EFDDE0447C733230383833303234353539353434373252484E47544253414654353030303530303101000032031FACA38A116BF843720D1A078845FF7BF87C3E62CC17A06A10BAFAEEB4C896B1618B7155012C0015B5A6772E198F0251F1DFBE9CB251ADE475139D12C7BF714CF436A444CB5474F556EF82699C84EC3C74F5C62C7F69872C3477697E2A09D08BEA0224C23A089259618236D5156EA4FCDBE951017E70B2CF19F0D9A27A6ED1E798B0F85850D32F8FEE0902E458BCEFC2AC1CC7AD99478A680B929476AE1AC0236F691D4A65B044C677834DD886 

二维码解析：

80//二维码版本
0149//二维码长度
//发卡机构公钥证书117字节
240101000004120102030412990102030404002103C28E9FFBFEBC1D1A38644B009A5019F870425145485BF580DCB096DC80BCA7436A8A847E1963930AD71C8D8509DD7FDA36C413158A4DC0E7DD80530DB4B5E1B4FEDFB3217140F255458320F1C0A92B0D4F154DF22D9FFAEE8404EFDDE0447C73
xx3038383330323435353935xxxxxxxx//支付账户号16字节
52484E475442********//用户账户号10字节
35303030 //发卡机构代码
35303031//发码平台代码
01//用户账户类型
000032//单次消费金额上限

//支付账户用户公钥33字节的压缩公钥
031FACA38A116BF843720D1A078845FF7BF87C3E62CC17A06A10BAFAEEB4C896B1
618B7155//授权过期时间
012C//二维码有效时间
00//发卡机构自定义域长度，
15//签名格式
//发卡机构授权签名64字节
B5A6772E198F0251F1DFBE9CB251ADE475139D12C7BF714CF436A444CB5474F556EF82699C84EC3C74F5C62C7F69872C3477697E2A09D08BEA0224C23A089259
618236D5//二维码生成时间
15//签名格式
//支付账户用户私钥签名64字节
6EA4FCDBE951017E70B2CF19F0D9A27A6ED1E798B0F85850D32F8FEE0902E458BCEFC2AC1CC7AD99478A680B929476AE1AC0236F691D4A65B044C677834DD886

使用支付账户用户公钥33字节的压缩公钥对支付账户用户私钥签名进行验证：

总结下交通部乘车二维码的验签，过程也很简单。

总共需要三次验签。

第一步验签，验发卡机构证书的签名，使用从系统后台下载到的根公钥。

第二次验签，验发卡机构授权签名，使用发卡机构公钥证书中的公钥。

第三次验签，验支付装好用户私钥签名，使用支付账户用户公钥。

经过这三次的验签成功，则二维码的合法性通过验证。再结合二维码的有效期和授权过期时间，应用类型，白名单等验证等信息验证，就可以判断是否允许乘车啦。