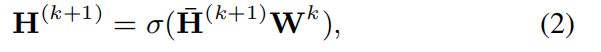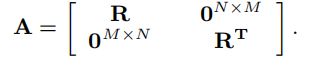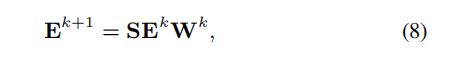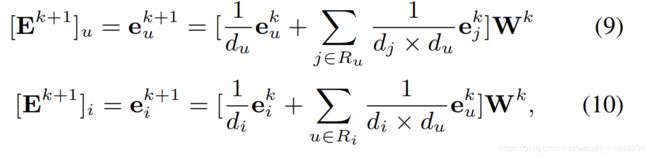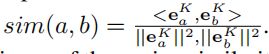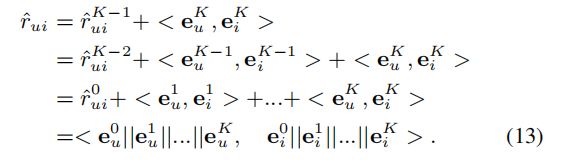【论文笔记】Revisiting graph based collaborative Filtering:一种线性残差图图卷积网络方法
Revisiting Graph based Collaborative Filtering:A Linear Residual Graph Convolutional Network Approach
本文提出了一种使用非线性特征传播和残差结构的GCN网络LR-GCCF用于基于CF的推荐系统,在模型表型上和时间效率上有了一定的提高。
摘要
GCNs通过不断堆叠层数是最好的图表示模型。最近,推荐系统中的协同过滤,一种把用户-物品交互当作二部图来看待的方法,一些研究使用GCNs来建模高阶的协同信号。这些推荐模型相比于传统的模型展示了很好的性能。然而,这些模型由于带着非线性激活并且用在大的用户-物品交互图中是十分难训练的。并且,大多数的GCNs网络由于过平滑问题都不能太深。在本文中,我们从两个方面重新审视了基于GCN的CF模型:1.我们的经验表明,去除非线性会提高推荐性能,这与简单图卷积网络的理论是一致的 2.我们提出了一种专门用于CF的残差网络结构,这可以缓解在用户-用户的稀疏中执行图卷积聚合操作过平滑的问题。
介绍
进几年见证了GCNs的火爆程度,它还有很多变体来应对不同的任务。GCNs的基本思想是迭代地堆叠层数,每一层的操作具体为:1.基于卷积邻域聚合的节点嵌入2.然后对神经网络参数化的节点嵌入进行非线性变换。因此,节点的高阶相似性很容易就被捕捉到了。
在本文中,我们关注把GCNs应用在CF中。CF通过用户-物品过去的数据来提供个性化推荐。事实上,把用户-物品交互矩阵看成一幅图,CF可以转成成图中的边预测问题。近几年来,有很多工作工作关注把GCNs用在协同过滤中,基于GCNs的推荐系统模型也比传统的模型效果好。
与基于GCN的推荐的成功不同,我们讨论两个在GCN仍然没有解决的问题。首先,对于用户和物品的嵌入表示,GCNs使用两步1.通过图卷积操作的邻居聚合2.非线性变换。图卷积操作对聚合邻居信息是十分有用的,但是非线性激活是有必要的吗?其次,现有的大多数模型都只能堆叠少数的几层GCN层。事实上,图卷积操作是一种特殊形式的图拉普拉斯平滑。通过k层的GCNs,拉普拉斯平滑可以把k阶领域的邻居包括在内。因此,由于高层的邻居相互之间变得不可区分,过平滑问题存在于深层模型中。再推荐中限制用户-物品的交互记录,过平滑的问题会变得十分严重,由于训练数据十分稀疏。凭直觉,通过增加层数可以缓解CF中数据稀疏的问题,但是同时也会使节点趋于一致并降低模型表现。如何更好的建模图结构同时规避过平滑的问题仍然备受关注。
为了解决上诉问题,我们重新仿了基于图结构的带着残差图卷积的模型。我们的主要贡献在下面两个方面:1.我们分析了CF与其他图结构任务的独特性,并且说明去掉非线性变换可以增加模型性能的同时降低复杂度,这与最近简化GCNs的理论是一致的。2.为了在迭代过程中缓解过平滑的问题,我们提出了在每层中增加残差连接。因此,用户的独特性将会在底层中被保留,高层的GCN可以关注学习用户的剩余偏好(user's residual preferences),这可以在每个用户的有限的历史中被捕获。这种思想来源于ResNet,我们的工作致力于如何把残差部分的结构融入到用户-物品的交互预测中。我们证明了,我们提出的模型退化成了一个线性模型来通过用户-物品的交互进行预测。总之,与现有的基于GCNs的推荐模型相比,我们提出的模型更容易训练,易于更大的模型。
准备工作和相关工作
![]() ,
,![]() 是点的集合,A是邻接矩阵,
是点的集合,A是邻接矩阵,![]() 表示节点
表示节点![]() 和
和![]() 的边,如果
的边,如果![]() 与
与![]() 之间有边,则
之间有边,则![]() 为1,否则为0。使用
为1,否则为0。使用![]() 来表示节点
来表示节点![]() 的邻居集合。使用
的邻居集合。使用![]() 表示加自环的规范化邻接矩阵,
表示加自环的规范化邻接矩阵,![]() 是加自连通图的邻接矩阵,
是加自连通图的邻接矩阵,![]() 是单位矩阵,
是单位矩阵,![]() 是
是![]() 的度矩阵。
的度矩阵。
图卷积网络
对于节点![]() ,我们使用
,我们使用![]() 表示节点的初始化嵌入表示,它通常是节点
表示节点的初始化嵌入表示,它通常是节点![]() 的特征向量
的特征向量![]() 。在图
。在图![]() 中,GCNs的主要思想是通过堆叠k层网络来循环使用消息传递或特征传递方式学习节点表示。特别地,对节点
中,GCNs的主要思想是通过堆叠k层网络来循环使用消息传递或特征传递方式学习节点表示。特别地,对节点![]() ,通过以下两部递归地计算:特征传播和非线性特征变换。
,通过以下两部递归地计算:特征传播和非线性特征变换。
特征传播
对于节点![]() 特征传播步在中从邻居
特征传播步在中从邻居![]() 和它自己的嵌入表示
和它自己的嵌入表示![]() 聚合嵌入。
聚合嵌入。
早期的工作聚焦在如何建立聚合函数中。由于本文的重点不是设计更复杂的特征聚合函数,所以使用广泛使用的模型:
事实上,给了第![]() 层的特征
层的特征![]() ,特征传播的输出
,特征传播的输出![]() 可以看作是在前一层的拉普拉斯平滑。
可以看作是在前一层的拉普拉斯平滑。
非线性变换
非线性变换是标准的多层感知机,![]() 是一个非线性激活函数:
是一个非线性激活函数:
在k层循环使用上面两个步骤后,在层数k的最后的节点表示为![]() ,对于大多数的节点分类任务,有一个预测函数:
,对于大多数的节点分类任务,有一个预测函数:
GCN的灵感主要来自深度学习社区的CNN,它同时继承了非线性性质和特征变换性质,有研究致力于简化GCNs,例如SGC,它移除了非线性变换:
SGC最后可以表示为:
![]()
在SGC结构中,GCNs降低成了迭代的特征变换,只有很少的参数量。因此,模型可以用在大的数据集中,在调查中已经被证明,SGCN相当于在频域图中的一个低通滤波器,同时,实验表明SGCN不会对下游任务产生很大的负面影响。
基于图卷积的推荐
在本文中,我们主要关注基于隐式反馈的CF。在用户-物品的交互矩阵中,学习用户-物品的嵌入是推荐系统模型表现的关键。
带着GCNs的巨大成功,许多GCNs方法应用在推荐中,早期的工作主要在图的谱理论中,但是在真实世界中计算代价很大。最近的模型主要应用在空间域中,用户-物品二部图可以表示为:
然后,GCN迭代地应用等式1的嵌入传播和等式2的非线性变换,用户和物品的嵌入表示将会在嵌入过程中不断更新。因此,最后的嵌入表示![]() 将会表示在用户-物品之间的k阶连通性。
将会表示在用户-物品之间的k阶连通性。
深层网络体系结构设计
理论上说,深度神经网络可以近似表示任意函数。但是很多研究表明堆叠过多的层数会导致模型表现下降。研究表明深层的模型导致模型表现下降的原因不是过拟合,而是由于训练过程复杂导致训练损失过大。在基于CF的推荐系统中,由于数据稀疏性简单的神经网络表现都不会很好。因此,很多基于CF的模型都有两部分组成:浅宽部分和深神经网络部分。我们的模型基于GCN的线性结构,我们的结构关系如何使用残差结构来更好的保存先前的层。
线性残差图卷积协同过滤
拟议模型的总体结构
在本节中,我们提出了Linear Residual Graph Convolutional Collaborative Filtering(LR-GCCF)。
LR-GCCF相较于现有的GCNs结构有两个优点:1.在每一层的特征传播的时候,是使用简单的特征传播而不是非线性变换 2.为了预测用户对物品的喜好,我们使用了残差连接。
线性嵌入传播
![]() 代表着用户、物品的嵌入表示,LR-GCCF采用嵌入矩阵作为输入:
代表着用户、物品的嵌入表示,LR-GCCF采用嵌入矩阵作为输入:
![]()
和把节点特征当成输入的基于GCN的任务不同,这里的嵌入矩阵是不知道的且需要被训练。
线性嵌入传播过程:
对于单个用户或者物品来说(非矩阵形式):
![]() (
(![]() )是物品i(用户u)在图G中的对角度。
)是物品i(用户u)在图G中的对角度。![]() 是节点*的邻居。
是节点*的邻居。
残差偏好预测
在k层之后,输出为![]() 。对于每一个用户(物品),
。对于每一个用户(物品),![]() (
(![]() )获取了K阶二部图的相似性。很多基于CF的模型将会预测分数:
)获取了K阶二部图的相似性。很多基于CF的模型将会预测分数:
<,>表示点积。
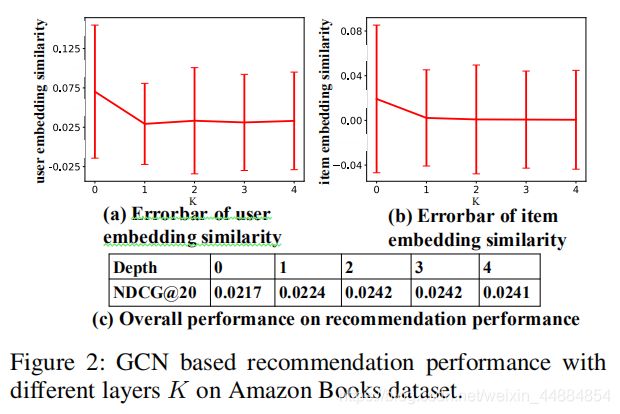
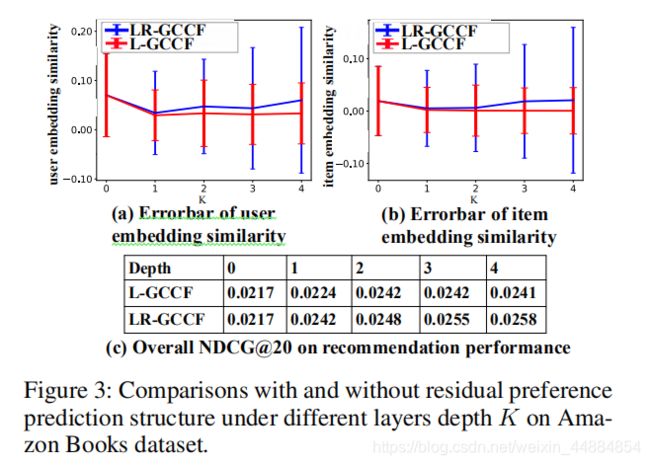
实际上,很多基于GCNs的变体达到最佳性能时模型的层数都是2。大致的趋势:随着k从0到1(2),模型表现会更好,但是如果再增大,模型的性能就是有很大降低。我们推测这种线性的原因:在第k层,每个节点都被k阶邻居平滑了。因此,随着层数从0到k,深层的嵌入表示变得过平滑了,每个节点都十分相似。这个问题不仅存在于GCN中,并且在数据稀疏的CF问题中尤其严重。为了验证我们的猜想,我们做了实验:
通过图中我们可以得出下面结论:
1.随着k的增加,由于k阶邻居的平滑,在用户(物品)之间的方差逐渐变小。
2.当k=0的时候,推荐模型的表现就已经很好了。当我们把从0增加到2,模型的性能增加小于10%。因此,我们从经验上得出结论:BPR(K=0)已经可以在很大程度上近似用户的偏好。
基于上面的观察,我们提出残差偏好学习:
我们假设优化残差rating比优化原始rating更简单,并且残差学习可以帮助缓解深层模型的过平滑现象。
最后我们的预测可以表示为:
这样做可以使得最后一层的模型表现更加丰富。
![]() ,
,![]() 表示
表示![]() 的
的![]() 次方。
次方。
由于我们基于隐式反馈,我们采用BPR中基于成对排序的损失函数为:
![]() 是sigmoid方程,
是sigmoid方程,![]() ,
,![]() ,
,![]() ,
,![]() 是正则化超参数。
是正则化超参数。
模型讨论
模型的深入分析
由等式14可以知道,LC-RCCF表示一个很深的模型,但是是一个宽的线性模型。线性特征含有以下几个好处:1.LR-GCCF基于SGC模型,理论证明了这和一个低通过滤波器的效果一样。2.有了线性嵌入传播和残差偏好学习,LR-GCCF相比于其他的非线性GCNs模型更容易训练。3.我们的模型相比于深度学习模型没有任何的隐藏层,我们不需要反向传播算法。与之相反,我们采用随机梯度下降法来训练模型。因此,LR-GCCF相比于标准的GCN模型更具有时间效率。
与先前工作的联系
我们对比了主要的集中基于GCNs的模型:
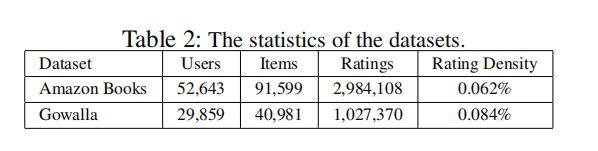
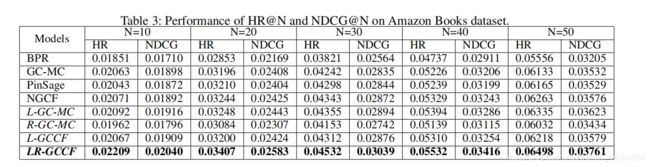
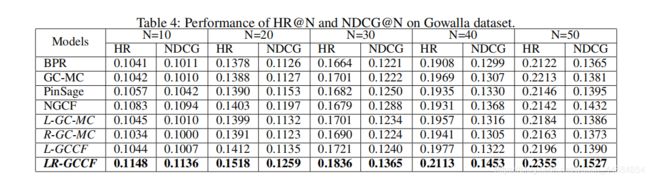
实验
结论:
在本文中,我们回顾了基于GCNs的推荐模型,并且提出了一种新的GCNs模型LR-GCCF。LR-GCCF主要有两点不同1.随着GCNs的见哈,我们的模型移除了GCNs的非线性变换,并且使用线性嵌入传播替代它。2.为了减低高层图卷积造成的过平滑现象,我们在每一层设计了一个残差表示学习块。多项实验证明了我们模型的有效性和高效性。在未来,我们探索如何整合不同的层表示来增强模型性能。