树状数组详解

1.树状数组

树状数组能够高效处理【对一个数组不断修改并求其前缀和】的问题，其修改与查询操作的复杂度都是 $O(\log n)$

1.1.定义

对于已经维护好的前缀和，如果需要修改，则需要付出 $O(n)$ 的代价

• 比如更改数组中的一个数，则其之后的前缀和的值都需要进行修改

树状数组是一种维护前缀和的数据结构，可以实现 $O(\log n)$查询一个前缀的和，$O(\log n)$ 对原数列的一个位置进行修改。

• 与前缀和相同的是，树状数组使用与原数列大小相同的数组即可维护

• 与前缀和不同的是，树状数组的一个位置 i 存储的是从 i 开始，（包括 i）向前 $t_i$ 个元素的和

  • $t_i$ 就是最大的可以整除 i 的2的幂（$2^0,2^1,2^2$等）
    

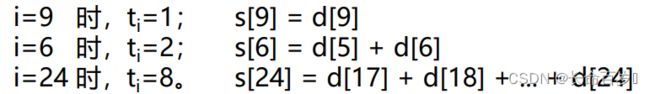
  • 将这些数转化成 2 进制更容易看出规律

    

  • 因为所有的整数都可以写成二进制形式，比如写成 $x=2^9+2^5+2^3$。我们找最大的可以整除 x 的2的幂，需要保证该数能够整除 $2^9,2^5,2^3$ 中的每一个，因此，这个数一定是这些相加的2的幂中最小的一个。$t_i$ 其实就是其二进制最低位的1，与其后的 0 组成的二进制数

1.2.lowbit(i)

从名字上，可以看出是用来找最低位的，也就是二进制最低位的 1 及其后面的 0 组成的数的十进制大小。

我们发现，找一个数二进制的最低位的1及其后的 0，可以通过如下方式来寻找

lowbit(i) = i & i 取反再 + 1

在计算机中，我们将负数，用其正数的补码（取反再加 1）形式来存储。这样的优点是利于计算机实现运算操作。

因此上面的式子可以写成 lowbit(i) = i & (-i)

1.3.树状数组的查询

对于指定位置 x，要查询 [1, x] 的前缀和。我们发现，区间 [1, x] 可以使用一些现有的区间来表示

• 对于区间 [1, 11] ，可以使用 s[11] + s[10] + s[8] 来表示

我们定义树状数组为 s。

对于一个 x，$S[x]={\sum }_{i\in \left(x-t_x,x\right]}d[i]$，若令 $y=x-t_x$，那么前一个紧邻的区间就可以使用 $(y-t_y,y]$ 来表示。就是 $S[y]$。这样不断迭代，就能完整的表示 [1, x] 区间

由于每次执行 $x-t_x$ 的操作都会使现在数字 2 进制中的 1 的数量减少 1（从低位向高维减少），因此，最坏情况下需要执行此操作 ${\log }_{2}x$，所以时间复杂度为 $O(\log n)$。

代码实现，查询的结果就是前缀和

int s[MAXN]
#define lb(x) (x & (-x))
int ask(int x){
    int res = 0;
    for(int i = x; i >= 1; i -= lb(i))
        res += s[i];
    return res;
}

如果需要查询一段区间 [l, r] 的和，使用 ask(r) - ask(l - 1)

1.4.树状数组的修改

对于指定位置 x，要将 d[x] 的值增加 v，只需要关心树状数组中哪些位置包含 d[x] 的值，依次进行修改即可

例如：把 d[5] 的值增加 v，则受到影响的点为 s[5], s[6], s[8] 等

树状数组的性质：

• 若当前节点为 x，且令 $x+t_x$ 为其父节点，则树状数组将形成一个树形结构

• 节点 x 记录区间 $(x-t_x,x]$ 的信息，其子节点记录的区间是 x 记录区间的子集，且子集之间不会相互覆盖

• 节点 x 记录的区间为节点 y 记录区间的子集，当且仅当 y 是 节点 x 的祖先节点

  

我们只需要访问 x 所有祖先节点即可

int s[MAXN], n;
#define lb(x) (x & (-x))
void upd(int x, int v){
    for(int i = x; i <= n; i += lb(i))
        s[i] += v;
}

2.逆序对问题

找逆序对（ $a_i>a_j$ 且 $i<j$ 的有序对）的个数，注意序列中可能有重复的数字

2.1.输入格式

第一行，一个数 n，表示序列中有 n 个数。

第二行 n 个数，表示给定的序列。序列中每个数字不超过 $10^9$。

2.2.输出格式

输出序列中逆序对的数目。

2.3.说明/提示

对于 $25\%$ 的数据，$n\le 2500$

对于 $50\%$ 的数据，$n\le 4\times 10^4。$

对于所有数据，$n\le 5\times 10^5$

2.4.思想

核心思想：假定问题数组为 a，我们从左向右遍历整个数组，当遍历到 a[i] 时

• 将其加入到树状数组中，也就是执行 upd(a[i], 1) 的操作。
• 然后查询 a[i] 作为逆序对中较大的那个数时，产生的逆序对的数量 i - ask(a[i])
  • 因为从左往右遍历，所以在前面的数，都会先进入树状数组中。ask(a[i])得到的值就是索引在前面，且小于等于 a[i] 的数的个数（每次加入比a[i]小的，都会使树状数组中a[i] 对应的值也增加 1）。i - ask(a[i]) 就是索引在前面，且比 a[i] 大的数的个数
• 如果，数的个数比较少，但是数的范围比较大，我们为了节省内存，需要进行离散化操作
  • 比如 n < 5000,a[i] < 10^9
  • 我们没法按数组中数原本的大小，开一个 $10^9$ 的数组，我们关注的是大小关系，只需要知道一个数是第几大的就行了，而不用关注其真实值到底是多少
    • 如果有相同大小的数，我们需要保证出现在前面的数，其新数（第几大），小于等于后出现数的新数，否则会将两个相同的数当做逆序对。这可以通过先对 a[i] 排序，再对索引排序来实现

2.5.代码

#include
using namespace std;
#define lb(x) (x & -x)
#define ll long long
int n;
int t[500005]; // 树状数组
int ranks[500005]; // 记录当前数是第几大的，相同的数会对应不同rank，只要保证先出现的 rank 小于后出现的就可以
ll tot = 0; // 逆序对数目

struct point{
    int val; // 记录值
    int index; // 记录在原数组中的索引
    bool operator < (point a) const{ // 先通过值排序,再通过索引排序
        if(a.val == val)
            return index < a.index;
        return val < a.val;
    }
};
point a[500005];

void upd(int x, int v){
    for(int i = x; i <= n; i += lb(i))
        t[i] += v;
}

ll ask(int x){
    ll sum = 0;
    for(int i = x; i >= 1; i -= lb(i))
        sum += t[i];
    return sum;
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        scanf("%d", &a[i].val);
        a[i].index = i;
    }
    sort(a + 1, a + 1 + n);
    for(int i = 1; i <= n; i++) // 遍历新数组
        ranks[a[i].index] = i; // 第 i 大的数是原数组中第 a[i].index 个数
    for(int i = 1; i <= n; i++){ // 遍历原数组
        upd(ranks[i], 1);
        tot += (i - ask(ranks[i]));
    }
    printf("%lld", tot);
}