蓝桥杯精选赛题算法系列——三体攻击——前缀和的逆运算

已收录此专栏。
前一讲讲解了前缀和的应用，这一将我们来看一下前缀和的逆运算——差分。

差分是一种处理数据的巧妙而简单的方法，它应用于区间的修改和询问问题。把给定的数据元素集 A 分成很多区间，对这些区间做很多次操作，每次操作是对某个区间内的所有元素做相同的加减操作，若一个个地修改这个区间内的每个元素，非常耗时。 引入“差分数组”D，当修改某个区间时，只需要修改这个区间的“端点”，就能记录整个区间的修改，而对端点的修改非常容易，是 O(1) 复杂度的。当所有的修改操作结束后，再利用差分数组，计算出新的 A。

上文描述的数据 A​ 可以是一维的线性数组 a[]​、二维矩阵 a[][]​、三维立体 ]a[][][]​。相应地，定义差分数组 D[]​、D[][]、D[][][]。一维差分很容易理解，二维和三维则需要一点想象力。

让我们来考虑这么一个场景：

1. 给定一个长度为 n 的一维数组a[]，数组内每个元素有初始值。 修改操作：做 m
2. 次区间修改，每次修改对区间内所有元素做相同的加减操作。例如第 i 次修改，把区间[Li,Ri] 内所有元素加上 di。
   3.询问操作：询问一个元素的新值是多少。

在差分法中，我们需要用到两个数组：原数组 a[]、差分数组 D[]。
D[] 的定义是 D[k] = a[k] - a[k-1]，即原数组a[]的相邻元素的差。从定义可以推出 a[k] = D[1] + D[2] + … + D[k] =，也就是说，a[] 是 D[] 的前缀和。这个公式揭示了a[] 和 D[]的关系。差分把求 a[k]转化为求 D 的前缀和。
为加深对前缀和的理解，可以把每个 D[] 看成一条直线上的小线段，它的两端是相邻的 a[]；这些小线段相加，就得到了从起点开始的长线段 a[]​。
如图，把每个 D[] 看成小线段，把每个 a[] 看成从 a[1] 开始的小线段的和

注意， a[] 和 D[] 的值都可能为负，上面图中所有的 D[]​ 都是长度为正的线段，只是为了方便图示。

如何用差分数组记录区间修改？为什么利用差分数组能提升修改的效率呢？
我么来进行一遍演示：
把区间 [L, R] 内每个元素 a[] 加上 d，只需要把对应的 D[] 做以下操作：
把 D[L] 加上 d： D[L] += d
把 D[R+1]减去 d：D[R + 1] -= d
利用 D[]，能精确地实现只修改区间内元素的目的，而不会修改区间外的a[] 值。因为前缀和 a[x] = D[1] + D[2] + … + D[x]，有：
1≤x L≤x≤R，前缀和 a[x] 增加了d；
R 所以每次操作只需要修改区间 [L, R] 的两个端点的D[] 值。

接下来看一道题，这个题有一定的难度，我也是直接看的答案嘿嘿，有能力的可以自己做一做。

题目描述

三体人将对地球发起攻击。为了抵御攻击，地球人派出A × B × C 艘战舰，在太空中排成一个 A 层 B 行 C 列的立方体。其中，第 i 层第 j 行第 k 列的战舰（记为战舰 (i, j, k)）的生命值为d(i, j, k)。

三体人将会对地球发起 m 轮"立方体攻击"，每次攻击会对一个小立方体中的所有战舰都造成相同的伤害。具体地，第 t 轮攻击用 7 个参数 lat, rat, lbt, rbt, lct, rct, ht 描述；

所有满足 i ∈ [lat, rat],j ∈ [lbt, rbt],k ∈ [lct, rct]的战舰 (i, j, k)会受到 ht 的伤害。如果一个战舰累计受到的总伤害超过其防御力，那么这个战舰会爆炸。

地球指挥官希望你能告诉他，第一艘爆炸的战舰是在哪一轮攻击后爆炸的。

输入描述
第一行包括 4 个正整数 A, B, C, m；

第二行包含 A × B × C 个整数，其中第 ((i − 1)×B + (j − 1)) × C + (k − 1)+1 个数为 d(i, j, k)；

第 3 到第 m + 2 行中，第 (t − 2) 行包含 7 个正整数 lat, rat, lbt, rbt, lct, rct, ht。

其中,A × B × C ≤ 10⁶, m ≤ 10⁶ , 0 ≤ d(i, j, k), ht ≤ 10⁹ 。

输出描述

输出第一个爆炸的战舰是在哪一轮攻击后爆炸的。保证一定存在这样的战舰。

样例输入

2 2 2 3
1 1 1 1 1 1 1 1
1 2 1 2 1 1 1
1 1 1 2 1 2 1
1 1 1 1 1 1 2

样例输出

2

解题方法

这个题用了三维差分，这个我感觉题非常难，所以……唉，本人能力有限，只能用暴力法解这个题，下面是我的源码：

A,B,C,m = map(int,input().split())
a = list(map(int,input().split()))
wzy = [[[0 for _ in range(A)] for _ in range(B) ]for _ in range(C)]
for i in range(1,A+1):
    for j in range(1,B+1):
        for k in range(1,C+1):
            wzyan = ((i-1)*B+(j-1))*C+(k-1)+1
            wzy[i-1][j-1][k-1] = a[wzyan-1]

for z in range(1,m+1):
    lat,rat,lbt,rbt,lct,rct,ht = map(int,input().split())
    for  i in range(1,A+1):
        for j in range(1,B+1):
            for k in range(1,C+1):
                if i>=lat and i<=rat and j>=lbt and j<=rbt and k>=lct and k<=rct:
                    wzy[i-1][j-1][k-1] -=ht
                if wzy[i-1][j-1][k-1] < 0:
                    print(z)
                    exit()

但是这个题这种解法肯定是最笨的，正确解法应该就是用我们这一节的方法——差分法，接下来，就让我们了解一下一维差分，二维差分，三维差分的解题思路。

一维差分讲解

一维，即所有战舰排成一条线，每次把一个区间内的所有元素（战舰生命值）减去一个相同的 ht 值。这是经典的“一维区间修改问题”，可以用“差分数组”来处理数据。 但是光用差分数组不够，还是不能解决问题。因为在差分数组上查询区间内的每个元素是否小于 0，需要用差分数组来计算区间内每个元素的值。也是非常的复杂，那该怎么办呢？
这就要加上第二个算法：二分法。
从第 1次修改到第 m 次修改，肯定有一次修改是临界点。在这次修改前，没有负值（战舰爆炸）；在这次修改后，出现了负值，且后面一直有负值。那么对 m 进行二分，具体的操作步骤如下：

1.读取输入：存储 n=A × B × C 个点（战舰）的生命值；存储 m 次修改。
2.第 1 次二分，从最大的 m 开始：判断做 m 次修改后是否产生负值。过程是：先做 m 次差分修改，得到一个差分数组；然后根据这个差分数组计算每个战舰的值，看是否有负数。
3.重复以上二分操作，直到找到临界修改的次数。

二维差分讲解

我们从一维差分扩展到二维差分比较容易。一维是线性数组，一个区间[L,R]有两个端点；二维是矩阵，一个区间由四个端点围成。下面从一维差分推广到二维差分。
前缀和
还记得在一维差分中 a[]的含义吧。
在一维差分中，原数组 a[]​ 是从第 1​ 个 D[1]​ 开始的差分数组 D[]​ 的前缀和：a[k]=D[1]+D[2]+⋯+D[k]​。
而在二维差分中，a[][] 是差分数组 D[][] 的前缀和，即由原点坐标 (1,1) 和坐标 (i,j) 围成的矩阵中，所有的 D[][] 相加等于 a[i][j]。为加深对前缀和的理解，我们可以把每个 D[][] 看成一个小格；在坐标(1,1) 和 (i,j) 所围成的范围内，所有小格子加起来的总面积，就等于 a[i][j]。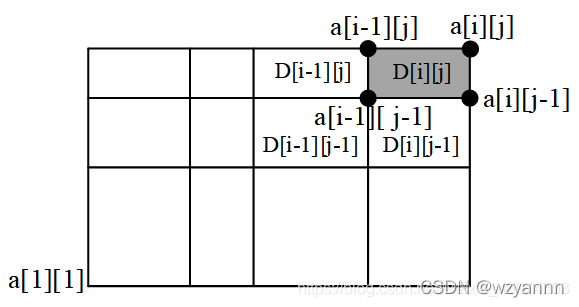
上面的图中，每个格子的面积是一个 D[][]，例如阴影格子是 D[i][j]，它由 4 个坐标点定义：(i−1,j)、(i,j)、(i−1,j−1)、(i,j−1)。坐标点 (i,j) 的值是 a[i][j]，它等于坐标(1,1) 和 (i,j)​ 所围成的所有格子的总面积。图中故意把小格子画得长宽不同，是为了体现它们的面积不同。
根据上述，我们来给出二维差分的定义。在一维情况下，D[i]=a[i]−a[i−1]。在二维情况下，差分变成了相邻的 a[][] 的“面积差”，计算公式是：D[i][j]=a[i][j]–a[i−1][j]–a[i][j−1]+a[i−1][j−1]。这个公式可以通过上面的图来观察。阴影方格表示 D[i][j]D[i][j] 的值，它的面积这样求：大面积 a[i][j] 减去两个小面积 a[i−1][j]、a[i][j−1]，由于两个小面积的公共面积 a[i−1][j−1] 被减了 2 次，所以需要加回来 1 次。
那二维差分的区间修改该如何处理呢？
在一维情况下，做区间修改只需要修改区间的两个端点的 D[] 值。而在二维情况下，一个区间是一个小矩阵，有 4 个端点，只需要修改这 4 个端点的 D[][]值。例如坐标点(x1,y1)∼(x2,y2)定义的区间，对应4个端点的D[][]：

D[x1][y1]     += d;     //二维区间的起点
D[x1][y2+1]   -= d;     //把x看成常数，y从y1到y2+1
D[x2+1][y1]   -= d;     //把y看成常数，x从x1到x2+1
D[x2+1][y2+1] += d;     //由于前两式把d减了2次，多减了1次，这里加1次回来

下图是区间修改的图示。2 个黑色点围成的矩形是题目给出的区间修改范围。我们只需要改变 4个 D[][] 值，即改变图中的 4​ 个阴影块的面积即可。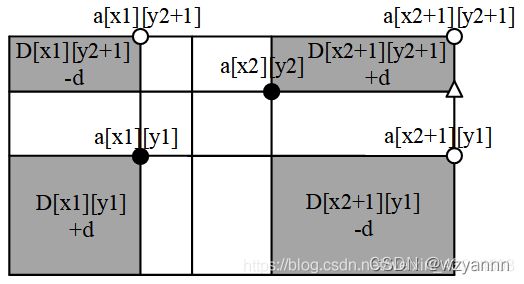
你可以用这个图，观察每个坐标点的 a[][]值的变化情况。例如符号“∆”标记的坐标(x2+1,y2)，它在修改的区间之外；a[x2+1][y2] 的值是从(1,1) 到 (x2+1,y2) 的总面积，在这个范围内，D[x1][y1]+d，D[x2+1][y1]−d，两个 d 抵消，a[x2+1][y2]保持不变。

前缀和 a[][] 的计算用到了递推公式：a[i][j]=D[i][j]+a[i−1][j]+a[i][j−1]−a[i−1][j−1]。

三维差分讲解

三维差分的模板代码比较少见。三维差分比较复杂，请结合本节中的几何图进行理解。

与一维差分、二维差分的思路类似，下面给出三维差分的有关特性：

1.元素的值用三维数组 a[][][] 来定义，差分数组D[][][] 也是三维的。把三维差分想象成在立体空间上的操作。一维的区间是一个线段，二维是矩形，那么三维就是立体块。一个小立体块有 8 个顶点，所以三维的区间修改，需要修改 8个D[][][]​ 值。

2.前缀和。
在二维差分中，a[][] 是差分数组 D[][] 的前缀和，即由原点坐标 (1,1) 和坐标 (i,j) 围成的矩阵中，所有的 D[][]（看成小格子）相加等于a[i][j]（看成总面积）。
而在三维差分中，a[][][] 是差分数组 D[][][] 的前缀和。即由原点坐标(1,1,1) 和坐标(i,j,k) 所标记的范围中，所有的 D[][][] 相加等于a[i][j][k]。我们同样把每个 D[][][] 看成一个小立方体；在坐标 (1,1,1) 和(i,j,k) 所围成的空间中，所有小立体块加起来的总体积，等于 a[i][j][k]。每个小立方体由 8 个坐标点定义，见下面图中的坐标点。坐标点 (i,j,k) 的值是 a[i][j][k]；D[i][j][k] 的值是图中小立方体的体积。

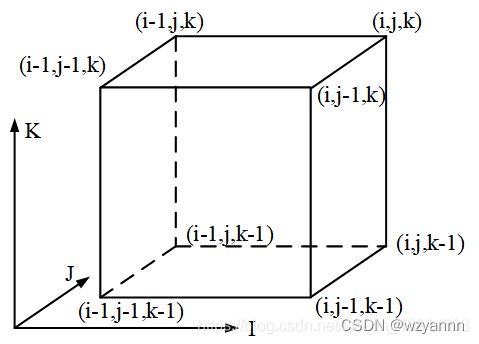
3.差分的定义。 在三维情况下，差分变成了相邻的 a[][][] 的“体积差”。如何写出差分的递推计算公式呢？ 一维差分和二维差分的递推计算公式很好写。三维差分，D[i][j][k] 的几何意义是图中小立方体的体积，它可以通过这个小立方体的 8 个顶点的值推出来。思路与二维情况下类似，二维的 D[][] 是通过小矩形的四个顶点的 a[][] 值来计算的。不过，三维情况下，递推计算公式很难写，8 个顶点有 8 个a[][][]，把脑袋绕晕了也不容易写对。

4.区间修改。在三维情况下，一个区间是一个立方体，有 8 个顶点，只需要修改这 8 个顶点的 D[][][] 值。例如坐标点 (x1,y1,z1)∼(x2,y2,z2) 定义的区间，对应 8 个 D[][][]，请对照上面的图来想象它们的位置。

D[x1][y1][z1]       += d;   //前面：左下顶点，即区间的起始点
D[x2+1][y1][z1]     -= d;   //前面：右下顶点的右边一个点
D[x1][y1][z2+1]     -= d;   //前面：左上顶点的上面一个点
D[x2+1][y1][z2+1]   += d;   //前面：右上顶点的斜右上方一个点
D[x1][y2+1][z1]     -= d;   //后面：左下顶点的后面一个点
D[x2+1][y2+1][z1]   += d;   //后面：右下顶点的斜右后方一个点
D[x1][y2+1][z2+1]   += d;   //后面：左上顶点的斜后上方一个点
D[x2+1][y2+1][z2+1] -= d;   //后面：右上顶点的斜右上后方一个点，即区间终点的后一个点

下面给出大佬用三维差分对上面那道三体攻击题的代码，大佬终究是大佬！

//good.cpp
#include
int A,B,C,n,m;
const int Maxn = 1000005;
int s[Maxn];   //存储舰队生命值
int D[Maxn];   //三维差分数组（压维）；同时也用来计算每个点的攻击值
int x2[Maxn], y2[Maxn], z2[Maxn]; //存储区间修改的范围，即攻击的范围
int x1[Maxn], y1[Maxn], z1[Maxn]; 

int d[Maxn];                    //记录伤害，就是区间修改
int num(int x,int y,int z) {  
//小技巧：压维，把三维坐标[(x,y,z)转为一维的((x-1)*B+(y-1))*C+(z-1)+1
    if (x>A || y>B || z>C) return 0;
    return ((x-1)*B+(y-1))*C+(z-1)+1;
}
bool check(int x){ //做x次区间修改。即检查经过x次攻击后是否有战舰爆炸
    for (int i=1; i<=n; i++)  D[i]=0;  //差分数组的初值，本题是0
    for (int i=1; i<=x; i++) {  //用三维差分数组记录区间修改：有8个区间端点
        D[num(x1[i],  y1[i],  z1[i])]   += d[i];
        D[num(x2[i]+1,y1[i],  z1[i])]   -= d[i];
        D[num(x1[i],  y1[i],  z2[i]+1)] -= d[i];
        D[num(x2[i]+1,y1[i],  z2[i]+1)] += d[i];
        D[num(x1[i],  y2[i]+1,z1[i])]   -= d[i];
        D[num(x2[i]+1,y2[i]+1,z1[i])]   += d[i];
        D[num(x1[i],  y2[i]+1,z2[i]+1)] += d[i];
        D[num(x2[i]+1,y2[i]+1,z2[i]+1)] -= d[i];
    }
    //下面从x、y、z三个方向计算前缀和
    for (int i=1; i<=A; i++)
        for (int j=1; j<=B; j++)
            for (int k=1; k<C; k++)  //把x、y看成定值，累加z方向
                D[num(i,j,k+1)] += D[num(i,j,k)];
    for (int i=1; i<=A; i++)
        for (int k=1; k<=C; k++)
            for (int j=1; j<B; j++)   //把x、z看成定值，累加y方向
                D[num(i,j+1,k)] += D[num(i,j,k)];
    for (int j=1; j<=B; j++)
        for (int k=1; k<=C; k++)
            for (int i=1; i<A; i++)   //把y、z看成定值，累加x方向
                D[num(i+1,j,k)] += D[num(i,j,k)];
    for (int i=1; i<=n; i++)    //最后判断是否攻击值大于生命值
        if (D[i]>s[i])
            return true;
    return false;
}
int main() {
    scanf("%d%d%d%d", &A, &B, &C, &m);
    n = A*B*C;
    for (int i=1; i<=n; i++) scanf("%d", &s[i]);  //读生命值
    for (int i=1; i<=m; i++)    //读每次攻击的范围，用坐标表示
scanf("%d%d%d%d%d%d%d",&x1[i],&x2[i],&y1[i],&y2[i],&z1[i],&z2[i],&d[i]);

    int L = 1,R = m;      //经典的二分写法
    while (L<R) {     //对m进行二分，找到临界值。总共只循环了log(m)次
        int mid = (L+R)>>1;
        if (check(mid)) R = mid;
        else L = mid+1;
    }
    printf("%d\n", R);  //打印临界值
    return 0;
}

其中 check() 函数包含了三维差分的全部内容。代码有几个关键点：

1.没有定义a[][][]，而是用D[][][] 来代替。

2.压维。 直接定义三维差分数组 D[][][] 不太方便。虽然坐标点总数量n=A×B×C=10⁶比较小，但是每一维都需要定义到 10⁶,那么总空间就是 10¹⁸ 。为避免这一问题，可以把三维坐标压维成一维数组 D[]，总长度仍然是 10⁶ 的。这个技巧很有用。实现函数是 num()，它把三维坐标 (x,y,z)(x,y,z) 变换为一维坐标

h=(x−1)×B×C+(y−1)×C+(z−1)+1

当 x、y、z 的取值范围分别是 1∼A、1∼B、1∼C 时，h 的范围是1∼A×B×C。

如果希望按 C 语言的习惯从 0​ 开始，x​、y​、z​ 的取值范围分别是 0∼A−1​、0∼B−1​、0∼C−1​，h​ 范围是
0∼A×B×C−1​，就把式子改为：h=x×B×C+y×C+z。 同理，二维坐标 (x,y)​ 也可以压维成一维
h=(x−1)×B+(y−1)+1 当 x、y 的取值范围分别是1∼A、1∼B 时，h的范围是 1∼A×B。

check() 中 19−26 行，在 D[] 上记录区间修改。

check() 中29−40 行的 3 个 for 循环计算前缀和，原理见二维差分的代码。它分别从 x、y、z​ 三个方向累加小立方体的体积，计算出所有的前缀和。