《算法笔记》学习日记——9.5 平衡二叉树（AVL）&9.6 并查集

9.5 平衡二叉树（AVL）

Codeup Contest ID:100000614

问题 A: 算法9-9~9-12：平衡二叉树的基本操作

题目描述
平衡二叉树又称AVL树，它是一种具有平衡因子的特殊二叉排序树。平衡二叉树或者是一棵空树，或者是具有以下几条性质的二叉树：

1. 若它的左子树不空，则左子树上所有结点的值均小于它的根节点的值；
2. 若它的右子树不空，则右子树上所有结点的值均大于它的根节点的值；
3. 它的左右子树也分别为平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。

若将二叉树上结点的平衡因子定义为该结点的左子树深度减去它的右子树的深度，则平衡二叉树上的所有结点的平衡因子只可能为-1、0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1，则这棵二叉树就是不平衡的。
通过平衡二叉树的性质不难得知，其插入、删除、查询都操作的时间复杂度均为O(log2n)。
维持平衡二叉树性质的操作可以被称为旋转。其中平衡二叉树的右旋处理可以描述如下：

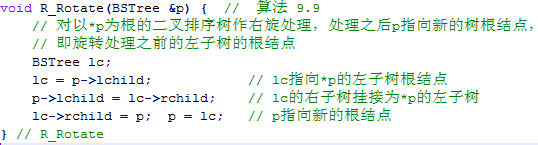
而其左旋处理与右旋正好相反，可以描述如下：

在本题中，读入一串整数，首先利用这些整数构造一棵平衡二叉树。另外给定多次查询，利用构造出的平衡二叉树，判断每一次查询是否成功。
输入
输入的第一行包含2个正整数n和k，分别表示共有n个整数和k次查询。其中n不超过500，k同样不超过500。
第二行包含n个用空格隔开的正整数，表示n个整数。
第三行包含k个用空格隔开的正整数，表示k次查询的目标。
输出
只有1行，包含k个整数，分别表示每一次的查询结果。如果在查询中找到了对应的整数，则输出1，否则输出0。
请在每个整数后输出一个空格，并请注意行尾输出换行。
样例输入

8 3
1 3 5 7 8 9 10 15
9 2 5

样例输出

1 0 1 

提示
在本题中，首先需要按照题目描述中的算法完成平衡二叉树的构造过程，之后需要通过在平衡二叉树中的不断向下查找，将需要查询的值与当前节点的值进行比较，直到确定被查询的值是否存在。
通过课本中的性能分析部分，不难发现平衡二叉树的查找、插入、删除等操作的时间复杂度均为O(log2n)，这是通过利用旋转操作使二叉树保持平衡状态而保证的。
思路
这题总的思路还是比较简单的，就是把读入的数据存储起来，然后建AVL树，建完之后再依次对要查询的数据进行查询就好了。
唯一的难点就是AVL树的各种操作内置的函数多了点，尽量靠自己的理解写吧。
代码

#include
#include
#include
#include
#include
#include
using namespace std;
const int maxn = 501;
struct node{
	int data;
	int height;//AVL树不要忘了记录当前结点的树高 
	node* lchild;
	node* rchild;
};
int Data[maxn] = {0};//存储AVL树的结点数据 
node* newNode(int x){
	node* Node = new node;
	Node->data = x;
	Node->height = 1;//初始化为1 
	Node->lchild = Node->rchild = NULL;
	return Node;
}
int getHeight(node* root){
	if(root==NULL) return 0;//空树返回的是0,不是1 
	return root->height;
}
int getBalanceFactor(node* root){
	return getHeight(root->lchild)-getHeight(root->rchild);
}
void updateHeight(node* root){
	root->height = max(getHeight(root->lchild), getHeight(root->rchild))+1;
}
void L(node* &root){
	node* temp = root->rchild;
	root->rchild = temp->lchild;
	temp->lchild = root;
	updateHeight(root);
	updateHeight(temp);
	root = temp;
}
void R(node* &root){
	node* temp = root->lchild;
	root->lchild = temp->rchild;
	temp->rchild = root;
	updateHeight(root);
	updateHeight(temp);
	root = temp;
}
void Search(node* root, int x){
	if(root==NULL){
		printf("0 ");//查找失败
		return;//查找之后记得return掉 
	}
	if(root->data==x){
		printf("1 ");//查找成功 
		return;//查找之后记得return掉 
	}
	else if(x<root->data) Search(root->lchild, x);
	else Search(root->rchild, x);
}
void Insert(node* &root, int x){
	if(root==NULL){
		root = newNode(x);
		return;
	}
	if(x<root->data){
		Insert(root->lchild, x);
		updateHeight(root);
		if(getBalanceFactor(root)==2){
			if(getBalanceFactor(root->lchild)==1){//LL型 
				R(root);
			}
			if(getBalanceFactor(root->lchild)==-1){//LR型 
				L(root->lchild);
				R(root);
			}
		}
	}
	else{
		Insert(root->rchild, x);
		updateHeight(root);
		if(getBalanceFactor(root)==-2){
			if(getBalanceFactor(root->rchild)==-1){//RR型 
				L(root);
			}
			if(getBalanceFactor(root->rchild)==1){//RL型 
				R(root->rchild);
				L(root);
			}
		}
	}
}
node* Create(int data[], int n){
	node* root = NULL;
	for(int i=0;i<n;i++) Insert(root, data[i]);
	return root;
}
int main(){
	int n, k;
	while(scanf("%d%d", &n, &k) != EOF){
		for(int i=0;i<n;i++){
			scanf("%d", &Data[i]);//输入要处理的数据 
		}
		node* root = Create(Data, n);//建树
		for(int i=0;i<k;i++){
			int tmp;
			scanf("%d", &tmp);//输入要查找的数据 
			Search(root, tmp);
		}
		printf("\n");
		memset(Data, 0, sizeof(Data));
	}
	return 0;
}

小结

AVL树是一棵严格平衡的二叉查找树（红黑树不是严格平衡的），正因如此，它在插入时调整平衡的操作比较复杂（需要时刻动态地根据四种树型进行调整），但是旋转操作只有左旋和右旋两种，因此理解性地记忆的话，还是不算难的，不过代码量是真的偏多（捂脸）……

9.6 并查集

Codeup Contest ID:100000615

问题 A: 通信系统

题目描述
某市计划建设一个通信系统。按照规划，这个系统包含若干端点，这些端点由通信线缆链接。消息可以在任何一个端点产生，并且只能通过线缆传送。每个端点接收消息后会将消息传送到与其相连的端点，除了那个消息发送过来的端点。如果某个端点是产生消息的端点，那么消息将被传送到与其相连的每一个端点。
为了提高传送效率和节约资源，要求当消息在某个端点生成后，其余各个端点均能接收到消息，并且每个端点均不会重复收到消息。
现给你通信系统的描述，你能判断此系统是否符合以上要求吗？
输入
输入包含多组测试数据。每两组输入数据之间由空行分隔。
每组输入首先包含2个整数N和M，N（1<=N<=1000）表示端点个数，M（0<=M<=N*(N-1)/2）表示通信线路个数。
接下来M行每行输入2个整数A和B（1<=A，B<=N），表示端点A和B由一条通信线缆相连。两个端点之间至多由一条线缆直接相连，并且没有将某个端点与其自己相连的线缆。
当N和M都为0时，输入结束。
输出
对于每组输入，如果所给的系统描述符合题目要求，则输出Yes，否则输出No。
样例输入

4 3
1 2
2 3
3 4

3 1
2 3

0 0

样例输出

Yes
No

思路
这题也是一个经典的并查集题目，我个人感觉和书上的【好朋友】这道题几乎一模一样，同样的，每给一组点的信息，就对它们俩执行合并操作，最后计算有几个集合就行了，如果只有一个集合，说明所有端点之间都有线路，都能收到信息，如果不止一个集合，说明肯定有两个端点之间是不通的，也就是说传不到信息。
代码

#include
#include
#include
#include
#include
using namespace std;
const int maxn = 1010;
int father[maxn];
bool isRoot[maxn];
int findFather(int x){
	int a = x;
	while(x!=father[x]){
		x = father[x];
	}
	while(a!=father[a]){
		int z = a;
		a = father[a];
		father[z] = x;
	}
	return x;
}
void Union(int a, int b){
	int faA = findFather(a);
	int faB = findFather(b);
	if(faA!=faB){
		father[faA] = faB;
	}
}
int main(){
	int N, M;//N是端点个数,M是通信线路个数 
	while(scanf("%d%d", &N, &M) != EOF){
		if(N==0&&M==0) break;
		for(int i=0;i<maxn;i++) father[i] = i;//初始化并查集 
		for(int i=0;i<M;i++){
			int tmp1, tmp2;
			scanf("%d%d", &tmp1, &tmp2);
			Union(tmp1, tmp2);
		}
		int ans = 0;
		for(int i=1;i<=N;i++){
			isRoot[findFather(i)] = true;//把集合的根节点置true 
		}
		for(int i=1;i<=N;i++){
			if(isRoot[i]==true) ans++;
		}
		if(ans==1) printf("Yes\n");
		else printf("No\n");
	}
	return 0;
}

问题 B: 畅通工程

题目描述
某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？
输入
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时，输入结束，该用例不被处理。
输出
对每个测试用例，在1行里输出最少还需要建设的道路数目。
样例输入

5 3
1 2
3 2
4 5
0

样例输出

1

思路
这题也一样，感觉题目都在暗示这是个并查集了（不一定有直接的道路相连，只要互相间接通过道路可达即可），所以最少需要建设多少条道路就相当于问你是有几个集合（最少还要建设的道路数=集合数-1，比如样例给的明显是两个集合，为了把两个集合合并，因此还需要一条根结点和根结点之间的道路）。
这题一开始答案错误50了，原因是一次样例处理完之后没有清空isRoot数组（上题应该也要加这么一句话，但是没加居然AC了……）。
代码

#include
#include
#include
#include
#include
using namespace std;
const int maxn = 1010;
int father[maxn];
bool isRoot[maxn];
int findFather(int x){
	int a = x;
	while(x!=father[x]){
		x = father[x];
	}
	while(a!=father[a]){
		int z = a;
		a = father[a];
		father[z] = x;
	}
	return x;
}
void Union(int a, int b){
	int faA = findFather(a);
	int faB = findFather(b);
	if(faA!=faB){
		father[faA] = faB;
	}
}
int main(){
	int N;
	while(scanf("%d", &N) != EOF){
		if(N==0) break;
		int M;
		scanf("%d", &M);
		for(int i=0;i<maxn;i++){
			father[i] = i;//初始化 
		}
		for(int i=0;i<M;i++){
			int tmp1, tmp2;
			scanf("%d%d", &tmp1, &tmp2);
			Union(tmp1, tmp2);
		}
		for(int i=1;i<=N;i++){
			isRoot[findFather(i)] = true;
		}
		int ans = 0;
		for(int i=1;i<=N;i++){
			if(isRoot[i]==true) ans++;
		}
		printf("%d\n", ans-1);//集合数-1才是要建设的道路数
		memset(isRoot, 0, sizeof(isRoot));
	}
	return 0;
}

问题 C: How Many Tables

题目描述
Today is Ignatius’ birthday. He invites a lot of friends. Now it’s dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.
One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.
For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.
输入
The input starts with an integer T(1<=T<=25) which indicate the number of test cases. Then T test cases follow. Each test case starts with two integers N and M(1<=N,M<=1000). N indicates the number of friends, the friends are marked from 1 to N. Then M lines follow. Each line consists of two integers A and B(A!=B), that means friend A and friend B know each other. There will be a blank line between two cases.
输出
For each test case, just output how many tables Ignatius needs at least. Do NOT print any blanks.
样例输入

2
6 4
1 2
2 3
3 4
1 4

8 10
1 2
2 3
5 6
7 5
4 6
3 6
6 7
2 5
2 4
4 3

样例输出

3
2

思路
思路也很简单，因为题目说了如果A和B是朋友，B和C也是朋友的话，那么A和C也是朋友，于是这就是一个并查集的模型，同理，问多少张桌子其实就是问有几个集合。
代码

#include
#include
#include
#include
#include
using namespace std;
const int maxn = 1010;
int father[maxn];
bool isRoot[maxn];
int findFather(int x){
	int a = x;
	while(x!=father[x]){
		x = father[x];
	}
	while(a!=father[a]){
		int z = a;
		a = father[a];
		father[z] = x;
	}
	return x;
}
void Union(int a, int b){
	int faA = findFather(a);
	int faB = findFather(b);
	if(faA!=faB){
		father[faA] = faB;
	}
}
int main(){
	int T;
	while(scanf("%d", &T) != EOF){
		while(T--){
			int N, M;
			scanf("%d%d", &N, &M);
			for(int i=0;i<maxn;i++) father[i] = i;//初始化 
			for(int i=0;i<M;i++){
				int tmp1, tmp2;
				scanf("%d%d", &tmp1, &tmp2);
				Union(tmp1, tmp2);
			}
			for(int i=1;i<=N;i++){
				isRoot[findFather(i)] = true;
			}
			int ans = 0;
			for(int i=1;i<=N;i++){
				if(isRoot[i]==true) ans++;
			}
			printf("%d\n", ans);
			memset(isRoot, 0, sizeof(isRoot));
		}
	}
	return 0;
}

问题 D: More is better

题目描述
Mr Wang wants some boys to help him with a project. Because the project is rather complex, the more boys come, the better it will be. Of course there are certain requirements.Mr Wang selected a room big enough to hold the boys. The boy who are not been chosen has to leave the room immediately. There are 10000000 boys in the room numbered from 1 to 10000000 at the very beginning. After Mr Wang’s selection any two of them who are still in this room should be friends (direct or indirect), or there is only one boy left. Given all the direct friend-pairs, you should decide the best way.
输入
The first line of the input contains an integer n (0 ≤ n ≤ 100 000) - the number of direct friend-pairs. The following n lines each contains a pair of numbers A and B separated by a single space that suggests A and B are direct friends. (A ≠ B, 1 ≤ A, B ≤ 10000000)
输出
The output in one line contains exactly one integer equals to the maximum number of boys Mr Wang may keep.
样例输入

3
1 3
1 5
2 5
4
3 2
3 4
1 6
2 6

样例输出

4
5

思路
这题其实也很简单，但是又被自己的一个小错误坑了一个晚上，原因在于这题和前面的题稍有不同，前面的题都给出了每个样例的最大结点编号N，于是，处理isRoot数组的时候只需要从i=1循环到i=N就好了，但是这题不一样，这题给的n只是有n对朋友，但是至于这些人的编号具体到多大，就无从得知了。

但是总不能从i=1一直循环到i=10⁷吧，那样肯定会超时，所以必须得记录输入编号的最大值，其实这个最大值的判断呢是很简单的，只要设一个变量maxi，只要当前输入的数比它大，那么就更新maxi的值，然后我就犯了一个很蠢很蠢的错误，以至于买了题库还没发现错在哪（金币-1 o(╥﹏╥)o），直到后来某一次我试着把样例2倒过来输入，才发现我的maxi居然才到3（按理来说是应该是6），然后看了一下自己写的关于maxi的代码，才恍然大悟（真想打死那个时候的我，我本来最早的思路就是想用两个if语句更新maxi的值的，然后不知道为啥脑子抽了非要用max函数装个x，结果错了一晚上）。

思路还是最普通的并查集，只不过这一题要求的是集合的元素个数，书上也说了，如果要求集合的元素个数，那么只要把isRoot改为int型即可，因为该数组的下标代表着以此为根结点的一个集合，因此，只要对每个编号进行findFather()的操作，然后对应根结点的下标+1，这样处理完之后，isRoot数组里面存储的就是每个根结点对应的元素总数（因为根结点代表着一个集合，因此，也就是每个集合的元素总数），最后只要找这个数组里的最大值就是答案啦~
代码

#include
#include
#include
#include
#include
#include
using namespace std;
const int maxn = 10000001;
int father[maxn];
int isRoot[maxn] = {0};
int findFather(int x){
	int a = x;
	while(-1!=father[x]){//因为用了memset置根结点的父亲是-1,所以这里的判断条件也要改一下 
		x = father[x];
	}
	while(-1!=father[a]){
		int z = a;
		a = father[a];
		father[z] = x;
	}
	return x;
}
void Union(int a, int b){
	int faA = findFather(a);
	int faB = findFather(b);
	if(faA!=faB){
		father[faA] = faB;
	}
}
int main(){
	int n;
	while(scanf("%d", &n) != EOF){
		int maxi = 0; 
		if(n==0){
			printf("1\n");//特判输出只有1个人的情况
		}
		else{
			memset(father, -1, sizeof(father));//memset比for循环快一点,所以这里用了memset 	
			for(int i=0;i<n;i++){
				int tmp1, tmp2;
				scanf("%d%d", &tmp1, &tmp2);
				if(tmp1>maxi) maxi = tmp1;//更新maxi的值,这是为了记录最大的编号,以减少处理isRoot时的耗时
				if(tmp2>maxi) maxi = tmp2;
				//maxi = max(tmp1, tmp2);=>这个错误很蠢,这里只是取当前tmp1和tmp2的最大值,只要倒序输入maxi就会出错
				//maxi = max(max(tmp1, tmp2), maxi);=>这样就能实时更新maxi的值了 
				Union(tmp1, tmp2);
			}
			for(int i=1;i<=maxi;i++){//只要循环到maxi,如果循环到maxn肯定是会超时的 
				isRoot[findFather(i)] += 1;//i结点的根结点代表一个集合,因此直接+1就代表该集合的元素数量
			}
			int max = 1;
			for(int i=1;i<=maxi;i++){
				if(isRoot[i]>max) max = isRoot[i];//更新max的值
			} 
			printf("%d\n", max);
			memset(isRoot, 0, sizeof(isRoot));
		}
	}
	return 0;
}

小结

并查集总的来说还是比较简单的，因为总共只有两个操作：①查找根结点，findFather()；②合并，Union()。

但是做题目的时候一定要细心一点，代码能简单就简单，思路有些复杂有些笨那都不是事，只要能保证代码描述的逻辑是正确的就是好代码（因为复杂度分析主要在于空间和时间，OJ上无非就是数组太大内存超限，或者算法太慢时间超限两种情况），千万不要像我一样非得用个max函数更新最大值结果还用错了，导致自己半天没查出错来，这种算法正确但是被小错误坑到的情况是最头疼的o(╥﹏╥)o。

最后还想说的一点是，并查集的题目最好不要用map，比如最后一题有10⁷这么多的编号，虽然map看上去很省空间，但是读下标的操作可没数组这么快。