深度学习笔记(3)基于Tensorflow的多元线性回归:预测波士顿房价
问题描述
给定波士顿地区一系列地区租房的价格,然后罗列出了收集到多个因素,每个因素已经是量化好。现在给定的要求是,使用一个多元线性模型去拟合这些数据,然后用于预测。
模型
p r i c e = f ( x 1 , x 2 , . . . , x n ) = ∑ i = 1 n w i x i + b price = f(x_1, x_2, ..., x_n) = \sum\limits_{i=1}^{n} w_i x_i + b price=f(x1,x2,...,xn)=i=1∑nwixi+b
这里没有激活函数,所以还不到神经网络的阶段。
基于Tensorflow的建模一般步骤
- 数据准备:
1. 筛选
2. 分类
3. 清洗
4. 格式化 - 模型构建
1. 线性模型
2. 非线性模型
3. 神经网络 - 训练模型:确定参数的值
- 评估模型(线性回归不需要这一步)
- 进行预测(这是训练的最终目的)
1. 数据读取
数据下载 提取码:x6if
本次数据使用的是CSV文件,CSV是 comma-separated vaules, 代表文本中的数据均由都好分隔。对于数据的读取,有现成的pandas函数。
%matplotlib notebook
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.utils import shuffle # 用于数据顺序打乱
# 使用pandas
df = pd.read_csv("data/boston.csv", header=0)
df = np.array(df) # 转换成 np.array格式
2. 构建模型
# 占位符
x = tf.placeholder(tf.float32, [None, 12], name = "X") # None 表示行的数量任意,而列必须是12; 此处行表示样本数量
y = tf.placeholder(tf.float32, [None, 1], name = "Y")
# 定义模型函数
# 定义了一个命名空间
with tf.name_scope("Model"): # 打包节点,方便查看计算图
# w 初始化值为shape = (12, 1)的符合正态分布的随机数; 因为 特征值数据的shape是 12 列,w 为了能跟它相乘, 必须是12行
w = tf.Variable(tf.random_normal([12, 1], stddev=0.01), name = "W") # name 应该是用在计算图上面
# b 定义和初始化
b = tf.Variable(1.0, name = "b")
# 定义模型的表达式
def model(x, w, b):
return tf.matmul(x, w) + b # 矩阵乘法,注意 x 和 w 的先后顺序
# y预测值,前向计算节点
predict = model(x, w, b)
上面的语法是常规的tensorflow语法,模型就是简单的线性模型
3. 模型训练
# 迭代轮次
train_epochs = 200
# 学习率
learning_rate = 0.01
# 定义均方差损失函数
# 定义损失函数
with tf.name_scope("LossFunction"):
loss_function = tf.reduce_mean(tf.pow(y - predict, 2)) # 均方误差
# 选择和设置优化器
创建优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)
tensorflow 是以Session() 作为主体进行训练,因此初始化一个Session(),开始训练
sess = tf.Session()
# 定义初始哈变量的操作
init = tf.global_variables_initializer()
sess.run(init) # 代替了对象里面的初始化函数
开始训练
for epoch in range(train_epochs):
loss_sum = 0.0
for xs, ys in zip(x_data, y_data):
xs = xs.reshape(1, 12) # 一行12列,得跟定义的占位符匹配,这里使用reshape,可以确保下面的计算不出现维度不匹配的情况
ys = ys.reshape(1, 1)
_, loss = sess.run([optimizer, loss_function], feed_dict={x: xs, y:ys})
loss_sum += loss
# 训练完打乱数据顺序, 教程里面的代码是错的,因为没有给 x_data,y_data赋值,数据顺序没变
x_data, y_data = shuffle(x_data, y_data)
b0temp = b.eval(session=sess) # 指明哪个对象的 b
w0temp = w.eval(session=sess)
loss_average = loss_sum / len(y_data)
print("epoch", epoch+1, "loss=", loss_average, 'b=', b0temp, 'w=', w0temp)
4. 错误分析
跟着上面的流程,你会发现训练没法进行,这是因为本例采用的12个特征量,取值范围差异极大
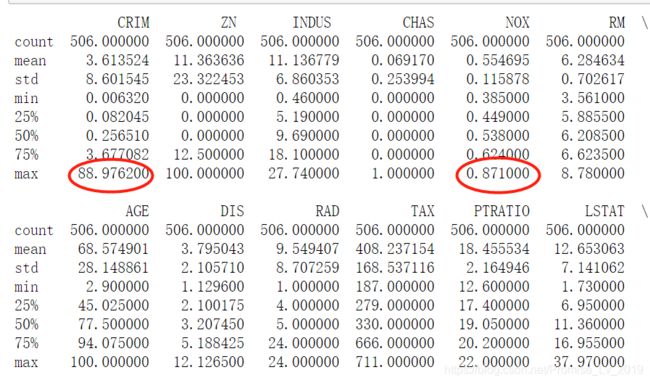
比如第1列数据,CRIM最大值是 88.97, 而第5列最大值才 0.87,这就决定了,程序在梯度优化时,很难准确运行。因此,我们需要先对数据进行归一化,把他们都映射到 ( 0 , 1 ) (0, 1) (0,1)区间,这样程序便能正确调整参数。
5. 数据归一化
注意:归一化,只有自变量 x x x需要, y y y只是标签。
x_data_1 = (x_data - np.min(x_data, axis=0)) / (np.max(x_data, axis = 0) - np.min(x_data, axis=0))
6. 重新训练
for epoch in range(train_epochs):
loss_sum = 0.0
for xs, ys in zip(x_data_1, y_data):
xs = xs.reshape(1, 12) # 一行12列,得跟定义的占位符匹配,这里使用reshape,可以确保下面的计算不出现维度不匹配的情况
ys = ys.reshape(1, 1)
_, loss = sess.run([optimizer, loss_function], feed_dict={x: xs, y:ys})
loss_sum += loss
# 训练完打乱数据顺序, 教程里面的代码是错的,因为没有给 x_data,y_data赋值,数据顺序没变
x_data_1, y_data = shuffle(x_data_1, y_data)
b0temp = b.eval(session=sess) # 指明哪个对象的 b
w0temp = w.eval(session=sess)
loss_average = loss_sum / len(y_data)
print("epoch", epoch+1, "loss=", loss_average, 'b=', b0temp, 'w=', w0temp)