二叉树进阶 --- 二叉搜索树的接口实现

这次我们进入一个全新的领域, 二叉树的进阶部分, 包含了二叉搜索树, STL中的map和set容器, AVl树, 红黑树等高阶数据结构. 今天我们先来研究二叉搜索树的接口实现.

---

---

二叉搜索树的概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

1. 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
2. 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
3. 它的左右子树也分别为二叉搜索树

示例 :

---

---

二叉搜索树的结点描述

一棵树必备的三个元素 (数值, 左孩子指针, 右孩子指针)

//二叉搜索树结点
template <class T>
struct BSTNode {
	T _data;
	BSTNode<T>* _left;
	BSTNode<T>* _right;
	
	//构造函数, 创建新节点时调用
	BSTNode(const T& val = T()) 
		:_data(val)
		,_left(nullptr)
		,_right(nullptr)
	{}
};

---

---

二叉搜索树的接口实现

---

1. 整体框架&构造函数

构造函数直接给空不用多说, typedef为了代码书写方便

template<class T>
class BSTree {
public:
	typedef BSTNode<T> Node;
	
	//构造
	BSTree()
		:_root(nullptr)
	{}

private:
	Node* _root = nullptr;
};

---

2. 查找

二叉树的查找接口逻辑十分简单
从根节点开始搜索
当前结点大于要查找的数据val, 需要找小的值, 向左子树继续遍历
当前结点小于val, 则需要找大的值, 往右子树继续遍历
找到返回当前结点指针即可, 循环结束即为找不到, 返回nullptr

	Node* find(const T& val) {
		//统计查找次数
		int count = 0;

		if (_root == nullptr)
			return _root;

		//从根结点开始搜索
		Node* cur = _root;
		while (cur) {
			count++;
			if (cur->_data == val) {
				cout << "count: " << count << endl;
				return cur;
			}
			else if (cur->_data > val) {
				//要找更小的值, 往左边走
				cur = cur->_left;
			}
			else {
				//往右边走
				cur = cur->_right;
			}
		}

		cout << "count: " << count << endl;
		return nullptr;
	}

---

3. 插入

注意二叉搜索树是没有重复元素的

1.如果是空树, 则创建根节点
2. 非空, 需要先找到要插入的位置和它的父亲结点
3. 根据大小判断插入左边还是右边

查找过程: 和上面的查找过程大致相同, 不过在循环的同时要更新parent结点的位置, 循环结束时cur即为要插入的位置, 我们要通过其父节点parent进入插入操作

下面给一个具体的例子

	//插入 (不存在重复的元素)
	bool insert(const T& val) {
		if (_root == nullptr) {
			//空树, 创建根节点
			_root = new Node(val);
			return true;
		}

		Node* cur = _root;
		Node* parent = nullptr;

		while (cur) {
			//更新父节点
			parent = cur;
			//查找, 整个循环结束后, cur为空, 要插入的位置是parent结点的左边或右边
			if (cur->_data == val)			
				return false; //插入失败
			else if (cur->_data > val)
				cur = cur->_left;
			else
				cur = cur->_right;
		}

		//创建新节点
		cur = new Node(val);
		//插入
		if (parent->_data > val)
			parent->_left = cur;
		else
			parent->_right = cur;
		return true;
	}

---

4. 中序遍历

二叉搜索树有一个重要的性质就是: 中序遍历序列是有序序列

大家可以随便找一棵二叉搜索树验证一下

这里直接用递归的中序遍历
按照 左 — 根 — 右 的顺序进行递归即可

	//中序遍历
	void inorder() {
		_inorder(_root);
		cout << endl;
	}

	void _inorder(Node* root) {
		if (root) {
			_inorder(root->_left);
			cout << root->_data << " ";
			_inorder(root->_right);
		}
	}

---

5. 删除

首先查找元素是否在二叉搜索树中，如果不存在，则返回
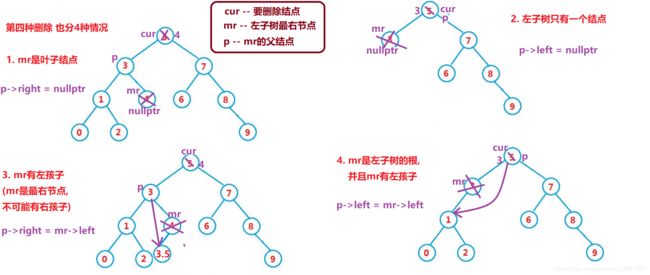
否则要删除的结点可能分下面四种情况：

• 无孩子结点 (叶子)
• 只有左孩子结点
• 只有右孩子结点
• 有左、右孩子结点

---

下面给出图解:

---

根据上述逻辑写出代码 :

注意这里搜索的时候不能和插入一样, 进入循环就更新parent结点,
应该在cur更新的时候才更新parent结点
因为这里的循环是要中途跳出的, 如果一进循环就使parent = cur, 那么找到结点要跳出时, parent也是等于cur的,这显然不是我们要的结果

	//删除
	bool erase(const T& val) {
		if (_root == nullptr)
			return false;

		//搜索
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur) {
			if (cur->_data == val)
				break;
			else if (cur->_data > val) {
				parent = cur;
				cur = cur->_left;
			}
			else {
				parent = cur;
				cur = cur->_right;
			}
		}

		//数据不存在
		if (cur == nullptr)
			return false;
		
		//删除逻辑
		//1. 叶子结点
		if (cur->_left == nullptr && cur->_right == nullptr) {
			//是否为根节点
			if (cur == _root) {
				//删除之后变为空树
				_root = nullptr;
			}
			else {
				//cur在parent的哪边, 就把哪边置空
				if (parent->_left == cur)
					parent->_left = nullptr;
				else
					parent->_right = nullptr;
			}			

			delete cur;
		}
		//2. 非叶子: 左孩子不存在
		else if (cur->_left == nullptr) {
			//如果是根, 直接让右孩子当做新的根节点
			if (cur == _root) {
				_root = cur->_right;
			}
			else {
				//cur只有右孩子, 
				//cur在parent的哪边, 就把cur的右孩子放在parent哪边
				if (parent->_left == cur)
					parent->_left = cur->_right;
				else
					parent->_right = cur->_right;
			}

			delete cur;
		}
		//3. 非叶子: 右孩子不存在
		else if (cur->_right == nullptr) {
			//如果是根, 直接让左孩子作为新的根节点
			if (cur == _root) {
				_root = cur->_left;
			}
			else {
				//cur只有左孩子
				//cur在parent的哪边, 就把cur的左孩子放在parent哪边
				if (parent->_left == cur)
					parent->_left = cur->_left;
				else
					parent->_right = cur->_left;
			}

			delete cur;
		}
		//4. 非叶子: 左右孩子都存在
		else {
			//首先找左子树的最右结点
			Node* mostRight = cur->_left;
			parent = cur;
			while (mostRight->_right) {
				parent = mostRight;
				mostRight = mostRight->_right;
			}

			//最右结点的值存入待删除的结点: cur
			cur->_data = mostRight->_data;
			
			//删除最右结点
			/*
				四种情况
				parent->_right = nullptr
				parent->_left = nullptr
				parent->_right = mostRight->_left
				parent->_left = mostRight->_left
			*/
			
			//这里将情况综合, 首先mr不可能有右孩子
			//如果mr是parent的左孩子, 就把mr的左孩子放在parent的左边
			//mr是叶子,mr的左孩子就是空, 不是叶子, 也能把左孩子给到parent
			//在parent右边也是一样
			if (parent->_left == mostRight)
				parent->_left = mostRight->_left;
			else
				parent->_right = mostRight->_left;

			delete mostRight;

			/*
			* 找右子树的最左结点
			Node* mostLeft = cur->_right;
			parent = cur;
			while (mostLeft->_left) {
				parent = mostLeft;
				mostLeft = mostLeft->_left
			}
			cur->_data = mostLeft->_data;
			if (parent->_left == mostLeft)
				parent->_left = mostLeft->_right;
			else
				parent->_right = mostLeft->_right;

			delete mostLeft;
			*/
		}

		return true;
	}

---

6. 拷贝构造

根据前序遍历的逻辑进行递归, 递归创建并连接节点

	Node* copyTree(Node* root) {
		if (root) {
			Node* node = new Node(root->_data);
			node->_left = copyTree(root->_left);
			node->_right = copyTree(root->_right);
			return node;
		}
		return nullptr;
	}

	//拷贝构造
	BSTree(const BSTree<T>& bst) {
		_root = copyTree(bst._root);
	}

---

7. 赋值运算符重载

国际惯例, 赋值的两种写法
1. 调用上面的拷贝函数, 进行内容深拷贝
2. 现代写法: 传参时传值, 在传参时完成深拷贝, 交换指针即可

	//赋值运算符
	BSTree<T> operator=(const BSTree<T>& bst) {
		if (this != &bst) {
			destory(_root);
			_root = copyTree(bst._root);
		}
		return *this;
	}

	//赋值运算符, 现代写法
	BSTree<T> operator=(BSTree<T> bst) {
		swap(_root, bst._root);
		return *this;
	}

---

8. 析构

后序遍历的顺序, 保证当前结点删除时左右子树已经被删除
递归销毁即可

	void destory(Node* root) {
		if (root) {
			destory(root->_left);
			destory(root->_right);
			delete root;
		}
	}

	~BSTree() {
		destory(_root);
		_root = nullptr;
	}

---

---

接口测试

1. 插入&中序遍历测试

void test() {
	BSTree<int> b;
	b.insert(10);
	b.insert(5);
	b.insert(15);
	b.insert(3);
	b.insert(0);
	b.insert(2);
	b.insert(13);
	b.insert(17);

	//中序遍历: 有序序列
	b.inorder();
}

运行结果如下:

有序序列, 证明我们的代码没有问题

---

2. 查找测试

这里给100000随机数, 我们来查找最大值

void test2() {
	srand(time(nullptr));
	int num;
	cout << "num: ";
	cin >> num;

	BSTree<int> b;
	for (int i = 0; i < num; i++) {
		b.insert(rand());
	}
	b.inorder();
	cout << "search num: ";
	cin >> num;
	b.find(num);
}

运行结果如下:

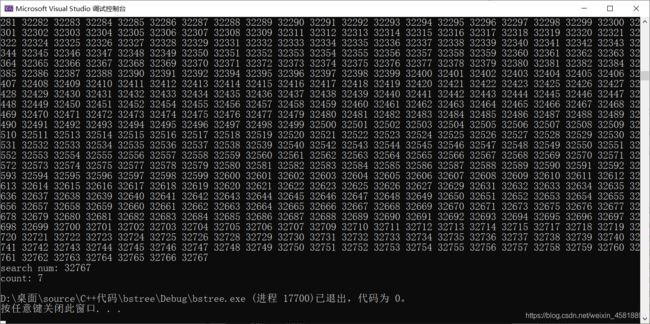
可以看到查找最大数据, 只用了7次, 可见查找效率非常高

---

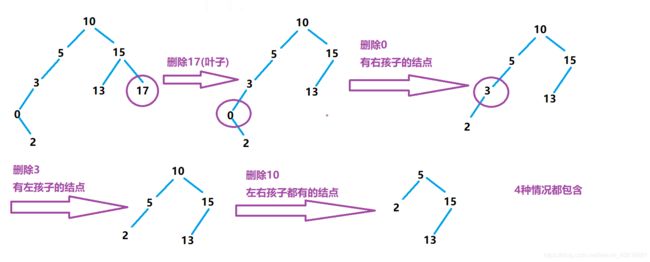
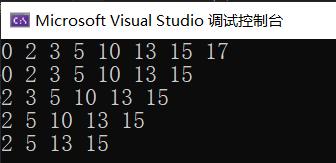
3. 删除测试

void test3() {
	BSTree<int> b;
	b.insert(10);
	b.insert(5);
	b.insert(15);
	b.insert(3);
	b.insert(0);
	b.insert(2);
	b.insert(13);
	b.insert(17);

	b.inorder();

	b.erase(17);
	b.inorder();

	b.erase(0);
	b.inorder();

	b.erase(3);
	b.inorder();

	b.erase(10);
	b.inorder();
}

运行结果如下:

可见都是有序序列, 说明删除正确

---

4. 拷贝构造&赋值测试

void test4() {
	BSTree<int> b;
	b.insert(10);
	b.insert(5);
	b.insert(15);
	b.insert(3);
	b.insert(0);
	b.insert(2);
	b.insert(13);
	b.insert(17);

	b.inorder();

	BSTree<int> copy(b);
	copy.inorder();
	BSTree<int> b2;
	b2 = b;
	b2.inorder();
}

运行结果如下:

结果正确

---

---

二叉搜索树的性能分析