基于到达时间差(TDOA)的室内定位(/无线传感器网络定位)——极大似然估计ML
基于到达时间差(TDOA)的室内定位(/无线传感器网络定位)——极大似然估计ML
原创不易,路过的各位大佬请点个赞
针对AOA,TOA,TDOA,RSS等室内定位、导航的探讨、技术支持、==代码(有偿)==欢迎联系,也可以站内私信,也可以基于其它算法,ML只是一个例子来讲解室内定位
WX: ZB823618313
基于到达时间差(TDOA)的室内定位(/无线传感器网络定位)——极大似然估计ML
- 基于到达时间差(TDOA)的室内定位(/无线传感器网络定位)——极大似然估计ML
-
- 1. 室内定位/无线传感器网络定位技术
-
- 1.1. 室内定位/无线传感器网络定位分类
- 1.2. 室内定位/无线传感器网络定位特点
- 1.3. 室内定位/无线传感器网络定位技术分类
- 1.4. 室内定位/无线传感器网络定位技术比较
- 2. TDOA定位介绍
-
- 2.1 TDOA定位原理
- 2.2 TDOA拓扑图
- 2.3 TDOA与TOA对比
- 2.4 TDOA定位测量
- 3. TDOA定位算法概述
- 4. ML最大似然估计TDOA定位
-
- 4.1. 问题描述
- 4.2. ML估计
- 5. 仿真结果 1
-
- 5.1. 仿真场景
- 5.2. 定位误差RMSE(蒙特卡洛实现)
1. 室内定位/无线传感器网络定位技术
近年来,随着无线通信、集成电路、传感器以及微电系统等技术的飞速发展和日益成熟,被誉为全球未来三大高科技产业之一的无线传感器网络(WSN,Wireless Sensor Network)引起了全世界范围的广泛关注。随着物联网概念的提出,作为其关键技术的传感器技术成为人们研究核心,随着无线传感器网络的应用逐渐深入到人们生活的方方面面,其核心支撑的节点定位技术也得到不断的改进、推广。
1.1. 室内定位/无线传感器网络定位分类
无线传感器网络定位中,存在两类情况:对网络内检测节点的自定位、对未知目标源的盲定位。
节点的自定位:
通过节点自身携带的GPS定位设备等设备获得自身的精确定位,通过自定位系统获得的自身定位的节点称为信标节点也叫做锚节点。
节点的盲定位:
根据信标节点,通过某种定位机制确定未知目标源的位置。节点的盲定位可分为两类:有源定位和无源定位。
有源定位:
网络中监测节点利用有源设备(雷达、激光、声纳等)向被定位目标发射用于定位的各种信号,然后接收被监测目标的返回信号,通过一系列测量、处理得到目标源位置的过程。
优点: 全天候、高精度
缺点: 无隐蔽性、易受电子干扰
无源定位:
网络中监测节点在定位过程中不向被定位目标发射信号(电磁或其他用于定位的信号),监测节点与被监测设备间无协作通讯,监测节点仅通过对目标上发射的电磁信号的搜索、测量、处理而得到目标的位置及参数信息,从而实现定位追踪。
优点: 反侦察、抗干扰、可进行目标识别(弥补有源雷达的不足)
目前主要研究的定位算法为“被动”无源定位。
被动: 监测网络对被监测目标无法进行控制,无法按照自身定位需求添加软硬件支持。
1.2. 室内定位/无线传感器网络定位特点
基于无线传感器网络的信号无源定位与跟踪具有如下特点:
无源定位,直接定位的一方不向目标信号发送信号
多站协同,监测节点需在多次测量、空间移动,或多站间有信息交互协作
运算量大,获取目标位置所需计算量高于其他信息的处理
定位精度、系统内参和定位节点的个数及布局相关
1.3. 室内定位/无线传感器网络定位技术分类
基于距离的定位算法通过测量不同节点到目标信号间的距离或角度信息,利用最大似然估计定位法、三角测量定位法、三边测量定位法估计未知目标节点的位置。
常用定位技术:
- 到达角度技术(AOA)
- 达到时间技术(TOA)
- 到达时间差技术(TDOA)
- 接收信号能量技术(RSSI)
1.4. 室内定位/无线传感器网络定位技术比较
| 技术名称 | 定位精度 | LOS/NLOS | 定位信息 | 优点 | 缺点 |
|---|---|---|---|---|---|
| AOA | 中、高 | LOS | 角度 | 只需要两个接收器。 不需要同步时间 | 需要天线阵列、价格昂贵 |
| TOA | 高 | LOS | 距离 | 精度高 | 需要三个接收器、发射源和目标均时间同步 |
| TDOA | 高 | LOS | 距离差 | 精度高,仅需要同步发射源的始终 | LOS假设 |
| RSS | 低 | both | 信号强度 | 简单、成本低 | 三个节点、精度低 |
2. TDOA定位介绍
2.1 TDOA定位原理
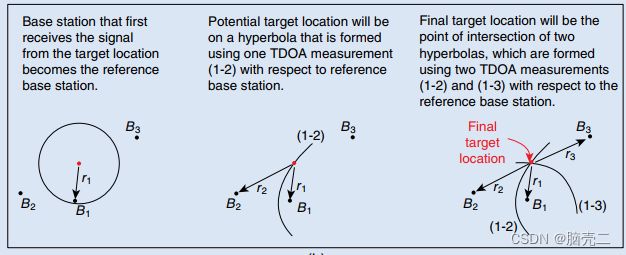
核心思想: TDOA定位是一种利用时间差进行定位的方法。通过测量信号到达监测站的时间,可以确定信号源的距离。利用信号源到各个监测站的距离(以监测站为中心,距离为半径作圆),就能确定信号的位置。但是绝对时间一般比较难测量,通过比较信号到达各个监测站的绝对时间差,就能作出以监测站为焦点,距离差为长轴的双曲线,双曲线的交点就是信号的位置。
不同于TOA,TDOA(到达时间差)是通过检测信号到达两个基站的绝对时间差,而不是到达的飞行时间来确定移动台的位置,降低了信号源与各个监测站的时间同步要求,但提高了各个监测站的时间同步要求。采用三个不同的基站可以测到两个TDOA,移动站位于两个TDOA决定的双曲线的交点上。TDOA值的获取一般有2种形式:
-
第1种形式是利用移动台到达2个基站的时间TOA,取其差值来获得,这时仍需要基站时间的严格同步,但是当两基站间移动信道传输特性相似时,可减少由多径效应带来的误差,
-
第2种形式是将一个移动台接收到的信号与另一个移动台接收到的信号进行相关运算,从而得到TDOA的值,这种算法可以在基站和移动台不同步时,估计出TDOA的值,由于实际应用中,往往很难做到基站与移动台的同步,所以利用相关估计得到TDOA值,再进行定位计算能获得较高精度。对于蜂窝网中的移动台定位而言,TDOA更具有实际意义,这种方法对网络的要求相对较低,并且定位精度较高,已经成为研究的热点。
2.2 TDOA拓扑图
定位原理:TDOA 定位方法,主要是根据测量接收信号在两个基站到目标节点的到达时间做差,然后转换为距离差,从而进行定位。该方法至少需要三个基站,才能计算目标的位置,其定位示意图如图所示。
2.3 TDOA与TOA对比
2.4 TDOA定位测量
数学上、将TDOA乘以已知的传播速度(用c表示),可以得到源和接收器之间的距离差。例如, c ≈ 340 m s − 1 c≈ 340ms^{−1} c≈340ms−1和 c ≈ 3 × 1 0 8 m s − 1 c≈ 3×10^8ms^{−1} c≈3×108ms−1分别是空中场景中的声速和光速。
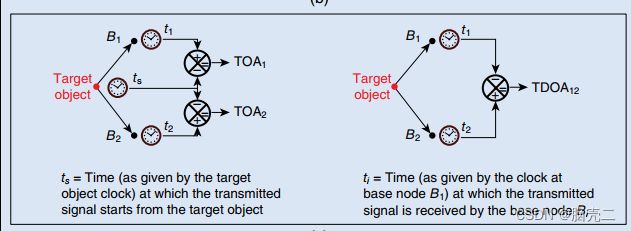
我假设发射源在 t 0 t_0 t0时发射信号,而每个传感器 i , 1 , 2 , ⋯ , N i,~1,2,\cdots,N i, 1,2,⋯,N 分别在时间 t i t_i ti接受到信号。在这些传感器节点中,选择一个参考传感器。不失一般性,我们选择第1个传感器为参考传感器,则到达时间差TDOA为
t T D O A = t i − t 1 , i = 2 , 3 , ⋯ , N t_{TDOA}=t_i-t_1,~i=2,3, \cdots,N tTDOA=ti−t1, i=2,3,⋯,N
测量原理:
TDOA 定位方法,主要是根据测量接收信号在基站和移动台之间的到达时间,然后转换为距离,从而进行定位。
图中BS1假设为发射源,即被定为目标。
假设传感器节点BS到发射源MS 的距离为
d i = ( x − x i ) 2 + ( y − y i ) 2 d_i=\sqrt{(x-x_i)^2+(y-y_i)^2} di=(x−xi)2+(y−yi)2
其中 x = [ x , y ] ′ \mathbf{x}=[x,y]' x=[x,y]′为发射源的位置,即被定位的参数, y i = [ x i , y i ] ′ \mathbf{y}_i=[x_i,y_i]' yi=[xi,yi]′为第i个锚节点的位置,假设存在N个锚节点构成传感器网络,则 i = 1 , 2 , ⋯ , N i=1,2,\cdots,N i=1,2,⋯,N。
数学上、将TDOA乘以已知的传播速度(用c表示),可以得到源和接收器之间的距离差。例如, c ≈ 340 m s − 1 c≈ 340ms^{−1} c≈340ms−1和 c ≈ 3 × 1 0 8 m s − 1 c≈ 3×10^8ms^{−1} c≈3×108ms−1分别是空中场景中的声速和光速。我假设发射源在 t 0 t_0 t0时发射信号,而每个传感器 i , 1 , 2 , ⋯ , N i,~1,2,\cdots,N i, 1,2,⋯,N 分别在时间 t i t_i ti接受到信号。在这些传感器节点中,选择一个参考传感器。不失一般性,我们选择第1个传感器为参考传感器,则到达时间差TDOA为
t T D O A , i = t i − t 1 , i = 2 , 3 , ⋯ , N t_{TDOA,i}=t_i-t_1,~i=2,3, \cdots,N tTDOA,i=ti−t1, i=2,3,⋯,N
同TOA一样,在实际中,TDOA也会受到测量误差的影响。因此,基于 t T D O A , i t_{TDOA,i} tTDOA,i乘以 c c c的距离测量,定义为 r T D O A , i r_{TDOA,i} rTDOA,i,可以建模为
r T D O A , i = d i − d 1 + n i = ( x − x i ) 2 + ( y − y i ) 2 − ( x − x 1 ) 2 + ( y − y 1 ) 2 + n i , i = 2 , ⋯ , N \begin{aligned} r_{TDOA,i}&=d_i-d_1+n_i\\ &=\sqrt{(x-x_i)^2+(y-y_i)^2}-\sqrt{(x-x_1)^2+(y-y_1)^2}+n_i, ~ i=2,\cdots,N \end{aligned} rTDOA,i=di−d1+ni=(x−xi)2+(y−yi)2−(x−x1)2+(y−y1)2+ni, i=2,⋯,N
其中 n i n_i ni 为测量噪声,来源于TDOA的干扰。
3. TDOA定位算法概述
主要算法: 基于AOA技术的室内定位可以分为两大类方法:参数估计算法和滤波方法。
1-参数估计算法主要解决非移动目标(如传感器节点、发射源等)的定位问题,主要包括:
ML最大似然估计
LS最小二乘估计
WLS加权最小二乘估计
NLS非线性最小二乘估计
凸规划
**注意:**这类方法也可以解决移动目标的室内外定位问题。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
2- 滤波方法主要解决移动目标(如智能小车、移动机器人、移动终端等)的室内外定位问题,主要包括:
扩展卡尔曼滤波EKF
无迹卡尔曼滤波UKF
容积卡尔曼滤波CKF
求积卡尔曼滤波QKF
中心差分卡尔曼滤波CDKF
Divided difference filter DDF
高斯混合滤波GSF
强跟踪滤波STF
粒子滤波PF
… …
4. ML最大似然估计TDOA定位
4.1. 问题描述
考虑N个传感器网络,我假设发射源在 t 0 t_0 t0时发射信号,而每个传感器 i , 1 , 2 , ⋯ , N i,~1,2,\cdots,N i, 1,2,⋯,N 分别在时间 t i t_i ti接受到信号。在这些传感器节点中,选择一个参考传感器。不失一般性,我们选择第1个传感器为参考传感器,则到达时间差TDOA为
t T D O A , i = t i − t 1 , i = 2 , 3 , ⋯ , N t_{TDOA,i}=t_i-t_1,~i=2,3, \cdots,N tTDOA,i=ti−t1, i=2,3,⋯,N
同TOA一样,在实际中,TDOA也会受到测量误差的影响。因此,基于 t T D O A , i t_{TDOA,i} tTDOA,i乘以 c c c的距离测量,定义为 r T D O A , i r_{TDOA,i} rTDOA,i,可以建模为
r T D O A , i = d i − d 1 + n i = ( x − x i ) 2 + ( y − y i ) 2 − ( x − x 1 ) 2 + ( y − y 1 ) 2 + n i , i = 2 , ⋯ , N \begin{aligned} r_{TDOA,i}&=d_i-d_1+n_i\\ &=\sqrt{(x-x_i)^2+(y-y_i)^2}-\sqrt{(x-x_1)^2+(y-y_1)^2}+n_i, ~ i=2,\cdots,N \end{aligned} rTDOA,i=di−d1+ni=(x−xi)2+(y−yi)2−(x−x1)2+(y−y1)2+ni, i=2,⋯,N
其中 n i n_i ni 为测量噪声,来源于TDOA的干扰。
4.2. ML估计
基于N个锚节点的TOA测量,构造似然函数:
P ( r T D O A ∣ x ) = ∏ i = 1 N 1 2 π σ i e − ( r T D O A , i − h ( x ) ) 2 2 σ i 2 P(\mathbf{r_{TDOA}}|\mathbf{x})=\prod_{i=1}^N\frac{1}{\sqrt{2\pi}\sigma_i}e^{-\frac{(r_{TDOA,i}-h(\mathbf{x}))^2}{2\sigma_i^2}} P(rTDOA∣x)=i=1∏N2πσi1e−2σi2(rTDOA,i−h(x))2
其中
h ( x ) = ( x − x i ) 2 + ( y − y i ) 2 − ( x − x 1 ) 2 + ( y − y 1 ) 2 h(\mathbf{x})=\sqrt{(x-x_i)^2+(y-y_i)^2}-\sqrt{(x-x_1)^2+(y-y_1)^2} h(x)=(x−xi)2+(y−yi)2−(x−x1)2+(y−y1)2
取对数、得到对数似然函数:
L ( x ) = c + ∑ i = 1 N − 1 2 σ i 2 ( r T D O A , i − h ( x ) ) 2 L(\mathbf{x})=c+ \sum_{i=1}^N-\frac{1}{2\sigma_i^2}(r_{TDOA,i}-h(\mathbf{x}))^2 L(x)=c+i=1∑N−2σi21(rTDOA,i−h(x))2
其中 c c c为常数。
则发射源的最大似然估计为:
x ^ = arg max L ( x ) = arg min ∑ i = 1 N 1 2 σ i 2 ( r T D O A , i − h ( x ) ) 2 \begin{aligned} \hat{\mathbf{x}}&=\arg \max L(\mathbf{x})\\ &=\arg \min \sum_{i=1}^N\frac{1}{2\sigma_i^2}(r_{TDOA,i}-h(\mathbf{x}))^2 \end{aligned} x^=argmaxL(x)=argmini=1∑N2σi21(rTDOA,i−h(x))2
5. 仿真结果 1
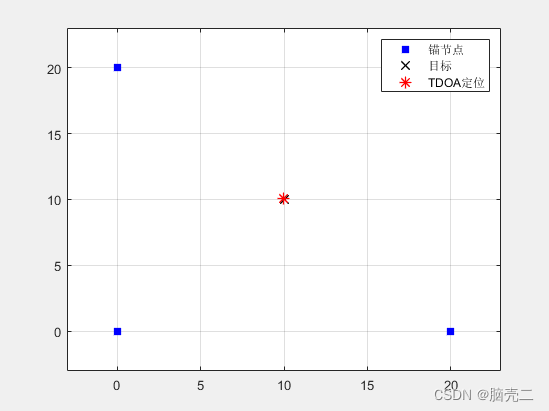
5.1. 仿真场景
考虑4个传感器节点,一个目标节点。
定位结果:
TDOA定位结果:
10.0067
10.0299
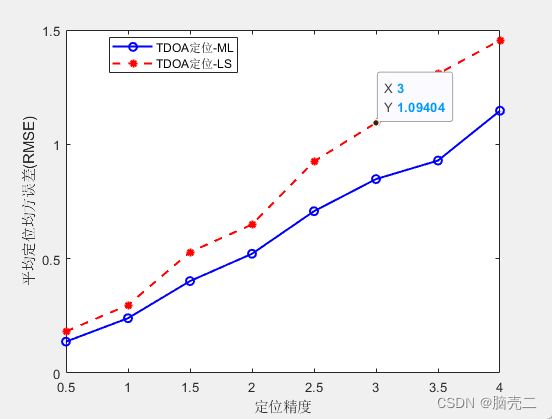
5.2. 定位误差RMSE(蒙特卡洛实现)
TDOA定位结果:
Target_position_ML =
10.0202 9.8870 9.9408 10.7513 9.0884 9.8172 9.9751 9.4494
10.0533 10.2017 9.7053 9.9880 10.1940 9.7524 11.1078 10.4629
*原创不易,路过的各位大佬请点个赞