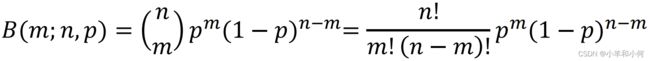机器学习基础：概率和熵
目录
1. 概率
1.1 变量类型
1.2 概率基础
1.2.1 边际概率
1.2.2 联合概率
1.2.3 条件概率
1.2.4 先验概率，后验概率
1.2.5 事件的独立和条件独立
1.3 概率分布
1.3.1 实验概率分布（empirical probability）
1.3.2 理论概率分布
1.4 概率模型（Probability models）
2. 信息熵
2.1 二项分布的信息熵
2.2 多项分布的信息熵
2.3 信息熵和信息编码
2.3.1 字母编码
2.3.2 图像编码
1. 概率
1.1 变量类型
其中每一行就是一个
。
每一列就是一个
。
如果你要对数据进行机器学习任务，那么你就要指定一列数据作为
。
因此
例子：
要求根据 “姓名”，“年龄”，“身高”，“是否婚恋”，“学历”这些特征来进行预测“月薪”。
那么这个时候“月薪”这一列就是，而其他的列就是
，很多任务里我们也把 称为特征，
叫做标签。
张三以及张三所有的信息称为一条也叫一条数据。
根据中数据类型的不同，我们可以把他们分为：
：
通过名称来区分类型，例如“张三”，“李四”这些变量互相之间没有任何关系；这些变量之间也不存在顺序关系，他们相互之间是
的。
类型是一类特殊的
。
：
变量值是离散的，而且不同的变量值之间存在天然的顺序，数学运算通常没有意义。例如酒店评级，三星，五星；其中
是离散的值，但是不能进行数学运算，因为
星
星
星，但是这违背了数据本身的意义，加完之后就变成了没有意义的数据。
（
）：
变量值本身是实数，没有明显的数据边界，例如：距离，时间，价格；两个值之间是连续的，可以进行有意义的数学运算，例如
。
等同差异，那么什么是不等同差异呢，比如当我们做分类任务的时候我们区分猫、狗、人，猫和狗之间的差异与人和狗之间的差异显然是不一样的，虽然猫和狗不同，人也和狗不同，但是这种’不同’ 仍然不是等价的。而这个时候（猫或狗或人的）名字之间虽然不同，但是这种不同我们可以认为是
的，这个名字属性并不会对分类这个任务产生任何影响，换句话说，就算你换了一个名字，依然不影响分类任务。但换到另外一类任务中，可能名字就不是
变量的类型之所以重要，是因为我们需要不同的处理方法，我们要避免无效和无意义的操作或者产生无意义的
。
1.2 概率基础
我们之所以需要概率，是因为我们所处的世界和所面对的绝大多数情况，都是不确定的；当我们和别人擦肩而过的时候，我们喜欢猜他们的身份，帅气阳光、谈吐不凡的小伙大概率家境优渥，美丽而性感的女孩大概率是开朗的，而猜的过程就是一个通过观测到的已知信息进行概率预测的过程。
1.2.1 边际概率
假设我们现在有两个事件
代表年龄；
代表购买情况，也就构成了上面这张表格。
或者
我们称为边际概率，他们是上表中的一整行或者一整列，所以我们叫他们“边际”概率：
还是举个具体的例子帮助理解：校园里随便抓一个人 > 45 岁的概率是多少，数学表示可以是
或者写成
；
这个概率是多少呢？当然是
(所有值)
。
1.2.2 联合概率
联合概率就是两个事件同时发生的概率，例如：
也可以简写成
这个概率也很容易算出来，是
1.2.3 条件概率
在一个事件发生的前提下，另外一个事件发生的概率。数学形式上写作
读作：在 
事件发生的条件下
事件发生的概率。
这个概率，我们也可以通过联合概率和边际概率一起求算条件概率：
概率的计算规则可以总结成下图：
注意，图中的
我们称为小
小
，是
和
事件的其中一种情况，不能认为是或者事件。
1.2.4 先验概率，后验概率
给定这个公式，我们可以得到
同样我们也可以得到；而由这两个公式，我们可以联合得到贝叶斯公式：
或者
我们上文中贝叶斯公式的第一种形式来举例：
是先验概率
。
是后验概率
。
先验概率顾名思义是我们事先知道的概率。例如上面表格的例子中，我们可以通过统计直接得到的概率就是先验概率，例如。
1.2.5 事件的独立和条件独立
独立的两个事件
如果两个事件是完全独立的，两个独立事件相互不影响，一个发生或者不发生并不会影响另外一个的概率。
条件独立的两个事件
假设
是关于
独立的，这个意思就是说，在这个事件发生的时候，可以认为是独立的。
不同事件对结果预测的影响：
1250个样本/观测值
经验概率：
上面的例子中根据贝叶斯公式求得的概率显示，当我们把
作为条件求的概率，而事件只有两种情况
，因此我们很容易通过给定一个情况而判断
的情况，即：如果 
则预测为否则就不。
如果把这个条件和预测的事件调转一下：
当给定事件作为条件，通过贝叶斯公式求得在一种情况下的概率并不能帮我们一下得到预测结果；因为的情况有三种，如果我们想得到所有的情况，我们需要依次计算，例如我们需要分别求得： 
才能判断出来当给定 yes 的条件下哪种人群的概率更大。
1.3 概率分布
一个函数描述了一个随机变量的所有结果的概率 ：
- 对于离散的随机变量，我们使用概率质量函数（probability mass function）
- 对于连续的随机变量，我们采用概率密度函数（probability density function）
1.3.1 实验概率分布（empirical probability）
通过一系列实验或者统计数据得到的概率分布。
1.3.2 理论概率分布
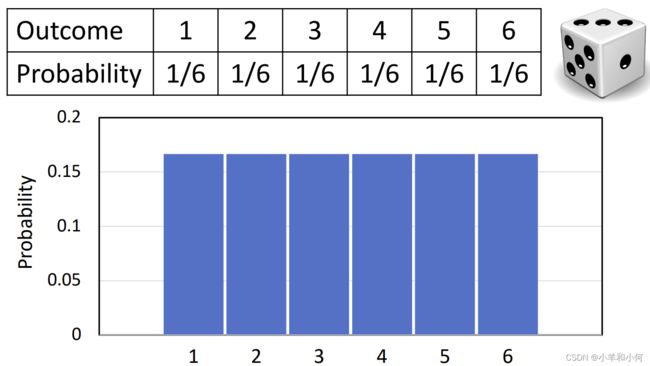
离散的均匀分布（discrete uniform distribution）
离散均匀分布=所有结果的可能性相同
二项分布（伯努利分布）（Binomial Distribution / Bernoulli distribution）
一个事件只有两种发生的可能，概率分别是
和
。
伯努利试验 
一个只有两种可能结果的随机试验（如抽奖）。
二项分布是一系列独立的伯努利试验的结果。
对于
是
的概率，在
次独立的伯努利试验中，有
个的概率。
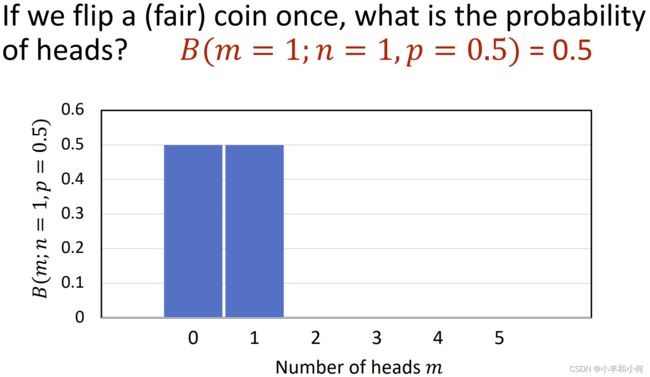
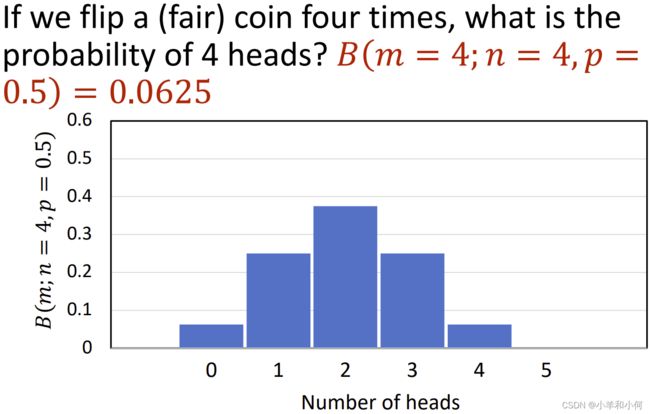
现在有一个事件，扔次硬币，最终次 正面向上；如果我们统计
的情况；那么随着扔硬币的次数越多，这个事件的概率分布趋向于正态分布：
1000次投掷硬币的概率分布：
多项分布（multinomial distribution）
有多个独立的结果的事件组成，例如扔一个六面骰子；每个面出现的概率都是
；这就是一个多项分布。
多项分布是由一系列具有两个以上结果的独立试验产生的。事件
和事件
分别恰好发生
次（
）的概率：
多项式系数：
高斯分布（normal / Gaussian Distribution）
高斯分布通常用来代表噪声连续变量，尤其是噪声类型不知道的情况下，我们通常假设是正态分布的。
由一个具有平均值（期望值）
和标准差
的变量得到观测值的概率：
当
的时候，我们产生的高斯分布叫标准正态分布。
1.4 概率模型（Probability models）
概率模型是通过数学方式来表示随机事件.
概率模型通常有三部分组成：
- 采样空间：所有可能发生的值
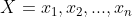
- 事件：采样空间的子集
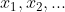
- 关于事件的概率分布
2. 信息熵
信息熵的定义：
信息熵是对不可预测性的一种度量，是预测一个事件发生的依据。
一个独立随机变量
的信息熵是：
假设扔骰子，
，所以
因此，我们用
的信息就可以代表一个骰子的所有情况。
对于一个二项分布来说，
事件发生的概率是则
的概率就是。
因此如果我们计算这个二项分布的信息熵
2.1 二项分布的信息熵
# 我们在这里模拟一下 H(X) 的变化情况
Px = np.arange(0,1,0.01)
y = -Px * np.log2(Px)-(1-Px)*(np.log2(1-Px))
plt.plot(Px,y)
plt.xlabel('P(X=x1)')
plt.ylabel('H(X)')
从上图我们可以看出，当
的时候，
表示的信息量最大，能够表示最多
的信息。信息熵最小的情况发生在两端，即当一个事件（或者）变成确定事件的时候，另外一个也就变成了确定事件，而这个时候，他们就不能够提供任何信息。所以我们可以说“信息量的大小就是对一个事件不确定性的衡量”
2.2 多项分布的信息熵
让我们回顾一下上面骰子的例子，因为
个面的概率是均等的，因此能够表示这个骰子能表示的最多的信息量但如果他们每个面的概率不同，他们表示的信息量就会降低，这是显而易见的。扩展一下，当一个随机变量拥有
个不同的事件，当他们是均匀分布的时候，包含的信息量最大。
信息熵的上限：
- 对于一个只有两种可能结果的系统，信息熵取值范围为
。
- 对于一个有
种可能结果的系统，信息熵取值范围为
。
（最小）熵 0：意味着只有一个结果是可能的（决定性的）。
（最大值）熵
：表示所有结果的可能性相同。
2.3 信息熵和信息编码
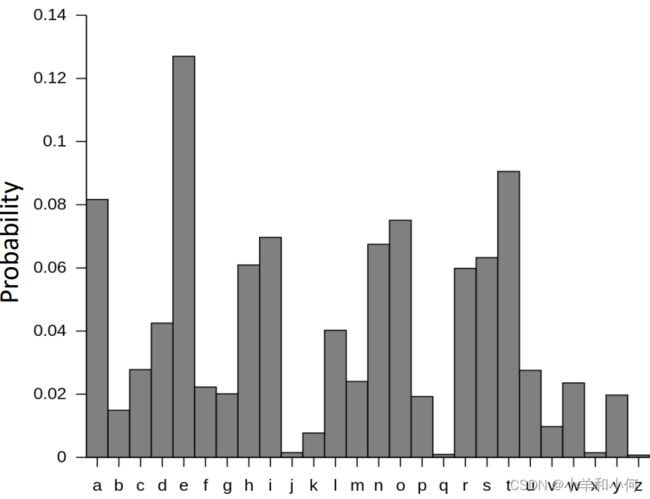
2.3.1 字母编码
我们对大英图书馆中所有的书进行统计，里面的字符的概率分布如上图所示；
个英文字母能够包含的最大信息量是
（当所有字母等可能出现）
但是根据实际情况，他们的
实际上是
。
因此实际上只用 
个不同的字母就可以对现在的系统重新编码。
2.3.2 图像编码
如何使用有限的带宽资源来传输更多的信息？
