AI算法工程师 | 04人工智能基础-高等数学知识强化（四）线性代数基础之矩阵

数学知识 之 线性代数基础

矩阵及其运算

矩阵就是二维数组，下面是一个 m 乘 n 的矩阵

• 该矩阵有 m 行 n 列，每行每列上面都有一个元素
• 每个元素都有行标 $i$ 和列标 $j$，第 $i$ 行 第 $j$ 列的元素可表示为：$a_{ij}$
  $$\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{m1}& \cdots & a_{mn}\end{array}\right]$$

特殊的矩阵

ღ 方阵

方阵：如果 m 等于 n，那就称为方阵（行数与列数一致）
$$\left[\begin{array}{ccc}1& 0& 0\\ 4& 0& 2\\ 1& 3& 0\end{array}\right]$$

ღ 对称矩阵

对称矩阵：如果 $a_{ij}$ 等于 $a_{ji}$，则为对称矩阵（沿着主对角线对称）
$$\left[\begin{array}{ccc}1& 1& 2\\ 1& 4& 3\\ 2& 3& 0\end{array}\right]$$

ღ 单位矩阵

单位矩阵：主对角线全为1，其余为0。单位矩阵通常用 $I$ 或 $E$ 来表示，等同于数字里面的 1
$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

Pyhton中的表示

以下是 cmd 命令端中输入python，所进入的 python 交互窗口

• 创建单位矩阵

>>> import numpy as np
>>> np.identity(5)  # 创建单位矩阵（ 5 行 5 列的方阵）
array([[1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.]])
>>> np.identity(3)  # 创建单位矩阵（ 3 行 3 列的方阵）
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
>>> np.eye(5) # 通过 eye 函数 也可创建单位矩阵
array([[1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.]])

• 一个矩阵 $A$ 与单位矩阵 $I$ 做内积，得到的结果与原矩阵 $A$ 相同

>>> np.arange(9) # 创建一组数组
array([0, 1, 2, 3, 4, 5, 6, 7, 8])
>>> A = np.arange(9).reshape(3,3) # 变成 3 行 3 列（二维数组，即：矩阵）
>>> A
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])
>>> I = np.identity(3) # 创建单位矩阵（ 3 行 3 列的方阵）
>>> I
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
>>> A * I # ✘ 代码中这样写，得到的结果有问题-它在进行对应点相乘，而非内积（得到的不是矩阵的乘法）
array([[0., 0., 0.],
       [0., 4., 0.],
       [0., 0., 8.]])
>>> np.dot(A,I) # √ 正确的矩阵的乘法表达（dot表示矩阵乘法，A 与 I 做内积）
array([[0., 1., 2.],
       [3., 4., 5.],
       [6., 7., 8.]])

ღ 对角矩阵

对角矩阵：主对角线非 0，其它位置是 0（单位矩阵是一种特殊的对角矩阵）

$$\left[\begin{array}{ccccc}{\lambda }_1& \cdots & 0& 0& 0\\ \cdots & {\lambda }_2& \cdots & 0& 0\\ 0& \cdots & \cdots & \cdots & 0\\ 0& 0& \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & {\lambda }_n\end{array}\right]$$

小贴士

• 对称矩阵、单位矩阵、对角矩阵等都一定是方阵
• 主对角线：方阵中，从左上角到右下角这一斜线方向上的对角线

矩阵的运算

ღ 加减法、数乘、转置、乘法

加减法：矩阵的加法就是矩阵的对应位置相加，减法也是一样就是对应位置相减
$$\left[\begin{array}{ccc}1& 2& 3\\ 0& 0& 0\end{array}\right]+\left[\begin{array}{ccc}4& 5& 6\\ 0& 0& 0\end{array}\right]=\left[\begin{array}{ccc}5& 7& 9\\ 0& 0& 0\end{array}\right]$$

数乘：对应位置的一个相乘
$$5\times \left[\begin{array}{ccc}1& 2& 3\\ 0& 0& 0\end{array}\right]=\left[\begin{array}{ccc}5& 10& 15\\ 0& 0& 0\end{array}\right]$$

转置：转置的操作和向量是一样的，就是把 $a_{ij}$ 变成$a_{ji}$，把行和列互换一下（$a_{ij}\Rightarrow a_{ji}$）
$${\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\end{array}\right]}^T=\left[\begin{array}{cc}1& 4\\ 2& 5\\ 3& 6\end{array}\right]$$

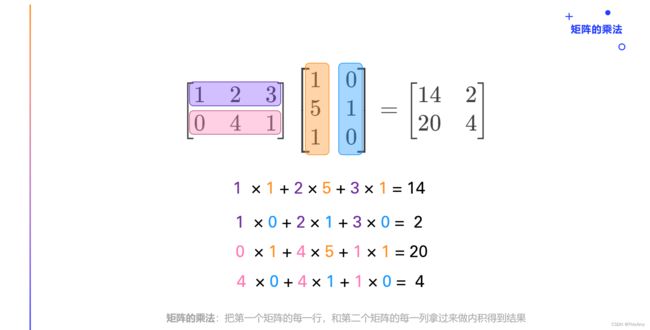
乘法：矩阵的乘法和一般的乘法不太一样

• 它是把第一个矩阵的每一行，和第二个矩阵的每一列拿过来做内积得到结果
• 注意：左边矩阵的列数要与右边矩阵的行数相同，否则无法相乘
• 如：m 行 n 列的矩阵 与 n 行 k 列的矩阵相乘，可得到 m 行 k 列的矩阵（m x n 与 n x k => n x k ）
  $$\left[\begin{array}{ccc}1& 2& 3\\ 0& 4& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ 5& 1\\ 1& 0\end{array}\right]=\left[\begin{array}{cc}14& 2\\ 20& 4\end{array}\right]$$

ღ 代码表示矩阵的运算

Pyhton中的表示

以下是 cmd 命令端中输入python，所进入的 python 交互窗口

• 矩阵的加减法

>>> import numpy as np
>>> np.arange(6) # 创建一维数组
array([0, 1, 2, 3, 4, 5])
>>> a = np.arange(6).reshape(2,3)  # 变成 2 行 3 列的
>>> a
array([[0, 1, 2],
       [3, 4, 5]])
>>> b = np.arange(6).reshape(2,3)
>>> b
array([[0, 1, 2],
       [3, 4, 5]])
>>> a + b  # 矩阵的加法（对应位置相加）
array([[ 0,  2,  4],
       [ 6,  8, 10]])
>>> a - b # 矩阵的减法（对应位置相减）
array([[0, 0, 0],
       [0, 0, 0]])

• 数乘

>>> 5 * a
array([[ 0,  5, 10],
       [15, 20, 25]])

• 转置

>>> # 回忆：向量的转置
>>> v = np.array([1,2,3])
>>> v.T # 该方法，虽然转置了，但展现的还是行向量形式
array([1, 2, 3])
>>> v.reshape(-1,1) # 若要展示成列向量的形式，可通过 reshape 形状变换
array([[1],
       [2],
       [3]])
>>>
>>>
>>> # 矩阵的转置
>>> a
array([[0, 1, 2],
       [3, 4, 5]])
>>> a.T # 方式一：在矩阵中，该方法可实现转置
array([[0, 3],
       [1, 4],
       [2, 5]])
>>> a.reshape(3,2) # ✘ 通过改变形状 无法实现 矩阵的转置
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> 
>>> # 方式二：通过 transpose()函数实现转置
>>> a.shape # 打印 a 的形状（ 2 行 3 列）
(2, 3)
>>> a.transpose(1,0) # 1,0 代表索引号 index，分别指代 a 的形状(2,3)中的 3 和 2 => 把它们颠倒位置，得到 (3,2)=> 3 行 2 列
array([[0, 3],
       [1, 4],
       [2, 5]])
>>> a.T.shape # 该方式得到的是 3 行 2 列矩阵
(3, 2)
>>> a.transpose(1,0).shape # 该方式得到的也是 3 行 2 列矩阵（说明 transpose 方式可实现矩阵的转置）
(3, 2)
>>>
>>>
>>> # 扩展：transpose()函数 可适用于更高维度的数组，如 三维
>>> temp = np.arange(24).reshape(2,3,4) # 三维数组：2 个大块，每大块 为 3 行，4 列
>>> temp
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])
>>> temp.transpose(1,0,2) # transpose()函数的作用：调换数组的索引值 ∴ 由 (2,3,4) =》 变为 (3,2,4)  3个 2行 4列的多维数组
array([[[ 0,  1,  2,  3],
        [12, 13, 14, 15]],

       [[ 4,  5,  6,  7],
        [16, 17, 18, 19]],

       [[ 8,  9, 10, 11],
        [20, 21, 22, 23]]])

• 矩阵的乘法

>>> a # 接着前面所赋给的值
array([[0, 1, 2],
       [3, 4, 5]])
>>> b
array([[0, 1, 2],
       [3, 4, 5]])
>>> a * b # ✘ 这不是矩阵相乘，而是对应位置相乘
array([[ 0,  1,  4],
       [ 9, 16, 25]])
>>>
>>> # 通过 dot 实现矩阵的相乘
>>> np.dot(a,b) # 注意：两个相同形状的矩阵（ 2 行 3 列 ），无法进行相乘
Traceback (most recent call last):
  File "", line 1, in <module>
  File "<__array_function__ internals>", line 180, in dot
ValueError: shapes (2,3) and (2,3) not aligned: 3 (dim 1) != 2 (dim 0)
>>>
>>> # 两矩阵如何才可相乘 ？ 
>>> b.T  # 对 b 进行转置
array([[0, 3],
       [1, 4],
       [2, 5]])
>>> np.dot(a,b.T) # 2 行 3 列 乘以 3 行 2 列 =》 得到 2 行 2 列的矩阵
array([[ 5, 14],
       [14, 50]])
>>> np.dot(b.T,a) # 3 行 2 列 乘以 2 行 3 列 =》 得到 3 行 3 列的矩阵
array([[ 9, 12, 15],
       [12, 17, 22],
       [15, 22, 29]])

ღ 矩阵运算法则

矩阵的加减法

• 满足分配律，结合律，和交换律
• 如：结合律 $A+B+C=A+(B+C)$

矩阵的乘法

• 满足结合律：$(AB)C=A(BC)$
• 满足分配律
  • 左分配律：$(A+B)C=AC+BC$
  • 右分配律：$A(B+C)=AB+AC$
• 不满足交换律：$AB\ne BA$
  • 说明：$AB$ 与 $BA$ 不一定相等，甚至它们的尺寸也不同
  • 举例：
    $AB=\left[\begin{array}{ccc}1& 2& 3\\ 0& 0& 0\end{array}\right]\left[\begin{array}{cc}1& 0\\ 1& 0\\ 1& 0\end{array}\right]=\left[\begin{array}{cc}6& 0\\ 0& 0\end{array}\right]$
    $BA=\left[\begin{array}{cc}1& 0\\ 1& 0\\ 1& 0\end{array}\right]\left[\begin{array}{ccc}1& 2& 3\\ 0& 0& 0\end{array}\right]=\left[\begin{array}{ccc}1& 2& 3\\ 1& 2& 3\\ 1& 2& 3\end{array}\right]$

转置

• 公式：$(AB{)}^T=B^T{A}^T$

>>> # 通过代码验证 转置 的公式
>>> A = np.arange(6).reshape(2,3) # 创建 2 行 3 列的矩阵
>>> A
array([[0, 1, 2],
       [3, 4, 5]])
>>> B = np.arange(10,16).reshape(3,2) # 创建 3 行 2 列的矩阵
>>> B
array([[10, 11],
       [12, 13],
       [14, 15]])
>>> np.dot(A,B)
array([[ 40,  43],
       [148, 160]])
>>> np.dot(A,B).T # AB相乘再转置 
array([[ 40, 148],
       [ 43, 160]])
>>> np.dot(A.T,B.T)
array([[ 33,  39,  45],
       [ 54,  64,  74],
       [ 75,  89, 103]])
>>> np.dot(B.T,A.T) # B的转置 乘 A的转置（结果等于 AB相乘再转置）
array([[ 40, 148],
       [ 43, 160]])

逆矩阵

矩阵有 $AB$，但是没有 $A/B$ 这么一说，只有逆矩阵

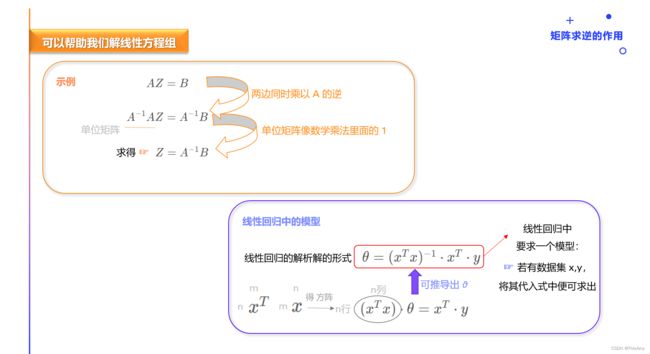
ღ 逆矩阵的定义及其作用

逆矩阵的定义

假设有个矩阵 $A$（一定是方阵），乘以矩阵 $B$ 等于 $I$（$I$ 为单位矩阵），$AB=I$ 或者 $BA=I$，则称 $B$ 为 $A$ 的右逆矩阵、左逆矩阵。

一个结论：如果这样的 $B$ 存在，它的左逆和右逆一定相等，统称为 $A$ 的 $-1$ （$A$ 的逆矩阵）

矩阵求逆的作用

公式

$(AB{)}^{-1}=B^{-1}{A}^{-1}$

$(A^{-1}{)}^{-1}=A$

$(A^T{)}^{-1}=(A^{-1}{)}^T$

ღ 逆矩阵在 numpy 中的求解

Pyhton中的表示

以下是 cmd 命令端中输入python，所进入的 python 交互窗口

• 验证公式 $(A^{-1}{)}^{-1}=A$

>>> import numpy as np
>>> A = np.array([20,245,54,12]).reshape(2,2) # 创建 2 行 2 列的矩阵（方阵）
>>> A      #  A
array([[ 20, 245],
       [ 54,  12]])
>>> A_inv = np.linalg.inv(A) # 矩阵求逆
>>> A_inv
array([[-0.00092379,  0.01886066],
       [ 0.00415704, -0.00153965]])
>>> 
>>> np.linalg.inv(A_inv) # A 逆 的 逆 = A
array([[ 20., 245.],
       [ 54.,  12.]])

• 验证公式 $(A^T{)}^{-1}=(A^{-1}{)}^T$

>>> np.linalg.inv(A.T)  # A 转置 的逆
array([[-0.00092379,  0.00415704],
       [ 0.01886066, -0.00153965]])
>>> np.linalg.inv(A).T  # A 逆 的转置
array([[-0.00092379,  0.00415704],
       [ 0.01886066, -0.00153965]])

小贴士

• numpy.linalg 模块包含线性代数的函数
• np.linalg.inv()：矩阵求逆 （ linalg = linear + algebra ）

-_-

—— 参考：numpy基础教程之np.linalg

行列式

行列式其实在机器学习中用的并不多，一个矩阵必须是方阵，才能计算它的行列式（行列式是把矩阵变成一个标量）

ღ 行列式的计算及其性质

计算方式

$\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|=a_{11}{a}_{22}-a_{12}{a}_{21}$

$\left|\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right|=a_{11}{a}_{22}{a}_{33}+a_{12}{a}_{23}{a}_{31}+a_{13}{a}_{21}{a}_{32}-a_{13}{a}_{22}{a}_{31}-a_{12}{a}_{21}{a}_{33}-a_{11}{a}_{23}{a}_{32}$

行列式的应用

如：① 正态分布中 $\Sigma$ 的行列式并开根号， ${\left|\Sigma \right|}^{\frac{1}{2}}$；② 特征值、特征向量中也会应用到

行列式的性质

$\left|AB\right|=\left|BA\right|$

$\left|A^{-1}\right|={\left|A\right|}^{-1}$

$\left|\alpha A\right|={\alpha }^n\left|A\right|$

小贴士
以上行列式的内容，都是针对方阵而言的

ღ 行列式在 numpy 中的使用

Pyhton中的表示

以下是 cmd 命令端中输入python，所进入的 python 交互窗口

• 验证公式 $\left|A^{-1}\right|={\left|A\right|}^{-1}$

>>> import numpy as np
>>> A = np.arange(4).reshape(2,2) # 创建 2 行 2 列 的方阵
>>> A
array([[0, 1],
       [2, 3]])
>>> 
>>> # 通过 np.linalg.det 可求行列式
>>> np.linalg.det(np.linalg.inv(A)) # A 逆 的 行列式
-0.49999999999999994
>>> 1 / np.linalg.det(A) # A 行列式 的 逆
-0.5

• 验证公式 $\left|\alpha A\right|={\alpha }^n\left|A\right|$

>>> A
array([[0, 1],
       [2, 3]])
>>> 3*A
array([[0, 3],
       [6, 9]])
>>> np.linalg.det(3*A)  # 3 乘 A，的行列式
-17.999999999999996
>>>
>>> 3**2 * np.linalg.det(A) # 3²，乘 A的行列式
-18.0

—— 说明：本文代码基于 python3.0