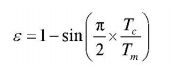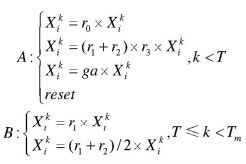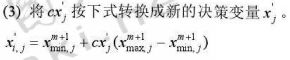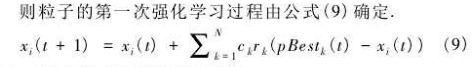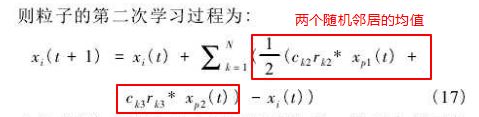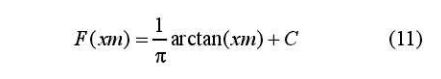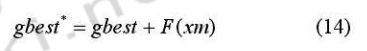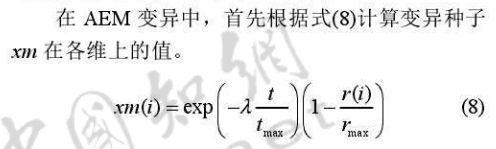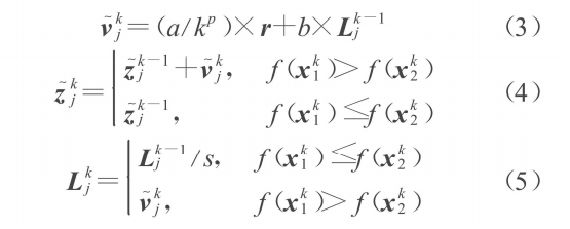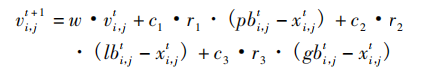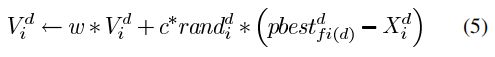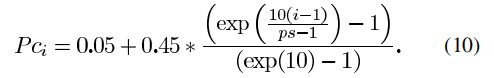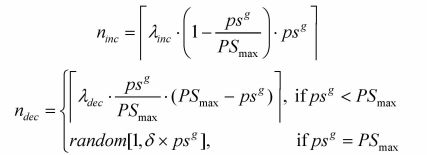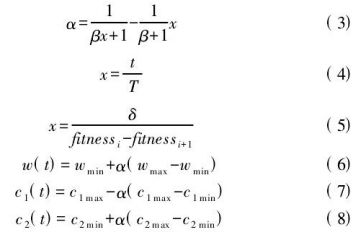PSO算法文献阅读笔记
粒子群算法读书笔记精读
2020《电子信息学报》基于非线性降维的自然计算方法 孙小晴（2020-04-28）
1针对问题
高维大规模优化问题，陷入局部最优与收敛速度和时间复杂度的矛盾。
2创新点
- 非线性降维思想 - NDR
- 将初始化的N个D维个体，视为N行D列的矩阵；
- 求该矩阵的阶梯矩阵，得到列的最大线性无关向量组。（其他列可由最大线性无关向量组表示）
- 引入随机系数，解决降维个体属性参数减少问题
3算法流程
4实验分析
- NDR+PSO与PSO，NDR+GA与GA对比
- 与应用维度策略算法对比
- F8函数的2维图像
- NDR+PSO与PSO仿真时间对比
5个人想法
- 自然计算方向转变
- 其他的人工智能的降维思想拿来利用？！
2019《电子学报》混合均值中心反向学习粒子群算法 孙辉（2020-04-29）
1解决问题
平衡粒子群算法勘探和开发能力（全局搜索和局部搜索）
2创新点
- 贪心选择所有粒子和部分优质粒子的均值中心，得到的==混合均值中心（HMC=min（MC,PMC））==进行局部细致搜索
粒子群体的均值中心MC：所有粒子位置在相同维度的算数平均值，每一维都有一个中心
粒子适应度的均值MVF：所有粒子适应度值的均值
偏均值中心PMC：挑选优于MVF的粒子构成部分优质粒子，在相同维度的算数平均值，每一维都有一个中心
- 同时对混合均值中心进行反向学习，进行全局探索
3算法流程
4实验分析
- 实验分析HMC策略优势，比较MC、PMC、HMC三种均值中心对实验结果的影响
- 实验分析反向学习后收敛情况、聚集程度，得出混合均值中心的反向学习性能提升更大
- 与最新改进的粒子群算法、人工蜂群算法、差分算法对比
- CEC2015测试集
5写作技巧
- 分析中心极限定理和多元正态分布，引出本文混合均值中心
- 实验验证混合均值中心具有更好的求解结果
2019《软件学报》引入多级扰动的混合型粒子群优化算法 徐利锋（2020-04-30）
*粒子群算法（PSO）、标准粒子群算法（SPSO）、带收缩因子的粒子群算法（PSOCF）
1解决问题
粒子群算法易于陷入局部最优问题
2创新点
-
根据迭代深度切换SPSO与PSOCF，中前期：SPSO对解空间的探索好，中后期：PSOCF收敛速度快
-
多级扰动机制：
-
一级扰动：更新粒子位置时，结合SPSO
- 目的是增强粒子对解空间的遍历能力（类似混沌扰动）
- 引入一级扰动取决于概率：概率与最大迭代深度Tm和当前迭代次数Tc有关
随迭代增加，一级扰动概率降低-
怎样扰动？
一级扰动A：优化前期，增大对粒子本身邻域探索能力
一级扰动B：算法后期，对粒子位置小幅探索修正
两种中随机选择一种：
T为中前 后期的切换点，r0=[-2,2]，r123=[0,1]，ga=标准高斯随机数，reset重置粒子位置
-
二级扰动：陷入局部最优时，结合PSOCF
-
判定标准：粒子10次未发生变化
-
怎么扰动？
基于最优位置附近的随机位置分布，跳出局部最优（避免太随机了）
ra=[-2,2], Xgb分别为k-1代的种群最优位置和k+1代的种群最优位置，k陷入局部最优迭代深度
-
-
3算法流程
4实验分析
- 对子问题进行实验分析
- 对算法中设置的随机参数进行实验分析
- 四种维度下的对比实验
5写作技巧
- 算法在何时切换SPSO与PSOCF作为一个子问题，进行分析和实验
- 算法分析充分全面，都有实验支撑，到底是《软件学报》的文章
6个人想法
- 创新点需要分析透彻，不一定是多么好的idea，但是分析和实验要充分全面
2017《系统仿真学报》基于logistic映射的自适应变尺度混沌粒子群算法 曾艳阳（2020-05-06）
1解决问题
2创新点
-
利用logistic映射对粒子群混沌初始化
-
自适应调整参数
-
惯性权重调整策略
所有粒子avg（fitness），pavg为比avg（fitness）好的粒子适应度值的平均值
粒子i适应度值若比pavg好，则赋值小权重
粒子i适应度值若比avg差，则赋值大权重
粒子i位于avg和pavg之间，采用w非线性增长策略
-
学习因子调整策略
前期c1大、c2小，利于全局搜索；后期c1小、c2大，利于收敛到最优解
-
-
以种群适应度值方差判断早熟收敛
-
基于logistic映射的变尺度混沌局部搜索（重点！！！）
在适应度较好的粒子周围局部搜索
-
缩小混沌变量搜索范围
-
将较优粒子初始混沌变量转换成新的混沌变量
-
-
-
3算法流程
4写作技巧
- 虽然实验分析少，但是创新点多，并且特别多的复杂公式。
2019《智能系统学报》基于目标空间分解和连续变异的多目标粒子群算法 钱小宇（2020-05-07）
1解决问题
多目标PSO收敛行和多样性不佳问题
2创新点
- 目标空间分解法
- 粒子的分类和更新
- 差分变异、高斯变异、柯西变异三种变异的连续变异
目前还没看明白！！！（需要静下心来再研究）
2017《IEEE》A Modified Multi-Swarm Optimization with Interchange GBEST and Particle Redistribution-具备互换性Gbest和粒子重新分配的改进多群PSO算法（2020-05-08）
1解决问题
粒子群算法易于陷入局部最优。
- 粒子群算法会捕获一个局部最优点，多种群会捕获多个局部最优点
- 变异
2创新点
-
陷入局部最优时，多个种群内每个粒子都重置Pbest，根据PR（重新定位概率）给粒子位置加扰动，如下式：
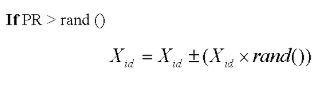
然后重新计算适应度值，更新Pbest i 和Gbest j
（判断陷入局部最优的方法是TR代Gbest未发生更新）
***策略的作用是：***陷入局部最优位置了，增加一个小扰动来重新定位粒子位置
-
陷入局部最优时：
- 如果Gbest i和下一个种群的Gbest i+1相同，则重置Gbest i
- 如果Gbest i 不相同，则将Gbest i+1赋值给Gbest i
***策略作用是：***如果相邻两个种群Gbest相同，重置Gbest有利于种群跳出局部最优
如果相邻两个种群Gbest不同，互换Gbest相当于提供了一个轻微的变异，有利于局部搜索
3算法步骤
4 个人想法
一些实验参数的设置：PR=0.7，TR=100，也并没有对着两个重要参数进行分析说明或者仿真实验！
创新加变异，然后对于陷入局部最优的多个种群互换Gbest来达到种群间通信。
2017《通信学报》无惯性自适应精英变异反向粒子群优化算法 康岚兰（2020-05-09）
1 解决问题
反向粒子群优化算法计算开销大，易于陷入局部最优的不足
- 虽然粒子更新公式中的惯性项保持了粒子多样性，但同时降低了种群收敛速度
2 创新点
-
NIV，一种新的粒子运动方程（目的是相比PSO利用个体经验更多，NIV更多利用种群信息）
-
type1：NIV-D
随机选择种群中2个个体，利用个体间的差异，指导粒子运动
-
type2：NIV-U**（本文采用这种方式（通过实验分析表明这种方式粒子聚集更明显））**
将个体间的相互协作推广到整个种群中，扩大协作的范围
NIV-U与NIV-D相比，通过种群前两个时刻中所有粒子经验来指导当前粒子飞行，收敛速度更快（下文实验证明）。
但以上两种都无法探知所有环境信息，因此粒子仍可能陷入局部最优，所以提出下面的NIV-R
-
type3：NIV-R
将差分项用一个随机值来代替
直观看，过多的随机性对空间的探索比较盲目，但是却使粒子获得跳出局部最优的机会（下文实验证明）
-
-
AEM，自适应精英变异策略（进一步降低陷入局部最优可能）
- 种群迭代初期性能较差，较大的变异值提供足够大的扰动，扩大解空间；但随着迭代，变异值变小，确保平滑收敛到最优值。
- 另一方面，群体极值收敛到很小很小的时候，需要较大的变异值，增强算法搜索能力；当搜索足够充分时，变异值减小可以避免最优值的动荡，从而加快算法收敛速度。
3 算法流程
4 实验分析
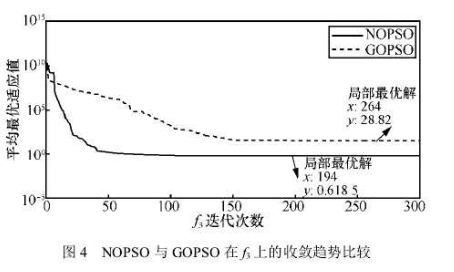
- 收敛趋势比较
- 对不同形式的NIV更新公式分别应用到算法中，进行实验
- 对AEM、GOBL、NIV三种策略分别与PSO结合，进行实验分析
- 对AEM策略参数C在13个测试函数上做实验分析
- 对提出的NIV算式中的学习因子进行Friedman检验，对实验结果进行分析
5 写作技巧
- 有很多看起来效果很好的设想，前文提出来了，后文都有充足的实验分析进行论证，使得通篇文章有理有据。
- 对于创新点分析到位，可以提出一个点的多个版本，在文中详细论述各自的优缺点，实验验证哪个版本最好。
- 对于相同方向的其他优秀文章创新点，单独摘出来和自己的创新点进行实验比较。
- 对于结果不仅仅是有求解结果数据和收敛曲线，还有一些运行结束的迭代次数用箱线图统计、在某些某个函数上的收敛趋势比较、在某些某个函数的性能比较（包括最优、最差、均值、方差）
- 对一些参数的取值，也是用实验的验证去设置，也使得文章更严谨更科学
6 个人想法
- 首先就是这篇文章写得真的很好！文字描述、实验验证都全面而且严谨，有理有据。
- 对于粒子群算法公式的改进方面的好文章
- 精英变异方面可以利用也可以改进
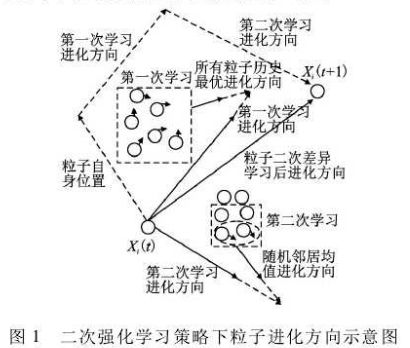
2018《小型微型计算机系统》采用二次强化学习策略的多目标粒子群优化算法（2020-05-14）
1解决问题
针对粒子群算法进化后期出现的早熟收敛、种群多样性低的问题
2创新点
-
无速度MOPSO算法框架提高收敛性，粒子向种群最优粒子的历史最优位置学习，实现粒子第一次学习；
-
基于分解策略，使粒子向指定数量的邻居均值学习，实现粒子第二次学习。
每个粒子都有三重属性向量：粒子当前位置向量、种群最优向量、指定数量邻居均值向量
-
档案维护策略
外部档案用来存放迭代产生的非劣解集
3算法步骤
2016《通信学报》带自适应精英扰动及惯性权重的反向粒子群优化算法 董文永（2020-5-18）
1解决问题
针对反向粒子群优化算法存在的易陷入局部最优，计算开销大等问题
是基于一般性的反向学习基础进行改进
2创新点
- 自适应精英变异策略（AEM）
仅将gbest作为精英粒子，每次迭代根据下式进行自适应变异，若新个体优于原gbest，则替代为新gbest
其中，
- r较小，需要较大变异值F，提高算法搜索能力；r增大时，群体较为分散，变异值F减小，加速算法收敛。
- 迭代初期（t较小），先验认知不足，变异值F增大；随着迭代（t增大），变异值F减小，平滑收敛。
- 算法初期扩大搜素偶空间，迭代后期，变异率逐渐减小，避免震荡同时加速算法收敛。
- 非线性自适应惯性权重更新策略（NIV）
-
粒子适应度值优于平均值，取得最大w，增加粒子活跃度；反之赋予较小w，向优势区域靠拢，
-
同时，favg-fmin较小，（所有粒子趋于一样），w增加；favg-fmin较大，（粒子分散），w减小。
反向学习（OPSO），利用粒子适应度比重等信息，引入NIV，调整各粒子的活跃程度，加速算法收敛；为避免陷入局部最优，提出（AEM）来增大搜索范围，结合反向搜索，跳出局部最优。
3算法流程
4实验分析
-
算法的时间复杂度分析
分析算法的各个主要的策略和步骤。之后写文章来看看这里怎么写的！！！
-
策略有效性分析
加策略的结果，和不加策略的结果对比
-
参数敏感性分析
策略中重要参数取不同值进行对比
2005《计算机学报》广义粒子群优化模型 高海兵
1解决问题
粒子群未能有效解决的离散及组合优化问题（粒子群算法所不擅长的）
2创新点
-
广义粒子群优化模型（GPSO）
通过分析粒子群优化机理，忽略粒子的具体更新策略。
-
利用该模型提出基于遗传操作的粒子群优化模型
GPSO模型中以遗传操作作为粒子更新算子
- 确定算法参数和适应度函数
- 解的编码
- 初始化
- 更新个体极值
- 更新邻域极值
- 粒子与其个体极值交叉
- 粒子与其邻域极值交叉
- 粒子的自身动态变异
- 算法停止条件判断
-
Inver over是针对TSP问题的遗传操作，提出基于Inver over操作的粒子群优化算法
3个人想法
很适合初学入门，对于PSO讲解非常详细，但是粒子群算法不适用于离散问题，所以不建议深究和继续探索。
也是我研究生阶段阅读的第一篇期刊文献，不适用于我们所研究的连续优化问题。
2010《计算机学报》智能单粒子优化算法 纪震
1解决问题
大部分随机优化算法的性能都是随维度的增加而变差
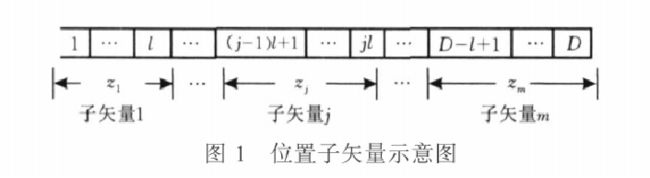
传统的PSO算法往往同时改变整个粒子各个维度上的数值，并根据更新后的解矢量得到一个适应度值。适应度值仅能判断解矢量的整体质量，但不能判断各部分维度是否向最优方向移动
全局最优：[0, 0, 0]
初始解：[1, 1, 1]
随机扰动：[0.2, -0.5, 0.3]
下一代解：[1.2, 0.5, 1.3]
2创新点
-
提出采用一个粒子在解空间搜索
-
粒子的位置矢量被分解成一定数量的子矢量，并基于子矢量对粒子进行更新
-
怎么分解？
对于维之间相关性较大的函数，根据函数特征去决定子矢量的个数（降维！！！）
-
-
-
新的学习策略
前一部分：多样性部分，后一部分：学习部分
如果找到更好的解，粒子下一代的位置就会加上v，同时学习因子L=v；如果没有找到更好的解，就不改变位置，同时令学习因子L=L/s。
其目的是若发现了更好的解，则会将速度中的学习部分×b倍，加速向更优点靠近；如果适应度值没有变好，那么学习因子会缩小s倍。
若迭代很多次适应度值都没有改善，L将以1/s的速度减小，当减小到0，那么粒子只由多样性部分决定粒子速度，那么久容易跳出局部最优。
3算法步骤
4个人想法
一个粒子进行迭代寻优很新颖，同时时间复杂度将大大降低，但是其求解精度一定不会特别好。同时对于维度相关性的确定，不就是降维的思想吗？降维思想可以继续想想！！！
2018《电子学报》基于多种群的自适应迁移PSO算法 邓先礼
1解决问题
标准PSO单一社会学习模式造成的易陷入局部最优和后期收敛速度慢
2创新点
-
扩展社会学习：Pbest、Gbest和Lbest（环形拓扑下邻居最优）
三个种群分配不同加速度因子，赋予种群不同搜索特性
-
周期评估性能，指导粒子迁移
何时粒子迁移呢？
每隔cycle代就进行种群性能评估，执行粒子迁移
如何评估种群性能
gbfinew 表示迁移周期来时新的Gbest，gbfiold 表示迁移周期来前的旧Gbest
avgfinew 表示迁移周期来时所有粒子的最新Pbest的平均值；同理avgfiold
3算法流程
4实验分析
- 实验测试函数选取CEC2013，28个函数
- 显著性检验
- t-检验
- Friedman-检验
5个人想法
- 多种群小生境，寻找种群间的***信息交流机制？！！！***
2016《计算机学报》基于自适应搜索中心的骨干粒子群算法 王东风
骨干粒子群算法BBPSO，取消速度项，粒子位置由服从高斯分布的随机采样获得。
1 解决问题
BBPSO在单峰函数具有很好的效果，但是在多峰函数上表现不好
2 创新点
- 搜索中心自适应调整：基于粒子适应度值，提出对粒子位置高斯采样均值的自适应调整策略。增大
- “镜像墙”越界粒子处理方法：
- 采用不同拓扑结构：算法前期随机结构，增强群体多样性；算法后期全局结构，增强搜索准确性
2006《IEEE》Comprehensive Learning Particle Swarm Optimizer for Global Optimization of Multimodal Functions-用于多峰函数全局优化的综合学习粒子群算法 J.J. Liang
CLPSO
1解决问题
保留种群多样性，防止早熟收敛。
2创新点
-
综合学习策略
Pbestfid是种群随机选取两个粒子，选择较好者的Pbest作为该维度的学习对象。当某个粒子的学习对象是他本身，那么就随机选择一个维度从另外一个粒子的该维度进行学习。
-
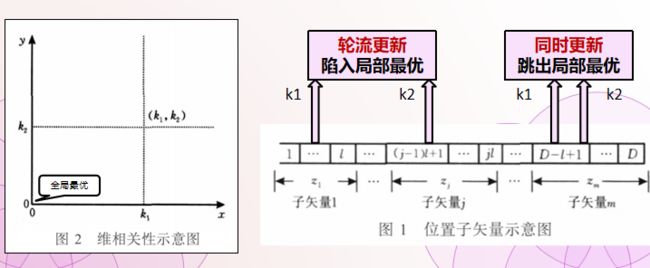
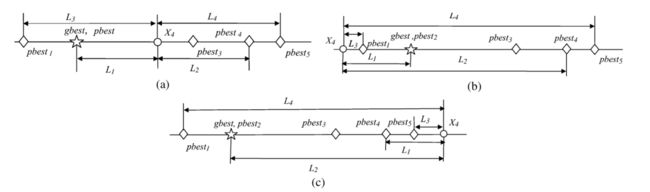
分析CLPSO的搜索行为
- （a）图二维粒子，如果gbest和pbest位于当前粒子的两侧，可能引起粒子震荡，更可能为gbest提供更大的能量，（gbest-X）>（pbest-X），向gbest移动。
- （b）图二维粒子中，如果gbest和pbest位于当前粒子的同一侧，并且gbest在中间，那么会落到gbest，搜索空间减少。
- （c）图，本文CLPSO，如果gbest和pbest位于一侧时，通过学习任意两者较优的pbest，跳出当前位置，搜索空间增大。
-
学习概率Pc
为种群中粒子设置不同的学习概率（0~0.5），使粒子在种群中具有不同水平的勘探和开发能力。
-
搜索范围的设置
常见的边界设置
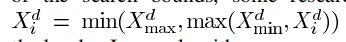，但是本文设置为若粒子在[Xmin,Xmax]之内，才计算适应度值，更新信息。若不在，则不计算，直接进行下一个粒子。 -
刷新间隙
若粒子m代都没有得到改进提升，则分配学习对象。
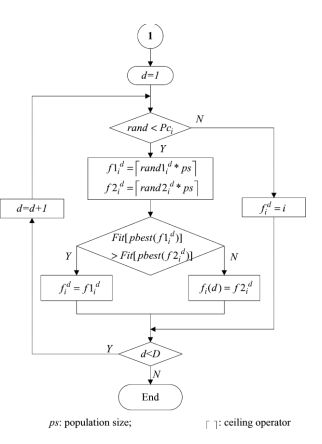
3 算法流程
*2012《软件学报》自适应动态控制种群规模的自然计算方法 王蓉芳
1 解决问题
提出自适应的动态控制种群规模模型，适用于各类自然计算方法
- 本文需解决的问题：（分别对应创新点123）
- 种群规模何时，触发增删操作的条件是？
- 变化多少？增删个体的数目依据什么？
- 如何变化？增删算子如何实现？
2 创新点
-
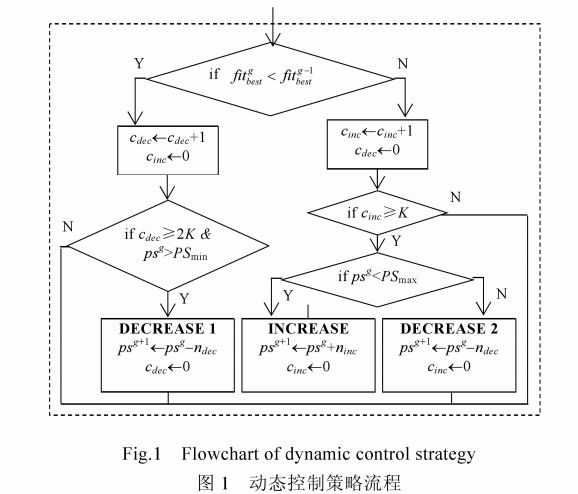
动态控制策略框架，源自于文献【2008《IEEE》Solving large scale global optimization using improved particle swarm optimizer】，文献提出种群管理PM方法，本文就是对该方法的改进，如下：
如果最优个体连续2K代都更新，并且当前种群规模psg>PSmin（种群规模下限），那么触发删除算子1
如果最优个体连续K代都不更新，并且当前种群规模psg>PSmax（种群规模上限），那么触发删除算子2
如果最优个体连续K代都不更新，并且当前种群规模psg>PSmax，那么触发增加算子
-
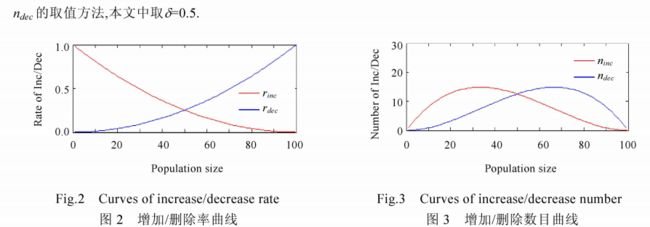
基于logistic模型的增加/删除数目自适应变化的方法
增加/删除个体的数目决定了种群规模psg的变化幅度，psg较大时，应增加数目减少，删除数目增大，反之相反。
此处改进了logistic人口模型，设计增加/删除多少个粒子？
-
增加/删除算子设计
-
增加算子：有效性（新增加的粒子位于较好的位置）、多样性（增加的粒子是没有经过为位置）
-
删除算子
- 最优个体连续2K代都更新，为减少时间复杂度，采用分组最差删除方法，即除最优个体外的psg-1个个体按适应度值排序，随机分成ndec个组，删除每组最差的个体。
- 种群最优连续K代都不更新，陷入局部最优，相似个体增多，多样性变差，本来应该增加个体来跳出局部最优，但是种群规模超过上界，删除种群中适应度较差的ndec个个体。
-
3 算法流程
*4 写作技巧
算法时间复杂度的分析
很多好文章都有时间复杂度的分析，即每次迭代所需时间的有哪些部分。
5 实验分析
- 对于删除多少个粒子中的参数，进行了实验分析：
- 将该框架应用于差分进化算法（DE）和粒子群算法（PSO）
6 个人想法
该文章的确写的非常好，写作结构特别新颖，分析也十分到位，利用其它的好思想进行改进应用于自然计算方法，得到好的效果。
以后往自然计算方向写文章。
2015《计算机学报》具备反向学习和局部学习能力的粒子群算法 夏文学
1解决问题
粒子群算法种群多样性和收敛性之间的矛盾
2创新点
-
种群历史最优位置邻域的局部搜索
利用迭代飞行后的种群最优Pg1和种群次优Pg2之间的差分结果指导Pg1进行局部搜索。
r为[-1,1]之间的随机数，用来控制局部搜索的方向，dt为线性递减的局部缩放因子d=d*（1-t/T）
-
反向学习
陷入局部最优，n个粒子进行S代反向学习，其他N-n个粒子学习方式不变，反向学习对象是该粒子的历史最差位置，以及初始选择规模m的初始最差种群中的任一个体，为了保证反向学习广泛的分布在搜索区域，这m个个体应该具有较大的欧氏距离，两两距离大于排异半径R。
- 反向学习期间对粒子飞行速度动态调整
3算法流程
4实验分析
时间复杂度分析
反向学习机制分析
*2013《电子学报》一种基于动态边界的粒子群优化算法 李迎秋
1解决问题
根据停滞期粒子运动特点，动态调整搜索边界，引导粒子到更有效的区域搜索，减轻早熟收敛
2创新点
-
边界的动态调整
D维搜索空间相当于一个D维盒子，所有粒子在[Bl,Br]D内飞行时，就收缩边界；否则就扩展边界。
上述操作是必须边界与全局极值距离大于阈值时才进行。
如果过度收缩，即边界与全局极值距离小于等于阈值，需要对搜索空间的边界进行重置，以扩大搜索范围。
cb：收缩率；cb’=1-cb；ob：扩展率
- *停滞粒子的处理
- 停滞粒子飞行速度为0，加入正态分布的随机数来激活粒子；
- 清除粒子的个体经验，即粒子个体极值设置为当前位置
- 并不是对所有粒子都施加变异操作，根据大于阈值0.9的随机数选择少部分粒子施加变异操作。
*2004《电子学报》自适应变异的粒子群优化算法 吕振肃
1解决问题
增加跳出局部最优的能力
-
前提分析
粒子群算法不管是全局收敛还是早熟收敛，种群中粒子都会聚集，根据函数特点要么收敛于一点，要么收敛于多点。
-
群体适应度方差
反应种群内粒子的收敛程度！！！值越大越收敛，反之处于随机搜索阶段。
-
粒子全局收敛？早熟收敛？
种群最优=理论全局最优，就是全局收敛
2创新点
如果改变全局极值gbest（变异操作），就可以改变粒子前进方向，从而让粒子进入其他区域搜索，就有发现更优解的机会了。
-
满足变异条件的gbest按一定概率pm变异
k取[0.1-0.3]内的任意数
如何变异呢？
3算法步骤
2004《计算机科学》混沌粒子群优化算法 高鹰
1创新点
- 混沌寻优思想引入粒子群优化算法
logistic混沌系统
Zn+1 = uZn（1-Zn）n=0,1,2…
u为控制参数，一般取u=4，系统处于混沌状态。
2算法步骤
3个人想法
混沌运动具有随机性、遍历性、规律性等
对于种群初始化利用混沌特性，得到的解具有较好的初始状态。
2018《小型微型计算机系统》一种带有二维扰动和自适应学习因子的粒子群算法 王磊
1解决问题
粒子群算法易于陷入局部最优，后期收敛速度慢和收敛精度低。
2创新点
-
自适应惯性权重和学习因子
为了平衡全局搜索能力和局部搜索能力，迭代初期，w应该具有很快的下降速度；迭代后期，w应该具有较慢的下降速度
-
基于位置、速度二维扰动更新粒子信息
对周期性震荡的正弦函数因子进行改进，原来的方法有两个缺点：
1如果全局最优已经在最优解的附近，扰动会偏离最优解；2震荡后的位置与原位置更远
对于第一个问题，限定为只有陷入局部最优的粒子才进行震荡；第二个问题，将震荡幅度限制为20%之内。
-
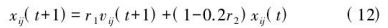
变异一些较差粒子
所有粒子都向全局最优学习，会导致种群多样性变差，为解决这一问题，每次迭代选取一定数量适应度最差的粒子进行随机变异，这样会增加种群多样性。（2/8原则）
3算法流程
4个人想法
这篇文章前面的理论叙述和分析十分全面，后面的实验结果分析就比较简单。
2020《小型微型计算机系统》一种最优粒子逐维变异的粒子群优化算法
1解决问题
针对粒子群算法容易陷入局部最优/收敛速度过慢/精度低等问题
2创新点
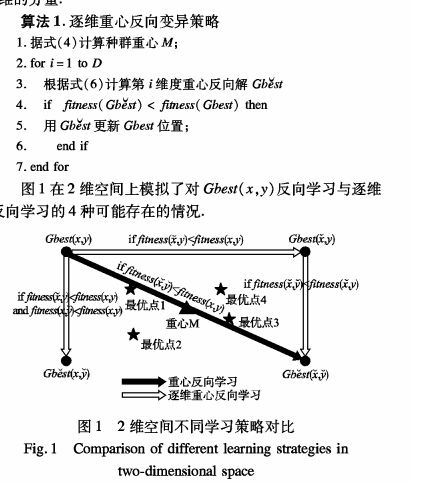
提出一种新的逐维变异策略，对全局最优粒子进行逐维的重心反向学习变异
逐维变异降低了维度间干扰，通过更新最优位置引导粒子向更好的位置飞行，加强了种群多样性。
3算法流程
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-w6ueSVyh-1602137960842)(C:\Users\16222\AppData\Roaming\Typora\typora-user-images\1591984593812.png)]
2015《Swarm and Evolutionary Computation》Heterogeneous comprehensive learning particle swarm optimization with enhanced exploration and exploitation-改进探索与开发的异构综合学习粒子群算法
本文提出了一种综合的学习粒子群优化算法，该算法具有更强的探索性和开发性，被称为“异构综合学习粒子群优化”（HCLPSO）。在该算法中，群体人口被分为两个亚群。每个子种群都被分配为仅专注于勘探或开发。综合学习（CL）策略用于生成两个子群体的样本。在勘探亚群中，示例是通过使用勘探亚群本身中粒子的个人最佳体验而生成的。在开发子种群中，将整个种群的个人最佳经验用于生成样本。由于勘探子种群无法从开采子种群中的任何颗粒中学习，因此即使开采子种群过早收敛，也可以保留勘探子种群中的多样性。在转移和旋转基准问题上测试了异构的综合学习粒子群优化算法，并与其他最新的粒子群优化算法进行了比较，以证明该算法优于其他粒子群优化变体。
2005《Journal of Information Science and Engineering》A Parallel Particle Swarm Optimization Algorithm with Communication Strategies-具有通信策略的并行粒子群优化算法
1解决问题
种群间粒子之间的通信问题
2创新点
提出了粒子群优化（PPSO）算法的并行版本以及可以根据数据的独立性使用的三种通信策略。
- 第一个策略是为独立的或仅松散相关的解决方案参数设计的，例如 Rosenbrock 和 Rastrigrin函数
- 第二种通信策略可以应用于更紧密相关的参数，例如 Griewank 函数。
- 在参数的属性未知的情况下，可以使用第三种混合通信策略。
3算法流程
2002《IEEE》Population Structure and Particle Swarm Performance -种群结构和粒子群性能
1解决问题
系统研究了各种种群拓扑对粒子群算法的影响。生成了符合规格的随机图，并比较了它们在几个标准上的性能。是什么构成良好的人口结构？
2创新点
主要对种群间的拓扑结构进行分析
我们将粒子群中的影响概念化为流动信息，该信息在相互连接的个体对之间移动最快，但是由于中介的存在而受到缓冲或减慢。因此，如果个体 i找到一个好的解决方案，则可以将其传递给其相邻的邻居 j，但不能立即传递给未与 i 连接的 k。但是，如果该解决方案确实是一个好的解决方案，则j 的性能将会提高，直到 j（连接到 k）在 k 的邻域中达到最佳。发生这种情况时，i 最初找到的解可能会传达给 k。
1999《IEEE》Small Worlds and Mega-Minds: Effects of Neighborhood Topology on Particle Swarm Performance-小世界和大思想：邻居拓扑对粒子群性能的影响
1解决问题
种群间粒子的拓扑结构
2创新点
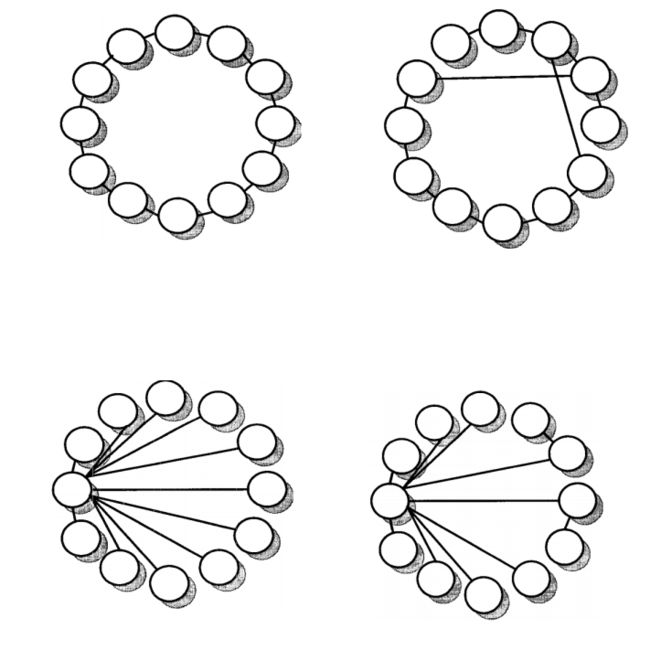
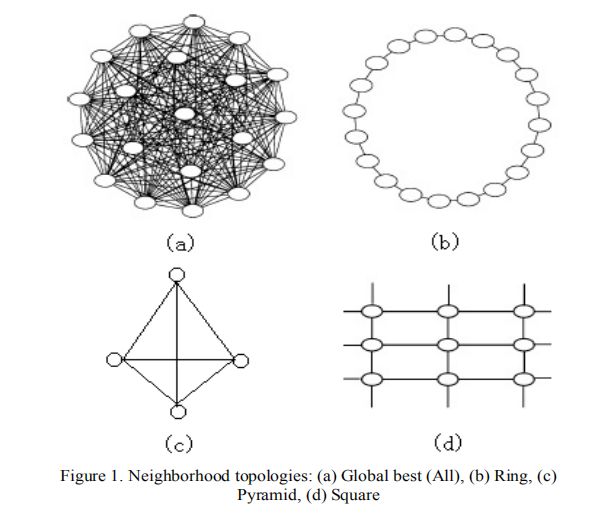
• 圆（/最佳）：每个人仅与其 K 个直接邻居相连
• 轮子：一个人连接到所有其他人，而他们只连接到另一个
• 星号（最棒）：每个人都与其他每个人联系在一起，并且
• 随机边：对于 N 个粒子，在成对的个人之间分配了 N 个随机对称连接。
2004《IEEE》Particle Swarm (Optimization Algorithms with Novel ]Learning Strategies- 新型学习策略的粒子群优化算法
1解决问题
粒子群算法在多峰函数上的不足
2创新点
提出了三种具有新颖学习策略的
- 精英学习
在 PSO 中，最佳位置gbest 可能具有有用的信息。在 ELPSO 中，群中的精英，最优秀的人才和最优秀的粒子被用作典范。为了充分利用精英，对于每个粒子，随机选择 m 个维（或变量）以从 gbest 学习，而其他维从 pbest 学 习。m 是整数。如果 m 过大，则当 gbest 落入局部最优值时，它将使其他粒子更快地吸引到局部最优值， 并且会由于实验结果而过早收敛。相反，当 m 较小时，粒子在初始代中保持较大的多样性，并且更有可能脱离局部最优。
- 自身学习
认为群体中的每个粒子都有其良好的特性，其他粒子可以学习这些特性。因此，在此版本中，粒子自身的最佳和其他粒子的最佳用作示例。因此，每个粒子都可能从群中的所有粒子中学习。在搜索过程中，我们不知道每个粒子的尺寸是好是坏。因此，粒子的每个维度都有被其他粒子学习的平等机会。对于每个粒子，其他粒子的最佳尺寸是随机的根据概率选择。
- 他人学习
基于对其他两个版本的分 析，我们提出了 CLPSO，该 CLPSO 从群体的最佳，粒子的最佳和其他粒子的最佳学习中学习，以便粒子从精英，自身和其他粒子。在此版本中，将随机 选择 m 个维度以从 gbest 中学习。随机选择一些剩 余的 Dm 维以从一些随机选择的粒子的最佳学习中 学习，而其余的维则从其最佳学习中学习。当 m = -0 时，尽管 gbest 似乎毫无用处，但实际上它是一个粒子的 pbest，并且被其他粒子学习的机会均等。
2016《Swarm and Evolutionary Computation》Directionally Driven Self-Regulating Particle Swarm Optimization algorithm-定向驱动自调节粒子群算法
1解决问题
改进基本 SRPSO 算法
2创新点
定向驱动自调节粒子群优化（DD-SRPSO）算法。在 DD-SRPSO 中，我们合并了两个新策略，即定向更新策略和旋转不变策略。与 SRPSO 中一样，DD-SRPSO 中的最佳粒子使用相同的自调节惯性权重更新策略。性能不佳的粒子被分组在一起，以从精英粒子组中获得方向更新。随机选择所有剩余的粒子，以进行全局搜索方向自我感知的 SRPSO 策略或旋转不变策略，以探索搜索空间的旋转方差性质。
3个人想法
写的很不错，还没有十分读懂，之后还要继续多读几遍！！！
2020《计算机应用研究》一种新的自适应动态文化粒子群优化算法
1解决问题
克服粒子群优化算法在解决复杂问题时候的难题
2创新点
引入评价粒子群早熟收敛程度判断粒子群状态，算法陷入局部最优，自适应的利用影响函数对种群空间进行变异更新，从而有效发挥文化粒子的双演化双促进机制，并且根据收敛成都自适应调整惯性权重。
3算法流程
2017《IEEE》Particle Swarm Optimization with Selective Multiple Inertia Weights-选择性多重惯性权重的粒子群优化
在过去的几十年中，粒子群算法被广泛用作单峰，多峰，可分离和不可分离的优化问题的优化方法。PSO的流行变体是PSO-W（惯性重量PSO）。尝试用选择性多重惯性权重（SMIWPSO）修改PSO，以增强PSO的搜索能力。本文用四种最佳选择的惯性权重技术实现了SMIWPSO，即线性减小惯性权重，混沌惯性权重，随机惯性权重和恒定惯性权重。考虑惯性权重的选择取决于控制参数P的协议。针对25个标准优化问题，针对PSO检查SMIWPSO性能。实验结果表明，SMIWPSO在效率，可靠性和鲁棒性方面有显着改善。
2017《IEEE》Particle Swarm Optimization and Cuckoo Search Paralleled Algorithm-粒子群算法与布谷鸟搜索并行算法
1创新点
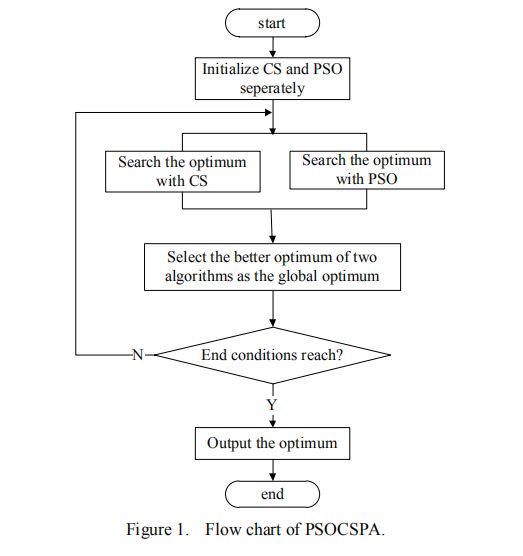
抽象粒子群优化算法与杜鹃搜索算法都是仿生群优化算法。算法简单方便。他们已经适用于许多领域。然而，这些算法有明显的优势缺点。当它们应用于复杂的优化问题，他们不能获得最优解，所以有些必须采取措施，以改善其全球性搜索能力。本文提出了粒子群优化算法算法和布谷鸟搜索算法并行进化。在一代的末期，两者中较好的解决方案选择算法作为全局最优解。
2算法流程
2016《IEEE》An Opposition-Based Learning Competitive Particle Swarm Optimizer-基于对立的学习竞争粒子群优化器
1创新点
提出了一种基于对立的学习竞争粒子群优化器（OBL-CPSO），以解决PSO中过早收敛的问题。OBL-CPSO中采用了两种学习机制，分别是来自竞争群优化器（CSO）的竞争学习和基于对立的学习。在OBL-CPSO的每次迭代中，竞争性学习都在来自群体的三个随机选择的粒子之间进行，然后进行适合度的比较。具有最佳适应性的粒子（称为获胜者）直接传递到下一个迭代。适应性最差的粒子向获胜者学习，中等适应性的粒子通过基于对立的学习来快速利用搜索空间，然后将它们以更新的位置和速度传递到下一次迭代。
2算法流程
2015《IEEE》Small World Network Based Dynamic Topology for Particle Swarm Optimization-基于小型世界网络的动态拓扑用于粒子群优化
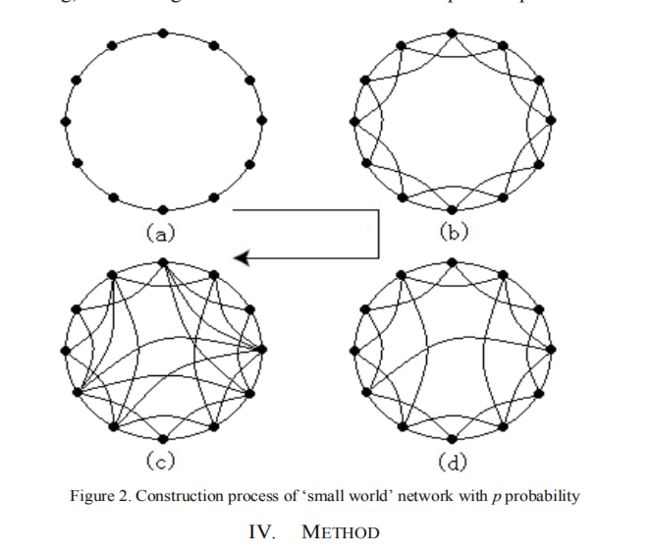
提出了一种基于“小世界”网络的动态拓扑粒子优化算法。该技术通过动态更新粒子群优化算法的邻域拓扑来模仿“小世界网络”中的信息传播。提出的动态邻域策略可以有效地协调粒子群优化算法的探索和利用能力。仿真表明，群体收敛是有保证的。实验表明，该方法保持了种群多样性，增强了全局搜索能力。
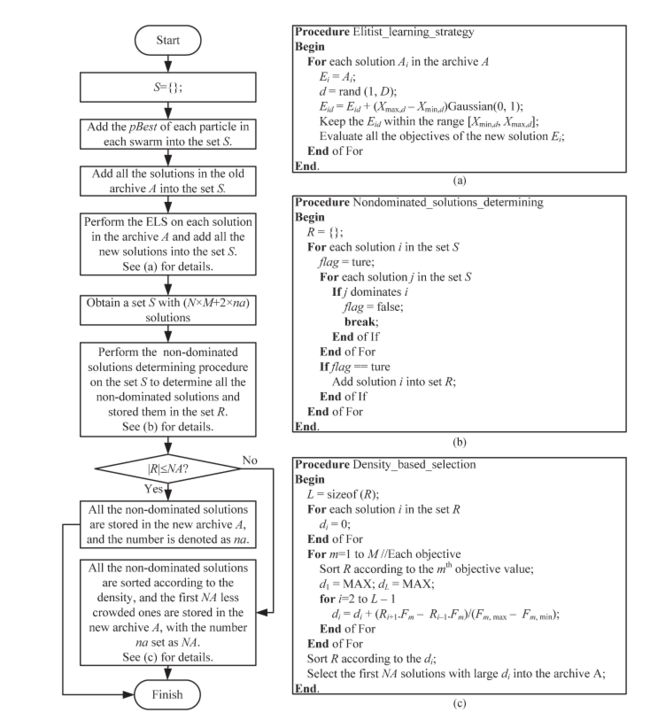
2013《IEEE》Multiple Populations for Multiple Objectives:A Coevolutionary Technique for Solving Multiobjective Optimization Problems-多目标的多个种群：解决多目标优化问题的协同进化技术
1解决问题
传统的多目标进化算法（MOEA）在解决多目标优化问题（MOP）时会整体考虑多个目标。但是，由于不同的目标经常相互冲突，因此这种考虑可能会给将适合性分配给个人造成困难。
2创新点
提出了一种新颖的协同进化技术，在开发MOEA时将其称为多目标多种群（MPMO）。MPMO的新颖之处在于，它通过让每个人口仅对应一个目标来提供一种简单直接的方法来解决MOP。这样，可以解决适应度分配问题，因为可以通过相应的目标分配每个人群中的个体适应度。MPMO是一种通用技术，每个人口都可以使用现有的优化算法。本文针对每个种群采用粒子群优化算法（PSO），并基于MPMO技术开发了协同进化的多群PSO算法（CMPSO）。此外，CMPSO是新颖且有效的，它通过使用针对不同人群的外部共享档案库来交换搜索信息，并使用两种新颖的设计来提高性能。一种设计是修改速度更新方程，以使用由不同总体找到的搜索信息来快速近似整个帕累托前沿（PF）。另一种设计是对档案更新使用精英学习策略，以引入多样性以避免本地PF。
3算法流程
2010《IEEE》Particle Swarm Optimization based on self-organizing topology driven by fitness -基于适应性驱动的自组织拓扑的粒子群优化
为了探究动态网络的拓扑特征与粒子群优化（PSO）算法性能之间的关系，将PSO总体视为一个网络，其中每个粒子都表示为一个节点，并且网络结构随着粒子的适应性而动态变化。不同。此外，在本文中，结构更改涉及添加和删除链接，但网络大小保持不变。然后，进行两种模拟。一种针对PSO的结果表明，动态网络能够平衡勘探与开发，因此只要适当选择权重θ，就可以提高PSO的性能。并且网络结构发生变化。随着粒子适合度的变化而动态变化。而且在这方面呢文件中，结构变化涉及添加和删除链路，但网络大小保持不变。
粒子群算法读书笔记泛读
2020《深圳大学学报理工版》基于正态分布衰减惯性权重的粒子群优化算法
1解决问题
针对粒子群算法早熟收敛与收敛速度的矛盾
2创新点
提出基于正太分布分布衰减惯性权重的粒子群优化算法
2015《小型微型计算机系统》基于不同学习模型的精英反向学习粒子群优化算法 赵嘉
2011《计算机学报》基于空间缩放和吸引子的粒子群优化算法_迟玉红
为解决粒子群优化(Particle Swa rm Optimiza tion , PSO)算法中粒子越界、算法进化后期收敛速度慢和早熟收敛的问题, 通过分析 PSO 算法中粒子运动行为和算法稳定性, 提出了一种基于空间缩放和吸引子的粒子群优化(PSOwith sea rch space zoomed facto r and att ractor , SzAPSO)算法.该算法利用对搜索空间进行缩放的边界变 异策略有效控制了粒子搜索范围, 保证了算法全局探测能力;算法中吸引子的引入增加了感兴趣区域的粒子密度, 提高了算法局部开发能力.实验结果表明, SzAPSO 算法收敛速度快、精度高, 且具有较好的鲁棒性.
2013《电子学报》一种基于动态边界的粒子群优化算法-李迎秋
2007 年提出的标准粒子群优化算法(PSO-2007)在进化的后期容易出现停滞现象而导致早熟收敛, 为此本文提出了一种基于动态边界的粒子群优化算法(DBPSO).该算法根据停滞期粒子运动的特点, 将边界动态调整策略引入到PSO-2007 中, 通过跟踪粒子飞行位置的分布动态调整搜索空间的边界, 引导粒子在更有效的区域内进行搜索,从而减轻早熟收敛, 提高收敛精度.典型测试函数的求解实验结果表明 DBPSO 是可行而有效的.
2013《计算机工程与应用》层次环形拓扑结构的动态粒子群算法
粒子群算法（PSO）的拓扑结构决定粒子之间的信息交互方式，是影响算法性能的关键因素。为提高算法性能，提 出了一种层次环形拓扑结构的动态粒子群算法（HRPSO），粒子组成的环被分配在规则树中，算法运行时，环层次中动态 移动。通过 6个标准测试函数优化，比较了 HRPSO与几种基准算法的性能，实验结果证明 HRPSO在精确性和稳定性上具有优势。
2019《IEEE》Center Particle Swarm Optimization Algorithm-中心粒子群优化算法
2018（自动化学报）基于变换函数与填充函数的模糊粒子群优化算法
2020(计算机应用)一种新的自适应动态文化粒子群优化算法
2019（自动化学报）基于相似历史信息迁移学习的进化优化框架
2017（计算机研究与发展）基于网格排序的多目标粒子群优化算法
2017（电子与信息学报）平面框架方向图优化的改进PSO算法
2015《IEEE》A New Particle Swarm Algorithm By Modifying Its Toplogy Structure-通过修改其拓扑结构的新粒子群算法
PSO（粒子群优化）是处理复杂优化的最有效方法之一，在本文中，通过引入改进的拓扑结构来解决新的PSO算法。首先，提出了在有效搜索区域进行PSO粒子探测的规则。然后，介绍了一种新的基于改进链拓扑的PSO算法，称为PSOC（基于改进链结构的粒子群算法）。在PSOC中，粒子仅受其相邻粒子的影响，并且邻域最优在整个总体中不共享。进行数据实验以及与基准上其他流行的改进PSO算法的比较。实验结果表明，PSOC具有较好的全局搜索能力和稳定的优化能力
2012（软件学报）一种多尺度协同变异的粒子群优化算法 陶新民
为了改善粒子群算法易早熟收敛、精度低等缺点,提出一种多尺度协同变异的粒子群优化算法,并证明了该算法以概率1收敛到全局最优解.算法采用多尺度高斯变异机制实现局部解逃逸.在算法初期阶段,利用大尺度变异及均匀变异算子实现全局最优解空间的快速定位;随着适应值的提升,变异尺度随之降低;最终在算法后期阶段,利用小尺度变异算子完成局部精确解空间的搜索.