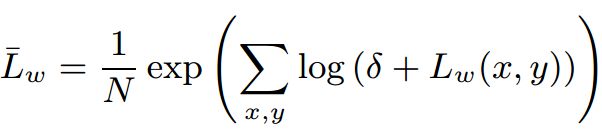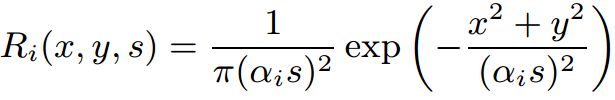HDR技术讲解之Photographic Tone Reproduction for Digital Images论文算法复现及改进
2020/10/14说明：因该博客前后做了几次修改影响了可读性，故而对其进行了重新整理。原博客中还有一个问题，就是论文中初始亮度映射公式写错了，但我没有注意到这一点，并且还把这个公式看错了以致给出了错误的实现程序。当然啦，原博客中给出的改进版程序是没问题的。下面重新贴出程序代码及数据集、测试结果的网盘链接供大家测试。
链接：https://pan.baidu.com/s/1z4RTwJWPexossnhUrNszZQ 提取码：ablb
上一篇文章给大家介绍了基于多尺度对比度调制重组的HDR技术，今天为大家介绍一个更有趣的HDR算法。该算法借鉴了具有150年历史的摄影处理经验，即“遮蔽”与“燃烧”技术。这是种具有悠久历史的印刷技术，在显影过程中，对于过亮的区域就遮一遮光线(遮蔽)，对暗的区域就添加一些光进来(燃烧)。原理很简单，但是怎么利用起来就是个技术活儿了。Erik Reinhard等人的做法是对于每一个像素点都考察不同尺度的邻域，以找到使得对比度没有明显突变的最大邻域。如下面示意图所示，尺度过小和过大时，中心区域和环绕区域间的对比度都比较低，而在正确的尺度上，中心区域与环绕区域的对比度就比较大。不同尺度的运用其实是通过使用不同尺度的高斯滤波器对图像滤波来实现的，中心区域与环绕区域也是半径具有一定比例的两个邻域。记中心区域的尺度为s1,环绕区域的对比度为s2，对于每个像素点，比较两个尺度下的滤波结果V1和V2，设置一个可以利用正确尺度下V1和V2的高对比度性质的公式进行尺度甄选即可。在这之前要做一些预处理。
首先，像很多摄影技术所做的那样，要将一个参考亮度映射到中性灰。作者所采用的参考亮度就是log域均值再取指数的结果：
注意，这一点论文有误，给错写成了
关于这一点，可从Reinchard的另一篇论文 “Parameter Estimation for Photographic Tone Reproduction”(该论文讨论了局部映射函数中key值的自动选取和全局映射函数中Lwhite参数的自动选取技术。该部分内容简单易懂，请读者自行查看论文理解，我就不再单独开一篇博客介绍了)中得到印证。其中，
是一个小的偏移量，以避免出现对数项里出现0值的情况，
是场景的真实照度（“World” Luminance）， 可以简单地认为伽马校正前的像素亮度值是随光照线性变换的，故有：L = 0.27R +0.67G + 0.06B。这个L即可认为是场景的真实照度。
之后是对场景照度进行一个伸缩变换：
其中,a为中性灰参考值，也叫key值，默认为0.18，即所谓的十八度灰。但是这里最大照度值并不一定映射到1，所以a值并没有严格的取值限定，a的取值也可以大于1。需要注意的是，这里的可是没有取对数前的结果，这一点千万不要搞错。另外，为了避免取对数后出现负值导致均值为负的情况，我的程序实现中设定=1。这一点是与论文不同的。
在进行伸缩变换后就可以进行多尺度高斯滤波了。高斯滤波器为：
其中，
的
有1和2两个取值，分别对应中心区域与环绕区域的尺度缩放系数，取值为
,
。具体解释见论文。对应的滤波结果为：
在实现中可以使用FFT进行加速计算。
中心区域和环绕区域各有8个尺度。下一个尺度的中心区域半径等于上一个尺度环绕区域的半径，故而实际上中心区域和环绕区域的尺度加起来只有9个尺度，以1.6的倍率从从1变化到43。
在获得了每个尺度的
和
后，根据中心环绕函数计算一个对比度指标：
其中
默认取值为8.0。分母中前面这一项是为了防止V1趋于0时V取值过大。从最低尺度出发，我们找出满足以下阈值条件
的第一个尺度
（这个部分论文中写错了，应该是大于号，论文中却是小于号，这是个很明显的低级错误）。其中，
是阈值对比度。使用该尺度下的 用下式进行自适应的“遮蔽”和“燃烧”（见论文解释，要参照着论文中的公式(3)去理解，用V1替换成L所带来的对比度改变也是在(3)式本身具有的对比度拉伸和压缩的基础上所做的改变，而不是相对于原始照度L）：
最后，照例贴出我个人实现的matlab程序与处理结果（程序给出了频域滤波和空域滤波两种实现方式。频域滤波需要dipum_toolbox_2.0.1工具箱，就是冈萨雷斯教材附带的那个）：
%% HDR算法复现
% based on the tone mapping technology as described in Erik Reinhard,,Michael Stark,
% Peter Shirley, James Ferwerda, “Photographic Tone Reproduction for Digital Images”
% ACM, 2002
% author: Zhuangzhuang Zhang
% original:2020/09/10
% modified:2020/10/09
% Attention: dipum_toolbox_2.0.1 is needed
close all;clc
filename = 'data/HDR images/Sardbeach.hdr';
try
hdr = double(hdrread(filename));
catch
disp('Can not open file!');
return;
end
if max(size(hdr))>1500
hdr=imresize(hdr,0.5);
hdr(hdr<0)=0;
end
gamma=1/1.6;
picNum=8;
ratio=1.6;
%ratio=1.3;
a=0.36; %用户设置的中性灰
refV=1.0;
phi=8.0;
eps=0.05;
alpha=1/sqrt(8);
figure,imshow(hdr.^gamma);
imwrite(hdr.^gamma,'原始HDR图像.png');
%% 预处理，log域均值取指数结果映射到中性灰
L = 0.27*hdr(:,:,1) + 0.67*hdr(:,:,2) + 0.06*hdr(:,:,3) + 1e-6; %论文推荐的world luminance计算公式,小偏移量为避免被0除的情况
R = hdr(:,:,1) ./ L;
G = hdr(:,:,2) ./ L;
B = hdr(:,:,3) ./ L;
% maxL=max(L(:));
% settedMaxL=20;
% thL=10;
% mask=L>thL;
% settedMaxL=min(maxL,settedMaxL);
% L(mask)=(settedMaxL-thL)*(L(mask)-thL)/(maxL-thL)+thL;%高曝光部分压缩动态范围
LL=log(L+10^-9);
temp=exp(mean(LL(:))); %实践中发现将对数均值再反对数变换（取指数）结果映射到key值，通常可以得到更好的效果（主要是大区域之间的对比度更加合理而不会过低）
L=L*a/temp;
figure,imshow(L);
imwrite(L,'初始亮度映射结果.png');
%% 核心部分：多尺度FFT滤波、不引起对比度突变的最大尺度选择及亮度变换
V1=zeros([size(L),picNum+1]); % V2的当前尺度与V1的下一尺度相同
%----------------------频域实现------------------------------%
% tic
% PQ=paddedsize(size(L));
% for i=1:picNum+1 % picNum+1个尺度，以ratio为倍数递增
% s=ratio^(i-1);
% d=sqrt(PQ(1)*PQ(2))/(sqrt(2)*pi*alpha*s); %为使用lpfilter直接在频域生成滤波器所做的变换，注意lpfilter中指数的分母部分是2*d^2而非d^2
% H=lpfilter('gaussian',PQ(1),PQ(2),d);
% figure,imshow(H./max(H(:)));
% fL=abs(dftfilt(L,H,'original'));
% figure,imshow(fL);
% V1(:,:,i)=fL;
% end
% toc
%-----------------------空域实现-------------------------------%
tic
for i=1:picNum+1 % picNum+1个尺度，以ratio为倍数递增
s=ratio^(i-1);
sigma=alpha*s;
kernelRadius = ceil(2*sigma);
kernelSize = 2*kernelRadius+1;
gaussKernelHorizontal = fspecial('gaussian', [kernelSize 1], sigma);
temp= conv2(L, gaussKernelHorizontal, 'same');
gaussKernelVertical = fspecial('gaussian', [1 kernelSize], sigma);
V1(:,:,i)= conv2(temp, gaussKernelVertical, 'same');
end
V=zeros([size(L),picNum]);
for i=1:picNum
s=ratio^(i-1);
V(:,:,i)=abs(V1(:,:,i+1)-V1(:,:,i))./(a*2^phi/s^2+V1(:,:,i));
end
Vsm=V1(:,:,picNum); %给Vsm初始化，作为8个尺度都不满足条件下的预设值
for i=1:size(L,1)
for j=1:size(L,2)
for k=1:picNum
if V(i,j,k)>eps
Vsm(i,j)=V1(i,j,k);
break;
end
end
end
end
toc
figure,imshow(Vsm);
imwrite(Vsm,'各点参考值图像.png');
Ld=L./(refV+Vsm);
Ld(Ld>1)=1;
figure,imshow(Ld);
imwrite(Ld,'亮度通道重映射结果.png');
%% 色彩还原
rgb=zeros(size(L,1),size(L,2),3);
rgb(:,:,1)=Ld.*R;
rgb(:,:,2)=Ld.*G;
rgb(:,:,3)=Ld.*B;
rgb=rgb.^gamma;
figure,imshow(rgb);
imwrite(rgb,'色彩还原最终结果.png');调试输入：（输入为HDR图像，动态范围很大，显示范围有限不能完全反反映像素点亮度的浮动范围）：
场景亮度图像进行初始映射后：
每个参考点对应（不显著改变对比度）最大尺度的V1图像：
“遮蔽”和“燃烧”处理后:
色彩恢复后的最终结果：
频域处理中间某尺度FFT滤波器及高斯滤波结果示例：
前面就是原始的Reinhard局部色调映射算法实现。看起来还不错是不？然而，问题并没有就此了结，当我们测试更多的图片，尤其是那些动态范围很大的图像，就会发现原始算法的不足之处。第一个问题是光晕效应。如对下面的测试图像：
其处理结果为：
其局部放大为：
再比如对于下面的图像：
其处理后结果为：
局部放大为：
类似的情形还有很多。 这是因为环绕区域与中心区域的比值过大，或者说比例尺太大，导致强边缘附近的像素点选择的尺度差距过大，参考值不连续性太强，从而在映射后的亮度值也出现了不连续的现象。比如对前面两张测试图像，他们对应的各点参考值Vsm图像分别如下：
我们只需要适当地缩小尺度比例即可。实践表明，能使光晕效应基本完全消除的该比例上限约为1.3。我们将该比例改为1.3再重新进行试验，对应Vsm图像分别为：
色调映射的结果为：
可以看出，原来的层状光晕基本得到完全消除。
原始算法的第二个问题就是可能会造成令人不快的亮度反转，尤其是在高曝光区域内的亮度反转。
比如下面这个例子：
把它缩放以查看过亮部分的细节，得到：
用之前的程序处理后得到的结果是这样的：
可以看到夕阳中心区域出现了明显的违反直觉同时又观感不佳的亮度反转现象，而夕阳在海面上的余晖经处理后所造成的亮度反转则更加惹人讨厌。出现这种现象的原因是过亮区域的亮度变化过于剧烈，而尺度的选取又是离散而非连续的，且受计算效率的限制尺度采样率不能太高，因此容易出现过亮区域中某些相对较暗的像素点因为选择的邻域包含了亮区中心部分而使参考值过高从而导致被抑制得太过分，而邻域里亮度相当甚至更暗的像素点却因为选到的尺度更合适、参考值更恰当从而处理后亮度值反而高于原本更亮的像素点。前述测试图各像素点选到的参考值图像见下图（经过了一定缩放以重点突出过亮区域）：
可以看出参考值Vsm在亮区某些地方是突变的。由于尺度采样是高度离散的，这种尺度选择的跳变造成的亮度不连续很难彻底消除，区域边界的光晕就是这一效应的体现之一。好在一般区域的对比度没有太高，所以适当减小尺度间隔可以显著改善这一问题，但是像太阳中心区域附近这样的仅靠有限地减小尺度间隔就不够了。很容易想到的一个解决方案就是人为地抑制亮区对比度，这通过对超出亮度阈值的区域做个简单的线性缩放即可实现。需要注意的是，如果你想看清亮区内部的部分细节的话，简单的阈值截断是不合适的，超出部分做线性缩放通常是个更好的选择。
前述测试图经改进后的算法处理后的结果如下：
可以看出，改进后太阳中心和夕阳在海面的余晖处理后看起来更加真实和令人舒服。然而，这种改进也不是全无代价的。比如下面的两个例子(前面为改进前处理结果，后面为改进后处理结果)：
改进前虽然亮度反转更突出，但是星芒的放射性更加完整，艺术性更强，而改进后反而破坏了这种效果。凡事皆有代价，图像处理亦是如此，完美的算法并不存在，读者必须充分理解并接受这一事实。
好了，今天的讲解就到此为止吧。读者可以参照代码细细体会算法的精髓。