C语言实现栈和队列【数据结构/初阶】
文章目录
- 1. 栈
-
- 1.1 概念
- 1.2 结构
- 1.3 栈的实现
-
- 1.3.1 结构体和数组元素类型定义
- 1.3.2 栈的初始化与销毁
- 1.3.3 判断栈是否为空
- 1.3.4 压栈
- 1.3.5 出栈
- 1.3.6 获取栈顶元素
- 1.3.7 获取栈的元素个数
- 1.3.8 打印
- 2. 队列
-
- 2.1 概念
- 2.2 结构
- 2.3 队列的实现
-
- 2.3.1 链表和队列结构定义
- 2.3.2 队列的初始化与销毁
- 2.3.3 判断队列是否为空
- 2.3.4 入队
- 2.3.5 出队
- 2.3.6 获取队头和队尾的元素
- 2.3.7 获取队列中元素的个数
- *3. 循环队列
-
- 3.1 ****[设计循环队列](https://leetcode-cn.com/problems/design-circular-queue/)****
-
- 3.1.1 队列结构的声明
- 3.1.2 队列初始化与销毁
- 3.1.3 判断队列是否为空
- 3.1.4 判断队列是否已满
- 3.1.5 入队
- 3.1.6 出队
- 3.1.7 取首
- 3.1.8 取尾
1. 栈
1.1 概念
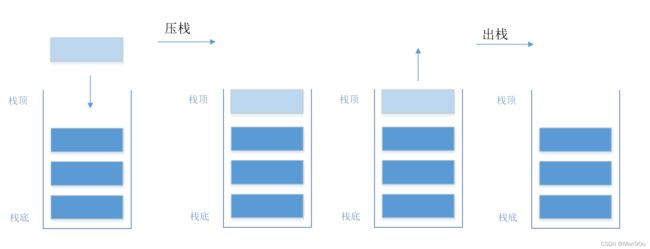
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。**进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。**栈中的数据元素遵守后进先出LIFO的原则。
压栈:栈的插入操作称作进栈/压栈/入栈,
出栈:栈的删除操作称作出栈。
压栈和出栈都在栈顶。
1.2 结构
例如:进栈顺序为1、2、3、4,那么(在进栈时无出栈)出栈时的顺序为4、3、2、1
1.3 栈的实现
栈可以用数组和链表实现。回顾并在此比较两者的优缺点:
- 数组可以通过下标随机访问,但插入删除数据需要挪动数据,但在栈中,这个缺点不会体现出来,因为数据出栈只能在栈顶出,不能在中间出栈。相当于在两端插入或删除数据。
- 链表虽然插入或删除数据不用挪动数据,但这个优点在栈中也不会体现出来。链表的内存不是连续的,CPU高速缓存命中率较低。而且由于链表的结构相较于数组较复杂,每次增加一个节点都要开辟一次内存,(数组一般一次开辟容量的2倍),对性能消耗也是相对较大的。
栈的实现用数组,因为在栈底插入数据的代价较小。
结构:
1.3.1 结构体和数组元素类型定义
结构体成员包含数组,成员数量计数器top(栈顶),容量计数器capacity
typedef int STDataType;
typedef struct Stack
{
STDataType* data;//注意是数组形式
int top;
int capacity;
};
typedef struct Stack Stack;//这是另一种规范的定义写法
1.3.2 栈的初始化与销毁
起初栈需要有空间存放数组元素,capacity不为零,由于还没有元素放入,top为0,要为数组开辟capacity个以结构为大小的空间
//初始化栈
void StackInit(Stack* pst)
{
assert(pst);
pst->data = (STDataType*)malloc(sizeof(STDataType) * 4);
pst->top = 0;
pst->capacity = 4;
}
为避免造成内存泄漏的问题,有内存的开辟就一定要有内存的销毁
- 只要将计数器置零,数组地址置空即可,无需在处理数组中之前存放的元素
//销毁栈
void StackDestroy(Stack* pst)
{
assert(pst);
free(pst->data);
pst->data = NULL;
pst->top = 0;
pst->capacity = 0;
}
1.3.3 判断栈是否为空
巧妙地将top == 0的结果作为返回值,为空则返回true,否则返回false
有些编译器不支持C99,所以bool可以先定义一下
typedef int bool;
bool StackEmpty(Stack* pst)
{
assert(pst);
return pst->top == 0;//top为0则为真,否则为假
}
1.3.4 压栈
压栈的操作就是对数组的尾插
- 注意判断元素个数是否达到容量
- 注意判断达到容量以后开辟内存是否成功
void StackPush(Stack* pst, STDataType x)
{
assert(pst);
//判断top是否达到容量,达到则扩容
if (pst->top == pst->capacity)
{
STDataType* tmp = (Stack*)realloc(pst->data, sizeof(STDataType) * pst->capacity * 2);//扩容
if (tmp == NULL)//增容失败
{
printf("realloc failed\n");
exit(-1);//告诉系统这是异常终止程序
}
pst->data = tmp;
pst->capacity = pst->capacity * 2;//更新容量
}
pst->data[pst->top] = x;//压入数据
pst->top++;
}
1.3.5 出栈
出栈相当于对数组尾删,只需将top往后移一步即可,无需再处理删除的元素
- 注意判断栈是否为空
//出栈(相当于尾删)
void StackPop(Stack* pst)
{
assert(pst);
assert(!StackEmpty(pst));
pst->top--;
}
1.3.6 获取栈顶元素
由于top是从0开始的,所以top指向的是最新元素的下一个位置,要得到栈顶元素,下标要-1
- 注意判断栈是否为空
//获取栈顶元素
STDataType StackTop(Stack* pst)
{
assert(pst);
assert(!StackEmpty(pst));
return pst->data[pst->top - 1];//top指向第一个元素的下一位
}
1.3.7 获取栈的元素个数
top就是元素个数计数器,直接返回它即可
//获取栈的元素个数
int StackSize(Stack* pst)
{
assert(pst);
return pst->top;//top从0开始,其值等于元素个数
}
1.3.8 打印
遍历打印即可
//打印
void StackPrint(Stack* pst)
{
assert(pst);
for (int i = 0; i < pst->top; i++)
{
printf("%d ", pst->data[i]);
}
}
2. 队列
2.1 概念
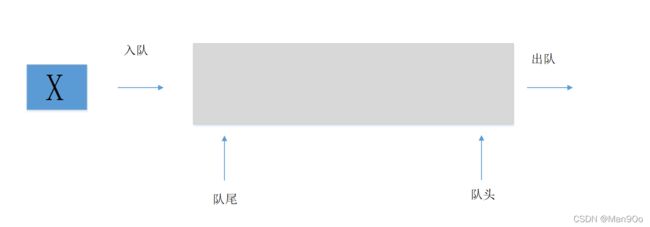
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出的特点
入队列:进行插入操作的一端称为队尾
出队列:进行删除操作的一端称为队头
2.2 结构
2.3 队列的实现
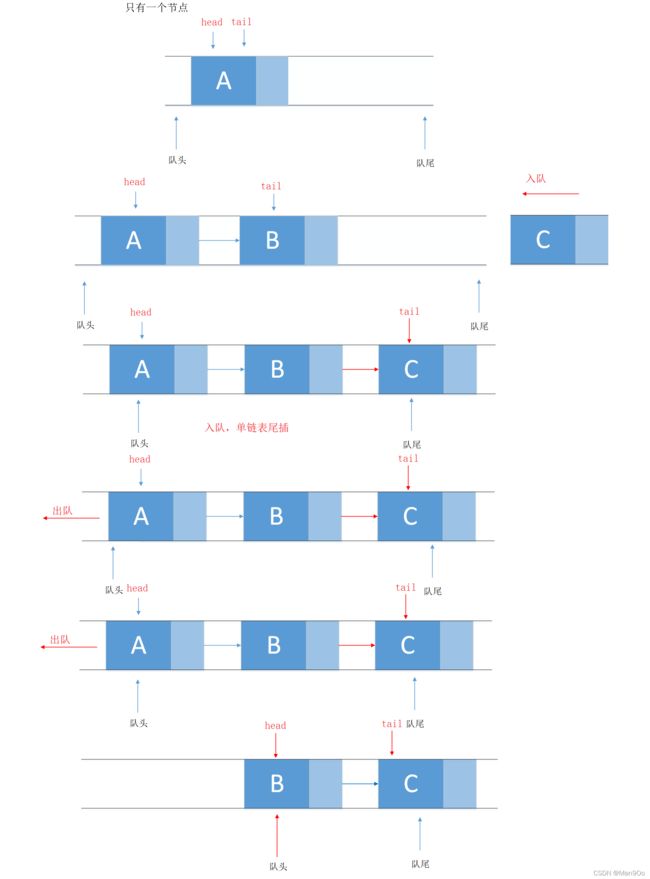
队列的结构决定了它的性质,只能在队尾入,在队头出。所以如果用数组实现队列,就正好体现了它的缺点,每次头删都要重新挪动一次数据。使用链表实现队列能避免这个问题。
使用单向链表实现队列,其实就是对链表的尾增和头删。
结构:
2.3.1 链表和队列结构定义
typedef int QDataType;
//用链表表示队列
typedef struct QueueNode
{
struct QueueNode* next;
QDataType data;
};
typedef struct QueueNode QNode;
//队列结构
typedef struct Queue
{
QNode* head;
QNode* tail;
};
2.3.2 队列的初始化与销毁
初始化时,没有节点,head和tail指向NULL
//初始化
void QueueInit(Queue* pq)
{
//0个元素,头尾指针置空
pq->head = NULL;
pq->tail = NULL;
}
将每个节点销毁,两指针重新指向NULL
void QueueDestroy(Queue* pq)
{
QNode* cur = pq->head;
while (cur)//将每个节点都销毁
{
QNode* next = cur->next;
free(cur);
cur = next;//迭代
}
//头尾指针置空
pq->head = NULL;
pq->tail = NULL;
}
2.3.3 判断队列是否为空
思路同栈
如果编译器支持C99,那么可以引用头文件
#include //判断队列是否为空
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->head == NULL;
}
2.3.4 入队
相当于给单链表尾插
- 注意判断开辟内存是否成功
- 注意判断链表为空
//入队(尾插)
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
//新增节点
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
printf("malloc failed\n");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
if (pq->tail == NULL)//没有元素
{
pq->head = newnode;
pq->tail = newnode;
}
else
{
pq->tail->next = newnode;//链接旧尾和新节点
pq->tail = newnode;//更新尾
}
}
2.3.5 出队
相当于给单链表头删
- 注意判断只有链表为空和只有一个节点的情况
//出队(头删)
void QueuePop(Queue* pq)
{
assert(pq);
assert(pq->head);//判断链表为空
if (pq->head->next == NULL)//只有一个节点
{
free(pq->head);
pq->head = NULL;
pq->tail = NULL;
}
else
{
QNode* next = pq->head->next;//保存头的下一个节点
free(pq->head);
pq->head = next;
}
}
2.3.6 获取队头和队尾的元素
思路同栈
//获取队头的元素
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->head->data;
}
//获取队尾的元素
QDataType QueueBack(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->tail->data;
}
2.3.7 获取队列中元素的个数
迭代计数即可
//获取队列中元素的个数
int QueueSize(Queue* pq)
{
int size = 0;
QNode* cur = pq->head;
while (cur)
{
size++;
cur = cur->next;
}
return size;
}
*3. 循环队列
循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
来源:力扣(LeetCode)
循环队列用数组和链表皆可实现。但实现过程需要注意以下问题。
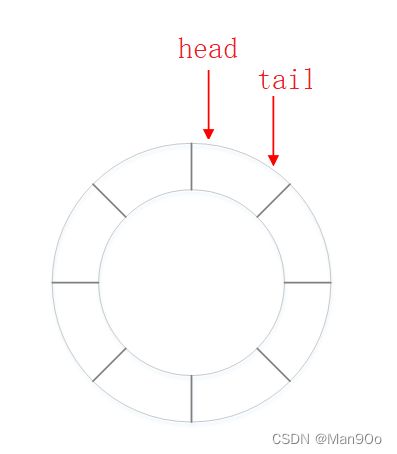
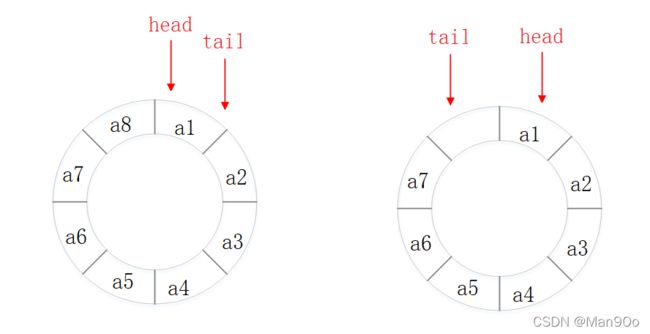
下面将循环队列形象地用环形表示:
head和tail起始都指向第一个元素,tail随着新元素的增加而往下走,直到元素个数达到队列容量。
问题在于:队列全空和队列全满的条件是相同的:head和tail指向同一个位置。
如何解决?
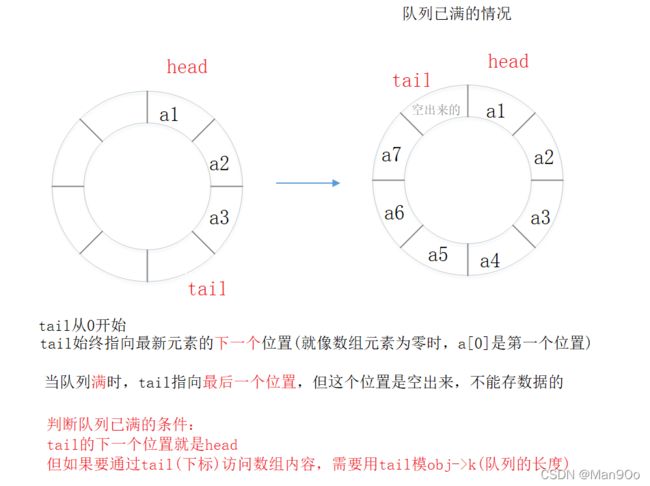
将一个位置空出来,不存储有效数据。
这样就能区分满和空两种情况了。
- 队列全满:tail的下一个是head
- 队列全空:tail和head相等(包括删除的情况)
3.1 设计循环队列
思路:下面通过数组实现循环队列。思路同上,只不过在下标的处理、条件判断有所不同
3.1.1 队列结构的声明
typedef struct {
int* a;//数组
int k;//队列容量
int head;
int tail;
} MyCircularQueue;
3.1.2 队列初始化与销毁
要为队列和队列中的数组开辟空间,注意数组开辟的空间要比给定的k多一个。
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
obj->a = (int*)malloc(sizeof(int) * (k+1));//要空出一个
obj->k = k;
obj->head = 0;
obj->tail = 0;
return obj;
}
销毁内存只需free掉之前开辟的内存即可,注意顺序
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);//注意顺序
free(obj);
}
3.1.3 判断队列是否为空
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->head == obj->tail;
}
3.1.4 判断队列是否已满
bool myCircularQueueIsFull(MyCircularQueue* obj) {
int tailNext = obj->tail+1;
if(tailNext == obj->k+1)
{
tailNext = 0;
}
return obj->head == tailNext;
}
细节处理:对下标的模处理可以转换为让它重新指向第一个元素的位置。
CPU中只有加法器,直接将它移到数组首端比模运算效率更高。
3.1.5 入队
- 注意判断队列是否已满
- 注意判断tail是否已经指向了最后一个空出来的位置
- 注意计数器的迭代
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if(myCircularQueueIsFull(obj))//满了
{
return false;
}
else
{
obj->a[obj->tail] = value;
obj->tail++;
if(obj->tail == obj->k+1)
{
obj->tail = 0;
}
return true;
}
}
3.1.6 出队
- 注意判断队列是否为空
- 注意判断tail是否已经指向了最后一个空出来的位置
- 注意计数器的迭代
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))//空了
{
return false;
}
else
{
obj->head++;
if(obj->head == obj->k+1)//tail已经指向了最后一个空出来的位置
{
obj->head = 0;
}
return true;
}
}
3.1.7 取首
- 注意判断队列是否为空
int myCircularQueueFront(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
else
{
return obj->a[obj->head];
}
}
3.1.8 取尾
- 注意判断队列是否为空
- 注意判断tail是否已经指向了最后一个空出来的位置(最新的元素是否是最后一个第k个)
int myCircularQueueRear(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
else
{
int tailPrev = obj->tail - 1;//取最新的有效数据(tail指向它的下一个位置)
if(tailPrev == -1)//说明最新的元素在第k个
{
tailPrev = obj->k;
}
return obj->a[tailPrev];
}
}
日志
4/22/2022
4/22/2022
//修正了内存开辟部分变量的类型