机器学习实战-14利用SVD简化数据-改进推荐系统
虽然本章标题是SVD,但是感觉本章的内容核心却有点像是推荐系统,SVD的主要作用优化数据,简化运算。对于推荐系统,生活中处处都是,比如火热的网易云音乐,其中就是用到的因子推荐算法,记得我的第一篇博客就是从知乎上转载下来的;另外还有今日头条;其他的应用其实也有,但是自我感觉,这两个应用应该是最好的。记得最近俱乐部有一个网络订餐推荐系统的项目,而这正是书中所举的例子,作为一个推荐系统,其实饮食推荐系统和音乐推荐有很多类似或者可能完全相同处理。它的基本逻辑就是找和你经常吃同样美食的用户A,然后给你推荐用户A吃过的,而你却没吃的。比如你和A,你们都喜欢吃川菜,但是A吃过夫妻肺片,并且对其评价很好,而你没吃过,这时候,推荐系统通过计算就很可能给你推荐夫妻肺片。
由于吴军《数学之美》中对此解释非常好,所以这里转载:
“三个矩阵有非常清楚的物理含义。第一个矩阵X中的每一行表示意思相关的一类词,其中的每个非零元素表示这类词中每个词的重要性(或者说相关性),数值越大越相关。最后一个矩阵Y中的每一列表示同一主题一类文章,其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵则表示类词和文章雷之间的相关性。因此,我们只要对关联矩阵A进行一次奇异值分解,w 我们就可以同时完成了近义词分类和文章的分类。(同时得到每类文章和每类词的相关性)。”
一、SVD的应用
优点:简化数据、去除噪声、提高算法效果
缺点:逻辑转换可能难以理解
使用类型:数值型数据
隐性语义索引LSI(信息检索)
这里,我谈谈我的理解,可能不太准确。首先我们谈谈一般搜索的两个问题:- 关键词写错。比如我搜索“北晶”,我的本意是搜索“北京”,但是搜索引擎还是会给我推荐“北京”的结果。为什么?如果是简单的搜索,搜索引擎将查找所有与“北晶”相关的信息,而忽视“北京”。但是通过SVD,可以将“北京”“背景”“背静”等相似拼音的词语归为一个集合,这样,当搜索不存在是就会判断是否输入错误,已在集合里面查找相关的词语。
- 同义词搜索。比如我们搜索“SVD”,尽管SVD和PCA可能存在许多的差别,但是在系统内部,由于使用SVD对所有的文章进行处理后发现,SVD和PCA经常一起出现在一篇文章中,因此将这两个次聚为一类,这时当我们搜索“SVD”时,其实,也会给我门提供PCA的信息。
上面就是SVD对搜索引擎的改进
推荐系统
在前言中,通过餐厅个性化订餐系统讲述了SVD的应用,其实,这是和信息检索一个道理,就是找到和你口味相同的所有用户,推荐他们吃过,而你没吃过的食物。
二、矩阵分解和推导
SVD也是对矩阵进行分解,但是和特征分解不同,SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵,那么我们定义矩阵A的SVD为:
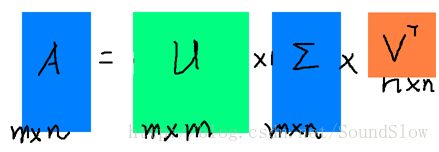
其中U是一个m×m的矩阵,Σ是一个m×n的矩阵,除了主对角线上的元素以外全为0,主对角线上的每个元素都称为奇异值,V是一个n×n的矩阵。U和V都是酉矩阵,即满足UTU=I,VTV=I。下图可以很形象的看出上面SVD的定义:

具体的数学逻辑推导参考:知乎
三、SVD实际应用案例
接下来是通过SVD来优化推荐系统,以及压缩图像
首先梳理几个点:
* 1.原始推荐系统如何推荐:一般推家系统都是通过计算两个用户的相似度,来进行更推荐
* 2.相似度的计算:(最后都要归一化到0-1)
* 欧式距离
* 余弦相似度
* 皮尔逊相关系数

* 3.改进推荐系统:原始的推荐系统需要大量的计算,通过使用SVD简化数据,能够大大加快运算的速度
* 4.重构矩阵:即尽可能的保留原始矩阵的信息
* 我们可以发现得到的特征值,前3个比其他的值大很多,所以可以将最后2个值去掉,因为他们的影响很小。
![]()

![]()
* 上面例子就可以将原始数据用如下结果近似:
![]()
四、推荐系统和图像压缩案例1、2
- 代码svdRec.py
"""
@author: zoutai
@file: svdRec.py
@time: 2017/11/17
@description:
"""
from numpy import *
def loadExData():
return[[1, 1, 1, 0, 0],
[2, 2, 2, 0, 0],
[1, 1, 1, 0, 0],
[5, 5, 5, 0, 0],
[1, 1, 0, 2, 2],
[0, 0, 0, 3, 3],
[0, 0, 0, 1, 1],]
def loadExData2():
return[[2, 0, 0, 4, 4, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 4, 0],
[3, 3, 4, 0, 3, 0, 0, 2, 2, 0, 0],
[5, 5, 5, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 5, 0, 0, 5, 0],
[4, 0, 4, 0, 0, 0, 0, 0, 0, 0, 5],
[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 4],
[0, 0, 0, 0, 0, 0, 5, 0, 0, 5, 0],
[0, 0, 0, 3, 0, 0, 0, 0, 4, 5, 0],
[1, 1, 2, 1, 1, 2, 1, 0, 4, 5, 0]]
def loadExData3():
return[
[4, 4, 0, 2, 2],
[4, 0, 0, 3, 3],
[4, 0, 0, 1, 1],
[1, 1, 1, 2, 0],
[2, 2, 2, 0, 0],
[1, 1, 1, 0, 0],
[5, 5, 5, 0, 0]]
# 三个相似度计算函数:欧氏距离、余弦函数、皮尔逊相关系数
# 量度在0-1之间,0表示相似度最小,反之越大
def eulidSim(inA,inB):
return 1.0/(1.0 + linalg.norm(inA,inB))
def cosSim(inA,inB):
num = float(inA.T*inB) # 分子Numerator,分母denominator
denom = linalg.norm(inA)*linalg.norm(inB)
return 0.5+0.5*(num/denom)
# 这个内部逻辑不是很清楚
def pearsSim(inA,inB):
if len(inA) < 3:
return 1.0
return 0.5 + 0.5 * corrcoef(inA,inB,rowvar=0)[0][9]
#第一个推荐引擎,不使用SVD,单纯的相似度计算公式来衡量
# standEst对没有进行评分的物品,进行评分的策略
def standEst(dataMat,user,simMeas,item):
n = shape(dataMat)[1]
simTotal = 0.0; rateSimTotal = 0.0
for j in range(n):
userRating = dataMat[user,j]
if userRating == 0:
continue
# 寻找对Item和j项商品都进行评分了的所有用户ID
overLap = nonzero(logical_and(dataMat[:,item].A > 0,dataMat[:,j].A > 0))[0]
if len(overLap) == 0:
similarity = 0.0
else:
similarity = simMeas(dataMat[overLap,item],dataMat[overLap,j])
simTotal += similarity
rateSimTotal += similarity * userRating
if simTotal == 0:
return 0
else:
return rateSimTotal/simTotal
# estMethod=standEst:传递一个函数
def recommend(dataMat,user,N=3,sigMeas=cosSim,estMethod=standEst):
unratedItems = nonzero(dataMat[user,:].A==0)[1] # 查找当前user的未评级商品id
if len(unratedItems) == 0:
print("you rate allItems")
itemScores = []
for item in unratedItems:
iScore = estMethod(dataMat,user,sigMeas,item)
itemScores.append((item,iScore))
# 寻找前N项商品,逆序排序;
# 疑问:这个jj啥意思?我想应该是:
# jj[1]取的是分数,即按分数来进行排序,取分数最高的N项
return sorted(itemScores,key=lambda jj:jj[1],reverse=True)[:N]
# 基于SVD的评分估计-取代standEst
def svdEst(dataMat,user,simMeas,item):
n = shape(dataMat)[1]
simTotal = 0.0; rateSimTotal = 0.0
# 进行奇异值SVD分解
U,sigma,VT = linalg.svd(dataMat)
sigma4 = mat(eye(4)*sigma[:4])
for j in range(n):
userRating = dataMat[user,j]
if userRating == 0 or j == item:
continue
# 寻找对Item和j项商品都进行评分了的所有用户ID
similarity = simMeas(dataMat[item,].T,dataMat[j,].T)
simTotal += similarity
rateSimTotal += similarity * userRating
if simTotal == 0:
return 0
else:
return rateSimTotal/simTotal
def printMat(inMat,thresh=0.8):
for i in range(32):
for k in range(32):
if float(inMat[i,k]) > thresh:
print(1)
else:
print(0)
print('')
# 其实就是一个分解在组合的过程
def imgCompress(numSV=3,thresh=0.8):
myl = []
for line in open('0_5.txt').readlines():
newLine = []
for i in range(32):
newLine.append(int(line[i]))
myl.append(newLine)
myMat = mat(myl)
print("原始矩阵:")
print(myMat,thresh)
U,sigma,VT = linalg.svd(myMat)
SigRecon = mat(zeros((numSV,numSV)))
for k in range(numSV):
SigRecon[k,k] = sigma[k]
reconMat = U[:,:numSV]*SigRecon*VT[:numSV,:]
print("压缩后")
printMat(reconMat,thresh)- 测试代码:test.py
"""
@author: zoutai
@file: test.py
@time: 2017/11/17
@description:
"""
from numpy import *
from unit14.svdRec import *
set_printoptions(suppress=True) # 设置numpy不以科学计数法输出,即e
# tets1
U,sigma,VT = linalg.svd([[1,1],[7,7]])
#print(U,sigma,VT)
# test2
U,sigma,VT = linalg.svd(loadExData())
# 对角矩阵,但是写成一维数组的形式;[ 9.64365076e+00 5.29150262e+00 7.40623935e-16 4.05103551e-16 2.21838243e-32]
print(sigma) # 通过观察sigma发现,前三项远大于后面几项,所以取前三项就能代表所有项
# 重构对角矩阵(前三项)
sigma3 = mat([[sigma[0],0,0],[0,sigma[1],0],[0,0,sigma[2]]])
# 还原数据
newDataMat = U[:,:3] * sigma3 * VT[:3,:]
print(array(newDataMat))
# test3-餐厅菜肴推荐----result:[(2, 2.5), (1, 2.0243290220056256)]
# 再次提醒自己:数据格式,mat,array等的区别,用法
recommendItems = recommend(mat(loadExData3()),2)
print("为第2个用户推荐菜单是:",recommendItems)
# test4-利用SVD提高优化效果----result:[(3, 3.2440521369249682), (10, 3.1576182912586654), (8, 3.1428571428571428)]
recommendItems4 = recommend(mat(loadExData2()),2,estMethod=svdEst)
print("为第2个用户推荐菜单是:",recommendItems4)
# 这个此时对不上号,可能存在错误
# 基于SVD的图像压缩
imgCompress()最后、补充内容
- 推荐引擎的检验:检查检验、最小均方根误差
- 推荐系统其他的改进
- 大规模数据,SVD会降低程序的速度,SVD可以在调入时运行一次。之后每天运行一次或者频率更低。不需要频繁运行。并且需要离线运行
- 节约存储空间:通过观察,我们发现,上面的矩阵存在很多的0值,所以可以不保存这些值,节约内存和计算开销
- 另外相似度得分不需要每次都计算:可以离线保存相似度得分。另外计算时,物品之间的相似度不同的用户是一样的可以复用
- 冷启动(面试):即对于一个新用户或者新的商品,如何推荐?没有相关数据
- 可以首次推荐当做搜索问题来处理,用户主动搜索才会出现
- 对于图像压缩:如果理解SVD的数学公式推导,就不难理解,其实,就是将像素在坐标轴上进行压缩。比如高中,我们学数学向量坐标时,经常做的作业就是平移压缩扩大,比函数y=f(x),横坐标缩小两倍就是:y=f(2x)
参考链接